Article contents
Are planetary dynamos driven by helical waves?
Published online by Cambridge University Press: 01 June 2018
Abstract
In most numerical simulations of the Earth’s core the dynamo is located outside the tangent cylinder and, in a zero-order sense, takes the form of a classical 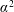 $\unicode[STIX]{x1D6FC}^{2}$ dynamo. Such a dynamo usually requires a distribution of helicity,
$\unicode[STIX]{x1D6FC}^{2}$ dynamo. Such a dynamo usually requires a distribution of helicity, 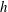 $h$, which is asymmetric about the equator and in the simulations it is observed that, outside the tangent cylinder, the helicity is predominantly negative in the north and positive in the south. If we are to extrapolate the results of these simulations to the planets, we must understand how this asymmetry in helicity is established and ask if the same mechanism is likely to operate in a planet. In some of the early numerical dynamos, which were too viscous by a factor of at least
$h$, which is asymmetric about the equator and in the simulations it is observed that, outside the tangent cylinder, the helicity is predominantly negative in the north and positive in the south. If we are to extrapolate the results of these simulations to the planets, we must understand how this asymmetry in helicity is established and ask if the same mechanism is likely to operate in a planet. In some of the early numerical dynamos, which were too viscous by a factor of at least 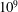 $10^{9}$, as measured by the Ekman number, the asymmetric helicity distribution was attributed to Ekman pumping. However, Ekman pumping plays much less of a role in more recent, and less viscous, numerical dynamos, and almost certainly plays no significant role in the core of a planet. So the question remains: what establishes the asymmetric helicity distribution in the simulations and is this mechanism likely to carry over to planetary cores? In this paper we review the evidence that planetary dynamos, and their numerical analogues, might be maintained by helical waves, especially inertial waves, excited in and around the equatorial regions. This cartoon arises from the observation that there tends to be a statistical bias in the buoyancy flux towards the equatorial regions, and so waves are preferentially excited there. Moreover, upward (downward) propagating inertial waves carry negative (positive) helicity, which leads naturally to a segregation in
$10^{9}$, as measured by the Ekman number, the asymmetric helicity distribution was attributed to Ekman pumping. However, Ekman pumping plays much less of a role in more recent, and less viscous, numerical dynamos, and almost certainly plays no significant role in the core of a planet. So the question remains: what establishes the asymmetric helicity distribution in the simulations and is this mechanism likely to carry over to planetary cores? In this paper we review the evidence that planetary dynamos, and their numerical analogues, might be maintained by helical waves, especially inertial waves, excited in and around the equatorial regions. This cartoon arises from the observation that there tends to be a statistical bias in the buoyancy flux towards the equatorial regions, and so waves are preferentially excited there. Moreover, upward (downward) propagating inertial waves carry negative (positive) helicity, which leads naturally to a segregation in 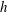 $h$.
$h$.
Keywords
- Type
- Review
- Information
- Copyright
- © Cambridge University Press 2018
References
- 9
- Cited by


