Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-18T05:39:47.119Z Has data issue: false hasContentIssue false
  • English
  • Français

Analysis of the isotropic and anisotropic Grad–Shafranov equation

Part of: Focus on Fusion

Published online by Cambridge University Press:  28 September 2021

S. Jeyakumar Open the ORCID record for S. Jeyakumar [Opens in a new window] ,
D. Pfefferlé Open the ORCID record for D. Pfefferlé [Opens in a new window] ,
M.J. Hole Open the ORCID record for M.J. Hole [Opens in a new window]  and
Z.S. Qu
S. Jeyakumar*
Affiliation:
Mathematical Sciences Institute, Australian National University, Acton, ACT 2601, Australia The University of Western Australia, 35 Stirling Highway, Crawley, WA 6009, Australia
D. Pfefferlé
Affiliation:
The University of Western Australia, 35 Stirling Highway, Crawley, WA 6009, Australia
M.J. Hole
Affiliation:
Mathematical Sciences Institute, Australian National University, Acton, ACT 2601, Australia Australian Nuclear Science and Technology Organisation, Locked Bag 2001, Kirrawee DC, NSW 2232, Australia
Z.S. Qu
Affiliation:
Mathematical Sciences Institute, Australian National University, Acton, ACT 2601, Australia
*
†Email address for correspondence: sandra.jeyakumar@anu.edu.au
Get access Rights & Permissions [Opens in a new window]

Abstract

Pressure anisotropy is a commonly observed phenomenon in tokamak plasmas, due to external heating methods such as neutral beam injection and ion-cyclotron resonance heating. Equilibrium models for tokamaks are constructed by solving the Grad–Shafranov equation; such models, however, do not account for pressure anisotropy since ideal magnetohydrodynamics assumes a scalar pressure. A modified Grad–Shafranov equation can be derived to include anisotropic pressure and toroidal flow by including drift-kinetic effects from the guiding-centre model of particle motion. In this work, we have studied the mathematical well-posedness of these two problems by showing the existence and uniqueness of solutions to the Grad–Shafranov equation both in the standard isotropic case and when including pressure anisotropy and toroidal flow. A new fixed-point approach is used to show the existence of solutions in the Sobolev space $H_0^1$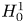 to the Grad–Shafranov equation, and sufficient criteria for their uniqueness are derived. The conditions required for the existence of solutions to the modified Grad–Shafranov equation are also constructed.

Keywords

fusion plasmaplasma heating
Type
Research Article
Information
Journal of Plasma Physics , Volume 87 , Issue 5 , October 2021 , 905870506
Check for updates
Copyright
Copyright © The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Adams, R.A. & Fournier, J.J.F. 1975 Sobolev Spaces, 3rd edn. Elsevier Science.Google Scholar
Beliën, A.J.C., Botchev, M.A., Goedbloed, J.P., van der Holst, B. & Keppens, R. 2002 FINESSE: axisymmetric MHD equilibria with flow. J. Comput. Phys. 182 (1), 91–117.CrossRefGoogle Scholar
Brezis, H. 2010 Functional Analysis, Sobolev Spaces and Partial Differential Equations. Springer.CrossRefGoogle Scholar
Chew, G.F., Goldberger, M.L. & Low, F.E. 1956 The Boltzmann equation and the one-fluid hydromagnetic equations in the absence of particle collisions. Proc. R. Soc. A 236, 112–118.Google Scholar
Dobrott, D. & Greene, J.M. 1970 Steady flow in the axially symmetric torus using the guiding-center equations. Phys. Fluids 13, 2391–2397.CrossRefGoogle Scholar
Evans, L.C. 2010 Partial Differential Equations, 2nd edn. American Mathematical Society.Google Scholar
Fitzgerald, M., Appel, L.C. & Hole, M.J. 2013 EFIT tokamak equilibria with toroidal flow and anisotropic pressure using the two-temperature guiding-centre plasma. Nucl. Fusion 53, 113040.CrossRefGoogle Scholar
Freidberg, J.P. 1982 Ideal magnetohydrodynamic theory of magnetic fusion systems. Rev. Mod. Phys. 54, 801–902.CrossRefGoogle Scholar
Fujii, N. & Hirai, M. 1983 On the existence of a free boundary solution of the Grad-Shafranov equation. J. Plasma Phys. 30, 255–266.CrossRefGoogle Scholar
Gilbarg, D. & Trudinger, N.S. 1998 Elliptic Partial Differential Equations of Second Order, 3rd edn. Springer.Google Scholar
Gorelenkov, N.N. & Zakharov, L.E. 2018 Plasma equilibrium with fast ion orbit width, pressure anisotropy, and toroidal flow effects. Nucl. Fusion 58, 082031.CrossRefGoogle Scholar
Grad, H. 1967 Toroidal containment of a plasma. Phys. Fluids 10, 137–154.CrossRefGoogle Scholar
Grad, H. & Rubin, H. 1958 Hydromagnetic equilibria and force-free fields. In Proceedings of the Second United Nations International Conference on the Peaceful Uses of Atomic Energy, vol. 31. pp. 190–197. United Nations Publication.Google Scholar
Guazzotto, L. & Hameiri, E. 2014 A model for transonic plasma flow. Phys. Plasmas 21.CrossRefGoogle Scholar
Hole, M.J., von Nessi, G., Fitzgerald, M., McClements, K.G. & Svensson, J. 2011 Identifying the impact of rotation, anisotropy, and energetic particle physics in tokamaks. Plasma Phys. Control. Fusion 53 (7), 074021.CrossRefGoogle Scholar
Iacono, R., Bondeson, A., Troyon, F. & Gruber, R. 1990 Axisymmetric toroidal equilibrium with flow and anisotropic pressure. Phys. Fluids B 2, 1794–1803.CrossRefGoogle Scholar
Ivanov, A.A., Martynov, A.A., Medvedev, S.Y. & Poshekhonov, Y.Y. 2015 Tokamak plasma equilibrium problems with anisotropic pressure and rotation and their numerical solution. Plasma Phys. Rep. 41, 203–211.CrossRefGoogle Scholar
Lax, P.D. & Milgram, A.N. 1954 Contributions to the Theory of Partial Differential Equations. Princeton University Press.Google Scholar
Pataki, A., Cerfon, A.J., Freidberg, J.P., Greengard, L. & O'Neil, M. 2013 A fast, high-order solver for the Grad–Shafranov equation. J. Comput. Phys. 243, 28–45.CrossRefGoogle Scholar
Qu, Z.S., Fitzgerald, M. & Hole, M.J. 2014 Analysing the impact of anisotropy pressure on tokamak equilibria. Plasma Phys. Control. Fusion 56, 075007.CrossRefGoogle Scholar
Rupflin, M. 2017 Fixed Point Methods for Nonlinear PDEs. University of Oxford, https://courses.maths.ox.ac.uk/node/165/materials.Google Scholar
Shafranov, V.D. 1963 Equilibrium of a toroidal plasma in a magnetic field. J. Nucl. Energy C 5 (4), 251–258.CrossRefGoogle Scholar
Zwingmann, W., Eriksson, L.-G. & Stubberfield, P. 2001 Equilibrium analysis of tokamak discharges with anisotropic pressure. Plasma Phys. Control. Fusion 43 (11), 1441–1456.CrossRefGoogle Scholar