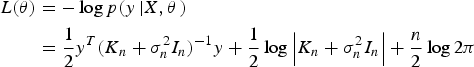1. INTRODUCTION
The navigation system provides navigation data, such as position, velocity and attitude information, which is delivered to a computer for guidance and control (Oh et al., Reference Oh, Hwang, Park, Lee and Kim2005). Whether the navigation data is correct can affect the realization of accurate navigation. In order to improve the reliability and continuity of navigation, integrated navigation is used in many vehicles (Park et al., Reference Park, Jeong, Kim, Hwang and Lee2011). Since several sensors are used in an integrated navigation system, the correctness of sensor measurements directly affects the accuracy of navigation. Once a sensor fails, each subsystem will be contaminated by the fault after the multi-sensor information fusion and feedback. Therefore fault detection is essential to enhance the integrated navigation system's reliability and safety.
Due to the importance of fault detection, many researchers have devoted themselves to improving the reliability of systems. The existing fault detection methods can be broadly classified into three categories (Zhu and Hu, Reference Zhu and Hu2012): fault detection method based on an analytical model, fault detection method based on signal processing and fault detection method based on prior knowledge. Fault detection methods based on an analytical model process and diagnose the information under the assumption that the mathematic model of the system is known. Kalman filtering (Brumback and Srinath, Reference Brumback and Srinath1987; Villez et al., Reference Villez, Srinivasan and Rengaswamy2011) and strong tracking filtering (Wang et al., Reference Wang, Zhou and Jin2004) are the most popular methods in this category. The filter is used to obtain the state estimation for fault prediction based on the analytical model of the system. If the predicted state is greater than the predefined threshold, a fault occurs. Brumback and Srinath (Reference Brumback and Srinath1987) constructed a chi-squared test statistic from the difference between two estimates based on a Kalman filter to realise real-time fault detection. On this basis, Joerger and Pervan (Reference Joerger and Pervan2013) put forward an improved method that can evaluate the probability that an undetected fault causes state estimate errors to exceed predefined bounds of acceptability. However, for some complex nonlinear systems, accurate models cannot be obtained. The other two categories of fault detection methods avoid this problem. Wavelet transformation (Jiang et al., Reference Jiang, Fan and Chen2003; Yan et al., Reference Yan, Gao and Chen2014; Youssef, Reference Youssef2002) and Auto-Regressive Moving Average (ARMA) (Pham and Yang, Reference Pham and Yang2010; Mohsen and Abu EI-Yazeed, Reference Mohsen and Abu EI-Yazeed2004; Munoz, Reference Munoz2000) analyse the measured signal directly, and lead to fault detection methods based on signal processing. These methods detect the fault by extracting characteristic values from the signals such as variance, amplitude and frequency. Fault detection methods based on prior knowledge (Bacha et al., Reference Bacha, Henao, Gossa and Capolino2008; Mahadevan and Shah, Reference Mahadevan and Shah2009; Shabanian and Montazeri, Reference Shabanian and Montazeri2011) have been drawing more and more attention because of their high intelligence. Bacha et al. (Reference Bacha, Henao, Gossa and Capolino2008) realised automatic classification and fault severity degree evaluation by using a Neural Network (NN), of which the inputs were obtained using experimental data related to healthy and faulty machines. However, the dataset needed to train the NN is exceedingly large, which restricts the use of NN in practical application. By contrast, Support Vector Machine (SVM) is a novel learning method that requires only a small number of samples. Mahadevan and Shah (Reference Mahadevan and Shah2009) used a feature selection and identified variables most closely related to the classification of normal and faulty data based on SVM. The outputs of SVM do not have probabilistic meaning. Fortunately, the newly developed Gaussian Process Regression (GPR) can overcome this drawback. It can provide not only the prediction corresponding to the unknown input but also the variance of the prediction (Huber, Reference Huber2014). GPR has many advantages in solving problems in which the dataset has a high dimension or the size of the dataset is relatively small or the samples nonlinear.
This paper proposes a novel fault detection method for an integrated navigation system based on GPR. The Fault Detection Function (FDF), which is composed of the predicted innovation, the actual innovation of the Kalman filter and their variance, is presented. The innovative formula of FDF makes it sensitive to the faults, which is especially favourable to the detection of gradual faults. The GPR model, for the first time, is used to predict the innovation of the Kalman filter. In order to avoid local optimisation, particle swarm optimisation is applied to find the optimal values of GPR hyper-parameters. To highlight the advantages of the proposed method over the traditional method, contrast experiments are carried out. The results demonstrate that the proposed method can detect both abrupt faults and gradual faults effectively, which greatly contributes to enhancing the accuracy and reliability of integrated navigation systems.
The paper is organised as follows: Section 2 introduces GPR assisted by particle swarm optimisation; Section 3 presents the fault detection algorithm based on GPR; Section 4 introduces SINS/GPS/Odometer (Strapdown Inertial Navigation System / Global Positioning System / Odometer) fault-tolerant system; Section 5 describes experimental results; and the last section is committed to concluding remarks.
2. GPR ASSISTED BY PARTICLE SWARM OPTIMISATION
GPR was first proposed by Williams and Rasmussen (Reference Williams and Rasmussen1995). It is a machine learning method developed from Bayesian theory and statistical theory. In mathematics, the GPR model is equivalent to many well-known models, such as spline model, Bayesian linear model and large artificial neural network.
A Gaussian Process (GP) is a collection of random variables, any finite number of which has a joint Gaussian distribution. A GP is completely specified by its mean function and covariance function (Williams and Rasmussen, Reference Rasmussen and Williams2006). The mean function m(x) and the covariance function k(x, x') of a real process f(x) are defined respectively as
Then the GP is written as f(x) ~ GP(m(x), k(x, x')).
The noisy version of the model is described as
where x denotes the input vector. f(x) is the true value of function at location x. y is the observation polluted by noise. Assume that the noise ε observes Gaussian distribution: ε ~ N (0, ![]() ${ \sigma} _n^2 $). Then the prior distribution of observation y, the joint prior distribution of observation y and function value f * can be obtained as follows
${ \sigma} _n^2 $). Then the prior distribution of observation y, the joint prior distribution of observation y and function value f * can be obtained as follows
where the covariance matrix K(X, X) = K n = (k ij). The matrix element k ij = k(x i, xj) is used to measure the correlation between x i and x j. In denotes the n-dimensional unit matrix. n is equal to the column number of X. K(X, x *) = K(x *, X)T is the covariance matrix between training set input X and test point x *. k(x *, x*) is the covariance of test point x * itself.
There are several covariance functions, among which square covariance is often used. The square covariance between x i and x j is written as
where M = diag(l 2) is a diagonal matrix whose order is equal to the dimension of x i. l is the scale of the variance. ![]() $\sigma _f^2 $ denotes the variance of the single.
$\sigma _f^2 $ denotes the variance of the single.
Then, the posterior distribution of function value f * can be calculated as follows
where
here ![]() ${\bar f_{\ast}}$ and cov(f *) are predictive mean and variance of function value f * at location x *, respectively.
${\bar f_{\ast}}$ and cov(f *) are predictive mean and variance of function value f * at location x *, respectively.
There are some unknown parameters in Equations (7) and (8). In order to obtain these parameters, we define the hyper-parameter ![]() $\theta = \{ l\comma \sigma _f^2\comma \sigma _n^2 \} $. Finding the optimal values of the hyper-parameter is crucial to train a good prediction model. To overcome the problems of local optimal, Particle Swarm Optimisation (PSO) combined with the maximum likelihood method is proposed to determine the hyper-parameter.
$\theta = \{ l\comma \sigma _f^2\comma \sigma _n^2 \} $. Finding the optimal values of the hyper-parameter is crucial to train a good prediction model. To overcome the problems of local optimal, Particle Swarm Optimisation (PSO) combined with the maximum likelihood method is proposed to determine the hyper-parameter.
Particle swarm optimisation was introduced by Kennedy and Eberhart (Reference Kennedy and Eberhart1995) and modified by Shi and Eberhart (Reference Shi and Eberhart1998). It came from the simulation of foraging behaviour of bird flocks and fish schools. As an evolutionary algorithm to obtain global optimisation, PSO can solve complex problems which are nonlinear or have multiple extremes.
Each particle represents a possible solution of the problem. The value of the objective function at a particle's position is defined as the fitness of the particle. The quality of a particle is measured by its fitness. Every particle remembers its own best position and the best position of its neighbours, which will be used when the particle changes its velocity. The PSO algorithm searches for the optimal solution by the cooperation and competition among individual particles.
Assume there is a swarm composed of N particles in D-dimensional search space. The position of particle i is written as P i = (p i1p i2 …p iD)T and the velocity written as V i = (v i1v i2 … v iD)T, in which i = 1, 2, …, N. The fitness of particle i is denoted as f p(P i). f p(Pbest i) and Pbest i = (pbest i1pbest i2 … pbest iD)T are the personal best fitness and the personal best position of particle i, respectively. f p(Gbest) and Gbest = (gbest 1gbest 2 … gbest D)T are the global best fitness and the global best position of the particle swarm, respectively. At the iteration m, the d-th dimensional velocity component ![]() $v_{id}^m $ and position component
$v_{id}^m $ and position component ![]() $p_{id}^m $ of particle i can be updated according to Equations (9) and (10), respectively.
$p_{id}^m $ of particle i can be updated according to Equations (9) and (10), respectively.
where m is the current iteration number. d = 1, 2, …, D. ![]() $pbest_{id}^m $ and
$pbest_{id}^m $ and ![]() $gbest_d^m $ are the d-th dimensional component of the particle i's personal best position vector and the global best position vector at iteration m, respectively. r 1, r 2 ∈U(0,1) are random values. c 1 is the cognitive learning factor that represents the cognition that a particle has towards its own success. c 2 is the social learning factor that represents information sharing and cooperation between the particles. ω is the inertia weight that decides the impact of the previous velocity on the current velocity (Mahmoodabadi et al., Reference Mahmoodabadi, Bagheri, Nariman-zadeh and Jamali2012).
$gbest_d^m $ are the d-th dimensional component of the particle i's personal best position vector and the global best position vector at iteration m, respectively. r 1, r 2 ∈U(0,1) are random values. c 1 is the cognitive learning factor that represents the cognition that a particle has towards its own success. c 2 is the social learning factor that represents information sharing and cooperation between the particles. ω is the inertia weight that decides the impact of the previous velocity on the current velocity (Mahmoodabadi et al., Reference Mahmoodabadi, Bagheri, Nariman-zadeh and Jamali2012).
Based on the above theories, the algorithm to obtain the optimal values of the hyper-parameter is described as follows.
Step 1 Build the negative log marginal likelihood as
(11) $$\eqalign{ L(\theta ) &= - \log p(y\left \vert {X,\theta} \right.) \cr & = \displaystyle{1 \over 2}{y^T}{({K_n} + \sigma _n^2 {I_n})^{ - 1}}y + \displaystyle{1 \over 2}\log \left \vert {{K_n} + \sigma _n^2 {I_n}} \right \vert + \displaystyle{n \over 2}\log 2\pi} $$
$$\eqalign{ L(\theta ) &= - \log p(y\left \vert {X,\theta} \right.) \cr & = \displaystyle{1 \over 2}{y^T}{({K_n} + \sigma _n^2 {I_n})^{ - 1}}y + \displaystyle{1 \over 2}\log \left \vert {{K_n} + \sigma _n^2 {I_n}} \right \vert + \displaystyle{n \over 2}\log 2\pi} $$Step 2 Get the partial derivative of L(θ) on θ as
(12)where $$\displaystyle{{\partial L(\theta )} \over {\partial \theta}} = \displaystyle{1 \over 2}tr\left( {\left( {({C^{ - 1}}y) \cdot {{({C^{ - 1}}y)}^T} - {C^{ - 1}}} \right) \cdot \displaystyle{{\partial C} \over {\partial \theta}}} \right)$$
$$\displaystyle{{\partial L(\theta )} \over {\partial \theta}} = \displaystyle{1 \over 2}tr\left( {\left( {({C^{ - 1}}y) \cdot {{({C^{ - 1}}y)}^T} - {C^{ - 1}}} \right) \cdot \displaystyle{{\partial C} \over {\partial \theta}}} \right)$$ $C = {K_n} + \sigma _n^2 {I_n}$.
$C = {K_n} + \sigma _n^2 {I_n}$.Step 3 Define the partial derivative as the fitness function of particle swarm optimisation to be minimised.
Step 3·1 Initialise velocities and positions of the particle swarm with random numbers in the search space.
Step 3·2 Calculate the fitness function of each particle.
Step 3·3 Compare each particle's fitness with its personal best fitness. If the current fitness is better, it will be set as the personal best fitness of the particle, and the current position set as the personal best position.
Step 3·4 Compare each particle's personal best fitness with the global best fitness of the particle swarm. If a personal best fitness is better, then set it as the global best fitness, and the position that corresponds to the global best fitness as the global best position.
Step 3·5 Update velocities and positions of the particles according to Equations (9) and (10).
Step 3·6 If the criterion is met, output the global best position as the optimal solution. Otherwise, go to Step 3·2.
The criterion is usually a sufficiently good fitness or a maximum number of iterations. Then the output global best position is just the optimal solution of hyper-parameter θ.
3. FAULT DETECTION ALGORITHM BASED ON GPR
The error model of the system can be expressed as follows
where X k−1 is the error states of the integrated navigation system at time t k−1, and X k the error states at time t k. Φk,k−1 is the state transition matrix between time t k−1 and t k. Wk is a zero mean white noise sequence with covariance Q k.
The measurement equation of the system may be expressed as follows
where Z k is the measurement differences at time t k. Hk is the local filter measurement matrix. V k is the measurement noise vectors with covariance R k. Wk and V k are assumed to be independent.
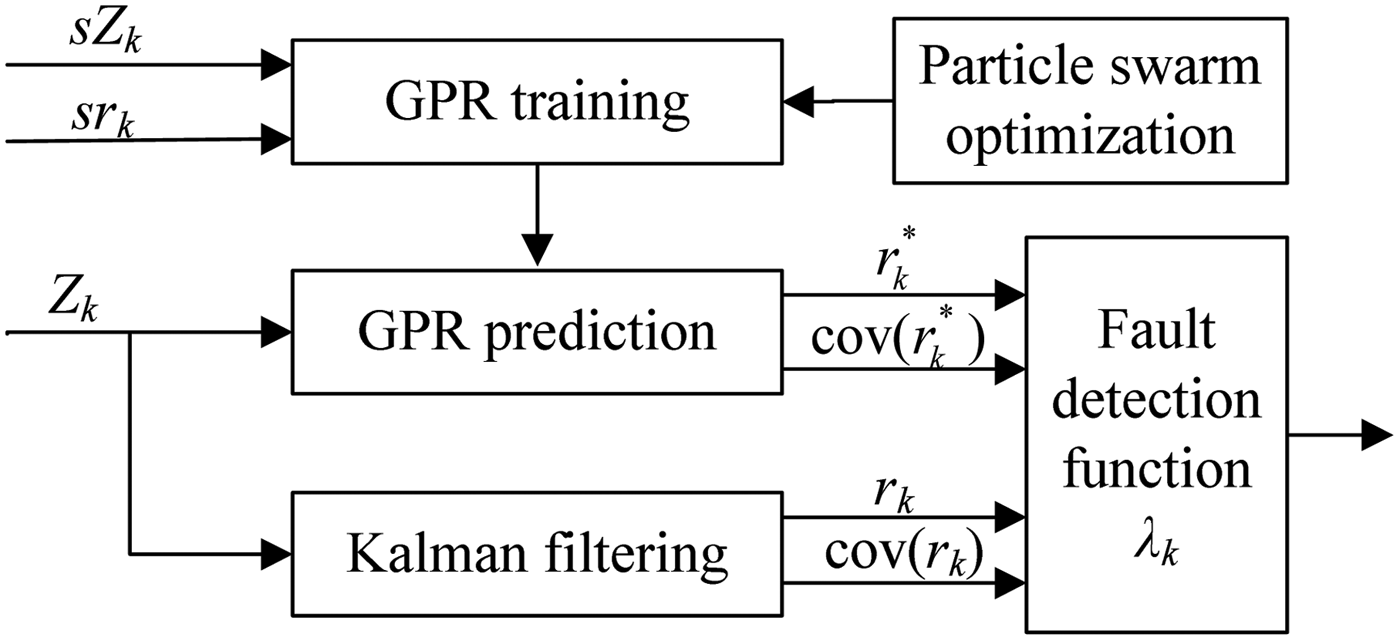
Consider the system described by Equations (13) and (14). The functional diagram of the FDF construction is given in Figure 1. The FDF consists of two parts: the innovation of the Kalman filter and the predicted value of GPR model.

Figure 1. The functional diagram of the FDF construction.
The time update of the Kalman filter defines the new estimate ![]() ${\hat X_{k\comma k - 1}}$ of the state at time t k based on the estimate at the previous time.
${\hat X_{k\comma k - 1}}$ of the state at time t k based on the estimate at the previous time.
where ![]() ${\hat X_{k - 1}}$ is the estimate of the state at time t k−1. Then the estimated measurement of the system can be calculated as follows
${\hat X_{k - 1}}$ is the estimate of the state at time t k−1. Then the estimated measurement of the system can be calculated as follows
The innovation of the Kalman filter is defined as
If there are no failures in the system before time t k−1, the state estimate ![]() ${\hat X_{k - 1}}$ at time t k−1 is correct. In this case,
${\hat X_{k - 1}}$ at time t k−1 is correct. In this case, ![]() ${\hat Z_{k\comma k - 1}}$ represents the estimated measurement of the system with no faults at time t k. As a result, the innovation r k is a Gaussian white sequence with zero mean as the system has no faults between time t k−1 and t k. The covariance of the innovation r k can be calculated as follows
${\hat Z_{k\comma k - 1}}$ represents the estimated measurement of the system with no faults at time t k. As a result, the innovation r k is a Gaussian white sequence with zero mean as the system has no faults between time t k−1 and t k. The covariance of the innovation r k can be calculated as follows
where P k,k −1 denotes the expected value of the covariance matrix at time t k predicted at time t k−1. P k,k −1 can be obtained at the Kalman filter prediction step.
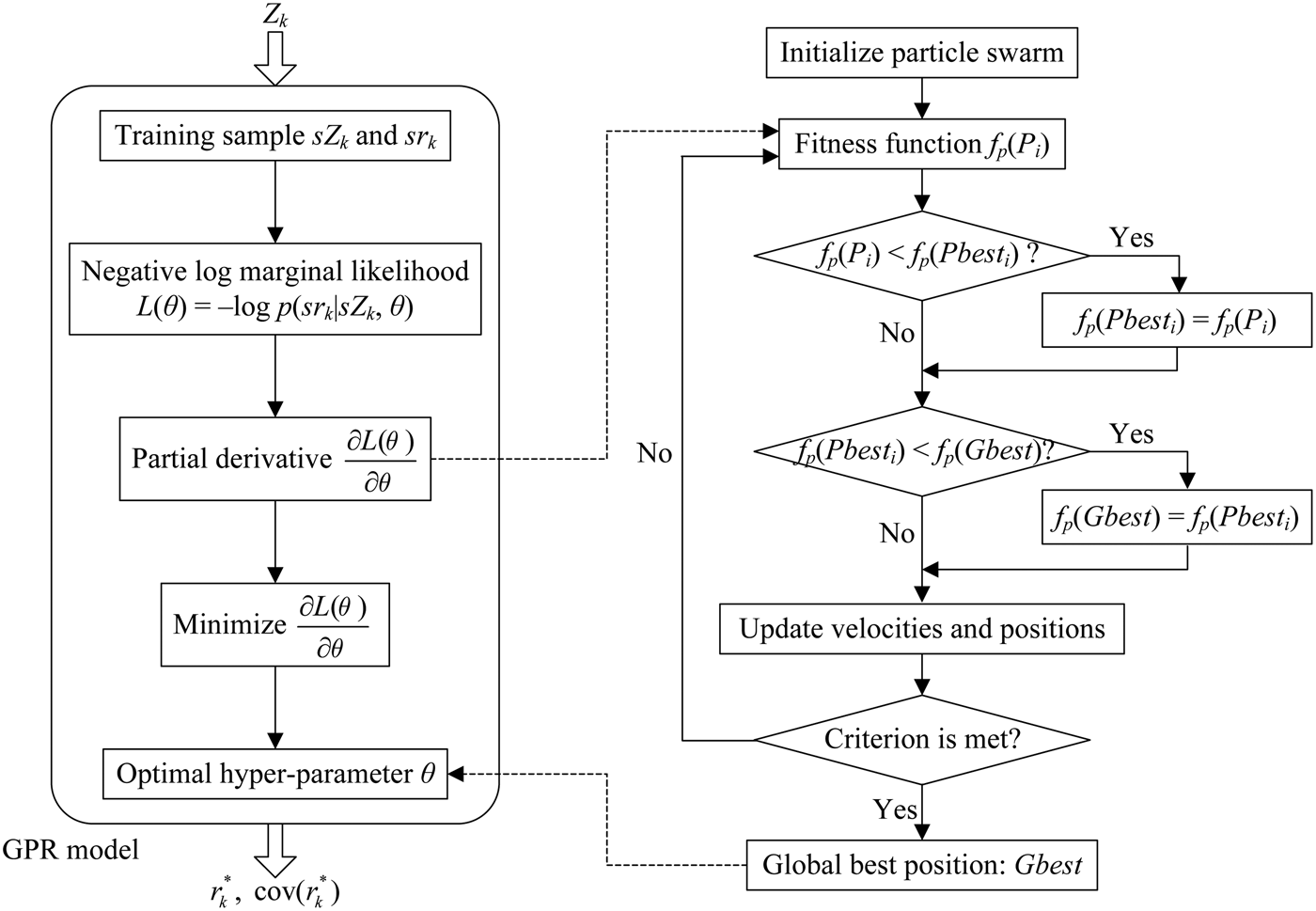
At the same time, a GPR model is devoted to predicting the innovation of the Kalman filter. To build a GPR model, we need to have a dataset as a training sample. Some measurements and its corresponding Kalman filter innovations of the fault-free system, denoted by sZ k and sr k respectively, are taken as the training samples. Using the training samples sZ k and sr k, the GPR model is established through Steps 1–3 listed in Section 2. We train the GPR model based on finding the optimal value of hyper-parameter θ. By defining the partial derivative as the fitness function to be minimised, the PSO algorithm assists in finding the best setting of the GPR hyper-parameter. As the GPR model has been trained, it has the function of prediction. With the measurement Z k as the input, the GPR model can predict the corresponding Kalman filter innovation ![]() $r_k^* $ and give its covariance
$r_k^* $ and give its covariance ![]() ${\mathop{\rm cov}} (r_k^* )$ by Equations (7) and (8) respectively. Figure 2 shows the above description as a flow chart.
${\mathop{\rm cov}} (r_k^* )$ by Equations (7) and (8) respectively. Figure 2 shows the above description as a flow chart.

Figure 2. Particle Swarm Optimisation assists in training the GPR model.
So far, we have got all the elements needed for constituting the FDF. On this foundation, we produce the definition of η k, which is as follows
As the innovation r k and the predicted innovation ![]() $r_k^* $ are independent of each other, the covariance of η k can be obtained as follows
$r_k^* $ are independent of each other, the covariance of η k can be obtained as follows
If the system is operating normally, η k is a Gaussian white sequence with zero mean. If a fault occurs, the mean of η k is no longer equal to zero. Make assumptions about η k as follows:
Hence, there are the following conditional probability density functions:
where |A k| denotes the determinant of A k.
Neyman-Pearson lemma shows the effectiveness of likelihood ratio test. We calculate the log likelihood rate of P r(η|H 1) and P r(η|H 0) as follows
 $$\eqalign{ {\Lambda _k} &= \ln \displaystyle{{{P_r}(\eta \left \vert {{H_1}} \right.)} \over {{P_r}(\eta \left \vert {{H_0}} \right.)}} \cr & = \displaystyle{1 \over 2}[\eta _k^T A_k^{ - 1} {\eta _k} - {({\eta _k} - \mu )^T}A_k^{ - 1} ({\eta _k} - \mu )]} $$
$$\eqalign{ {\Lambda _k} &= \ln \displaystyle{{{P_r}(\eta \left \vert {{H_1}} \right.)} \over {{P_r}(\eta \left \vert {{H_0}} \right.)}} \cr & = \displaystyle{1 \over 2}[\eta _k^T A_k^{ - 1} {\eta _k} - {({\eta _k} - \mu )^T}A_k^{ - 1} ({\eta _k} - \mu )]} $$The log likelihood rate Λk reaches its maximum when μ is equal to η k. Then the FDF can be obtained as follows
 $$\eqalign{ {\lambda _k} &= \eta _k^T A_k^{ - 1} {\eta _k} \cr & = {({r_k} - r_k^* )^T} \cdot {[{\mathop{\rm cov}} ({r_k}) + {\mathop{\rm cov}} (r_k^* )]^{ - 1}} \cdot ({r_k} - r_k^* )} $$
$$\eqalign{ {\lambda _k} &= \eta _k^T A_k^{ - 1} {\eta _k} \cr & = {({r_k} - r_k^* )^T} \cdot {[{\mathop{\rm cov}} ({r_k}) + {\mathop{\rm cov}} (r_k^* )]^{ - 1}} \cdot ({r_k} - r_k^* )} $$As a fault occurs, η k is no longer a Gaussian white sequence with zero mean. The value of FDF λ k will be bigger, which is used to detect the fault. The decision rule is given by the following
where T D is the threshold for detection. If the threshold value is too large, the probability of missed detection will increase. On the other hand, if the threshold value is too small, the probability of false alarm will increase. Therefore, we must measure the probability of false alarm and the probability of missed detection when determining the detection threshold.
4. SINS/GPS/ODOMETER FAULT-TOLERANT SYSTEM
4.1. Fault-tolerant System Structure
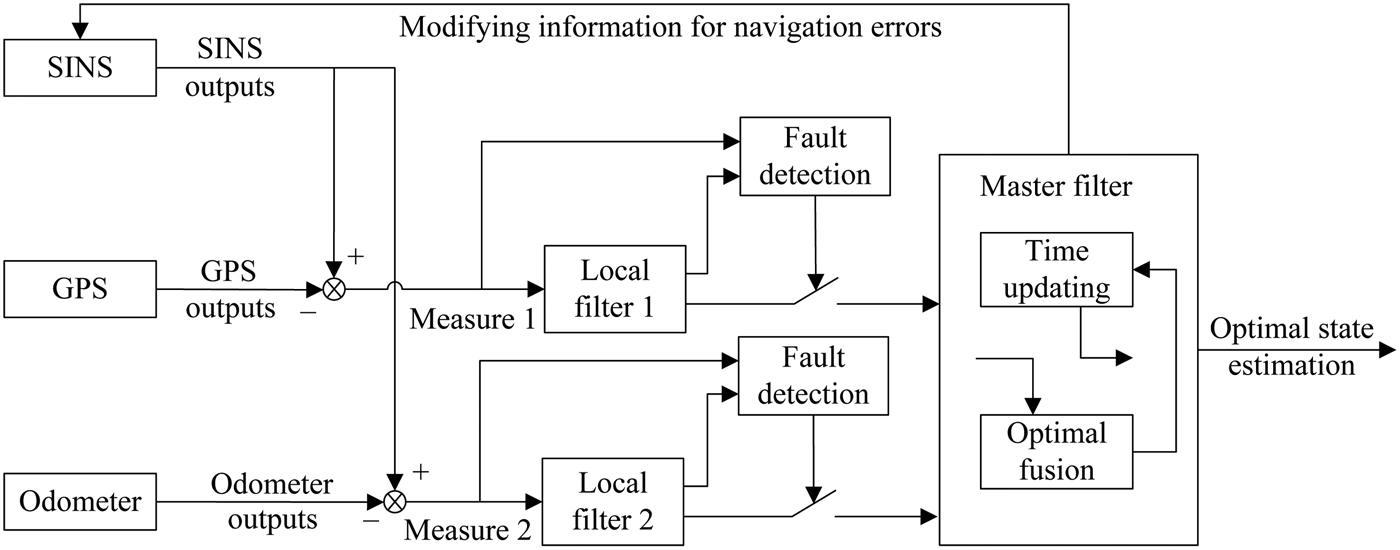
To improve the precision and reliability of the navigation system, multi-navigation system integrated schemes are the most popular at present. The integrated navigation composed of SINS, GPS and odometer is usually applied to land vehicles (Atia et al., Reference Atia, Karamat and Noureldin2014). SINS is an independent navigation system, which provides navigation parameters continually. Since the navigation error of SINS grows over time, assisting navigation approaches are needed to modify the cumulative error. As an assistant navigation observer, the odometer provides the velocity of the vehicle. GPS has high precision of positioning, but its reliability will decline owing to such factors as strong jamming and the blackout effect caused by obstructions.
While a number of methods for multi-sensor integration have been presented for navigation applications, the Kalman filter has proved to have the best performance. Therefore, the Kalman filter is applied to realise the local filter. The fault-tolerant structure of the SINS/GPS/Odometer integrated navigation system is given in Figure 3. SINS is the reference system. Two local filter systems are composed of GPS and odometer assisting SINS, respectively. The fault detection and isolation device is designed respectively for each local filter to detect and expose the subsystem fault in time, ensuring reliability of the navigation system. The FDF of local filter 1 indicates a fault in the GPS receiver, and that of local filter 2 indicates a fault in the odometer. When a fault is detected, the master filter no longer uses the output from the malfunctioning local filter. In other words, if a GPS receiver fault is detected, the SINS/GPS/Odometer integrated navigation system will be changed into a SINS/Odometer one. Similarly, if an odometer fault is detected, the SINS/GPS/Odometer integrated navigation system will be changed into a SINS/GPS one. To ensure the system fault tolerance capability, the non-feedback federal filter is adopted to fuse the information of the subsystems. There is no feedback from the master filter to the local filter, which ensures the best fault tolerance capability. The master filter fuses the fault-free local filter information, and then outputs the optimal state estimation. Navigation error is estimated by the federal filter, and then fed back to the SINS.

Figure 3. SINS/GPS/Odometer fault-tolerant system structure.
4.2. System Model
Set the East-North-Up (ENU) geographic coordinate as the navigation frame (n-frame), and the Right-Front-Up (RFU) frame as the body frame (b-frame). Take the 15-dimensional error state vector as the state variable of the integrated navigation system, namely
where φ e, φn, φu are attitude errors. δV e, δVn, δVu are velocity errors. δL, δλ, δh are position errors. ε x, εy, εz are gyroscope drifts. ▽x, ▽y , ▽z are accelerometer biases.
GPS and odometer assist SINS independently, constituting local filter 1 and local filter 2, respectively. The two local filters estimate the state variable according to the observed data. The measurement equations of the two local filters can be described respectively as
where the subscript SINS, GPS and Od denote SINS output, GPS receiver output and odometer output, respectively. L, λ, V e and V n are latitude, longitude, east velocity and north velocity of the vehicle, respectively. ![]() $X_k^{(1)} = {X_k}$.
$X_k^{(1)} = {X_k}$. ![]() $X_k^{(2)} = {X_k}$.
$X_k^{(2)} = {X_k}$. ![]() $V_k^{(1)} $ and
$V_k^{(1)} $ and ![]() $V_k^{(2)} $ are the measurement noise vectors with covariance
$V_k^{(2)} $ are the measurement noise vectors with covariance ![]() $R_k^{(1)} $ and
$R_k^{(1)} $ and ![]() $R_k^{(2)} $ respectively.
$R_k^{(2)} $ respectively. ![]() $H_k^{(1)} $ and
$H_k^{(1)} $ and ![]() $H_k^{(2)} $ are the local filter measurement matrices which take the following form
$H_k^{(2)} $ are the local filter measurement matrices which take the following form
where I 2×2 is a 2 × 2 identity matrix. 02×6, 02×7, 02×3 and 02×10 are zero matrices with different orders.
Since the non-feedback federal filter is used, the master filter itself has no information distribution and no filtering operation. The only responsibility of the master filter is to fuse the local state estimates. The fusion algorithm can be described as follows
where ![]() $\hat X_k^g $ denotes the optimal estimation.
$\hat X_k^g $ denotes the optimal estimation. ![]() $\hat X_k^{(1)} $ and
$\hat X_k^{(1)} $ and ![]() $\hat X_k^{(2)} $ are the estimates of the error states obtained from local filter 1 and local filter 2, respectively.
$\hat X_k^{(2)} $ are the estimates of the error states obtained from local filter 1 and local filter 2, respectively. ![]() $P_k^{(1)} $ and
$P_k^{(1)} $ and ![]() $P_k^{(2)} $ are the covariance matrixes of
$P_k^{(2)} $ are the covariance matrixes of ![]() $\hat X_k^{(1)} $ and
$\hat X_k^{(1)} $ and ![]() $\hat X_k^{(2)} $, respectively.
$\hat X_k^{(2)} $, respectively. ![]() $P_k^g $ is the covariance matrix of
$P_k^g $ is the covariance matrix of ![]() $\hat X_k^g $.
$\hat X_k^g $.
5. EXPERIMENTS AND RESULTS
To evaluate the proposed detection method, experiments have been carried out. Figure 4 shows the experimental vehicle system that includes IMU, GPS receiver, odometer and navigation computer. Pictures of the IMU and odometer are presented in Figure 5. The reference system is an integrated navigation system consisting of a navigation-grade IMU and a GPS receiver. The reference system provides precise navigation results as reference values. The test navigation system for evaluating the proposed method is composed of a GPS receiver, an odometer and a low-cost IMU. The two systems share the GPS receiver. Field tests were carried out in Beijing in a wide-open area, where satellite signals were easy to receive.

Figure 4. The experimental vehicle system.

Figure 5. IMU and odometer.
To verify the proposed fault detection method, fault information is set artificially by adding a gradual fault, an abrupt fault and an outlier into the measurements of the GPS receiver. A gradual fault is usually caused by increasing measurement noise, small biases or drifts in the signal over time. An abrupt fault may happen when the GPS satellite signals are unavailable for a short time. An outlier is a single point with a large error at a sampling time, which sometimes appears in a GPS receiver. It is worth noting that the simulated fault in the GPS receiver is only added to the measurements of the test navigation system rather than the reference system. The total time of the test was 900 seconds. Fault information is set up as shown in Table 1.
Table 1. Setting faults for GPS receiver.

Based on the above experimental setup, experiments have been performed. Figure 6 shows the position trajectories of the integrated navigation system with different operations. The vehicle travelled from point A to point B. The position trajectory of the system without fault detection has significant errors compared with the reference position trajectory. These large position errors are caused by the added faults in the GPS receiver. When the abrupt fault and the outlier occur, the trajectories of the system with the two methods are pretty close. This reveals that the two methods behave similarly when they deal with the abrupt fault and the outlier. The trajectory of the system with residual chi-squared method deviates from the reference position when the gradual fault occurs. Then as the fault has been detected, the position errors have been reduced gradually. However, under the same experimental conditions, the position curve of the system with the proposed method is almost coincidental with that of the reference system. Thus it can be seen that the proposed method detected all the added faults effectively.

Figure 6. Position trajectories.
To further illustrate the performance of the proposed fault detection method, detailed comparisons have been made between the residual chi-squared test and the proposed method. Figure 7 shows the fault detection function (FDF) of GPS receiver obtained by the residual chi-squared test and the proposed method respectively. FDF reflects the magnitude of fault. The greater the fault, the higher the FDF value will be. A comparison of Figure 7(a) and Figure 7(b) reveals that the FDFs obtained from the two methods are in the same order of magnitude as a fault occurs. However, when there is no fault, the FDFs are on different scales. During the fault-free period, the FDFs of the two methods are mostly in the order of 103 and 10−3 respectively. This shows that the FDF of the proposed method has a more obvious jump in value than that of the residual chi-squared test when a fault occurs.

Figure 7. FDF of GPS receiver. (a) Using residual chi-squared test. (b) Using the proposed method.
The large difference between the FDF value of the fault-free system and that of the failing system benefits the detection of gradual faults. To confirm this point, further comparison and analysis are made. Taking the detection of the gradual fault for the GPS receiver as an example, the FDFs obtained from the two methods are locally amplified, corresponding to Zoom A and Zoom B as shown in Figure 8. Taking the probability of false alarm and missed detection into consideration, the threshold of the residual chi-squared test and that of the proposed method are assigned the values of 5000 and 1 respectively. The threshold of the proposed method is small, thanks to the low FDF value of the fault-free system. Figure 8(a) shows that the FDF value is higher than the predefined threshold starting at the 175th second. So the residual chi-squared test has a delay of 74 s when it is used to detect the gradual fault. As Figure 8(b) shows, the threshold of the proposed method is so small that it is sensitive to the change of FDF value. At time t = 106 s, the FDF value is 1·734 which is greater than the predefined threshold 1. The delay time is 5 s, which is much less than that of the residual chi-squared. Less time delay in detection means lower probability of missed detection. Thus it can be seen that the probability of missed detection of the proposed method has considerably diminished. By comparing Figures 8(a) and 8(b), it is clear that the times of false alarms of the residual chi-squared are significantly more than that of the proposed method. The detailed comparison of detection results is shown in Table 2, which further validates the above analysis.

Figure 8. Drawings of partial enlargement. (a) Zoom A. (b) Zoom B.
Table 2. Comparison of detection results.

Figure 9 shows the position errors obtained by the two methods. In Figure 9(a), the position errors are outside the normal range from the moment that the gradual fault is added to the measurements of the GPS receiver. The reason for this phenomenon is that the gradual fault is not detected until the time t = 175 s. Once the fault is detected, the measurements of the GPS receiver will not be delivered to the master filter anymore until the FDF value is lower than the threshold again. Then the position errors will be corrected gradually by the SINS/Odometer integrated navigation. Figure 9(b) shows the smooth position errors with a precision of 10 m. It is once again verified that the proposed method can detect all the added faults in time, thereby avoiding the defects that the faults have on the navigation results.

Figure 9. Position errors. (a) Using residual chi-squared test. (b) Using the proposed method.
6. CONCLUSIONS
As a guarantee to system reliability, fault detection of the integrated navigation system draws extensive attention. This paper proposes a novel fault detection method based on GPR. In order to avoid the local optimisation, particle swarm optimisation combined with maximum likelihood method is introduced to find the optimal hyper-parameters of the GPR model. FDF is made up of the prediction of GPR, the innovation of the Kalman filter and their variance. Experiments for a SINS/GPS/Odometer integrated navigation system to which the proposed method is applied demonstrate that the method can detect both abrupt faults and gradual faults effectively. Furthermore, the comparison experiments show the FDF of the proposed method is more sensitive to faults than that of the residual chi-squared test, which enhances the advantages of the proposed method. Therefore the system using the proposed method offers more accurate navigation information.
ACKNOWLEDGEMENTS
This work was supported in part by the National Natural Science Foundation of PR China (approval No.61374215).