Introduction
Binary metal-chalcogenide semiconductors are w idely used in optoelectronic devices [Reference Singh, Singh and Sharma1]. Structures containing tetrahedrally coordinated (T d) bonding motifs are often preferable for these applications because they have wide direct band gaps and low electron effective masses, and because they are structurally compatible with other chalcogenide materials. For example, CdTe and CdSe used as absorber layers in thin-film solar cells and ZnS, ZnSe, and CdS used as transport layers in electronics all assume either zinc blende (ZB) or wurtzite (WZ) structures [Reference Lee and Ebong2, Reference Huang, Zhang, Xu, Hou, Wang, Massé, Peng, Liu and Cao3]. Manganese chalcogenides are also compelling materials because they are chemically compatible with other binary chalcogenides and have excellent semiconducting properties. For example, MnO, MnS, and MnSe are wide band gap materials, MnTe exhibits high p-type conductivity, and MnCh (Ch = S, Se, Te) are important for instilling magnetism in semiconductors [Reference Furdyna4]. However, MnCh ground states contain octahedrally coordinated (O h) structural motifs, which are not generally compatible with other commonly used T d structures such as WZ and ZB: MnO, MnS, and MnSe crystallize in the rock salt (RS) structure, and MnTe crystalizes in the nickeline (NC) structure. Besides, the MnCh with O h structures show indirect band gaps [Reference Youn, Min and Freeman5], further hindering their optoelectronic applications. Therefore, stabilizing T d polymorphs of MnCh may enable their future deployment as active optical materials in optoelectronic devices.
There have been several prior reports about changing O h structures (like RS and NC) to T d structures (like ZB and WZ) in MnCh by heterostructural alloying with T d ZnCh leading to novel optoelectronic properties. In the oxides, the insulating RS phase of MnO was changed to the semiconducting WZ phase in the Mn1−xZnxO alloy at Zn compositions above x = 0.3 and applied as water splitting photoelectrodes [Reference Peng, Ndione, Ginley, Zakutayev and Lany6]. Similarly, in the selenides, the RS structure of MnSe was converted to the WZ structure in the Zn1−xMnxSe alloys [Reference Xue, Ye, Medina, Martinez, Lopez-Rivera and Giriat7]. In the tellurides, by alloying NC MnTe with trace amount of ZB ZnTe, the ground state switched from the narrow band gap NC structure to the wide band gap WZ structure [Reference Han, Holder, Siol, Lany, Zhang and Zakutayev8, Reference Sebastian Siol, Han, Mangum, Schulz, Holder, Klein, van Hest and Gorman9]. Despite the success of alloying for stabilization of WZ MnO, MnSe, and MnTe, there is only one report on using alloying to stabilize WZ MnS [Reference Furdyna4]. However, such stabilization of WZ MnS is likely energetically feasible because WZ MnS occurs naturally [Reference Kalinowski10], and has been synthesized via chemical bath deposition [Reference Gümüş, Ulutaş, Esen, Özkendir and Ufuktepe11], heteroepitaxial growth on GaAs [Reference Okajima and Tohda12], and other methods [Reference Beltran-Huarac, Palomino, Resto, Wang, Jadwisienczak, Weiner and Morell13].
Studies demonstrating that structures containing T d motifs can form from alloys containing MnCh end-member compounds with O h motifs have been reported. For example, the WZ structure was observed at intermediate compositions in related MnSe1−xTex alloys formed by alloying RS MnSe and NC MnTe [Reference Siol, Holder, Steffes, Schelhas, Stone, Garten, Perkins, Parilla, Toney and Huey14]. The proposed stabilization mechanism in that case was that the less dense metastable phases (T d polymorphs) can form in alloys of more dense end-member compounds (O h structures) due to the lower competition for space in the less dense phases [Reference Siol, Holder, Steffes, Schelhas, Stone, Garten, Perkins, Parilla, Toney and Huey14]. Depending on the mixing enthalpies and end-member formation energies, this stabilization should also be feasible in iso-structural alloy systems [Reference Siol15]. A computational study was also reported which predicts that T d phases can form by alloying end-member compounds with the same O h structures [Reference Lany16]; however, this theory has not been demonstrated experimentally yet. We also note that alloy stabilization of T d phases by anion substitution (e.g., Se–Te) compared with alloy stabilization by cation substitution (e.g., Mn–Zn) may be more beneficial in optoelectronic devices. This is because in binary compound semiconductors, the conduction band minimum is primarily composed of cation rather than anion states [Reference Youn, Min and Freeman5], so anion alloying may lead to less perturbation of the low electron effective mass in T d structures.
Here, we report the stabilization of a structure with T d bonding motifs in alloys containing two end-member compounds with O h motifs. Specifically, we find that the WZ structure forms at intermediate compositions in MnS1−xSex alloys, despite end-member MnS and MnSe compounds exhibiting RS structures. Structural and optoelectronic properties of MnS1−xSex (0 ≤ x ≤ 1) alloy thin films prepared by combinatorial sputtering are reported as a function of chemical compositions and synthesis temperatures. Although films over the entire MnS1−xSex composition range crystalize in the RS structure at higher synthesis temperature (420 °C), at lower temperatures (280–340 °C) the WZ phase appears at S-rich compositions (x < 0.4). The optical absorption onset of WZ MnS1−xSex alloys is 3.0–3.2 eV, whereas the conductivity is <0.0001 S/cm, indicating its potential for use as a wide band gap semiconductor in various optoelectronic applications. Theoretical mixing enthalpies, electron/hole effective masses, and band gaps are also reported to help better understand the properties of MnS1−xSex alloys, and possible mechanisms of the WZ phase stabilization are discussed.
Results and discussion
Structural properties
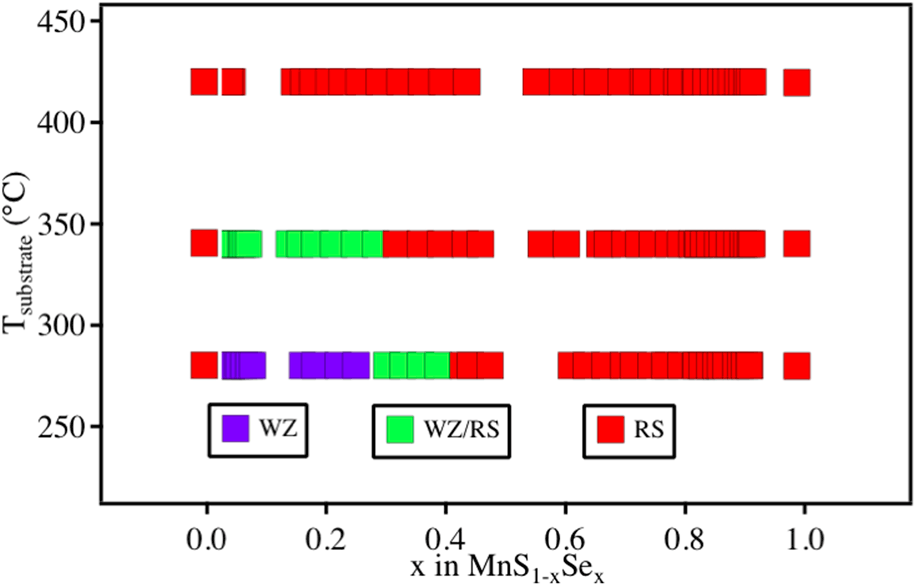
Figure 1(a) shows the synthesis phase map of MnS1−xSex alloys as a function of synthesis temperature and chemical composition, based on the X-ray diffraction (XRD) and X-ray fluorescence (XRF) data. As expected, the MnSe and MnS end-member compounds deposited as reference samples exhibit diffraction patterns corresponding to the ground state RS structure at 280–420 °C. However, their crystal structure changes when they form MnS1−xSex alloys at lower temperatures within this range. At 420 °C, the MnS1−xSex alloys have the RS structure across the entire composition range, the same as the end-member compound, and similar to other isostructural alloys (e.g., WZ AlxGa1−xN [Reference Morko17] or ZB CdTe1−xSex) [Reference Böer18]. At 340 °C, the MnS1−xSex alloys still exhibit peaks indicative of the RS structure through the whole composition range, but an additional signal from a WZ phase is observed at S-rich compositions (x < 0.3). At 280 °C, a similar combination of RS + WZ is observed for 0.3 < x < 0.4, but for x < 0.3, the RS signal disappears completely, and all XRD peaks can be attributed to the WZ-phase. Figure 1(b) shows the XRD heat map for MnS1−xSex alloys synthesized at 280 °C, and similar figures for films grown at 420 °C and 340 °C that were used to populate points in the phase map can be found in Fig. S1 in the Supplementary material (SM). In the past, similar metastable WZ-MnSe1−xTex [Reference Siol, Holder, Steffes, Schelhas, Stone, Garten, Perkins, Parilla, Toney and Huey14] alloys have been shown to decompose into stable parent compounds close to 400 °C. Overall, these results indicate that the WZ phase can be obtained under nonequilibrium growth conditions at lower temperatures, where the phase transformation into the RS ground state is kinetically hindered.

Figure 1: (a) Phase map of MnS1−xSex alloys as a function of chemical composition and synthesis temperature. (b) XRD heat map of MnS1−xSex alloys at 280 °C, showing only WZ peaks appearing at x < 0.3 composition.
To support the WZ phase assignment, a sample with MnS0.92Se0.08 composition synthesized at 280 °C was chosen as the representative for more detailed characterization. Figure 2(a) shows the XRD pattern for this sample as a function of 2Θ angle, with χ angle integration from −126° to −54° (detector at −90°), and a fixed φ angle. The WZ phase shows strong (002) preferential orientation, with only one prominent peak at 2Θ ∼ 30°, similar to WZ MnS thin films reported in the literature [Reference Gümüş, Ulutaş and Ufuktepe19]. Comparison of XRD patterns for WZ-MnS0.92Se0.08 with RS-MnS and RS-MnSe is shown in Fig. S2(a) in SM. To further investigate the phase assignment, an XRD pole figure was collected on a different instrument as a function of φ (0–360°) and χ (0–90°) for the measured 2Θ peak position at ∼30°. Figure 2(b) shows that the peak intensity is strongest at χ = 90°, where the incident and scattered X-ray plane is normal to the substrate surface, further confirming the c-axis preferential orientation of WZ thin films. Similar full-range XRD measurements were conducted for possible 2Θ positions of the RS phase, but none of the other peaks were detected, ruling out the presence of the RS phase in MnS0.92Se0.08 synthesized at 280 °C.

Figure 2: (a) XRD pattern as a function of 2Θ for MnS0.92Se0.08 synthesized at 280 °C, showing strong preferential orientation of WZ phase. (b) Full-range XRD scan as a function of φ and χ at 2Θ ∼ 30° WZ peak for MnS0.92Se0.08 deposited at 280 °C.
The existence of the WZ phase in MnS1−xSex alloys is also supported by selected area electron diffraction (SAED) measurements. Figure 3(a) shows the measured SAED pattern for MnS0.92Se0.08 synthesized at 280 °C and Fig. 3(b) is the simulated reference pattern based on the [100] zone axis of the WZ and RS phase. The measured SAED pattern matches well with the simulated WZ pattern but is different from the RS pattern, and unambiguously confirms the formation of the WZ phase at this composition in MnS1−xSex alloys. However, minor splitting appears for the (0112) peak family, which may be due additional WZ grains with different orientations, or due to minor RS impurity phase. A transmission electron microscopy (TEM) image of this sample point is also provided as Fig. S3 in SM, to show a cross-sectional view of the WZ phase with ∼100-nm grain size that may be possible to increase by annealing. The estimate film thickness from the cross-sectional TEM image is 150 nm, which is similar to 140 nm determined from the XRF model.

Figure 3: (a) SAED patterns of MnS0.92Se0.08 grown at 280 °C. (b) Simulated WZ [100] and RS [100] reference pattern from a single crystal.
Computational results
In an attempt to understand the origin of the appearance of the WZ phase between RS end-member compounds, 0 K mixing enthalpies of MnS1−xSex alloys as function of x (∆H m(x)) were calculated from first principles, and are shown in Fig. 4(a). Generally, the mixing enthalpy of the RS phase is lower than that of the WZ phase along the entire composition range, predicting that the alloys should assume the RS phase under equilibrium conditions at 0 K. For the typical synthesis temperature (280–420 °C), the difference in entropic contribution to the free energy between two solid phases (WZ and RS) is likely to be smaller than the calculated difference in enthalpies of mixing (15–45 meV/at). These computational results are consistent with the measured RS crystal structure of MnS1−xSex alloys synthesized at the higher temperature of 420 °C [Fig. 1(a)]. However, at 280 °C, the WZ phase is experimentally observed (Fig. 1) at sulfur-rich compositions. At this lower temperature, formation of the stable RS structure may be kinetically hindered, facilitating formation of metastable WZ structures of the MnS1−xSex alloys. It is particularly surprising that the WZ phase was observed at S-rich compositions [Fig. 1(b)], where the calculated WZ-to-RS polymorph energy difference is the highest [Fig. 4(a)].

Figure 4: (a) Calculated mixing enthalpy as a function of x in MnS1−xSex. (b) Calculated volume per formula unit as a function of x in MnS1−xSex.
Synthesis of the higher energy WZ polymorph in MnS1−xSex alloys by co-sputtering from RS-MnS and RS-MnSe targets (Fig. 1) is quite surprising in light of our theoretical calculations [Fig. 4(a)], but not uncommon in a broader sense. In general, preferential growth of WZ structure has been observed across different material chemistries (I–VII, II–VI, and II–V) synthesized by a wide range of techniques (solid, liquid, and vapor growths). For example, higher energy WZ polymorphs of I–VII materials (LiBr [Reference Liebold-Ribeiro, Fischer and Jansen20] and InCl [Reference Bach, Fischer and Jansen21]) have been synthesized by crystallization from amorphous precursors deposited by thermal evaporation on cooled substrates. As another example, preference toward WZ polymorph stabilization at low crystal sizes has been observed in pressure-dependent studies of WZ-to-RS transformations of II–VI (CdSe) nanocrystals prepared by colloidal synthesis techniques [Reference Tolbert and Alivisatos22, Reference Chen, Herhold, Johnson and Alivisatos23]. Similar preference of the WZ over the ZB polymorph is also known in vapor–liquid–solid (VLS) growth of III–V (GaAs [Reference Glas, Harmand and Patriarche24] and InAs [Reference Koguchi, Kakibayashi, Yazawa, Hiruma and Katsuyama25]) nanowires. This broad range of materials and methods suggests a universal mechanism of WZ polymorph preference over other possible structures.
We speculate that the formation of the WZ phase at S-rich compositions of co-sputtered MnS1−xSex alloys reported here may be related to Ostwald's “step rule” [Reference Ostwald26]. This rule is based on empirical observations that during the crystallization process metastable structures often form before stable phases. More recently, this rule has been rationalized by measurements of lower surface energies of the metastable polymorphs compared to stable structures [Reference Navrotsky27]. In the case of MnS1−xSex alloys reported here, nucleation of the T d-bonded WZ metastable polymorph may be related to its lower surface energy relative to the O h-bonded polymorph. Such lower surface energy is likely because of the lower number of broken bonds at the surface of a growing particle, but explicit theoretical calculations would be needed to evaluate this hypothesis. This relation to surface energy is also suggested by the observed strong preferential orientation of the MnS1−xSex alloys along (002) WZ and (111) RS growth directions (Fig. 2), which are structurally related and highly polar. More calculations would be required to rule out potential other hypothesis, such as defect-induced stabilization of the WZ polymorph observed here.
Optoelectronic properties
Optical properties of MnS1−xSex were also investigated, both experimentally and theoretically. Figure 5 shows the measured absorption heat map of MnS1−xSex as a function of x where an absorption spectrum at each x is displayed as a false color map. The theoretically predicted band gaps of WZ (direct) and RS (indirect) phases are shown as markers for comparison. At 420 °C, the alloys assume the RS phase across the entire composition range [Fig. 5(a)]. Both the predicted and experimental band gaps decrease nearly linearly as x increases, indicating the weak interaction between elemental constituents in RS MnS1−xSex alloys. This linear change may help to fine-tune optical properties of RS MnS1−xSex alloys, in contrast to the band gap bowing phenomenon commonly observed in other semiconductors due to the alloying interaction effect [Reference Lany16]. The measured absorption onset (defined here as an energy at which the absorption coefficient is 105 cm−1) is comparable between WZ samples [Fig. 5(b)] and RS samples [Fig. 5(a)] at the same compositions, both in the 3.0–3.2 eV range. The experimental and computational optical absorption onset trends appear cross, as the composition is changed from MnS to MnSe, but quantification of these differences is difficult, given the present data. Comparison of optical absorption spectra for WZ–MnS0.92Se0.08 with RS–MnS and RS–MnSe is shown in Fig. S2(b) in SM. Despite the similar absorption onset, WZ alloys have direct optical band gaps, whereas RS alloys have indirect gaps. The direct band gap of the WZ phase enables its potential application in optoelectronic devices.

Figure 5: Optical absorption spectra as a function of x in MnS1−xSex alloys synthesized at (a) 420 °C and (b) 280 °C. The discrete markers are the predicted band gaps of MnS1−xSex alloys in the WZ and RS structures.
Electrical conductivities of the MnS1−xSex alloys synthesized at 420 and 280 °C are summarized in Fig. 6(a). The conductivities of the MnS1−xSex alloys with a WZ structure are lower than the measurement limit of the 4-point probe instrument; thus, it is estimated to be below 0.0001 S/cm. For the MnS1−xSex alloys with a RS structure, the conductivities increase from 0.0001 S/cm to 1 S/cm with increasing x, suggesting that MnSe has shallower defects than MnS. Computationally predicted effective masses of electrons and holes in MnS1−xSex alloys are listed in Fig. 6(b). In MnS1−xSex alloys with a RS structure, the effective masses of electrons and holes both decrease with x, which partly explains the increase of conductivities in Fig. 6(a). For the MnS1−xSex alloys with a WZ structure, both effective masses are relatively insensitive to chemical composition x, and hole effective mass is quite scattered. This scatter may be related to finite size effect in supercell-based alloy calculations (Fig. S4), which may be amplified in WZ valence band due to p–d coupling effects [Reference Wei and Zunger28]. It is also noteworthy that the effective mass of electrons in the WZ structure (0.3m 0 at x = 0.2) with a direct band gap is much lower than that of electrons in the RS structure (1.5m 0 at x = 0.2) with an indirect band gap, suggesting potential optoelectronic applications of WZ alloys if they could be doped n-type. Such differences in effective masses between tetrahedrally coordinated (WZ and ZB) and octahedrally coordinated (RS and NC) polymorphs have been reported in other binary chalcogenides [Reference Han, Holder, Siol, Lany, Zhang and Zakutayev8, Reference Siol, Holder, Steffes, Schelhas, Stone, Garten, Perkins, Parilla, Toney and Huey14] and in ternary nitrides [Reference Bauers, Holder, Sun, Melamed, Woods-Robinson, Mangum, Perkins, Tumas, Gorman, Tamboli, Ceder, Lany and Zakutayev29, Reference Arca, Perkins, Lany, Mis, Chen, Dippo, Partridge, Sun, Holder, Tamboli, Toney, Schelhas, Ceder, Tumas, Teeter and Zakutayev30, Reference Heinselman, Lany, Perkins, Talley and Zakutayev31].

Figure 6: (a) Measured electrical conductivity of MnS1−xSex alloys with the RS structure as a function of x. (b) Computationally predicted density of states effective masses (m*) of electrons and holes in MnS1−xSex alloys with RS and WZ structures.
Summary
The structural and optoelectronic properties of MnS1−xSex alloys (0 ≤ x ≤ 1) as a function of chemical composition and synthesis temperature are reported. Despite the fact that the end-member compounds MnS and MnSe assume RS as the experimentally observed and calculated ground state structure, a metastable WZ structure appears at S-rich compositions grown at a lower temperature of 280 °C. This is in contrast to higher temperature growths at 420 °C where the alloys remain in the RS over the entire composition range. The stabilization of the WZ-phase at lower deposition temperatures is surprising in light of theoretical calculations that predict the mixing enthalpy for WZ structures to be higher than for RS structures at all compositions. The stabilization of WZ polymorph may be attributed to lower surface energy of the WZ structure compared with the RS structure, as observed in other materials. In addition, the higher density of RS structure may account for the preference of the formation of WZ phase at S-rich compositions. Computationally predicted band gaps of MnS1−xSex alloys in RS and WZ structures correlate well with the experimentally measured optical absorption onsets. In addition, the RS MnS1−xSex alloys are measured to be more electrically conductive for the Se-rich composition, and calculated electron and hole effective masses are consistent with this observation.
Methods
Experiments
MnS1−xSex (0 ≤ x ≤ 1) alloys were prepared by combinatorial RF sputtering (AJA International, Orion 8). Two sputter targets with a diameter of 50.8 mm, one of MnSe and one of MnS, were placed opposite to each other in confocal geometry to generate a composition gradient covering the entire composition range in 3–4 depositions. The sputtering power was 8–50 W. For end-member samples, only a single source was used. Fused silica was used as substrates and partially mounted on the sample platen by silver paint. This partial contact induces a thermal gradient across the substrate orthogonal to the composition gradient. The sample platen and substrates were heated by a SiC heater to achieve the maximum substrate surface temperatures of 420 °C, 340 °C, and 280 °C. The chamber was pumped down to a base pressure of <1 × 10−6 torr before thin films were deposited in high-purity Ar at a working pressure of 1.3 × 10−3 torr and an Ar flow rate of 16 sccm. The target–substrate distance was 134 mm. More detailed synthesis information can be found in our previous papers [Reference Han, Siol, Zhang and Zakutayev32, Reference Han, Matthews, Roberts, Talley, Bauers, Perkins, Zhang and Zakutayev33].
After synthesis, the MnS1−xSex thin-film libraries were characterized as a function of position at 44 locations on a rectangular 4 × 11 grid. Thin-film properties obtained from these mapping techniques included: composition and thickness measurement by X-ray fluorescence (XRF; Fischerscope XDV-SDD), crystal structure measured by X-ray diffraction (XRD; Bruker D8) with Cu Kα radiation and a 2D detector in an approximate Bragg-Brentano geometry, optical transmittance and reflectance measured by a custom UV-Vis instrument using ocean optics spectrometers covering wavelengths of 300–1100 nm, and sheet resistance collected by a custom 4-point probe instrument [Reference Zakutayev, Luciano, Bollinger, Sigdel, Ndione, Perkins, Berry, Parilla and Ginley34]. The XRF measurements of MnS1−xSex alloy composition were verified by measuring MnS and MnSe parent compounds with known composition, and the XRF-derived thickness was verified by a cross-sectional TEM measurement. The absorption spectra and electrical conductivities were determined from these measurements based on thickness data obtained from XRF. The large amounts of data that resulted from spatially resolved characterization were analyzed using the COMBIgor software package (https://www.combigor.com/) [Reference Talley, Bauers, Melamed, Papac, Heinselman, Khan, Roberts, Jacobson, Mis and Brennecka35] and will be made publicly available at HTEM DB (https://htem.nrel.gov/) [Reference Zakutayev, Wunder, Schwarting, Perkins, White, Munch, Tumas and Phillips36].
The X-ray pole figure of the WZ (002) peak was collected on a Rigaku Smartlab diffractometer using Cu-Kα radiation and at 2Θ = 30°. TEM was performed on a FEI Tecnai ST30 at 300 kV. A Pt capping layer was deposited on the surface of the samples to protect the thin-film structure. TEM lamella were prepared by the standard focused ion beam (FIB) lift-out technique and followed by Ga ion milling to reduce the final thickness to less than 100 nm. Then, a Fischione Nanomill was used to remove preparation damage on the TEM foils using low energy cleaning at 500 eV under vacuum of 10−7 torr at −170 °C for ±10°.
Computations
Periodic boundary condition density functional theory calculations were performed within the Vienna Ab Initio Simulation Package [Reference Kresse and Furthmüller37] (VASP) using projector augmented-wave (PAW) pseudopotentials [Reference Kresse and Joubert38]. To obtain accurate polymorph energies of MnS and MnSe polymorphs, we used the random phase approximation based on the adiabatic-connection fluctuation–dissipation theorem (RPA-ACFDT) [Reference Harl and Kresse39]. For RPA calculations of MnS, the energy cutoff for the plane-wave basis was 360 eV while the energy cutoff for the response function was 240 eV with a 4 atom unit cell. DFT + U with U = 3 eV for Mn-d orbitals was utilized as the input wave function for obtaining the Hartree Fock energy and the ACFDT-RPA correlation energy. The energy difference with respect to the magnetic ground state was determined at the DFT + U level and subtracted from the RPA energy. Polymorph energies for MnSe were calculated in a previous publication in a similar way [Reference Siol, Holder, Steffes, Schelhas, Stone, Garten, Perkins, Parilla, Toney and Huey14].
For calculations of MnSxSe1−x alloy energetics, we used the Perdew–Burke–Ernzerhof (PBE) generalized gradient approximation exchange-correlation functional with a Hubbard correction of U = 3 eV for Mn-d orbitals [Reference Perdew, Burke and Ernzerhof40]. Mixing enthalpies were calculated using a 96 atom supercell with random cation configurations generated using the special quasirandom structures method [Reference Zunger, Wei, Ferreira and Bernard41]. Calculations were conducted at 17 compositions across the phase space for each crystal structure. Calculations utilized a Gamma centered 2 × 2 × 2 k-point mesh with an energy cutoff of 400 eV. Alloy interaction parameters (Ω) for each polymorph were determined by fitting ΔH m(x) using a second-order polynomial.
The theoretical band gaps and DOS effective masses of the alloys were calculated through a linear weighting of the DFT-predicted values to the end-member calculated within the GW approximation [Reference Shishkin and Kresse42]. For density of states effective mass calculations, a denser k-mesh with 1000 k-points per reciprocal atom was used, and the results obtained from an energy window corresponding to effective temperatures of 500–3000 K. Correcting the GW self-energy with an attractive on-site potential for the d orbitals has been shown to result in accurate band gaps for transition metal compounds which are generally underestimated by DFT, as described in detail in prior publications [Reference Lany43]. However, the GW method is computationally prohibitive for the large supercells required for the alloys studied here. Therefore, the GW-computed values of the end-members were used to correct the DFT values for the alloys across the composition space. The computational results of the GW approximation are available from the NREL materials database (http://materials.nrel.gov) [Reference Lany43, Reference Lany44]. The “effective GW” band gaps and effective masses for alloys of MnS1−xSex are given by a simple linear weighting:  $E_x^{{\rm{GW}}} = E_x^{{\rm{DFT}}} \left( {x{{E_{x = 1}^{{\rm{GW}}} } \over {E_{x = 1}^{{\rm{DFT}}} }} + {{\left( {1 - x} \right)E_{x = 0}^{{\rm{GW}}} } \over {E_{x = 0}^{{\rm{DFT}}} }}} \right)$, as described in previous publications [Reference Matthews, Holder, Schelhas, Siol, May, Forkner, Vigil-Fowler, Toney, Perkins and Gorman45]. This approach is reasonable because the band gaps and effective masses are underestimated by DFT, but the changes in the electronic structure across the composition range are generally correct in these materials.
$E_x^{{\rm{GW}}} = E_x^{{\rm{DFT}}} \left( {x{{E_{x = 1}^{{\rm{GW}}} } \over {E_{x = 1}^{{\rm{DFT}}} }} + {{\left( {1 - x} \right)E_{x = 0}^{{\rm{GW}}} } \over {E_{x = 0}^{{\rm{DFT}}} }}} \right)$, as described in previous publications [Reference Matthews, Holder, Schelhas, Siol, May, Forkner, Vigil-Fowler, Toney, Perkins and Gorman45]. This approach is reasonable because the band gaps and effective masses are underestimated by DFT, but the changes in the electronic structure across the composition range are generally correct in these materials.
Supplementary material
To view the supplementary material for this article, visit https://doi.org/10.1557/jmr.2019.402.
Acknowledgments
This work was supported by the U.S. Department of Energy under Contract No. DE-AC36-08GO28308 with Alliance for Sustainable Energy, LLC, the Manager and Operator of the National Renewable Energy Laboratory. Funding provided by Office of Science, Office of Basic Energy Sciences, as part of the Energy Frontier Research Center “Center for Next Generation of Materials Design: Incorporating Metastability.” Y.H. thanks the China Scholarship Council for offering the stipend to perform research at the National Renewable Energy Laboratory. S.L.M. also acknowledges the support from the U.S. Department of Energy's Office of Energy Efficiency and Renewable Energy, Fuel Cells Technologies Office Award No. DE-EE0008088, “Computationally Accelerated Discovery and Experimental Demonstration of High-Performance Materials for Advanced Solar Thermochemical Hydrogen Production.” The computational research was performed using resources sponsored by the Department of Energy's Office of Energy Efficiency and Renewable Energy and located at the National Renewable Energy Laboratory. The authors would like to thank Angela Fioretti, Kevin Talley, and Yun Xu for useful discussions and valuable suggestions. The views expressed in the article do not necessarily represent the views of the DOE or the U.S. government.