Hostname: page-component-8448b6f56d-m8qmq Total loading time: 0 Render date: 2024-04-24T14:46:24.830Z Has data issue: false hasContentIssue false
  • English
  • Français

Rotation field in wedge indentation of metals

Published online by Cambridge University Press:  23 September 2011

Narayan Sundaram ,
Yang Guo ,
Tejas G. Murthy ,
Chris Saldana  and
Srinivasan Chandrasekar
Narayan Sundaram
Affiliation:
Center for Materials Processing and Tribology, Purdue University, West Lafayette, Indiana 47907
Yang Guo
Affiliation:
Center for Materials Processing and Tribology, Purdue University, West Lafayette, Indiana 47907
Tejas G. Murthy
Affiliation:
Department of Civil Engineering, Indian Institute of Science, Bangalore 560 054, India
Chris Saldana
Affiliation:
Department of Industrial and Manufacturing Engineering, The Pennsylvania State University, University Park, Pennsylvania 16802
Srinivasan Chandrasekar*
Affiliation:
Center for Materials Processing and Tribology, Purdue University, West Lafayette, Indiana 47907
*
a)Address all correspondence to this author. e-mail: chandy@purdue.edu
Get access

Abstract

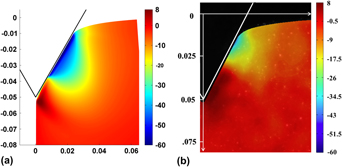
A study is made of the rotation field in wedge indentation of metals using copper as the model material system. Wedges with apical angles of 60° and 120° are used to indent annealed copper, and the deformation is mapped using image correlation. The indentation of annealed and strain-hardened copper is simulated using finite element analysis. The rotation field, derived from the deformation measurements, provides a clear way of distinguishing between cutting and compressive modes of deformation. Largely unidirectional rotation on one side of the symmetry line with small spatial rotation gradients is characteristic of compression. Bidirectional rotation with neighboring regions of opposing rotations and locally high rotation gradients characterizes cutting. In addition, the rotation demarcates such characteristic regions as the pile-up zone in indentation of a strain-hardened metal. The residual rotation field obtained after unloading is essentially the same as that at full load, indicating that it is a scalar proxy for plastic deformation as a whole.

Keywords

NanoindentationHardnessSimulation
Type
Articles
Information
Journal of Materials Research , Volume 27 , Issue 1: Focus Issue: Instrumented Indentation , 14 January 2012 , pp. 284 - 293
Copyright
Copyright © Materials Research Society 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

1.Oliver, W.C. and Pharr, G.M.: An improved technique for determining hardness and elastic modulus using load and displacement sensing indentation experiments. J. Mater. Res. 7, 1564 (1992).CrossRefGoogle Scholar
2.Fischer-Cripps, A.C.: Nanoindentation (Springer-Verlag, New York, 2004).CrossRefGoogle Scholar
3.Tabor, D.: The Hardness of Metals (Oxford Univ. Press, Oxford, 1951).Google Scholar
4.Tabor, D.: Indentation hardness: Fifty years on a personal view. Philos. Mag. A 74, 1207 (1996).CrossRefGoogle Scholar
5.Hill, R., Lee, E.H., and Tupper, S.J.: The theory of wedge indentation of ductile materials. Proc. R. Soc. London, Ser. A 188, 273 (1947).Google Scholar
6.Mulhearn, T.O.: The deformation of metals by vickers-type pyramidal indenters. J. Mech. Phys. Solids 7, 85 (1959).CrossRefGoogle Scholar
7.Hirst, W. and Howse, M.G.J.W.: The indentation of materials by wedges. Proc. R. Soc. London, Ser. A 311, 429 (1969).Google Scholar
8.Haddow, J.B.: On a plane strain wedge indentation paradox. Int. J. Mech. Sci. 9, 159 (1967).CrossRefGoogle Scholar
9.Johnson, K.L.: Contact Mechanics (Cambridge Univ. Press, Cambridge, 1985).CrossRefGoogle Scholar
10.Samuels, L.E. and Mulhearn, T.O.: An experimental investigation of the deformed zone associated with indentation hardness impressions. J. Mech. Phys. Solids 5, 125 (1957).CrossRefGoogle Scholar
11.Atkins, A.G. and Tabor, D.: Plastic indentation in metals with cones. J. Mech. Phys. Solids 13, 149 (1965).CrossRefGoogle Scholar
12.Chaudhri, M.M.: Subsurface deformation patterns around indentations in work- hardened mild steel. Philos. Mag. Lett. 67, 107 (1993).CrossRefGoogle Scholar
13.Chaudhri, M.M.: Subsurface plastic strain distribution around spherical indentations in metals. Philos. Mag. A 74, 1213 (1996).CrossRefGoogle Scholar
14.Lee, S., Hwang, J., Shankar, M.R., Chandrasekar, S., and Compton, W.D.: Large strain deformation field in machining. Metall. Mater. Trans. A 37, 1633 (2006).CrossRefGoogle Scholar
15.Murthy, T.G., Huang, C., and Chandrasekar, S.: Characterization of deformation field in plane strain indentation of metals. J. Phys. D: Appl. Phys. 41, 074026 (2008).CrossRefGoogle Scholar
16.Murthy, T.G., Madariaga, J., and Chandrasekar, S.: Direct mapping of deformation in punch indentation and correlation with slip line fields. J. Mater. Res. 24, 760 (2009).CrossRefGoogle Scholar
17.Follansbee, P.S. and Sinclair, G.B.: Quasi-static normal indentation of an elastic-plastic half-space by a rigid sphere. Int. J. Solids Struct. 20, 81 (1984).CrossRefGoogle Scholar
18.Mata, M., Anglada, M., and Alcala, J.: Contact deformation regimes around sharp in- dentations and the concept of the characteristic strain. J. Mater. Res. 17, 964 (2002).CrossRefGoogle Scholar
19.Jiang, J., Sinclair, G., and Meng, W.: Quasi-static normal indentation of an elasto-plastic substrate by a periodic array of elastic strip punches. Int. J. Solids Struct. 46, 3677 (2009).CrossRefGoogle Scholar
20.Lubliner, J.: Plasticity Theory. 2nd ed. (Mineola, NY: Dover, 2008).Google Scholar
21.Bower, A.: Applied Mechanics of Solids (CRC Press, Boca Raton, FL, 2009).CrossRefGoogle Scholar
22.Thomsen, E.G., Yang, C.T., and Kobayashi, S.: Mechanics of Plastic Deformation in Metal Processing (Macmillan, New York, 1965).Google Scholar
23.Hill, R.: The Mathematical Theory of Plasticity (Oxford Univ. Press, Oxford, 1950).Google Scholar
24.Brown, L.M.: Transition from laminar to rotational motion in plasticity. Philos. Trans. R. Soc. London, Ser. A 355, 1979 (1997).CrossRefGoogle Scholar