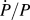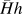A. Rationalization of a sudden transition to dislocation-mediated flow

Figure 1 shows the hardness, H, as a continuous function of indentation depth, h, measured at a targeted $\dot{P}{\rm{/}}P$ of 0.05 s⁻¹. The triangular data points represent the average of 56 measurements and the scatter bars span one standard deviation about the mean. The individual curves (small circular data points) represent 6 of the 56 measurements used to calculate the average H. Illustrated by the individual curves, the sudden transition from diffusion to dislocation-mediated flow occurs with an abrupt avalanche of dislocation motion and a simultaneous drop in the mean pressure. We note this observation is very similar to the indentation behavior of indium (tetragonal, rather than the body centered cubic crystal structure and T _H = 0.69 at room temperature) previously reported by Feng and Ngan.^{Reference Feng and Ngan10} Here, the stress and depth at which the transition occurs as well as the magnitude of the ensuing pressure drop clearly varies from one test site to the next, presumably in a manner that directly reflects the details of the defect structure in the volume of the material being sampled by the indenter. The inflection point in the average H corresponds to the average depth at which the sudden transition from diffusion to dislocation-mediated flow occurs. As previously reported,^{Reference Herbert, Hackney, Dudney, Thole and Phani3} the average H as a function of depth and position across the surface of the specimen is quite repeatable despite the large scatter shown in Fig. 1. On average and in a manner that depends on the indentation strain rate, the mean contact pressure required to initiate the dislocation-mediated flow at a T _H of 0.67 is found to range from approximately 44 to 104 MPa (this range decreases slightly, from 40 to 90 MPa, when the displacement burst filter described in Sec. III.B. is not considered).

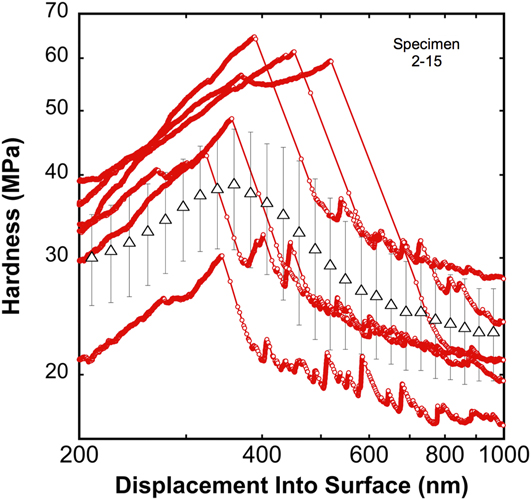
FIG. 1. The hardness of a 5 μm thick high-purity vapor deposited Li film on a glass substrate. Measured at T _H = 0.67 and a targeted $\dot{P}{\rm{/}}P$ of 0.05 s⁻¹. Averaged results (triangular data points) and 6 of 56 individual curves that illustrate the abrupt transition from diffusion to dislocation-mediated flow.

The plastic deformation before the strain burst (pop-in) has been rationalized using diffusional creep mechanisms.^{Reference Herbert, Hackney, Dudney, Thole and Phani3} A natural outcome of that rationalization is that prior to the strain burst, there is little to no change in the dislocation density. As such, there is no elastically constrained volume of plastically deformed Li beneath the indenter and, therefore, the constraint factor relating H to the flow stress of Li is taken to be 1. Assuming the yield strength of bulk polycrystalline Li is 0.5 MPa near room temperature, a constraint factor of 1 means the mean pressure required to initiate dislocation-mediated plasticity ranges from approximately 88 to 208 times higher than the yield stress of bulk polycrystalline Li.

These high pressures are generally consistent with the results from microcompression experiments recently performed by Xu et al.^{Reference Xu, Ahmad, Aryanfar, Viswanathan and Greer1} on single crystal Li pillars (height to diameter ratios between 3:1 & 5:1) at a T _H of 0.66 (T = 26 °C). Examined under a constant nominal strain rate of 5 × 10⁻³ s⁻¹, their results show the compressive yield strength increases from 15 to 105 MPa as the pillar diameter decreases from 9.45 to 1.39 μm (approximately 30–210 times larger than the yield stress of bulk polycrystalline Li). Similar to the nanoindentation results, the onset of dislocation-mediated flow in the pillars is concomitant with an apparent avalanche of dislocation motion. Post-test images clearly show slip-offsets in the pillars that are oriented at or near 45° to the applied load. As explained by Xu, the size-dependent strength of the pillars may be the direct result of a low initial dislocation density and, hence, dislocation nucleation governed plasticity. We also note that due to the high T _H and the potentially low dislocation density, creep mechanisms such as Nabarro–Herring and Harper–Dorn could contribute to the deformation of the pillar prior to the onset of dislocation-mediated flow.

The results from the indentation experiments represent five data sets comprising a total of 268 measurements performed at three targeted values of $\dot{P}{\rm{/}}P$, 0.05, 0.5, and 1.0 s⁻¹, and a constant loading rate of 12.5 μN/s. Figure 2 shows the average avalanche stress (H) and the corresponding average avalanche depth at the onset of dislocation-mediated flow for two films and five strain rates. As previously reported, due to the nature of the loading algorithms and the depth-dependent H, the indentation strain rates are unavoidably depth dependent.^{Reference Herbert, Hackney, Dudney, Thole and Phani3} The values of $\dot{h}{\rm{/}}h$ immediately prior to the avalanche are reported in Fig. 2. As the data show, there is a significant size effect in that the transition or avalanche stress varies with depth, with a power-law exponent of −1.17. This value is nearly double that observed in the microcompression experiments performed by Xu et al.^{Reference Xu, Ahmad, Aryanfar, Viswanathan and Greer1} (−0.68 at a slightly lower T _H), but rather than being related to the physical dimensions of the test specimen, the size effect observed here is controlled by the size of the indentation stress field in relation to the defect structure being sampled by the indenter.^{Reference Phani, Johanns, George and Pharr4} Following the logic proposed by Bragg^{Reference Bragg11} in 1942, argued by El-Awady^{Reference El-Awady7} in 2015, and demonstrated by Li et al.^{Reference Li, Bushby and Dunstan8} in 2016, the power law exponent of −1.17 is generally consistent with the Orowan mechanism. That is to say the stress level required to activate the weakest dislocation source is inversely proportional to the source length and its inherent curvature, both of which are in turn bounded by the physical dimensions of the stress field responsible for activating the source.^{Reference Li, Bushby and Dunstan8}

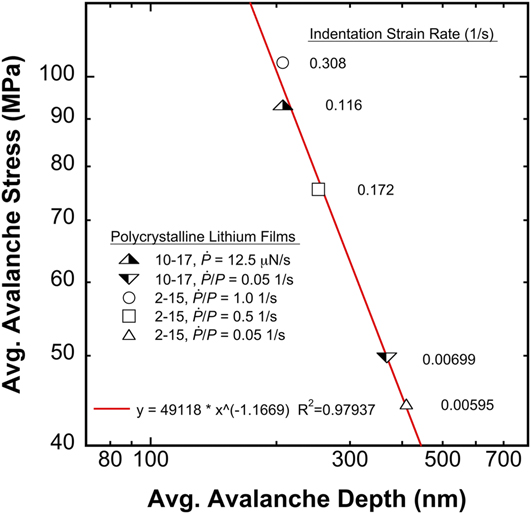
FIG. 2. High-purity vapor deposited Li. Power-law dependence between the average indentation pressure and depth at which the transition from diffusion to dislocation-mediated flow occurs.

As proposed by Stricker and Weygand^{Reference Stricker and Weygand6} in 2015 and in general agreement with the literature review of “Plasticity in Confined Dimensions,” by Kraft et al.^{Reference Kraft, Gruber, Mönig and Weygand5} in 2010, we note the dislocation avalanche and simultaneous pressure drop is consistent with dislocation multiplication enabled by a glissile junction that effectively operates as a Frank–Read source. The strength-controlling dimension would thus be the distance between the pinning points of the junction, as this length determines the curvature of the dislocation and, therefore, the stress level required to activate it. As shown in Fig. 3, the CDF for the stress level required to initiate dislocation-mediated flow exhibits an inflection point with each of the examined strain rates. The observed inflection point suggests a peak in the probability density function. For a Weibull distribution, it is then expected that the shape parameter will be near 3. Moreover, the shift of the distribution tail from the origin of the CDF indicates a minimum stress for the initiation of the avalanche, or a nonzero location parameter. A three-parameter Wiebull distribution of the form

(1)$$P = 1 - \exp \left[ { - \lambda V{{\left( {{{\sigma - {\sigma _{{\rm{location}}}}} \over {{\sigma _{{\rm{scale}}}}}}} \right)}^3}} \right]\quad ,$$

is thus proposed, where P is the cumulative probability, λ is a “critical flaw” number density, and V is the stressed volume. As pointed out by Ngan et al.,^{Reference Ngan, Zuo and Wo12} Weibull statistics are frequently used in precisely this manner to determine the probability of failure (plastic flow) observed in micropillar and nanoindentation experiments. Of particular interest here, we note that Todinov^{Reference Todinov13} has demonstrated how the stress terms in a Weibull analysis can be correlated with the length scale of the material defect. Following Todinov’s approach as applied to the dislocation source length scale, a physical interpretation of Eq. (1) is possible by hypothesizing that initiation of the transition or avalanche event represents the activation of a Frank–Read source. The mean pressure under the indenter, σ, and the location and scale parameters can then be linked with the dislocation pinning point spacing, L, through

(2)$$\sigma = {{Gb} \over L}\quad ,$$

(3)$${\sigma _{{\rm{location}}}} = {{Gb} \over {{L_{\max }}}}\quad ,$$

and

(4)$${\sigma _{{\rm{scale}}}} = {{Gb} \over {{L_{{\rm{ave}}}}}}\quad ,$$

where G is the shear modulus, taken to be 4.25 GPa, b is the magnitude of the Burgers vector, taken to be 3.04 Å, L _max is the maximum spacing for which the entire looping process can occur, and σ_scale is the stress that would activate the Frank–Read source having the average length, L _ave, in the L distribution (this is not necessarily the average stress). Letting L _max = βh and V scale as h ³, where h is the average depth observed for the avalanche, Eq. (1) can now be rewritten as

(5)$$P = 1 - \exp \left[ { - \lambda {L_{{\rm{ave}}}}^3{{\left( {{{Hh} \over {Gb}} - {1 \over \beta }} \right)}^3}} \right]\quad ,$$

where β is a dimensionless constant that correlates the depth at which the avalanche occurs with the required width of the Frank–Read source capable of completing the entire loop process. Taking values of P near 0.2 and 0.8 for each data set, Eq. (5) was used to solve for β and the product, $\lambda {L_{{\rm{ave}}}}^3$. The values of the calculated terms are shown in Table I and, as shown in Fig. 4, the measured and predicted CDFs compare very well. We, therefore, conclude that Eq. (5) offers one possible rationalization for the mechanism that enables the unique transition from diffusion to dislocation-mediated flow. We also note that evaluation of the proposed CDF at the Weibull mean value, $\bar{H}$, yields

(6)$$\bar{H}h = {{Gb\left( {{{0.885} \over {{L_{{\rm{ave}}}}}} + {{{\lambda ^{1{\rm{/}}3}}} \over \beta }} \right)} \over {{\lambda ^{1{\rm{/}}3}}}}\quad ,$$

which directly suggests that the approach is self-consistent in the sense that Eq. (6) predicts the result observed in Fig. 2, where the product $\bar{H}h$ from all five strain rates is nearly a constant, 19.3 N/m ± 6.8%. The experimentally determined values of $\bar{H}h$ are provided in Table I. The implication here is that the avalanche process is correlated with the strain rate through the generation of different diffusion-controlled H–h pathways and that the effect of strain rate on the dislocation source distribution, argued as the Frank–Read source CDF in this paper, has a relatively weak contribution to the observed behavior.

FIG. 3. Experimentally measured CDFs of the indentation pressure (stress) at the sudden transition from diffusion to dislocation-mediated flow.

TABLE I. Values of β and λL _ave³ used to calculate the CDF of the transition stress as per Eq. (5) and the experimentally measured Weibull mean value, $\bar{H}h$.

FIG. 4. CDFs of the indentation pressure (stress) at the sudden transition from diffusion to dislocation-mediated flow: Direct comparisons between the experimentally measured CDFs and rationalizations based on the activation of a Frank–Reed source at the transition stress.

B. Displacement burst filter

As previously noted, the magnitude of the displacement burst and the ensuing pressure drop are observed to vary from one test location to the next. We submit not all of the displacement bursts are the result of the proposed Frank–Read mechanism, as some could certainly be caused by traditional or single source dislocation motion. To identify the bursts most likely associated with dislocation multiplication consistent with Frank–Read source looping, a simple metric was used to eliminate measurements that did not meet a minimum plastic strain requirement. Here we use the Orowan equation to express the plastic strain associated with the displacement burst as ε_plastic = (h _burst/h _burst³)b(2h _burst). The product Gε_plastic then corresponds to the pressure drop due to the limited dislocation motion and is taken as the threshold for consideration of dislocation multiplication. Thus, only pressure drops meeting the criteria, (H _{before burst} − H _{after burst}) > 2Gb/h _burst are considered. Based on this test-specific metric, 82% of the 325 measurements of h–H burst coordinates performed were found to meet the necessary although not necessarily sufficient criterion for the activation of a Frank–Read source. We note the average values of H _burst and h _burst with and without the elimination are generally similar, but without the elimination the power law exponent in Fig. 2 decreases by ∼11%, from −1.17 to −1.3.

As previously reported, it should be noted that the experimentally estimated pressure drop is overestimated due to the effect of dynamic overload when a displacement burst occurs. The analysis leading to the elimination metric described above is thus inexact. While it is theoretically possible that a displacement-controlled experiment could mitigate or even potentially eliminate dynamic overload, it could only be achieved if the instrument’s measurement and control time constants are significantly faster than the time-scale of the displacement burst. At the time of this writing, no known such controller and actuator exist.

C. Grain boundaries act as a dislocation source

Figure 5 is an optical micrograph showing ∼220 nm deep residual hardness impressions in one of the largest grains of an 18 μm thick Li film. Under a targeted $\dot{P}{\rm{/}}P$ of 0.05 s⁻¹, the grain interior and boundary were sampled 28 and 68 times, respectively. As the image shows, the test sites are generally within 1–3 μm of the grain boundary and the orientation of the tip relative to the boundary changes from one test site to the next. Figure 6 directly compares CDFs of the avalanche stress as measured in the grain interior and near the boundary. Although estimating the magnitudes and physical dimensions of the elastic stress field under load is difficult due to the diffusional creep, the CDFs shown in Fig. 6 clearly indicate that the boundary acts as a dislocation source at 31 °C, as indents positioned near the boundary require less stress to initiate the transition to dislocation-mediated flow. As explained by Hirth and Lothe,^{Reference Hirth14} a variety of grain boundary sources exist. Among the possibilities are stress concentrations at the boundary that preferentially operate nucleation sources or small angle nets acting as Frank–Read sources. We further note that this observation is generally consistent with nanoindentation studies and atomistic simulations performed on gold films.^{Reference Lilleodden and Nix15}

FIG. 5. Optical micrograph of ∼220 nm deep indents in a high-purity vapor deposited 18 μm thick Li film on a glass substrate: 28 indents in the interior of the grain and 68 indents in close proximity to the grain boundary.

FIG. 6. Direct comparison between the experimentally measured CDFs of the indentation pressure (stress) at the sudden transition from diffusion to dislocation-mediated flow in the grain interior versus close proximity to the grain boundary. This result clearly indicates that the grain boundary acts as a dislocation source.

D. Implications of lithium’s mechanical behavior at small length scales in relation to potential failure mechanisms of SEs

The unique mechanical behavior of Li at small length scales and high T _H is of particular interest because of its potential impact on the performance of energy storage devices. During charging, gradients in the chemical potential will force Li to preferentially diffuse into defects at the Li/SE interface. In a manner that depends on the length scale of the interfacial defect and the imposed strain rate, the reported results show at a T _H of 0.67 and an initially low dislocation density (ρ ≤ 1.1 × 10¹² m⁻²), Li can support pressures ranging from ∼46 to 350 times higher than the nominal yield strength of bulk polycrystalline Li.^{Reference Herbert, Hackney, Dudney, Thole and Phani3} The highest pressures developing in the smallest interfacial defects exposed to the highest strain rates. Here we propose the strain rate is directly coupled to the charging current density.

Grain boundaries, grain boundary grooving, porosity, and scratches in the SE separator are among the potential small-scale defects disrupting the local Li/SE interface morphology. During charging, these defects would become filled with metallic Li at a rate that depends on the current density. Here we assume the constraint afforded by the high elastic modulus of the SE separator inhibits volume expansion of the Li inside the defect and results in a hydrostatic pressure component analogous to that of a rigid, thick-walled pressure vessel, with hoop stresses developing at the Li/SE interface. The difference from the pressure vessel analogy is that the hydrostatically stressed Li is open to the planar Li film outside the defect, allowing for the possibility of stress relief by diffusion or dislocation-mediated flow.

For an interfacial defect in the physical form of a groove with a radius, R, and a fixed length, L, the time dependence of the volumetric strain due to an increase in R caused by the influx of Li may be written in terms of the current density (to a first order approximation) as

(7)$${{\rm{d}} \over {{\rm{d}}t}}{{\Delta V} \over V} = {2 \over R}{{{\rm{d}}R} \over {{\rm{d}}t}} = {2 \over R}{{iA\Omega } \over F}\quad ,$$

where i is the charging current density (i < 0), A is Avogadro’s number, Ω is the atomic volume of Li, and F is the Faraday constant. In the absence of any plasticity, the radial elastic strain rate due to the incorporation of Li within the groove is

(8)$${\dot{\varepsilon }_{{\rm{elastic}}}} = {2 \over R}{{{\rm{d}}R} \over {{\rm{d}}t}} = {2 \over R}{{iA\Omega } \over F}\quad .$$

Using the previously adopted conservation of strain approach,^{Reference Herbert, Hackney, Dudney, Thole and Phani3} $\left| {{{\dot{\varepsilon }}_{{\rm{elastic}}}}} \right| = \left| {{{\dot{\varepsilon }}_{{\rm{total}}}}} \right| - \left| {{{\dot{\varepsilon }}_{{\rm{plastic}}}}} \right|$, it naturally follows that if plasticity contributes to the change in R, then

(9)$$\left| {{{\dot{\varepsilon }}_{{\rm{elastic}}}}} \right| = \left| {{2 \over R}{{iA\Omega } \over F}} \right| - \left| {{{\dot{\varepsilon }}_{{\rm{plastic}}}}} \right|\quad .$$

In the case of a kinetically limited plasticity mechanism for relief of the hydrostatic pressure, p, the time dependence of the hydrostatic pressure due to charging is then

(10)$$\left| {{{{\rm{d}}p} \over {{\rm{d}}t}}} \right| = K\left[ {\left| {{2 \over R}{{iA\Omega } \over F}} \right| - \left| {{{\dot{\varepsilon }}_{{\rm{plastic}}}}} \right|} \right]\quad ,$$

where K is the bulk modulus. A simple Thevenin equivalent circuit model for charging (i < 0) applied locally at the groove is proposed for extending the analysis to consider the relationship between stress relief mechanisms and the electrochemical parameters in the most transparent manner. The charging voltage is correlated with the current density at the groove through

(11)$${V_{{\rm{applied}}}} = {\rm{OCV}} - {{i\left( {2\pi RL} \right){R_{{\rm{BattA}}}}} \over {2\pi RL}}\quad ,$$

where R _BattA is the area specific battery internal resistance (Ohm m² = (J s)/C² m²) and OCV is the open circuit voltage. The OCV is a function of the hydrostatic stress at the groove (P < 0), given by

(12)$${\rm{OCV}} = {\rm{OC}}{{\rm{V}}_{\rm{o}}} - {{\Omega pA} \over F}\quad ,$$

where OCV_o is the stress free open circuit voltage.^{Reference Gibbs16} The current density at the groove can then be determined by combining Eqs. (11) and (12) as

(13)$$\left| i \right| = {{{V_{{\rm{applied}}}} - {\rm{OC}}{{\rm{V}}_{\rm{o}}} - {{A\Omega \left| p \right|} \over F}} \over {{R_{{\rm{BattA}}}}}}\quad ,$$

where for small defects (R ≤ ∼500 nm based on the results reported here and a previous publication),^{Reference Herbert, Hackney, Dudney, Thole and Phani3} the length scale may not allow glide-controlled dislocation mechanisms such as Frank–Reed sources to operate at stresses near the bulk yield strength. Under these conditions, dislocation plasticity will not be an efficient stress relief mechanism, allowing the hoop stress within the interfacial defect to build to values capable of initiating mode I fracture in the SE. In the absence of dislocation mediated plasticity, at very large gradients in stress (for small R), alternative stress relief mechanisms in Li may operate, particularly diffusional processes due to the large homologous temperature. A diffusional creep mechanism would be expected to operate at small R, as the gradient in chemical potential due to the hydrostatic stress gradient is proportional to 1/R. By analogy with Nabarro–Herring creep rate kinetics, the plastic strain rate term in Eq. (10) is expected to have the form

(14)$$\left| {{{\dot{\varepsilon }}_{{\rm{plastic}}}}} \right| = \left| {{{D\Omega } \over {{k_{\rm{B}}}T}}{p \over {{R^2}}}} \right|\quad .$$

Substituting Eqs. (13) and (14) into Eq. (10) yields a steady state (dp/dt = 0) hydrostatic stress magnitude given by

(15)$$\left| p \right| = {{2AF\left( {{V_{{\rm{applied}}}} - {\rm{OC}}{{\rm{V}}_{\rm{o}}}} \right)} \over {2{A^2}\Omega + \left( {D{R_{{\rm{BattA}}}}} \right){{{F^2}} \over {R{k_{\rm{B}}}T}}}}\quad .$$

It is noted with some satisfaction that the kinetic terms, D and R _BattA, are lumped together such that at D = 0, only the thermodynamic terms will determine p. It may also be seen that the geometric dependence (on R) is removed at D = 0. However, as the diffusion coefficient increases, the magnitude of p decreases and the positive correlation between the magnitude of p and R (proportional to the diffusion length) is emphasized. Due to the large thickness of the SE relative to the dimensions of the interfacial defect, the hoop stress acting at the Li/SE interface will be approximately equal in magnitude to p. We note the analogy of Eq. (15) with the nanoindentation results is that the high indentation strain rates correlate with a high current density and the length scale of the indentation corresponds to the length scale of the defect at the Li/SE interface. Based on the indentation results and the analysis here for high charging current densities, the high stresses at the Li/SE interface are expected when the length scale is large enough to inhibit diffusional relaxation, but not large enough to allow for the initiation of mobile glide dislocation multiplication.