Article contents
Monte Carlo simulations of magnetization state of ellipsoidal CoCu particles in disordered self-assembled arrays
Published online by Cambridge University Press: 03 May 2016
Abstract
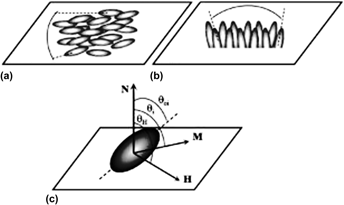
Monte Carlo (MC) simulations of the magnetization states of disordered self-assembled arrays of particles consisting of Co87Cu13 alloy are investigated. The assemblies of magnetic particles with ellipsoidal shapes and volumes ranging from 5 to 50 µm3 exhibit densities of about 3 × 106 particles per mm2. Magnetization was obtained in the framework of Stoner–Wohlfarth model extended to include phenomenological contributions of second-order magnetic anisotropy and coercivity mechanism with distinct configuration of easy axes of magnetization. MC simulations for assemblies containing no more than 100 particles with negligible magnetic interaction between each other and exhibiting saturation magnetization and magnetic anisotropy constant values close to those found for cobalt in bulk are in good agreement with experimental results. We evaluate and validate our computational modeling using samples having particles with different sizes and different angular distributions of the easy axis of magnetization. A simple numerical approach with minimum of parameters was used to take into account the coercive fields of the samples. Reasonable simulation results are generated based on realistic size distributions and angular distributions of easy axis of magnetization.
PACS numbers: 75.30.Gw,75.60-d,75.70-i
Keywords
- Type
- Articles
- Information
- Copyright
- Copyright © Materials Research Society 2016
Footnotes
Present address: Instituto de Física, Universidade Federal do Rio Grande do Sul, Av. Bento Gonçalves, 9500 – Caixa Postal 15051 – CEP 91501-970 – Porto Alegre, RS, Brazil.
Contributing Editor: Yang-T. Cheng
References
REFERENCES
- 1
- Cited by



