Hostname: page-component-8448b6f56d-mp689 Total loading time: 0 Render date: 2024-04-19T01:11:57.069Z Has data issue: false hasContentIssue false
  • English
  • Français

A model for the indentation size effect in polycrystalline alloys coupling intrinsic and extrinsic length scales

Published online by Cambridge University Press:  29 April 2019

Simon P.A. Gill  and
Christopher J. Campbell
Simon P.A. Gill*
Affiliation:
Department of Engineering, University of Leicester, Leicester LE1 7RH, U.K.
Christopher J. Campbell
Affiliation:
Department of Engineering, University of Leicester, Leicester LE1 7RH, U.K.
*
a)Address all correspondence to this author. e-mail: spg3@leicester.ac.uk
Get access

Abstract

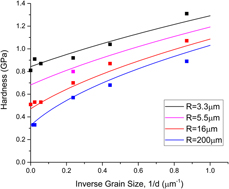
The measured hardness of a metal crystal depends on a variety of length scales. Microstructural features, such as grain size and precipitate spacing, determine the intrinsic material length scale. Extrinsic (test) length scales, such as the indentation depth, lead to the indentation size effect (ISE), whereby it is typically found that smaller is stronger. Nix and Gao [J. Mech. Phys. Solids46, 411 (1998)] developed a widely used model for interpreting the ISE based on forest hardening in single crystalline pure metals. This work extends that model to consider the hardness of polycrystals and alloys, as well as introducing a finite limit to the hardness at very small extrinsic length scales. The resulting expressions are validated against data from the literature. It is shown that a reasonable estimate of the intrinsic material length scale can be extracted from a suite of hardness tests conducted across a range of indentation depths using spherical indenters of various radii.

Keywords

microstructurehardnessstrength
Type
Article
Information
Journal of Materials Research , Volume 34 , Issue 10 , 28 May 2019 , pp. 1645 - 1653
Copyright
Copyright © Materials Research Society 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Greer, J.R. and De Hosson, J.T.M.: Plasticity in small-sized metallic systems: Intrinsic versus extrinsic size effect. Prog. Mater. Sci. 56, 654 (2011).CrossRefGoogle Scholar
Bushby, A.J. and Dunstan, D.J.: Plasticity size effects in nanoindentation. J. Mater. Res. 19, 137 (2003).CrossRefGoogle Scholar
Pharr, G.M. and Oliver, W.C.: Nanoindentation of silver-relations between hardness and dislocation structure. J. Mater. Res. 4, 94 (1988).CrossRefGoogle Scholar
Campbell, C.J. and Gill, S.P.A.: An analytical model for the flat punch indentation size effect. Int. J. Solids Struct. (2019). (in press).CrossRefGoogle Scholar
Nix, W.D. and Gao, H.: Indentation size effects in crystalline materials: A law for strain gradient plasticity. J. Mech. Phys. Solids 46, 411 (1998).CrossRefGoogle Scholar
Swadener, J.G., George, E.P., and Pharr, G.M.: The correlation of the indentation size effect measured with indenters of various shapes. J. Mech. Phys. Solids 50, 681 (2002).CrossRefGoogle Scholar
Pharr, G.M., Herbert, E.G., and Gao, Y.: The indentation size effect: A critical examination of experimental observations and mechanistic interpretations. Annu. Rev. Mater. Res. 40, 271 (2010).CrossRefGoogle Scholar
Ehrler, B., Dunstan, D.J., Zhu, T.T., Hou, X.D., P’ng, K.M.Y., and Bushby, A.J.: The strength of thin films, small structures and materials under localised stresses. Thin Solid Films 517, 3781 (2009).CrossRefGoogle Scholar
Gladman, T.: Precipitation hardening in metals. Mater. Sci. Technol. 15, 30 (1999).CrossRefGoogle Scholar
Morris, J.W.: Dislocation Plasticity: Overview (2018). Available at: http://www.mse.berkeley.edu/groups/morris/MSE205/Extras/dislocation%20plasticity.pdf (accessed December 13, 2018).Google Scholar
Zhu, T.T., Bushby, A.J., and Dunstan, D.J.: Materials mechanical size effects: A review. Mater. Technol. 23, 193 (2008).CrossRefGoogle Scholar
Ehrler, B., Hou, X.D., Zhu, T.T., P’ng, K.M.Y., Walker, C.J., Bushby, A.J., and Dunstan, D.J.: Grain size and sample size interact to determine strength in a soft metal. Philos. Mag. 88, 3043 (2008).CrossRefGoogle Scholar
Greer, J.R. and Nix, W.D.: Nanoscale gold pillars strengthened through dislocation starvation. Phys. Rev. B 73, 245410 (2006).CrossRefGoogle Scholar
Lefebvre, S., Devincre, B., and Hoc, T.: Simulation of the Hall–Petch effect in ultra-fine grained copper. Mater. Sci. Eng., A 400–401, 150 (2005).CrossRefGoogle Scholar
Dunstan, D.J., Ehrler, B., Bossis, R., Joly, S., P’ng, K.M.Y., and Bushby, A.J.: Elastic limit and strain hardening of thin wires in torsion. Phys. Rev. Lett. 103, 155501 (2009).CrossRefGoogle ScholarPubMed
Jones, D.R. and Ashby, M.F.: Engineering Materials 1: An Introduction to Properties, Applications and Design (Elsevier, Oxford, England, 2011).Google Scholar
Labusch, R.: A statistical theory of solid solution hardening. Phys. Status Solidi B 41, 659 (1970).CrossRefGoogle Scholar
Atkinson, H. and Gill, S.: Modelling creep in nickel alloys in high temperature power plants. In Structural Alloys for Power Plants, Shirzadi, A. and Jackson, S., eds. (Elsevier, Cambridge, U.K., 2014); p. 447.CrossRefGoogle Scholar
Queyreau, S., Monnet, G., and Devincre, B.: Orowan strengthening and forest hardening superposition examined by dislocation dynamics simulations. Acta Mater. 58, 5586 (2010).CrossRefGoogle Scholar
Rester, M., Motz, C., and Pippan, R.: Where are the geometrically necessary dislocations accommodating small imprints? J. Mater. Res. 24, 647 (2008).CrossRefGoogle Scholar
Durst, K., Backes, B., and Göken, M.: Indentation size effect in metallic materials: Correcting for the size of the plastic zone. Scr. Mater. 52, 1093 (2005).CrossRefGoogle Scholar
Huang, Y., Zhang, F., Hwang, K.C., Nix, W.D., Pharr, G.M., and Feng, G.: A model of size effects in nano-indentation. J. Mech. Phys. Solids 54, 1668 (2006).CrossRefGoogle Scholar
McElhaney, K.W., Vlassak, J.J., and Nix, W.D.: Determination of indenter tip geometry and indentation contact area for depth-sensing indentation experiments. J. Mater. Res. 13, 1300 (1997).CrossRefGoogle Scholar
Sousa, T.G.d., Sordi, V.L., and Brandão, L.P.: Dislocation density and texture in copper deformed by cold rolling and ecap. Mater. Res. 21 (2018).Google Scholar
Feng, G. and Nix, W.D.: Indentation size effect in MgO. Scr. Mater. 51, 599 (2004).CrossRefGoogle Scholar
Hou, X.D., Bushby, A.J., and Jennett, N.M.: Study of the interaction between the indentation size effect and Hall–Petch effect with spherical indenters on annealed polycrystalline copper. J. Phys. D: Appl. Phys. 41, 074006 (2008).CrossRefGoogle Scholar