I. INTRODUCTION
Indentation of polymeric or biological materials or their composites frequently leads to three concurrent modes of contact deformation, characterized by three different variations of the indenter displacement into the material, h, with indentation load, P, and time, t Reference Oyen and Cook1–Reference Isaza, Mazeran, El Kirat and Ho Ba Tho12 :
-
(V) Viscous deformation, in which the indenter displacement is time-dependent, typically with the rate of displacement varying with load.
-
(E) Elastic deformation, in which the indenter displacement is time-independent and recovers completely on load removal.
-
(P) Plastic deformation, in which the indenter displacement is time-independent and does not recover at all on load removal.
Indentation with a spherical probe or flat punch often suppresses plastic deformation such that the deformation is completely viscoelastic, Reference Oyen and Cook6,Reference Rodriguez-Florez, Oyen and Shefelbine11,Reference Cheng, Xia, Yu, Scriven and Gerberich13–Reference Oyen20 or is assumed so for fluid-like materials. Reference Sakai and Shimizu14,Reference Sakai15,Reference Shimizu, Yanagimoto and Sakai21,Reference Sakai, Shimizu, Miyajima, Tanabe and Yasuda22 Under these conditions, viscoelastic correspondence principles Reference Lee and Radok23–Reference Ting27 can be used to predict the h(t) response from an imposed P(t) spectrum (or vice versa) if the purely elastic P(h) indentation behavior is known and a time-dependent creep (or relaxation) function is selected for the material. The predictions are frequently framed in terms of superposition integrals. Indentation with the more-commonly used pyramidal probes, such as the three-sided Berkovich diamond, usually generates all three of the viscous-elastic-plastic (VEP) indentation deformations. Under these conditions, correspondence principles, which rely on material linearity in elastic and viscous constitutive behavior (Hookean and Newtonian, respectively), cannot be used as the plasticity renders the nonviscous component of the deformation nonlinear. Hence, although correspondence methods can incorporate the geometrical nonlinearity of spherical and pyramidal indentation, in which the indentation contact area increases with indentation depth, Reference Graham25 plastic deformation precludes their use.
The original VEP indentation model incorporated the geometrical nonlinearity of pyramidal indentation explicitly into each component of the deformation, Reference Oyen and Cook1 treating each displacement component separately. The plastic displacement, h P(t), was given by
where P max(t) is the maximum load experienced over the time interval t, α1 is a dimensionless indenter geometry constant, and H is the resistance to plastic deformation. For an elastic-perfectly plastic material H is the hardness. The elastic displacement, h E(t), was given by
where α2 is another dimensionless indenter geometry constant, and M is the resistance to elastic deformation. For an elastic material, M is the indentation modulus. The viscous displacement, h V(t), was expressed as a rate,
where τ is the time constant for viscous flow. The term α2 Mτ2 is an effective quadratic viscosity. [Eqs. (2) and (3) use the more recent notation. Reference Cook and Oyen4 ] The total indentation displacement was taken as the sum
such that the overall indentation model could be viewed as a generalized quadratic “Maxwell”-like model of elements in series. For simple loading schemes, such as triangular, linear load-unload, spectra, the integral implicit in Eq. (3) is simply performed and the total displacement given by Eq. (4) can be expressed in closed form. The simplicity of this formulation allows the resistance to the three different modes of deformation to be scaled separately via H, M, and τ, such that the complete variety of material indentation load–displacement responses can be described and analyzed. Reference Cook and Oyen4,Reference Oyen and Cook6
The quadratic Maxwell VEP model above was reasonably successful in a quantitative sense: the material properties H, M, and τ inferred from fits of the model to triangular load spectra, specifically fits to the unloading response in which all three displacement components are distinct, were in agreement with other measurements Reference Oyen and Cook1,Reference Oyen, Cook, Emerson and Moody2,Reference Oyen and Ko5 ; the ability of the model to predict loading behavior from unloading behavior was excellent Reference Oyen and Cook1,Reference Oyen, Cook, Emerson and Moody2,Reference Cook and Oyen4,Reference Oyen and Ko5,Reference Wang and Lloyd8 ; and the material properties inferred using a triangular load spectrum at a reference time- or load-scale could be used to predict the triangular responses for indentation time scales factors of three shorter or longer than the reference and indention load-scales factors of ten different from the references. Reference Oyen and Cook1,Reference Oyen, Cook, Emerson and Moody2,Reference Cook and Oyen4,Reference Wang and Lloyd8 The limitations of the quadratic Maxwell VEP model are apparent in comparisons of observed and predicted behavior during constant-load creep, a test method that focuses on the time-dependent constitutive behavior. The free viscous element, meaning that it has no element constraining it in parallel, of the quadratic Maxwell VEP model leads to unbounded displacement increasing linearly with time for an imposed constant load and an instantaneous displacement recovery on load removal. Reference Oyen and Cook1 Neither of these phenomena are observed during indentation of the vast majority of polymeric and biological materials: Displacement rates during constant-load creep decrease with time such that the displacement approaches a bounded value at long times Reference Oyen and Cook1,Reference Zhang, Zhang, Zeng and Shen3,Reference Olesiak, Oyen and Ferguson7,Reference Mazeran, Beyaoui, Bigerelle and Guigon9,Reference Rodriguez-Florez, Oyen and Shefelbine11,Reference Isaza, Mazeran, El Kirat and Ho Ba Tho12,Reference Oyen20 and recovery on load removal is not instantaneous but occurs over time scales comparable to those required to reach the bounded creep displacement. Reference Mazeran, Beyaoui, Bigerelle and Guigon9,Reference Isaza, Mazeran, El Kirat and Ho Ba Tho12 Furthermore, the time-dependent indentation creep and recovery behavior of most polymeric and biological materials is not well described by a single-time-constant, but by two or more. Reference Zhang, Zhang, Zeng and Shen3,Reference Mazeran, Beyaoui, Bigerelle and Guigon9,Reference Isaza, Mazeran, El Kirat and Ho Ba Tho12,Reference Yang, Zhang and Zeng16,Reference Oyen18–Reference Oyen20
Here, a new VEP pyramidal indentation model and analysis is developed that is similar in spirit to the original model (elements in series, closed-form displacement expressions, simple identification of material behavior dependencies) but which overcomes the deficiencies noted above. As foreshadowed earlier, Reference Cook and Oyen4 the model is based on a quadratic “Kelvin”-like element, in which the viscous element is bounded by an elastic element in parallel, such that displacement during constant-load creep is bounded and displacement recovery on load removal is not instantaneous. Two such viscoelastic elements are combined in series to provide for deformation over two time scales, along with a third, plastic, element in series as before. A schematic diagram of the full quadratic Kelvin VEP model is shown in Fig. 1. The model is nearly identical to that recently implemented by Mazeran et al. Reference Mazeran, Beyaoui, Bigerelle and Guigon9 and Isaza et al., Reference Isaza, Mazeran, El Kirat and Ho Ba Tho12 with the omission of the fourth quadratic Maxwell element used by Mazeran, Isaza et al. to describe a viscoplastic response. In the original VEP model, the behavior of the single-time-constant viscous element could be deconvoluted unambiguously from the indentation unloading response of a simple load triangle. The extra degree of freedom associated with the two time constants of the two viscoelastic elements in Fig. 1 precludes such simple deconvolution and a more extensive testing protocol is required. Here, a three-segment load spectrum is used as shown in Fig. 2(a): (i) a triangle wave, followed by (ii) a near-zero load hold, followed by (iii) a trapezoidal load wave. The protocol is identical to that used by Zhang et al. Reference Zhang, Zhang, Zeng and Shen3 for exactly the same reasons: the final trapezoidal segment isolates the viscoelastic response under constant-load conditions that are simple to analyze.

FIG. 1. Schematic diagram of the pyramidal indentation quadratic Kelvin VEP model. The model consists of two quadratic viscoelastic Kelvin elements in series with a quadratic plastic element.

FIG. 2. Experimental load–displacement–time, P–h–t, data for the PMMA1 material during the three-segment indentation test. (a) The imposed triangle-hold-trapezoid load spectrum; the end of the initial triangle to peak load P T and the beginning of the creep segment at load P R of the final trapezoid are indicated by vertical lines. (b) The resulting displacement response; at the end of the central hold the displacement is h PT. (c) The displacement in the creep segment of the final trapezoid in shifted coordinates.
A major motivation for the development of the new model and analysis was to map the mechanical properties of polymer-carbon nanotube (CNT) composites. Such composites have great potential as lightweight mechanical or electrical materials that take advantage of the high stiffness and strength or electrical conductivity of CNTs, respectively. As with all composites, appropriate dispersion of the minority enhancing phase in the majority matrix phase is critical to obtaining desired properties: For example, the stiff CNTs must be dispersed and bound to the compliant polymer matrix so as to achieve stress transfer and stiffening of the composite; the conducting CNTs must be dispersed so as to percolate throughout the insulating polymer matrix so as to obtain a conducting structure. As a consequence, considerations of CNT dispersion in polymer matrices have been the subject of much study since the early applications of CNTs. Reference Sandler, Shaffer, Prasse, Bauhofer, Schulte and Windle28–Reference Chakraborty, Plyhm, Barbezat, Necola and Terrasi31
The goal here was to develop an instrumented indentation testing (IIT) method that could provide a direct measure of the mechanical behavior of polymer-CNT composites in the form of two-dimensional maps of viscoelastic and plastic properties. Such maps take advantage of the local probing capabilities of IIT and have been used to explore the effects of microstructure on spatial variations of mechanical properties in ceramic-metal composites, Reference Engqvist and Wiklund32 tooth enamel, Reference Cuy, Mann, Livi, Teaford and Weihs33 bone, Reference Gupta, Stachewicz, Wagermaier, Roschger, Wagner and Fratzl34 cement paste and rocks, Reference Zhu, Hughes, Bicanic and Pearce35 and metals. Reference Randall, Vandamme and Ulm36,Reference Goldbaum, Chromik, Brodusch and Gauvin37 In these cases, time-dependent deformation was not considered and elastic and plastic properties were mapped. The next section develops the new VEP indentation model and expressions for h(t) that allow material properties to be determined from simple P(t) protocols. The following sections then demonstrate and validate the applicability of the model in single-point tests on monolithic polymers and glass. The mapping capability is then demonstrated in multipoint tests on a ceramic–polymer interface and two polymer–CNT composites. Finally, possible extensions of the model and protocols are discussed.
II. MATERIALS AND METHODS
A. Materials
Five common commercial polymeric materials were obtained in approximately 1 mm thick solid sheet form. The materials were a high-density polyethylene (HDPE), two poly(methyl methacrylate)s (PMMA1, and PMMA2), a polystyrene (PS), and a polycarbonate (PC). Samples approximately 15 mm × 15 mm were cut from the sheets and fixed to aluminum pucks for IIT measurements. The surfaces of the samples were highly reflective and tested in the as-received state, except for the HDPE, which was diamond polished to a reflective state. A commercial soda-lime silicate glass (SLG) microscope slide was also tested.
Two commercial epoxy materials were obtained in liquid form as separate resins and curing agents. The first (Epoxy1) consisted of Epon 828 resin (miller–stephenson, Danbury, CT) and Ancamide 507 curing agent (Air Products, Allentown, PA). The resin and curing agent were mixed in the proportion 3:1 by mass and samples approximately 5 mm thick cast into circular plastic molds 35 mm in diameter, allowed to cure at room temperature for 48 h, and then removed from the molds. The surfaces cast against the base of the molds were highly reflective and tested in the as-cast state. The second (Epoxy2) consisted of a resin and curing agent used for metallographic sample preparation, mixed as directed by the supplier (Buehler, Lake Bluff, IL), cast into a circular plastic mold along with a piece of dense aluminum nitride (AlN) ceramic, and allowed to cure as directed. The composite sample was removed from the mold and diamond polished to a reflective state such that a sharp epoxy-ceramic interface was normal to the sample surface.
Two epoxy-CNT composite materials were obtained from a commercial vendor. The composites consisted of mass fractions of 1% and 5% of multiwall CNT (MWCNT) mixed into an epoxy matrix equivalent to Epoxy1 above. To enable direct comparison with the mechanical properties of the matrix epoxy, no chemical additives to improve homogeneity of MWCNT dispersion were included in the composites; it was thus expected that the MWCNT dispersion would be somewhat inhomogeneous. Reference Xie, Mai and Zhou29,Reference Ma, Siddiqui, Marom and Kim30 The composite material samples were in the form of 15 mm × 15 mm sheets approximately 0.5 mm thick and were fixed to aluminum pucks with Epoxy1 for IIT measurements. The surfaces of the samples were reflective and tested in the as-received state.
B. Experimental methods
Single-point IIT measurements of the monolithic materials were used to establish and validate the experimental and analytical methods in two sequential stages. In the first stage, indentation displacements were measured during a three-segment applied load spectrum as described above. Material properties were determined from these measurements. In the second stage, indentation displacements were predicted from these properties for a range of single-segment linear load ramps and compared with experimental measurements; the property values were also compared with accepted values for the materials. In this way, the validity of both the form of the analysis and the magnitude of the included parameters could be assessed. A Berkovich diamond probe was used for all experiments. The data collection rate for load, displacement, and time for all experiments was at least 10 Hz.
The first-stage, three-segment applied load spectrum was as follows:
-
(i) A triangular segment, consisting of a linear load ramp from zero to a peak load of P T and then a linear ramp back to near zero over a total period of approximately 30 s; the end of this segment is indicated by the left vertical line in Fig. 2. P T = 100 mN was used. The displacement response for PMMA1 is shown in Fig. 2(b) and consisted of an increase from zero to a peak displacement followed by a decrease to a nonzero displacement at the end of the segment.
-
(ii) A period of near zero load, approximately 1 mN, typically extending for 600 s. The displacement response for PMMA1 is shown in Fig. 2(b) and consisted of recovery to a near invariant displacement, h PT, at the end of the segment.
-
(iii) A trapezoidal segment consisting of a linear ramp from near zero load to peak load of P R < P T in a time of t R, a long creep load-hold period at P R, and a linear ramp to zero load. P R = 60 mN and t R ≈ 10 s were used and the creep hold period was typically 1000 s; the beginning of the creep hold period is indicated by the right vertical line in Fig. 2. The displacement response for PMMA1 is shown in Fig. 2(b) and consisted of a rapid increase in displacement followed by a slower increase to near invariant displacement at the end of the creep hold. An expanded view of the slower creep displacement response is shown in shifted creep coordinates in Fig. 2(c) (setting the creep time to 0 after the t R ≈ 10 s rise to the creep load); analysis of such data provided the majority of the material viscoelastic information. At least four three-segment spectra were measured and analyzed for each material. Prior to measurement, preliminary trapezoidal experiments were used to ascertain the characteristic time scales for deformation.
The second-stage validation experiments were a series of linear load ramps. The ramps were part of a triangular load wave as illustrated in the initial segment of Fig. 1(a), with the exceptions that the peak loads were variable values P U and the rise times were much longer variable values t U. (The subscript “U” indicates that these validation conditions are in principle unknown during the above first-stage measurements.) Only the loading parts of the triangle waves were used in the validation experiments. Two different forms of validation experiments were performed on PMMA1: (i) loading to a fixed peak load of P U = 100 mN with variable rise times of t U = (20, 50, 100, 200, 500, 1000, and 2000) s; and, (ii) loading with fixed rise time of t U = 500 s and variable peak loads of P U = (20, 50, 100, 200, and 500) mN. A single form of validation experiment was performed on the set of monolithic materials: loading with a fixed rise time of t U = 1000 s to a peak load of P U = 100 mN or P U = 50 mN (HDPE only).
Multipoint measurements of the epoxy-ceramic interface and the epoxy-CNT composites were used to generate line scans and maps of viscoelastic and plastic deformation properties. Linear arrays of 10 indentations on 100 µm centers were performed over randomly selected areas of the composites for direct quantitative comparisons of properties with the base epoxy. A two-dimensional 10 × 10 array of indentations was performed over a 900 µm × 900 µm square centered on the interface in the epoxy-ceramic sample to demonstrate the mapping capability in an extreme case of spatial property variation. Similar arrays of indentations were performed on randomly selected areas of the epoxy-CNT composites to demonstrate the mapping capability in inhomogeneous polymer microstructures. The three-segment test sequence described above was used for all the multipoint measurements; the total test time for the two-dimensional arrays was nearly 48 h.
C. Analysis method
The analytical method developed here will be used to extract material mechanical properties from displacement measurements during the three-segment experimental applied load spectrum. The total indentation displacement at all times is given by the sum of the plastic and viscoelastic displacements, truncating Eq. (3) to
where the viscoelastic displacement, h VE, is now given by the sum of the displacements of two quadratic Kelvin elements in series, Fig. 1,
The plastic displacement is as before, Eq. (1). The displacement for each quadratic Kelvin element is described by a differential equation [see Appendix, Eq. (A4)],
where i = 1 or 2, and (for each element) M i is the viscoelastic resistance, and τ i is the time constant for viscoelastic deformation. [In the limit of τ i >> dt/dln h VEi , Eq. (6) reverts to the form of Eq. (3).]
At the end of the triangular segment (i), the displacement consists of the sum of plastic deformation given by Eq. (1) and viscoelastic deformation given by an expression similar to Eqs. (A10a) and (A10b), but the relative proportions are not known. At the end of the recovery segment (ii), the viscoelastic deformation has decayed to near zero, if the segment is long enough, similar to Eq. (A11), such that only displacement associated with plastic deformation remains:
The “T” subscript in h PT indicates that the plastic displacement is set by the maximum load attained, P T (Fig. 2) and remains invariant thereafter. Equation (7) allows α1 H to be determined for the material from the measured values of h PT and P T.
As P R < P T in the trapezoidal segment (iii), there is no further plastic deformation and the additional displacement is completely viscoelastic and described by an expression similar to Eq. (A9). In particular, during the hold of the trapezoidal segment, the viscoelastic displacement is given by solving the differential equation for each quadratic Kelvin element for fixed load to gain
 $$\eqalign{ {h_{{\rm{VE}}}} = {h_{\rm{R}}} + & \left[ {{{\left( {{{{P_{\rm{R}}}} \over {{\alpha _2}{M_1}}}} \right)}^{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}} - {h_{{\rm{R1}}}}} \right]\left[ {1 - \exp \left( { - {{\left( {t - {t_{\rm{R}}}} \right)} \over {{\tau _1}}}} \right)} \right] \cr + & \left[ {{{\left( {{{{P_{\rm{R}}}} \over {{\alpha _2}{M_2}}}} \right)}^{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}} - {h_{{\rm{R2}}}}} \right]\left[ {1 - \exp \left( { - {{\left( {t - {t_{\rm{R}}}} \right)} \over {{\tau _2}}}} \right)} \right]\quad . \cr}$$
$$\eqalign{ {h_{{\rm{VE}}}} = {h_{\rm{R}}} + & \left[ {{{\left( {{{{P_{\rm{R}}}} \over {{\alpha _2}{M_1}}}} \right)}^{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}} - {h_{{\rm{R1}}}}} \right]\left[ {1 - \exp \left( { - {{\left( {t - {t_{\rm{R}}}} \right)} \over {{\tau _1}}}} \right)} \right] \cr + & \left[ {{{\left( {{{{P_{\rm{R}}}} \over {{\alpha _2}{M_2}}}} \right)}^{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}} - {h_{{\rm{R2}}}}} \right]\left[ {1 - \exp \left( { - {{\left( {t - {t_{\rm{R}}}} \right)} \over {{\tau _2}}}} \right)} \right]\quad . \cr}$$
h R is the total displacement at the end of the ramp of the trapezoidal segment, and thus the displacement at the beginning of the hold segment; h R1 and h R2 are the contributions of each viscoelastic element to the total, h R = h R1 + h R2. Fitting Eq. (8) to the measured h VE(t) response enables the time constants τ1 and τ2 to be determined, along with the amplitudes characterizing each exponential term. An example fit for PMMA1 is shown in Fig. 2(c), using the natural creep coordinates from Eq. (8) of t – t R and h VE – h R. During the ramp of the trapezoidal segment, the viscoelastic displacement is given by solving the differential equation for each quadratic Kelvin element for linearly increasing load, such that at peak ramp load, P R, the displacement h R is given by
 $$\eqalign{ {h_{\rm{R}}} = {\left( {{{{P_{\rm{R}}}} \over {{\alpha _2}{M_1}}}} \right)^{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}} & \left[ {1 - {{\sqrt \pi } \over 2}{{\left( {{{{\tau _1}} \mathord{\left/ {\vphantom {{{\tau _1}} {{t_{\rm{R}}}}}} \right. \kern-\nulldelimiterspace} {{t_{\rm{R}}}}}} \right)}^{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}}\exp \left( {{{ - {t_{\rm{R}}}} \mathord{\left/ {\vphantom {{ - {t_{\rm{R}}}} {{\tau _1}}}} \right. \kern-\nulldelimiterspace} {{\tau _1}}}} \right){\rm{erf}}{{\left( {{{{t_{\rm{R}}}} \mathord{\left/ {\vphantom {{{t_{\rm{R}}}} {{\tau _1}}}} \right. \kern-\nulldelimiterspace} {{\tau _1}}}} \right)}^{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}}} \right] \cr + & {\left( {{{{P_{\rm{R}}}} \over {{\alpha _2}{M_2}}}} \right)^{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}}\left[ {1 - {{\sqrt \pi } \over 2}{{\left( {{{{\tau _2}} \mathord{\left/ {\vphantom {{{\tau _2}} {{t_{\rm{R}}}}}} \right. \kern-\nulldelimiterspace} {{t_{\rm{R}}}}}} \right)}^{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}}\exp \left( {{{ - {t_{\rm{R}}}} \mathord{\left/ {\vphantom {{ - {t_{\rm{R}}}} {{\tau _2}}}} \right. \kern-\nulldelimiterspace} {{\tau _2}}}} \right){\rm{erf}}{{\left( {{{{t_{\rm{R}}}} \mathord{\left/ {\vphantom {{{t_{\rm{R}}}} {{\tau _2}}}} \right. \kern-\nulldelimiterspace} {{\tau _2}}}} \right)}^{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}}} \right]\quad . \cr}$$
$$\eqalign{ {h_{\rm{R}}} = {\left( {{{{P_{\rm{R}}}} \over {{\alpha _2}{M_1}}}} \right)^{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}} & \left[ {1 - {{\sqrt \pi } \over 2}{{\left( {{{{\tau _1}} \mathord{\left/ {\vphantom {{{\tau _1}} {{t_{\rm{R}}}}}} \right. \kern-\nulldelimiterspace} {{t_{\rm{R}}}}}} \right)}^{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}}\exp \left( {{{ - {t_{\rm{R}}}} \mathord{\left/ {\vphantom {{ - {t_{\rm{R}}}} {{\tau _1}}}} \right. \kern-\nulldelimiterspace} {{\tau _1}}}} \right){\rm{erf}}{{\left( {{{{t_{\rm{R}}}} \mathord{\left/ {\vphantom {{{t_{\rm{R}}}} {{\tau _1}}}} \right. \kern-\nulldelimiterspace} {{\tau _1}}}} \right)}^{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}}} \right] \cr + & {\left( {{{{P_{\rm{R}}}} \over {{\alpha _2}{M_2}}}} \right)^{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}}\left[ {1 - {{\sqrt \pi } \over 2}{{\left( {{{{\tau _2}} \mathord{\left/ {\vphantom {{{\tau _2}} {{t_{\rm{R}}}}}} \right. \kern-\nulldelimiterspace} {{t_{\rm{R}}}}}} \right)}^{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}}\exp \left( {{{ - {t_{\rm{R}}}} \mathord{\left/ {\vphantom {{ - {t_{\rm{R}}}} {{\tau _2}}}} \right. \kern-\nulldelimiterspace} {{\tau _2}}}} \right){\rm{erf}}{{\left( {{{{t_{\rm{R}}}} \mathord{\left/ {\vphantom {{{t_{\rm{R}}}} {{\tau _2}}}} \right. \kern-\nulldelimiterspace} {{\tau _2}}}} \right)}^{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}}} \right]\quad . \cr}$$
Combining Eqs. (8) and (9) allows the contributions to the amplitude terms, α2 M 1 and α2 M 2 and h R1 and h R2, to be separated and determined for the material from the measured values of h R, P R, and t R.
Once the material parameters are determined, it is then possible to predict the load–displacement–time response for an arbitrary load spectrum. Comparison of such predictions with measured responses is a test of the range of validity of the parameters and of the model. Here, for simplicity, the material parameters are used to predict the response to a linear load ramp to peak load P U in time t U. The full displacement response is given by
 $$\eqalign{ h\left( t \right) = {\left( {{{{P_{\rm{U}}}t} \mathord{\left/ {\vphantom {{{P_{\rm{U}}}t} {{t_{\rm{U}}}{\alpha _1}H}}} \right. \kern-\nulldelimiterspace} {{t_{\rm{U}}}{\alpha _1}H}}} \right)^{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}} \,+\, & {\left( {{{{P_{\rm{U}}}} \over {{\alpha _2}{M_1}}}} \right)^{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}}\left[ {{{\left( {{t \mathord{\left/ {\vphantom {t {{t_{\rm{U}}}}}} \right. \kern-\nulldelimiterspace} {{t_{\rm{U}}}}}} \right)}^{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}} - {{\sqrt \pi } \over 2}{{\left( {{{{\tau _1}} \mathord{\left/ {\vphantom {{{\tau _1}} {{t_{\rm{U}}}}}} \right. \kern-\nulldelimiterspace} {{t_{\rm{U}}}}}} \right)}^{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}}\exp \left( {{{ - t} \mathord{\left/ {\vphantom {{ - t} {{\tau _1}}}} \right. \kern-\nulldelimiterspace} {{\tau _1}}}} \right){\rm{erf}}{{\left( {{t \mathord{\left/ {\vphantom {t {{\tau _1}}}} \right. \kern-\nulldelimiterspace} {{\tau _1}}}} \right)}^{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}}} \right] \cr \,+\, & {\left( {{{{P_{\rm{U}}}} \over {{\alpha _2}{M_2}}}} \right)^{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}}\left[ {{{\left( {{t \mathord{\left/ {\vphantom {t {{t_{\rm{U}}}}}} \right. \kern-\nulldelimiterspace} {{t_{\rm{U}}}}}} \right)}^{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}} - {{\sqrt \pi } \over 2}{{\left( {{{{\tau _2}} \mathord{\left/ {\vphantom {{{\tau _2}} {{t_{\rm{U}}}}}} \right. \kern-\nulldelimiterspace} {{t_{\rm{U}}}}}} \right)}^{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}}\exp \left( {{{ - t} \mathord{\left/ {\vphantom {{ - t} {{\tau _2}}}} \right. \kern-\nulldelimiterspace} {{\tau _2}}}} \right){\rm{erf}}{{\left( {{t \mathord{\left/ {\vphantom {t {{\tau _2}}}} \right. \kern-\nulldelimiterspace} {{\tau _2}}}} \right)}^{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}}} \right]\quad . \cr}$$
$$\eqalign{ h\left( t \right) = {\left( {{{{P_{\rm{U}}}t} \mathord{\left/ {\vphantom {{{P_{\rm{U}}}t} {{t_{\rm{U}}}{\alpha _1}H}}} \right. \kern-\nulldelimiterspace} {{t_{\rm{U}}}{\alpha _1}H}}} \right)^{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}} \,+\, & {\left( {{{{P_{\rm{U}}}} \over {{\alpha _2}{M_1}}}} \right)^{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}}\left[ {{{\left( {{t \mathord{\left/ {\vphantom {t {{t_{\rm{U}}}}}} \right. \kern-\nulldelimiterspace} {{t_{\rm{U}}}}}} \right)}^{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}} - {{\sqrt \pi } \over 2}{{\left( {{{{\tau _1}} \mathord{\left/ {\vphantom {{{\tau _1}} {{t_{\rm{U}}}}}} \right. \kern-\nulldelimiterspace} {{t_{\rm{U}}}}}} \right)}^{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}}\exp \left( {{{ - t} \mathord{\left/ {\vphantom {{ - t} {{\tau _1}}}} \right. \kern-\nulldelimiterspace} {{\tau _1}}}} \right){\rm{erf}}{{\left( {{t \mathord{\left/ {\vphantom {t {{\tau _1}}}} \right. \kern-\nulldelimiterspace} {{\tau _1}}}} \right)}^{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}}} \right] \cr \,+\, & {\left( {{{{P_{\rm{U}}}} \over {{\alpha _2}{M_2}}}} \right)^{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}}\left[ {{{\left( {{t \mathord{\left/ {\vphantom {t {{t_{\rm{U}}}}}} \right. \kern-\nulldelimiterspace} {{t_{\rm{U}}}}}} \right)}^{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}} - {{\sqrt \pi } \over 2}{{\left( {{{{\tau _2}} \mathord{\left/ {\vphantom {{{\tau _2}} {{t_{\rm{U}}}}}} \right. \kern-\nulldelimiterspace} {{t_{\rm{U}}}}}} \right)}^{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}}\exp \left( {{{ - t} \mathord{\left/ {\vphantom {{ - t} {{\tau _2}}}} \right. \kern-\nulldelimiterspace} {{\tau _2}}}} \right){\rm{erf}}{{\left( {{t \mathord{\left/ {\vphantom {t {{\tau _2}}}} \right. \kern-\nulldelimiterspace} {{\tau _2}}}} \right)}^{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}}} \right]\quad . \cr}$$
In practice, it was more convenient to carry out the fitting and prediction in the normalized coordinates of t/t R, h/h R, and P/P R referenced to the parameters characterizing the ramp at the beginning of the trapezoidal segment (iii). Equations (8)–(10) then took on simpler forms and the normalized loads and displacements were of order unity, greatly simplifying fitting. More importantly, on normalization α2 M 1 and α2 M 2 were then determined as explicit fitting parameters from Eqs. (8) and (9). This determination enabled predictions from Eq. (10) to be expressed entirely in terms of the dimensionless experimental ratios t U/t R and P U/P R without recourse to explicit specification of the geometry terms α1 and α2 and thus of the material properties H, M 1, and M 2.
III. RESULTS
A. Model validation via single-point measurements
Experimental displacement measurements for the PMMA1 material, such as shown in Figs. 2(b) and 2(c), gave parameters of α1 H = (33.3 ± 0.4) GPa, α2 M 1 = (13.4 ± 0.1) GPa, α2 M 2 = (470 ± 8) GPa, τ1 = (23.0 ± 0.4) s, and τ2 = (547 ± 14) s, where the values represent the means and standard deviations of best fits to Eqs. (7)–(9) from four separate three-segment indentation experiments. Here and throughout, (τ1, M 1) are taken to characterize the faster, short time constant viscoelastic deformation process and (τ2, M 2) the slower, long time constant process. Figure 3 shows as symbols the load–displacement behavior of the PMMA1 material during linear load ramps to 100 mN with rises times from 20 s to 2000 s. (For clarity, as in Figs. 2, 4 and 5, the data are offset and not every measurement is shown.) Inspection of Fig. 3 shows that the displacement at peak load increased from about 4000 nm for a rise time of 20 s to about 5000 nm for a rise time of 2000 s, indicative of greater viscous flow as the test duration increased over this time scale. The solid lines in Fig. 3 are predictions of the load–displacement responses using Eq. (10) and the parameters given above. For rise times comparable to the creep hold time used to determine the viscoelastic parameters, 1000 s, the predictions are a very good fit to the measurements. These fits reflect the fact that the 1000 s hold was easily able to capture the viscoelastic deformation processes associated with the longer τ2 time constant, ≈ 500 s [see Fig. 2(c)]. As the rise times decrease, the predictions do not fit the measurements as well, particularly in the early part of the experiments. These observations serve to place bounds on the validity of the model, consistent with the idea that events shorter than about two or three time constants for a modeled process will not be well described. In this case, the shorter τ1 time constant places an upper bound on the time scale for events to be well described of ≈ (40–60) s, in agreement with Fig. 3. The obvious remedy, at the cost of model complexity, is to increase the number of viscoelastic elements and time constants. Reference Yang, Zhang and Zeng16,Reference Oyen18–Reference Oyen20,Reference Findley, Lai and Onaran38 As the inferred properties and resulting maps here used measurements deliberately not affected by the extreme short rise times used for illustration in Fig. 3, additional elements were not needed in this study.

FIG. 3. Load–displacement responses of the PMMA1 material during linear load-time indentation ramps to the same peak load, but different rise times, t U. Symbols indicate experimental observations (not all shown) and the lines indicate predictions from measurements and analyses of three segment (Fig. 2) tests. Data offset horizontally for clarity.

FIG. 4. Load–displacement responses of the PMMA1 material during linear load-time indentation ramps with the same rise time, but different peak loads. Symbols indicate experimental observations (not all shown) and the lines indicate predictions from measurements and analyses of three segment (Fig. 2) tests. Data offset horizontally for clarity.

FIG. 5. Load–displacement responses of silicate glass and polymer materials during linear load-time indentation ramps. Symbols indicate experimental observations (not all shown) and the lines indicate predictions from measurements and analyses of three segment (Fig. 2) tests. Data offset horizontally for clarity.
Figure 4 shows as symbols the load–displacement behavior of the PMMA1 material during linear load ramps to (20–500) mN with a rise time of 500 s. The solid lines in Fig. 4 are predictions of the load–displacement responses using Eq. (10) and the parameters given above. In distinction to Fig. 3, the predictions are a very good fit to the measurements for all the peak loads. This latter observation is a consequence of the fact that the relative contributions to total deformation from plastic and viscoelastic processes remain fixed if the rise time is fixed even as the peak load (and hence loading rate) changes [Eqs. (9) and (10)]. Inserting t = t U into Eq. (10) gives the displacement h U at peak load of a ramp:
 $${h_{\rm{U}}} = {\left( {{{{P_{\rm{U}}}} \mathord{\left/ {\vphantom {{{P_{\rm{U}}}} {{\alpha _1}H}}} \right. \kern-\nulldelimiterspace} {{\alpha _1}H}}} \right)^{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}} + {\left( {{{{P_{\rm{U}}}} \mathord{\left/ {\vphantom {{{P_{\rm{U}}}} {{\alpha _2}{M_{\rm{1}}}}}} \right. \kern-\nulldelimiterspace} {{\alpha _2}{M_{\rm{1}}}}}} \right)^{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}}\left[ {1 - f\left( {{{{\tau _1}} \mathord{\left/ {\vphantom {{{\tau _1}} {{t_{\rm{U}}}}}} \right. \kern-\nulldelimiterspace} {{t_{\rm{U}}}}}} \right)} \right] + {\left( {{{{P_{\rm{U}}}} \mathord{\left/ {\vphantom {{{P_{\rm{U}}}} {{\alpha _2}{M_{\rm{2}}}}}} \right. \kern-\nulldelimiterspace} {{\alpha _2}{M_{\rm{2}}}}}} \right)^{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}}\left[ {1 - f\left( {{{{\tau _2}} \mathord{\left/ {\vphantom {{{\tau _2}} {{t_{\rm{U}}}}}} \right. \kern-\nulldelimiterspace} {{t_{\rm{U}}}}}} \right)} \right]\quad ,$$
$${h_{\rm{U}}} = {\left( {{{{P_{\rm{U}}}} \mathord{\left/ {\vphantom {{{P_{\rm{U}}}} {{\alpha _1}H}}} \right. \kern-\nulldelimiterspace} {{\alpha _1}H}}} \right)^{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}} + {\left( {{{{P_{\rm{U}}}} \mathord{\left/ {\vphantom {{{P_{\rm{U}}}} {{\alpha _2}{M_{\rm{1}}}}}} \right. \kern-\nulldelimiterspace} {{\alpha _2}{M_{\rm{1}}}}}} \right)^{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}}\left[ {1 - f\left( {{{{\tau _1}} \mathord{\left/ {\vphantom {{{\tau _1}} {{t_{\rm{U}}}}}} \right. \kern-\nulldelimiterspace} {{t_{\rm{U}}}}}} \right)} \right] + {\left( {{{{P_{\rm{U}}}} \mathord{\left/ {\vphantom {{{P_{\rm{U}}}} {{\alpha _2}{M_{\rm{2}}}}}} \right. \kern-\nulldelimiterspace} {{\alpha _2}{M_{\rm{2}}}}}} \right)^{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}}\left[ {1 - f\left( {{{{\tau _2}} \mathord{\left/ {\vphantom {{{\tau _2}} {{t_{\rm{U}}}}}} \right. \kern-\nulldelimiterspace} {{t_{\rm{U}}}}}} \right)} \right]\quad ,$$
where the functions f are defined by Eq. (9) or (10) and depend only on the ratio of a material time constant and the experimental rise time. If the latter is fixed the values of the functions are fixed and hence the ratio of the first and second terms (the ratio of plastic and viscoelastic deformation) is also fixed. Equation (10a) also makes clear that load and loading rate also do not affect this ratio (providing material properties do not change with load). As the rise time used in Fig. 4 was fixed and long enough to capture the fast and slow viscoelastic processes, the relative contributions to total displacement and thus the shape of the load–displacement curves remained invariant; consistent with Eq. (10a), the predictions scaled simply with peak load over the load range used. (It is possible that plastic deformation will not be initiated or will be suppressed at very small loads, in which case H would be load-dependent; this was not observed here.)
Figure 5 shows as symbols the load–displacement behavior of all the monolithic materials during linear load ramps with a rise time of 1000 s. The solid lines in Fig. 5 are predictions of the load–displacement responses using Eq. (10) and the fitted mechanical deformation parameters, α1 H, α2 M 1, α2 M 2, τ1, and τ2 for each material. In all cases, the predictions are very good fits to the measurements. It is clear that SLG is much more resistant and HDPE much less resistant to indentation deformation under these conditions than the rest of the materials. It is also clear from the fits in Fig. 5 that the form of the analysis applies to a range of materials that exhibit viscoelastic and plastic deformation during pyramidal indentation. Comparison of the magnitudes of the fitted parameters α1 H and α2 M 1 with commonly used values of hardness and Young's modulus Reference Callister39,40 for each material suggests that a very good approximation is that α1 and α2 are constants, and that the group of materials is well described by α1 = 100 and α2 = 6. Using these α parameters, Table I gives the values of τ1, M 1, τ2, M 2, and H determined for each material, where the values represent the experimental means and standard deviations of best–fit parameters from four separate experiments. The H values are comparable to those determined using quasi-static indentation 40 and prior VEP methods. Reference Oyen and Cook1,Reference Oyen, Cook, Emerson and Moody2,Reference Cook and Oyen4,Reference Olesiak, Oyen and Ferguson7,Reference Mazeran, Beyaoui, Bigerelle and Guigon9,Reference Oyen20 The time constants are also comparable to those observed in indentation measurements in which a two time-constant model was used: a few tens of seconds for τ1 and a few hundreds of seconds for τ2. Reference Zhang, Zhang, Zeng and Shen3,Reference Mazeran, Beyaoui, Bigerelle and Guigon9,Reference Oyen18 The viscoelastic resistance parameters are comparable to those that can be inferred from a similar study, Reference Mazeran, Beyaoui, Bigerelle and Guigon9 a few gigapascals for M 1 and a few tens of gigapascals for M 2, but the comparison is not direct as the prior study used a slightly different indentation model. A final point of comparison is that for SLG, which exhibited much greater resistance to viscoelastic deformation than the polymeric materials but similar time constants, in particular for the fast deformation process characterized by τ1 = 11 s. Such time dependence is consistent with earlier observations of hysteretic cyclic indentation of SLG at similar indentation time scales. Reference Oliver and Pharr41,Reference Thurn and Cook42
TABLE I. Viscoelastic and plastic properties of materials.

B. Viscoelastic and plastic property mapping
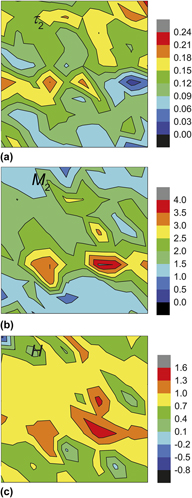
Figure 6 shows property maps as color-fill contours over the same area for an extreme example of a change in properties at the Epoxy2-AlN interface; the interface is vertical and is located 400 µm from the left edge of the images. To accommodate the extreme range of properties, Figs. 6(a)–6(c) use logarithmic contour intervals. Figure 6(a) is a map of the viscoelastic resistance parameter M 1. At this scale the epoxy appears uniform and is weakly resistant to viscoelastic deformation. The AlN ceramic is significantly more resistant to viscoelastic deformation and exhibits some variability in resistance (the weakening adjacent to the interface reflects the large contour intervals). Figure 6(b) is a similar map of the plastic resistance H; the appearance is similar to Fig. 6(a). In this extreme example of material changes, the interface between the epoxy and the ceramic appears sharp in both viscoelastic and plastic properties maps. Figure 6(c) is a map of the viscoelastic time constant τ1; although the interface is less distinct, there is still a significant difference between the epoxy and the AlN, and there appears to be a correlation between M 1 and τ1 in the ceramic (in some regions there is more resistance to viscoelastic deformation and it is slower). Variability in the properties of the epoxy can be observed by changing the contour scale and this is shown in Fig. 6(d), which is a re-scaled map of H for the epoxy alone. The epoxy plastic resistance varies by approximately ±15% relatively but there does not seem to be an interface proximity effect as observed in the ceramic, Fig. 6(b).

FIG. 6. Color-fill contour maps of mechanical properties variations at an epoxy-AlN interface; the epoxy extends 400 µm from the left of the maps as indicated by the arrow. (a) The resistance to viscoelastic deformation, M 1, for the fast process in the epoxy. (b) The resistance to plastic deformation, H. (c) The viscoelastic deformation time constant, τ1, for the fast process. (d) The resistance to plastic deformation, H, in the epoxy, re-scaled to enhance variation.
Figures 7 and 8 show the variations in properties along line scans for the 1% and 5% CNT-epoxy composites, respectively. The gray bands represent the mean ± two standard deviation limits (given in Table I) of the properties determined for Epoxy1, the composite matrix. The symbols represent individual measurements in each of three separate scans; different symbols are used for each scan and the lines are guides to the eye. The composite materials exhibited both similarities and differences in comparison with the matrix material. For both composites, the time constants and resistances for the fast viscoelastic process, τ1 and M 1, top diagrams, were not significantly different from those of the matrix. For both composites, the time constants and resistances for the slow viscoelastic process, τ2 and M 2, center diagrams, were significantly greater than those of the matrix, particularly so for the slow viscoelastic resistance, M 2. Similarly, for both composites, the resistances to plastic deformation, H, bottom diagrams, were significantly greater than that of the matrix. A significant difference between the composites was the variability in properties along the line scan. The 5% composite exhibited much greater variability in all properties than the 1% composite, particularly so for M 2 and H.

FIG. 7. Variations in mechanical properties of 1% CNT-epoxy composite along line scans. The gray bands indicate the properties of the epoxy matrix. (Upper) Time constant and resistance to deformation for the fast viscoelastic deformation process, (τ1, M 1). (Central) Time constant and resistance to deformation for the slow viscoelastic deformation process, (τ2, M 2). (Lower) Resistance to plastic deformation, H.

FIG. 8. Variations in mechanical properties of 5% CNT-epoxy composite along line scans. Notation as in Fig. 7.
Figures 9 and 10 show property maps for the 1% and 5% CNT-epoxy composites, respectively. These maps provide pictorial illustrations of the above similarities and differences, as well as allowing an assessment of the composite microstructures and the characteristic length scales for variability or heterogeneity. For ease of comparison, the maps are given as color-filled contours of relative properties, X*:
such that X* = 0 corresponds to no difference from the matrix; the properties considered were X = τ2, M
2, and H and the same contour intervals were used for each material. Figures 9(a) and 10(a) show maps of the relative time constants
![]() $\tau _2^ *$
for the 1% and 5% composites, respectively. In both cases, the “slow” process in the composite is even slower than that in the matrix (
$\tau _2^ *$
for the 1% and 5% composites, respectively. In both cases, the “slow” process in the composite is even slower than that in the matrix (
![]() $\tau _2^ * > 0$
) and the variability and average of the time constant is greater in the 5% material. Figures 9(b) and 10(b) show maps of the relative viscoelastic resistance
$\tau _2^ * > 0$
) and the variability and average of the time constant is greater in the 5% material. Figures 9(b) and 10(b) show maps of the relative viscoelastic resistance
![]() $M_2^ *$
for the 1% and 5% composites. In both cases, resistance to the slow deformation process is greater than that in the matrix, particularly so for the 5% material. Finally, Figs. 9(c) and 10(c) show maps of the relative plastic resistance H* for the 1% and 5% composites. In this case, although the resistance to plastic deformation is mostly greater than that of the matrix, there are local “soft” spots (H* < 0). The maps of Figs. 9 and 10 are of course consistent with the graphs of Figs. 7 and 8 with regard to values and variability, but they provide two additional features. The first is that the form and length scales of the microstructures can easily be observed. The maps suggest that the microstructures are “clumped” with localized regions that are more resistant to deformation, and that these regions are approximately 200 µm in size in 1% material and about 500 µm in size in 5% material. The second is that correlations between properties can easily be observed. The maps suggest that there is a strong correlation between the resistances to viscoelastic and plastic deformation [maps (b) and (c)] and a weaker correlation between the viscoelastic time constant and resistance [maps (a) and (b)].
$M_2^ *$
for the 1% and 5% composites. In both cases, resistance to the slow deformation process is greater than that in the matrix, particularly so for the 5% material. Finally, Figs. 9(c) and 10(c) show maps of the relative plastic resistance H* for the 1% and 5% composites. In this case, although the resistance to plastic deformation is mostly greater than that of the matrix, there are local “soft” spots (H* < 0). The maps of Figs. 9 and 10 are of course consistent with the graphs of Figs. 7 and 8 with regard to values and variability, but they provide two additional features. The first is that the form and length scales of the microstructures can easily be observed. The maps suggest that the microstructures are “clumped” with localized regions that are more resistant to deformation, and that these regions are approximately 200 µm in size in 1% material and about 500 µm in size in 5% material. The second is that correlations between properties can easily be observed. The maps suggest that there is a strong correlation between the resistances to viscoelastic and plastic deformation [maps (b) and (c)] and a weaker correlation between the viscoelastic time constant and resistance [maps (a) and (b)].

FIG. 9. Color-fill contour maps of mechanical properties variations in 1% CNT-epoxy composite. The properties are plotted relative to the epoxy matrix using Eq. (11). (a) The viscoelastic time constant, τ2, for the slow deformation process. (b) The resistance to viscoelastic deformation, M 2, for the slow process. (c) The resistance to plastic deformation, H.

FIG. 10. Color-fill contour maps of mechanical properties variations in 5% CNT-epoxy composite. Notation as in Fig. 9.
IV. DISCUSSION AND CONCLUSIONS
The results presented here have demonstrated two-dimensional mapping of viscoelastic and plastic properties of polymeric-based materials, extending the mapping capabilities to time-dependent deformation from those demonstrated previously Reference Engqvist and Wiklund32–Reference Goldbaum, Chromik, Brodusch and Gauvin37 using an elastic–plastic analysis. Reference Oliver and Pharr41 The previous studies all used indentation spacings smaller than the 100 µm used here, ranging from 0.5 µm Reference Engqvist and Wiklund32 –20 µm, Reference Zhu, Hughes, Bicanic and Pearce35 allowing most maps to be presented with properties as individual pixels Reference Engqvist and Wiklund32,Reference Gupta, Stachewicz, Wagermaier, Roschger, Wagner and Fratzl34–Reference Randall, Vandamme and Ulm36 rather than as contours Reference Cuy, Mann, Livi, Teaford and Weihs33,Reference Goldbaum, Chromik, Brodusch and Gauvin37 as in Figs. 6, 9 and 10. In both the viscoelastic-plastic mapping here and in the previous elastic–plastic maps, the indentation spacing was matched to the scale of the microstructure and as a consequence there are many similarities between the previous maps and those obtained here: In previous maps of dense WC polycrystals, Reference Engqvist and Wiklund32 tooth enamel, Reference Cuy, Mann, Livi, Teaford and Weihs33 lamellar bone, Reference Gupta, Stachewicz, Wagermaier, Roschger, Wagner and Fratzl34 quartzite, Reference Zhu, Hughes, Bicanic and Pearce35 brass, Reference Randall, Vandamme and Ulm36 and titanium, Reference Goldbaum, Chromik, Brodusch and Gauvin37 there were factors of two or three variation in modulus and hardness observed over the maps. These variations were associated with microstructural variations such as grain orientation or small variations in composition and are analogous to the variations in properties observed within the AlN ceramic and epoxy, Fig. 6. In some cases, much greater variations in properties were observed and were associated with abrupt changes in microstructure, such as decreases of factors of four in modulus and hardness associated with Co binder in WC–Co composites, Reference Engqvist and Wiklund32 decreases of factors of ten associated with graphite flakes in cast iron, Reference Randall, Vandamme and Ulm36 and much greater decreases associated with porosity in bone Reference Gupta, Stachewicz, Wagermaier, Roschger, Wagner and Fratzl34 and cement. Reference Zhu, Hughes, Bicanic and Pearce35 These latter variations are analogous to the variations in properties observed between the AlN and epoxy, Fig. 6.
The above observations and those of prior CNT-epoxy dispersion studies Reference Sandler, Shaffer, Prasse, Bauhofer, Schulte and Windle28,Reference Chakraborty, Plyhm, Barbezat, Necola and Terrasi31 and reviews Reference Xie, Mai and Zhou29,Reference Ma, Siddiqui, Marom and Kim30 enable interpretation of the line scans and maps of Figs. 7–10 in terms of the CNT composite microstructures. Figures 7 and 8 show that in both composites the time constant and deformation resistance of the fast viscoelastic process (τ1, M 1) are no different from that of the epoxy matrix. This observation suggests that the CNTs do not influence this deformation mechanism at all and that it is entirely associated with the epoxy and probably molecular in scale. Conversely, Figs. 7 and 8 show that for the slow viscoelastic process (τ2, M 2) in both composites the time constant is increased somewhat and the deformation resistance is increased substantially from that of the epoxy. The implication here is that the incorporated CNTs are slowing this deformation process and making it more difficult, probably over length scales comparable to the indentation size, about 5 µm (Fig. 5). Figures 7 and 8 also show that the resistance to plastic deformation, H, is increased substantially from that of the epoxy for both composites, consistent with the idea that the CNTs impeded both slow, time-dependent and irreversible, time-independent-deformation on length scales comparable to the indentation field. Figures 9 and 10 highlight, however, that the increases in M 2 and H are not uniform: some areas exhibit less than average deformation resistance, e.g., in Fig. 9, and some areas exhibit greater than average deformation resistance, e.g., in Fig. 10, with strong correlation between M 2 and H. These areas probably reflect localized increased concentrations of CNTs and are comparable in size to the hundreds of micrometer- Reference Chakraborty, Plyhm, Barbezat, Necola and Terrasi31 to millimeter-scale Reference Sandler, Shaffer, Prasse, Bauhofer, Schulte and Windle28 agglomerates observed previously. Removal of such entangled agglomerates is a major focus of the many methods Reference Xie, Mai and Zhou29,Reference Ma, Siddiqui, Marom and Kim30 used to disperse CNTs in polymer matrices, as the agglomerates are only weakly infiltrated by the polymer and thereby degrade the composite properties relative to those that might be achieved by well-dispersed CNTs bound to the matrix. This degradation is probably the case in Fig. 9, which shows local “soft” spots. Counter to this is Fig. 10, which shows local “hard” spots possibly reflecting enhanced areas of CNT concentration with adequate polymer infiltration. The advantage of maps such as Figs. 9 and 10 is that local variations in properties are assessed directly and do not have to be inferred from measurements of entire composite components. Reference Chakraborty, Plyhm, Barbezat, Necola and Terrasi31 An implication from Figs. 7–10 is that the CNTs in the 5% material were less uniformly dispersed than in the 1% material. Imaging spectroscopy methods, e.g., Raman spectroscopy as applied to single-wall CNT composites, Reference Du, Scogna, Zhou, Brand, Fischer and Winey43 could possibly be used to directly assess CNT dispersion for comparison with the mechanical measurements.
Application of the method developed here to prediction of properties for a particular material requires a few additional steps. First, to establish accuracy (how close a measurement represents a true or known value), independent measurements of properties should be performed so as to fix the geometry terms α1 and α2 for the materials class under consideration. The material-invariant approximation used here returns reasonable property values (Sec. III.A and Table I) for a range of materials, but does not necessarily apply in detail to a specific material. Such independent measurements should be viscoelastic experiments, noting that the M values used here are viscoelastic resistances and include elastic moduli as lower bounds. Second, to establish precision (how close a measurement represents a mean value) sufficient measurements should be performed to place statistical bounds on the determined τ1, M 1, τ2, M 2, and H parameters. Table I suggests that four measurements provide sufficient precision for homogeneous materials at the indentation scale used here, but indentations at smaller scales, particularly in materials with heterogeneous microstructures, will lead to less precision (e.g., as in the elastic–plastic indentation studies above Reference Engqvist and Wiklund32,Reference Randall, Vandamme and Ulm36,Reference Goldbaum, Chromik, Brodusch and Gauvin37 ) and require greater numbers of indentations. This last point pertains particularly to composite materials: If globally averaged properties are required for a composite, say to predict the overall response of a component, sufficient numbers of indentations over a large enough area are required so as to assess the characteristic length scales of the microstructure. This in turn sets the “representative volume element” for the material that is the minimum component scale that can be regarded as possessing average properties. Third, to validate the assumed constitutive law and measured deformation parameters, predictions should be made and tested against loading protocols close to those expected in component operation, or at least different from those used to determine the parameters. Here, predictions from the three-segment measurements (Fig. 2) were tested against ramp loading protocols (Figs. 3–5) for which closed-form solutions [Eq. (10)] were developed. Similar validations are often performed, Reference Oyen and Cook1,Reference Oyen, Cook, Emerson and Moody2,Reference Cook and Oyen4,Reference Wang and Lloyd8,Reference Oyen18–Reference Oyen20 but often not, especially when viscoelastic correspondence methods are used to analyze measurements. Reference Zhang, Zhang, Zeng and Shen3,Reference Mazeran, Beyaoui, Bigerelle and Guigon9,Reference Isaza, Mazeran, El Kirat and Ho Ba Tho12,Reference Cheng, Xia, Yu, Scriven and Gerberich13,Reference Yang, Zhang and Zeng16,Reference Cheng, Xia, Scriven and Gerberich17 In this regard, it is to be noted that for nonsimple loading protocols or those with multiple stages, the integrand of the general displacement integral [Eq. (A5)] will usually not be too pathological and therefore amenable to straightforward numerical integration. It is also to be noted that the viscoelastic correspondence methods Reference Lee and Radok23–Reference Ting27 do not allow for unloading of the indenter (formally, they only allow monotonically increasing contact radius), which is not an inherent limitation of the VEP approach and which can be tested experimentally. Reference Cook and Oyen4,Reference Mazeran, Beyaoui, Bigerelle and Guigon9,Reference Isaza, Mazeran, El Kirat and Ho Ba Tho12 Extension to arbitrary, multiple-stage loading protocols including unloading and numerical prediction of load–displacement–time responses will be the subject of future work.
Finally, practical considerations for indentation-based mapping of the mechanical properties of polymeric systems are that time will nearly always be an inherent part of the measurement procedure and that the indentations will invariably be large. Hence, maps that involve viscoelastic properties will always take longer to generate than those that only involve elastic–plastic properties, and maps of “soft” materials will always require indentation spacing greater than that of hard materials. As noted above, matching the indentation spacing and size to the length scale of the microstructure is important such that maps do not over- or under-sample. In polymeric composite systems with microstructural scales smaller than that examined here, finely spaced line scans about three indentation dimensions apart might provide a compromise between generating an accurate assessment of the heterogeneity of time-dependent mechanical responses and maintaining reasonable test durations.
ACKNOWLEDGMENTS
This research was performed while AJG was initially an undergraduate student volunteer researcher at NIST and subsequently a member of the NIST Summer Undergraduate Research Fellowship (SURF) program. The authors thank APV Engineered Coatings and Arkema for assistance with sample preparation and Drs. Doug Smith and Brian Bush of NIST for experimental assistance. Certain commercial equipment, instruments or materials are identified in this document. Such identification does not imply recommendation or endorsement by the National Institute of Standards and Technology, nor does it imply that the products identified are necessarily the best available for the purpose.
APPENDIX: VEP MODEL DEVELOPMENT
The starting point for the quadratic viscoelastic Kelvin element is the linear Kelvin element load–displacement function: Reference Findley, Lai and Onaran38
where k is interpreted as a stiffness, η is interpreted as a viscosity, and the load is interpreted as the sum of the loads supported by an elastic element (k) and a viscous element (η) in parallel. Equation (A1) can be re-written as
where
is a characteristic time constant. By analogy with the quadratic viscous element described by Eq. (3), the quadratic viscoelastic Kelvin element is described by squaring the right side of Eq. (A2a),
where the term α2 Mτ Reference Oyen, Cook, Emerson and Moody2 is here an effective or lumped quadratic viscoelastic resistance. The first term in the parentheses in Eq. (A3) represents the elastic contribution to the resistance and the second term the viscous contribution. Inverting Eq. (A3) leads to a differential equation for the viscoelastic displacement resulting from an imposed load spectrum:
This is a differential equation of the form
with R and Q defined by Eq. (A4) that can be solved with use of an integrating factor
with solution
where C is a constant of integration. Hence, the viscoelastic displacement can be written as
The time spectra of interest here are linear, of the form
In particular, for a ramp load from zero to a peak of P R in a time of t R, A = 0 and B = P R/t R in Eq. (A6), and the solution to Eq. (A5) is, using Mathematica, 44
where
The function erfi(z) is the complex error function given by erfi(z) = −ierf(z), where erf(z) is the general error function, z is complex, and i Reference Oyen, Cook, Emerson and Moody2 = −1. It is easy to show that if the argument z = x is real that erfi(x) = erf(x). This is case here, Eq. (A7a), such that
using h = 0 at t = 0 to show that C = 0, and where the notation for erf(x)1/2 in Eq. (A8) follows directly from Eq. (A7a). The first term on the right side of Eq. (A8) represents the displacement of a free elastic element and the second term represents the modification by the viscous element. Setting t = t R in Eq. (A8) gives h(t R) = h R, the viscoelastic displacement at the peak of the ramp load.
For a load hold at the peak value, after a ramp, A = P R and B = 0 in Eq. (A6), and the solution to Eq. (A5) is, using separation of variables,
where
The term h
R appears in both additive and multiplicative roles on the right side of Eq. (A9a), modifying the creep response [Eq. (A9)] by displacement accrued during the prior ramp [Eq. (A8)]. In this sense, h
R acts as a “ramp correction factor” used earlier in a linear viscoelastic context.
Reference Oyen18,Reference Mattice, Lau, Oyen and Kent19
Eq. (A9) contains an essential result of the analysis: For (t − t
R) >> τ the creep displacement approaches a bounded value of
![]() $h \to {\left( {{{{P_R}} \mathord{\left/ {\vphantom {{{P_R}} {{\alpha _2}M}}} \right. \kern-\nulldelimiterspace} {{\alpha _2}M}}} \right)^{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}}$
in a nonlinear manner.
$h \to {\left( {{{{P_R}} \mathord{\left/ {\vphantom {{{P_R}} {{\alpha _2}M}}} \right. \kern-\nulldelimiterspace} {{\alpha _2}M}}} \right)^{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}}$
in a nonlinear manner.
Alternatively, for a ramp unload from the peak of P R to zero in a time of t R, A = 2 P R and B = −P R/t R in Eq. (A6), and the solution to Eq. (A5) is, using Mathematica, 44
 $$h = {\left( {a + bt} \right)^{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}} - {{\sqrt \pi } \over 2}{\left( {b\tau } \right)^{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}}\exp \left( {{{a + bt} \over {b\tau }}} \right){\rm{erf}}{\left( {{{a + bt} \over {b\tau }}} \right)^{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}} + {h_{\rm{F}}}\exp \left( {{{a + bt} \over {b\tau }}} \right),\;{t_{\rm{R}}} \,\,\le\,\, t \,\,\le\,\, 2{t_{\rm{R}}}\quad ,$$
$$h = {\left( {a + bt} \right)^{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}} - {{\sqrt \pi } \over 2}{\left( {b\tau } \right)^{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}}\exp \left( {{{a + bt} \over {b\tau }}} \right){\rm{erf}}{\left( {{{a + bt} \over {b\tau }}} \right)^{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}} + {h_{\rm{F}}}\exp \left( {{{a + bt} \over {b\tau }}} \right),\;{t_{\rm{R}}} \,\,\le\,\, t \,\,\le\,\, 2{t_{\rm{R}}}\quad ,$$
where now
Setting t = 2t R in Eqs. (A10a) and (A10b) gives h(2t R) = h F, the displacement at the end of the triangular load spectrum. Noting that both Eqs. (A8), (A10a) and (A10b) must pertain at t = t R, h F can be determined in terms of h R and thus in terms of test and material parameters.
Combining Eqs. (A8), (A10a) and (A10b) generates load–displacement responses that are indistinguishable from those observed in experiments and determined using the earlier Maxwell-like VEP model during triangle-wave loading. Reference Oyen and Cook1,Reference Cook and Oyen4 In particular, for slow tests the current model exhibits the initial negative unloading slope and unloading “nose.” The explicit behavior described by Eqs. (A10a) and (A10b) will not be used here, but it is noted that in a zero-load recovery segment after a triangular load spectrum, such that A = B = 0, the viscoelastic displacement is given by the last term in Eq. (A5) alone, such that
Equation (A11) contains another essential result of the analysis: For (t − 2t R) >> τ in a recovery segment, the viscoelastic displacement h → 0 in a nonlinear manner.