Article contents
Characterization of power-law creep in the solid-acid CsHSO4 via nanoindentation
Published online by Cambridge University Press: 06 February 2019
Abstract
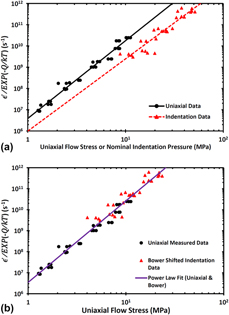
A high-temperature nanoindentation system was used to examine the steady state indentation creep behavior of CsHSO4. This high proton conductivity solid-acid material is a candidate for use as a solid-state electrolyte in intermediate temperature fuel cells. Constant strain rate indentation creep tests yielded a stress exponent and a creep activation energy in close agreement with results obtained from previous uniaxial compression testing. The large penetration depths reached during creep testing necessitated validating an indenter area function well beyond depths measurable in fused silica. The developed methodology is material agnostic meaning it can be used for indentation creep measurements in other high creep rate materials. In addition, it is shown how an analysis developed by Bower et al. (Proc. Royal Soc. 441, 97–124, 1993) can be successfully used to convert the indentation creep parameters into the more common material parameters measured in uniaxial creep tests.
- Type
- Article
- Information
- Journal of Materials Research , Volume 34 , Issue 7: Focus Section: Interconnects and Interfaces in Energy Conversion Materials , 15 April 2019 , pp. 1130 - 1137
- Copyright
- Copyright © Materials Research Society 2019
Footnotes
This author was an editor of this journal during the review and decision stage. For the JMR policy on review and publication of manuscripts authored by editors, please refer to http://www.mrs.org/jmr-editor-manuscripts/.
References
- 7
- Cited by


