Research Article
Quillen model categories
-
- Published online by Cambridge University Press:
- 04 March 2013, pp. 469-478
-
- Article
- Export citation
Injective stability for unitary K1, revisited
-
- Published online by Cambridge University Press:
- 06 March 2013, pp. 233-242
-
- Article
- Export citation
Cycles de codimension 2 et H3 non ramifié pour les variétés sur les corps finis
-
- Published online by Cambridge University Press:
- 04 February 2013, pp. 1-53
-
- Article
- Export citation
Beilinson's Hodge Conjecture for Smooth Varieties
-
- Published online by Cambridge University Press:
- 06 March 2013, pp. 243-282
-
- Article
- Export citation
On the Functoriality of the Slice Filtration
-
- Published online by Cambridge University Press:
- 11 February 2013, pp. 55-71
-
- Article
- Export citation
Editorial
The Legacy of Daniel Quillen
-
- Published online by Cambridge University Press:
- 10 October 2013, pp. 465-467
-
- Article
-
- You have access
- Export citation
Research Article
Algebraic cobordism theory attached to algebraic equivalence
-
- Published online by Cambridge University Press:
- 06 March 2013, pp. 73-112
-
- Article
- Export citation
Daniel Quillen, the father of abstract homotopy theory
-
- Published online by Cambridge University Press:
- 01 March 2013, pp. 479-491
-
- Article
- Export citation
Godeaux–Serre varieties and the étale index
-
- Published online by Cambridge University Press:
- 04 April 2013, pp. 283-295
-
- Article
- Export citation
Central simple algebras of prime exponent and divided power operations
-
- Published online by Cambridge University Press:
- 15 January 2013, pp. 113-123
-
- Article
- Export citation
Quillen's work on formal group laws and complex cobordism theory
-
- Published online by Cambridge University Press:
- 01 March 2013, pp. 493-506
-
- Article
- Export citation
Module categories for group algebras over commutative rings
-
- Published online by Cambridge University Press:
- 06 March 2013, pp. 297-329
-
- Article
- Export citation
Prime Ideals of Mixed Artin-Tate Motives
-
- Published online by Cambridge University Press:
- 06 March 2013, pp. 331-349
-
- Article
- Export citation
Spectrum of group cohomology and support varieties
-
- Published online by Cambridge University Press:
- 01 March 2013, pp. 507-516
-
- Article
- Export citation
On a Localisation Sequence for the K-Theory of Skew Power Series Rings
-
- Published online by Cambridge University Press:
- 21 February 2013, pp. 125-154
-
- Article
- Export citation
K1 of Exact Categories by Mirror Image Sequences
-
- Published online by Cambridge University Press:
- 19 April 2012, pp. 155-181
-
- Article
- Export citation
Algebraic cycles satisfying the Maurer-Cartan equation and the unipotent fundamental group of curves
-
- Published online by Cambridge University Press:
- 04 April 2013, pp. 351-392
-
- Article
- Export citation
Quillen's work on the Adams Conjecture
-
- Published online by Cambridge University Press:
- 11 March 2013, pp. 517-526
-
- Article
- Export citation
Quillen's work in algebraic K-theory
-
- Published online by Cambridge University Press:
- 11 March 2013, pp. 527-547
-
- Article
- Export citation
Extensions panachées autoduales
-
- Published online by Cambridge University Press:
- 06 March 2013, pp. 393-411
-
- Article
- Export citation

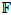 . We discuss the unramified cohomology group
. We discuss the unramified cohomology group 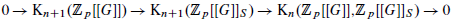
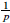 ] with respect to the Ore set
] with respect to the Ore set 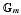 , we construct such a sequence of algebraic cycles whose image under the cycle map gives rise to the étale unipotent fundamental group of the curve.
, we construct such a sequence of algebraic cycles whose image under the cycle map gives rise to the étale unipotent fundamental group of the curve.