Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-21T15:39:06.106Z Has data issue: false hasContentIssue false
  • English
  • Français

Bimonads and Hopf monads on categories

Published online by Cambridge University Press:  05 February 2010

Bachuki Mesablishvili  and
Robert Wisbauer
Bachuki Mesablishvili
Affiliation:
Razmadze Mathematical Institute, Tbilisi 0193, Republic of Georgia, bachi@rmi.acnet.ge
Robert Wisbauer
Affiliation:
Department of Mathematics of HHU, 40225 Düsseldorf, Germany, wisbauer@math.uni-duesseldorf.de
Get access

Abstract

The purpose of this paper is to develop a theory of bimonads and Hopf monads on arbitrary categories thus providing the possibility to transfer the essentials of the theory of Hopf algebras in vector spaces to more general settings. There are several extensions of this theory to monoidal categories which in a certain sense follow the classical trace. Here we do not pose any conditions on our base category but we do refer to the monoidal structure of the category of endofunctors on any category 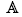and by this we retain some of the combinatorial complexity which makes the theory so interesting. As a basic tool we use distributive laws between monads and comonads (entwinings) on 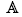: we define a bimonad on 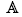as an endofunctor B which is a monad and a comonad with an entwining λ : BB → BB satisfying certain conditions. This λ is also employed to define the category 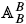of (mixed) B-bimodules. In the classical situation, an entwining λ is derived from the twist map for vector spaces. Here this need not be the case but there may exist special distributive laws τ : BB → BB satisfying the Yang-Baxter equation (local prebraidings) which induce an entwining λ and lead to an extension of the theory of braided Hopf algebras.

An antipode is defined as a natural transformation S : B → B with special properties. For categories 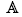with limits or colimits and bimonads B preserving them, the existence of an antipode is equivalent to B inducing an equivalence between 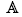and the category 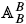of B-bimodules. This is a general form of the Fundamental Theorem of Hopf algebras.

Finally we observe a nice symmetry: If B is an endofunctor with a right adjoint R, then B is a (Hopf) bimonad if and only if R is a (Hopf) bimonad. Thus a k-vector space H is a Hopf algebra if and only if Homk(H,−) is a Hopf bimonad. This provides a rich source for Hopf monads not defined by tensor products and generalises the well-known fact that a finite dimensional k-vector space H is a Hopf algebra if and only if its dual H* = Homk(H,k) is a Hopf algebra. Moreover, we obtain that any set G is a group if and only if the functor Map(G,−) is a Hopf monad on the category of sets.

Keywords

BialgebrasbimomadsHopf algebrasHopf monadsdistributive laws
Type
Research Article
Information
Journal of K-Theory , Volume 7 , Issue 2 , April 2011 , pp. 349 - 388
Copyright
Copyright © ISOPP 2010

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Barr, M., Composite cotriples and derived functors, in: Sem. Triples Categor. Homology Theory, Springer LN Math. 80, 336–356 (1969)CrossRefGoogle Scholar
2.Beck, J., Distributive laws, in: Seminar on Triples and Categorical Homology Theory, Eckmann, B. (ed.), Springer LNM 80, 119–140 (1969)CrossRefGoogle Scholar
3.Bespalov, Y. and Drabant, B., Hopf (bi-)modules and crossed modules in braided monoidal categories, J. Pure Appl. Algebra 123(1-3), 105–129 (1998)CrossRefGoogle Scholar
4.Bespalov, Y., Kerler, Th., Lyubashenko, V. and Turaev, V., Integrals for braided Hopf algebras, J. Pure Appl. Algebra 148(2), 113–164 (2000)CrossRefGoogle Scholar
5.Böhm, G., Brzeziński, T. and Wisbauer, R., Monads and comonads in module categories, J. Algebra 322, 1719–1747 (2009)CrossRefGoogle Scholar
6.Borceux, F. and Dejean, D., Cauchy completion in category theory, Cah. Topol. Géom. Différ. Catégoriques 27, 133–146 (1986)Google Scholar
7.Bruguières, A. and Virelizier, A., Hopf monads, Adv. Math. 215(2), 679–733 (2007)CrossRefGoogle Scholar
8.Brzeziński, T. and Wisbauer, R., Corings and Comodules, London Math. Soc. Lecture Note Series 309, Cambridge University Press (2003)Google Scholar
9.Day, B., McCrudden, P. and Street, R., Dualizations and antipodes, Appl. Categ. Struct. 11(3), 229–260 (2003)CrossRefGoogle Scholar
10.Dubuc, E., Kan extensions in enriched category theory, Lecture Notes in Mathematics 145, Berlin-Heidelberg-New York: Springer-Verlag (1970)Google Scholar
11.Eilenberg, S. and Moore, J.C., Adjoint functors and triples, Ill. J. Math. 9, 381–398 (1965)Google Scholar
12.Gumm, H.P., Universelle Coalgebra, in: Allgemeine Algebra, Ihringer, Th., Berliner Stud. zur Math., Band 10, 155–207, Heldermann Verlag (2003)Google Scholar
13.Kelly, G.M. and Street, R., Review of the elements of 2-categories, Category Sem., Proc., Sydney 1972/1973, Lect. Notes Math. 420, 75–103 (1974)CrossRefGoogle Scholar
14.Lack, S. and Street, R., The formal theory of monads II, J. Pure Appl. Algebra 175(1-3), 243–265 (2002)CrossRefGoogle Scholar
15.Loday, J.-L., Generalized bialgebras and triples of operads, Astérisque 320 (2008), arXiv:math/0611885Google Scholar
16.López Franco, I., Formal Hopf algebra theory I : Hopf modules for pseudomonoids, J. Pure Appl. Algebra 213, 1046–1063 (2009)CrossRefGoogle Scholar
17.McCrudden, P., Opmonoidal monads, Theory Appl. Categ. 10, 469–485 (2002)Google Scholar
18.Mesablishvili, B., Descent in categories of (co)algebras, Homology, Homotopy and Applications 7, 1–8 (2005)CrossRefGoogle Scholar
19.Mesablishvili, B., Monads of effective descent type and comonadicity, Theory Appl. Categ. 16, 1–45 (2006)Google Scholar
20.Mesablishvili, B., Entwining Structures in Monoidal Categories, J. Algebra 319(6), 2496–2517 (2008)CrossRefGoogle Scholar
21.Moerdijk, I., Monads on tensor categories, J. Pure Appl. Algebra 168(2-3), 189–208 (2002CrossRefGoogle Scholar
22.Power, J. and Watanabe, H., Combining a monad and a comonad, Theor. Comput. Sci. 280(1-2), 137–162 (2002)CrossRefGoogle Scholar
23.Schubert, H., Categories, Berlin-Heidelberg-New York, Springer-Verlag (1972)CrossRefGoogle Scholar
24.Street, R., Frobenius monads and pseudomonoids, J. Math. Phys. 45(10), 3930–3948 (2004)CrossRefGoogle Scholar
25.Szlachányi, K., Adjointable monoidal functors and quantum groupoids, Caenepeel, S. (ed.) et al., Hopf algebras in noncommutative geometry and physics, Proc. conf. on Hopf algebras and quantum groups, Brussels 2002, Marcel Dekker LN PAM 239, 291–307 (2005)Google Scholar
26.Takeuchi, M., Survey of braided Hopf algebras, in: New trends in Hopf algebra theory, Proc. Coll. Quantum Groups and Hopf Algebras, La Falda, Argentina 1999, Andruskiewitsch, N. et al. (ed.), Providence, RI: American Math. Soc., Contemp. Math. 267, 301–323 (2000)CrossRefGoogle Scholar
27.Turi, D. and Plotkin, G., Towards a mathematical operational semantics, Proceedings 12th Ann. IEEE Symp. on Logic in Computer Science, LICS'97, Warsaw, Poland (1997)Google Scholar
28.Wisbauer, R., On Galois comodules, Commun. Algebra 34(7), 2683–2711 (2006)CrossRefGoogle Scholar
29.Wisbauer, R., Algebras versus coalgebras, Appl. Categor. Struct. 16(1-2), 255–295 (2008)CrossRefGoogle Scholar
30.Wolff, H., V-Localizations and V-monads, J. Algebra 24, 405–438 (1973)CrossRefGoogle Scholar