Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Wendt, Matthias
2011.
Rationally trivial torsors in -homotopy theory.
Journal of K-theory,
Vol. 7,
Issue. 3,
p.
541.
Morel, Fabien
2012.
A1-Algebraic Topology over a Field.
Vol. 2052,
Issue. ,
p.
81.
Morel, Fabien
2012.
A1-Algebraic Topology over a Field.
Vol. 2052,
Issue. ,
p.
15.
Morel, Fabien
2012.
A1-Algebraic Topology over a Field.
Vol. 2052,
Issue. ,
p.
149.
Morel, Fabien
2012.
A1-Algebraic Topology over a Field.
Vol. 2052,
Issue. ,
p.
199.
Morel, Fabien
2012.
A1-Algebraic Topology over a Field.
Vol. 2052,
Issue. ,
p.
1.
Morel, Fabien
2012.
A1-Algebraic Topology over a Field.
Vol. 2052,
Issue. ,
p.
177.
Morel, Fabien
2012.
A1-Algebraic Topology over a Field.
Vol. 2052,
Issue. ,
p.
113.
Morel, Fabien
2012.
A1-Algebraic Topology over a Field.
Vol. 2052,
Issue. ,
p.
209.
Morel, Fabien
2012.
A1-Algebraic Topology over a Field.
Vol. 2052,
Issue. ,
p.
49.
Vavilov, N. A.
and
Stepanov, A. V.
2013.
Linear groups over general rings. I. Generalities.
Journal of Mathematical Sciences,
Vol. 188,
Issue. 5,
p.
490.
Apte, Himanee
and
Stepanov, Alexei
2014.
Local-global principle for congruence subgroups of Chevalley groups.
Open Mathematics,
Vol. 12,
Issue. 6,
Asok, Aravind
and
Fasel, Jean
2014.
A cohomological classification of vector bundles on smooth affine threefolds.
Duke Mathematical Journal,
Vol. 163,
Issue. 14,
Stavrova, A.
2014.
Homotopy invariance of non-stable K1-functors.
Journal of K-Theory,
Vol. 13,
Issue. 2,
p.
199.
Hazrat, R.
Stepanov, A. V.
Vavilov, N. A.
and
Zhang, Z.
2014.
The Yoga of Commutators: Further Applications.
Journal of Mathematical Sciences,
Vol. 200,
Issue. 6,
p.
742.
Choudhury, Utsav
2014.
Connectivity of motivic H–spaces.
Algebraic & Geometric Topology,
Vol. 14,
Issue. 1,
p.
37.
Ivorra, Florian
2016.
Perverse, Hodge and motivic realizations of étale motives.
Compositio Mathematica,
Vol. 152,
Issue. 6,
p.
1237.
Voelkel, Konrad
and
Wendt, Matthias
2016.
On A1-fundamental groups of isotropic reductive groups.
Comptes Rendus. Mathématique,
Vol. 354,
Issue. 5,
p.
453.
Stavrova, Anastasia
2016.
Non-stable K1-functors of Multiloop Groups.
Canadian Journal of Mathematics,
Vol. 68,
Issue. 1,
p.
150.
Hazrat, R.
Vavilov, N.
and
Zhang, Z.
2017.
The Commutators of Classical Groups.
Journal of Mathematical Sciences,
Vol. 222,
Issue. 4,
p.
466.
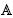 1-Homotopy of Chevalley Groups
1-Homotopy of Chevalley Groups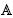 1-homotopy groups of a simply-connected Chevalley group G; these sheaves can be identified with the sheafification of certain unstable Karoubi-Villamayor K-groups.
1-homotopy groups of a simply-connected Chevalley group G; these sheaves can be identified with the sheafification of certain unstable Karoubi-Villamayor K-groups.

