A problem worthy of attack,
Proves its worth by fighting back.
Piet HeinIntroduction
Positive-degree-day (PDD) models, which relate melt to the accumulated total of positive daily temperatures, have been used for ∼100 years. Most of them now use temperature from a weather station near the glacier and estimate the glacier-average summer balance, B s. In a very intensive study, Reference HockHock (1999) applied a PDD model at each of ∼50 locations on Storglaciären, Sweden, where ablation was measured, using temperature from three automatic weather stations on the glacier.
Although PDD models are widely viewed as crude, embodying less-explicit representations of energy transfer processes, their accuracy is comparable with more detailed energy-balance models (Reference HockHock, 2003). Reference OhmuraOhmura (2001) explains that the temperature term is highly relevant, being a measure not only of sensible heat but also of downwelling longwave radiation. Together they ‘account for three quarters of the entire energy source for melt’ and ‘wind speed is only weakly correlated with melt rate’. Although solar radiation might be the largest energy source, the sensible heat flux is more variable temporally, so ablation is better correlated with temperature than with radiation (Reference BraithwaiteBraithwaite, 1981). In field studies of Aletschgletscher, Swiss Alps, Reference Lang and BraunLang and Braun (1990) found that temperature, T, ‘observed at a snow-free valley station, 60 km far from the glacier, provides more information about daily variations of melt rates at the glacier surface than T observations made nearby’.
Nearly all published mass-balance measurements at discrete points on a glacier are distributed by altitude. The definitive archive of measurements, from numerous glaciers over several years, is maintained by the World Glacier Monitoring Service (e.g. Reference Haeberli, Zemp, Frauenfelder, Hoelzle and KääbWGMS, 2005). Moreover, point values of summer balance, b s, vary more rapidly in the vertical direction than in the horizontal. In this paper, spatial variation of the distributed model is in terms of altitude, z.
Temperature in the free atmosphere is used here instead of that from weather stations. Previous analyses estimated B s from temperatures in the US National Centers for Environmental Prediction (NCEP)/US National Center for Atmospheric Research (NCAR) reanalysis database for glaciers in western North America (Reference Rasmussen and ConwayRasmussen and Conway, 2004), in Scandinavia (Reference Rasmussen and ConwayRasmussen and Conway, 2005), in Iceland (Reference RasmussenRasmussen, 2005) and in Svalbard (Reference Rasmussen and KohlerRasmussen and Kohler, 2007).
The main purpose of this paper is to investigate the applicability of upper-air temperatures to modelling summer balance over a range of altitudes. Another objective is to apply the model calibrated over 2003–07 back to the start date (1 January 1948) of that prominent database, by calculating the glacier-average summer balance referred to the 1994 reference topography.
Mount Rainier Mass-Balance Program
US National Park Service staff monitor two of the 27 major glaciers at Mount Rainier National Park (Fig. 1), Washington State. The monitoring program began in 2003 using a multi-scaled approach that incorporates different measurement frequencies. The primary focus is on detailed yearly surface mass-balance monitoring of Emmons and Nisqually Glaciers. Measurement methods used in this program are modifications of procedures that have been used at North Cascades National Park for 16 years (Reference Riedel, Burrows and WengerRiedel and others, 2008) and established during 48 years of research on South Cascade Glacier by the United States Geological Survey Water Resource Division (Reference KrimmelKrimmel, 1996). These methods are similar to those used around the world (e.g. in Norway; Reference Andreassen, Elvehøy, Kjøllmoen, Engeset and HaakensenAndreassen and others, 2005). Glacier monitoring is accomplished during site visits in spring, summer and fall. Internal accumulation has not been determined.

Fig. 1. Emmons, Nisqually, South Cascade and Blue Glaciers. Also shown (open circle) is the gridpoint (47.5° N,122.5° W) from which upper-air temperatures are taken from the NCEP/NCAR reanalysis database and (large closed circle) Longmire, where precipitation is measured.
Emmons Glacier has an altitude range of 1480–4320 m and an area of 11.6 km2, with 2.5 km2 of the lower glacier covered by debris. Nisqually Glacier has an altitude range of 1450–4380 m and an area of 6.9 km2, with 1.2 km2 covered in debris; it includes both the ice-contributing Wilson Glacier and Muir Snowfield. Glacier boundaries were mapped in 1994.
From three to five ablation stakes were placed from year to year on Emmons Glacier ranging from 1700 to 3118 m, making a total of 20 observations. For Nisqually Glacier a total of 16 stakes, from two to four over the years, were placed between 1875 and 3382 m. Initial observations were usually in April at low altitude and as late as late May at high altitude, whilst final observations were in early October at low altitude and as early as mid-September at high altitude.
Summer balance (b s) measurements over 5 years, 2003–07, are shown in Figure 2 for Emmons and Nisqually Glaciers. The mean gradient fit to all five years is 5.17 m km − 1 w.e. at Emmons Glacier and 3.28 m km − 1 w.e. at Nisqually Glacier. In all five years the Emmons Glacier gradient was greater than the Nisqually Glacier gradient by an amount ranging between 1.7 and 3.2 m km − 1 w.e. The mean equilibrium-line altitude over these years was 2800 m at Emmons Glacier and 3250 m at Nisqually Glacier.

Fig. 2. (a, b) Observed 2003–07 summer balance, b
s, versus altitude, z, on (a) Emmons Glacier and (b) Nisqually Glacier. The heavy line is the best-fitting straight line for that glacier, and the light line is the best-fitting line for the other glacier. (c, d) Model results,
![]() versus b
s for (c) Emmons Glacier and (d) Nisqually Glacier. The lines are where
versus b
s for (c) Emmons Glacier and (d) Nisqually Glacier. The lines are where
![]() .
.
Climate
Western Washington has mild, wet winters and mild, dry summers. Temperature and precipitation measurements have been made daily by the National Park Service at Longmire (Fig. 1), which is at 842 m altitude 12 km south-southwest of the summit of Mount Rainier. Over 1948–2007 the mean annual precipitation was 2100 mm w.e., of which 56% fell during the four wettest months, November–February, and 14% during the four driest, June–September. Nearly all precipitation in the region is produced by extratropical cyclones from the Pacific Ocean, 180 km to the west, which often occur in rapid succession in winter and only occasionally in summer. Convective storms are uncommon even in summer.
The mean direction of moisture advection is from the west-southwest (Reference Hayes, Rasmussen and ConwayHayes and others 2002), which puts Emmons Glacier in the lee of the mountain. Two weather stations ∼10 km from the mountain on the lee side receive ∼70% as much precipitation as Longmire.
Upper-Air Data
NCEP/NCAR reanalysis data (Reference KalnayKalnay and others, 1996; Reference KistlerKistler and others, 2001) give values of meteorological variables at many levels in the atmosphere at 10 512 gridpoints, spanning the entire globe at integral multiples of 2.5° in both latitude and longitude. The database has the advantages that it has 6 hour temporal resolution, is free from missing values and is maintained as an integral part of an ongoing major scientific enterprise.
The nearest gridpoint (47.5° N, 122.5° W) is 90 km northwest of Mount Rainier (Fig. 1). Daily data there for 1948–2007 at six standard levels were downloaded in December 2007 from Columbia University (http://ingrid.ldgo.columbia.edu/SOURCES/.NOAA/.NCEP-NCAR/.CDAS-1/). The levels are 1000, 925, 850, 700, 600 and 500 hPa. Their altitudes (geopotential heights) depend on the temperature of the atmosphere between the level and the ground, and can vary by a few percent. They are approximately at 100, 800, 1400, 3000, 4200 and 5600 m.
The next-nearest gridpoint (47.5° N, 120.0° W) is 150 km northeast of Mount Rainier. Not only is it farther away, it is also on the opposite side of the Cascade Mountains, which are a substantial climate barrier in the region. Nevertheless, upper-air temperatures are slowly varying spatially, so the choice of gridpoint is not critical, as shown by Reference Rasmussen and ConwayRasmussen and Conway (2005) for the case of estimating summer balance in Scandinavia.
Seasonal variation of the 1948–2007 mean,
![]() , of temperature interpolated at 3000 m is shown in Figure 3, along with the mean 1948–2007 Longmire precipitation, P, for each calendar month. Figure 3 also shows the received solar radiation under clear skies (atmospheric transmittance 0.8) at 3000 m on each glacier, taking into account the orientation of the glacier surface there. Except for the lowest part of Nisqually Glacier, there is little shading on this nearly conical topography.
, of temperature interpolated at 3000 m is shown in Figure 3, along with the mean 1948–2007 Longmire precipitation, P, for each calendar month. Figure 3 also shows the received solar radiation under clear skies (atmospheric transmittance 0.8) at 3000 m on each glacier, taking into account the orientation of the glacier surface there. Except for the lowest part of Nisqually Glacier, there is little shading on this nearly conical topography.

Fig. 3. Mean climate conditions. (a) Mean 1948–2007 daily mean temperature at 3000 m at 47.5° N, 122.5° W. (b) Mean 1948–2007 monthly precipitation at Longmire. (c) Daily clear-sky insolation, Q, at ∼3000 m altitude on each glacier, assuming atmospheric transmittance 0.8.
A Degree-Day Model
Following Reference De Woul and Hockde Woul and Hock (2005), the model estimate,
![]() , of summer balance at a particular altitude, z, is assumed to be linearly related to temperature according to
, of summer balance at a particular altitude, z, is assumed to be linearly related to temperature according to

in which T + = max(0, T) and the sum over t 1 ≤ t ≤ tn , when the observed summer balance b s(z) was measured, is referred to as the positive-degree-day total, PDD. The regression coefficients, α and β, are chosen to minimize the root mean square (rms) of the model error
In Equation (1) the same coefficients, α and β, are used at all z in all years: α = −6.94 and −4.35 mm °C − 1 d − 1 for Emmons and Nisqually Glaciers, respectively, along with respective β values +1.46 and −0.85. A fortunate property of the regression is that model error, ∊(z), is poorly correlated with z. Correlation coefficients are r = −0.09 for Emmons Glacier and r = −0.04 for Nisqually Glacier. As shown in Figure 2, ∊ correlates poorly with b s itself, so it correlates poorly with z.
Over the 5 years, t 1 ranged between day 90 and day 112 at low altitude and between 94 and 144 at high altitude; respective ranges of tn were between 275 and 287 at low altitude and 255 and 299 at high altitude. Temperature is interpolated at z in the NCEP/NCAR upper-air database. Typical vertical profiles of T and PDD are shown in Figure 4. Use of the upper-air database avoids making assumptions about temperature lapse rates, as is necessary when using temperatures from a weather station at low altitude. Although both b s(z) and T(z) are nearly linear, that is an insufficient condition for the success of the model; rather, the condition is that over the z range of observations, b s is nearly proportional to PDD.

Fig. 4. April–September 2004 temperature profiles at 47.5° N, 122.5° W, the mean of 183 daily profiles. (a)
![]() (heavy) and
(heavy) and
![]() (light); (b) positive degree-days, PDD (Equation (1)).
(light); (b) positive degree-days, PDD (Equation (1)).
The principal processes represented by the αΣT + term are sensible heat transfer and, especially, downwelling long-wave radiation (Reference OhmuraOhmura, 2001). Because summer balance is the resultant sum of ablation and accumulation, the β term is included to represent accumulation and perhaps other forms of energy transfer, such as solar radiation. Reference Braithwaite and ZhangBraithwaite and Zhang (2000) list values of α found in numerous studies, which invariably found higher values for energy absorbed on an ice surface than on a snow surface.
Temperatures were not measured on the glaciers, but comparison with temperatures measured at another glacier in the region indicated that upper-air temperatures are useful in estimating temperatures at a glacier. At Blue Glacier, 175 km to the northwest (Fig. 1), temperature measured at 2008 m adjacent to the glacier in summer 1991 correlated well (r 2 = 0.73, rms = 2.3°C) with temperature interpolated at that altitude in a radiosonde record at a station 65 km west-northwest of the glacier (Reference Conway, Rasmussen and HayesConway and others, 1995). By contrast, the 2008 m temperature at Blue Glacier correlated poorly (r 2 = 0.19, rms = 4.5°C) with surface temperatures measured at a weather station near the radiosonde station.
Model Characteristics
Results are shown in Figure 2, which compares model estimates,
![]() , with observed data, b
s(z). Numerical values of the regression coefficients are, at first glance, surprising, particularly the difference in the degree-day coefficient, α, between the two glaciers. The α values are within the range of values reported by Reference Braithwaite and ZhangBraithwaite and Zhang (2000) for numerous glaciers in Scandinavia, Iceland, the Alps, New Zealand and Patagonia; for a snow surface, they varied between −5.7 and −3.0 mm °C−1 d−1, and for an ice surface between −9.4 and −5.5 mm °C−1 d−1.
, with observed data, b
s(z). Numerical values of the regression coefficients are, at first glance, surprising, particularly the difference in the degree-day coefficient, α, between the two glaciers. The α values are within the range of values reported by Reference Braithwaite and ZhangBraithwaite and Zhang (2000) for numerous glaciers in Scandinavia, Iceland, the Alps, New Zealand and Patagonia; for a snow surface, they varied between −5.7 and −3.0 mm °C−1 d−1, and for an ice surface between −9.4 and −5.5 mm °C−1 d−1.
Goodness of fit is expressed by the coefficient of determination (Reference BevingtonBevington, 1969):
in which σ is the standard deviation of the b s values over the 5 years 2003–07 (20 values for Emmons Glacier, 16 for Nisqually Glacier) and rms is the root mean square of the corresponding ∊ values (Equation (2)).
The difference in α values is not the result of model uncertainty so much as of the difference in the gradients, db s/dz, of the observed b s (Fig. 2). That is,
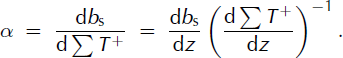
As d ΣT +/dz is approximately the same for both glaciers, differing only because it is determined over slightly different z ranges and slightly different ranges of days for the two glaciers, α is mainly controlled by db s/dz. The Emmons Glacier/Nisqually Glacier ratio of α is 1.60, and of the mean observed db s/dz (5.17/3.28) is 1.58.
There is some year-to-year variation in the model residuals, ∊, which suggests that conditions not strongly correlated with ΣT + exert an effect on b s. For both glaciers, 2004 had strongly negative ∊, 2007 strongly positive. Taking summer precipitation, P s, at Longmire (Fig. 1) as a proxy for insolation, inclusion of a P s term in Equation (1) led to only a slight improvement in the results. For Emmons Glacier r 2 increased from 0.93 to 0.96, and for Nisqually Glacier from 0.87 to 0.90.
The reason why db s/dz differs so markedly between the two glaciers is not as obvious as why α differs between them. One possible explanation is the different aspects of the glaciers, resulting in a large difference in received solar radiation, Q (Fig. 3), which has a weak gradient, dQ/dz. At east-northeast-facing Emmons Glacier, where Q is smaller, the gradient of received energy is dominated by d ΣT +/dz, which is strong; by contrast, at south-facing Nisqually Glacier, where Q is larger, the gradient of received energy has a larger contribution from the weaker dQ/dz. A countervailing effect to the difference in Q is that Nisqually Glacier receives more snowfall than Emmons Glacier, because the advection of moisture is generally from the southwest, so that higher-albedo snow would persist longer into the ablation season at Nisqually Glacier, thus lessening the absorption of Q.
Gradients of linear fits to b s(z) are steeper in years with more negative b s, consistent with the finding of Reference Dyurgerov and DwyerDyurgerov and Dwyer (2000), who analyzed vertical profiles of annual balance for 21 glaciers in the Northern Hemisphere. Over the 5 years, correlation of the gradient, db s/dz, with b s averaged over the profile was r = 0.69 for Emmons Glacier and 0.46 for Nisqually Glacier. Corresponding standard deviations of the gradients were 0.66 and 0.90 m km − 1 w.e.
Reconstructed Summer Balance, 1948–2007
Application of the model (Equation (1)) to 1948–2007 meteorological data creates a
![]() profile for each year, for each glacier. The summation is over the entire year (like Reference De Woul and Hockde Woul and Hock, 2005), but with no contribution from T(t) < 0 during early and late dates. Integrating over the 1994 area–altitude distribution, A(z), of each glacier (Fig. 5) yields a glacier-average summer balance:
profile for each year, for each glacier. The summation is over the entire year (like Reference De Woul and Hockde Woul and Hock, 2005), but with no contribution from T(t) < 0 during early and late dates. Integrating over the 1994 area–altitude distribution, A(z), of each glacier (Fig. 5) yields a glacier-average summer balance:
in which A is the fractional area. For Nisqually Glacier the entire z range is used, but for Emmons Glacier the integration is conducted only up to the altitude where b s(z) = 0, which includes ∼90% of the area. Results for both glaciers over 1948–2007 are shown in Figure 6.

Fig. 5. Area–altitude distributions in 1996 (area per 50 m z interval) and 1948–2007 mean
![]() profiles.
profiles.

Fig. 6. Meteorological conditions 1948–2007. (a) Annual positive degree-days PDD (Equation (1)) at selected altitudes at 47.5° N, 122.5° W. (b, c) Reconstructed summer balance,
![]() , which is integral over the area of Emmons Glacier where
, which is integral over the area of Emmons Glacier where
![]() and over the total area of Nisqually Glacier. (d) Observed 1959–2006 B
s and 1948–58 reconstructed (Reference RasmussenRasmussen, 2009)
and over the total area of Nisqually Glacier. (d) Observed 1959–2006 B
s and 1948–58 reconstructed (Reference RasmussenRasmussen, 2009)
![]() of South Cascade Glacier. Summer balance in m a−1 w.e.
of South Cascade Glacier. Summer balance in m a−1 w.e.
Because hypsometries for previous years are not known for these glaciers, the 1994 area–altitude distributions are used for the entire reconstruction period, yielding the reference-series mass balance suggested by Reference Elsberg, Harrison, Echelmeyer and KrimmelElsberg and others (2001). Thus, the obtained
![]() series contain only climate information, whereas a series obtained by integrating over an evolving glacier topography includes the combined effect of climate and glacier changes. The South Cascade
series contain only climate information, whereas a series obtained by integrating over an evolving glacier topography includes the combined effect of climate and glacier changes. The South Cascade
![]() in Figure 6 is also the reference-series mass balance (Reference RasmussenRasmussen, 2009). Reference Hare and MantuaHare and Mantua (2000) found ∼0.5°C increase in northeast Pacific sea-surface temperature in summer between 1977–88 and 1989–97.
in Figure 6 is also the reference-series mass balance (Reference RasmussenRasmussen, 2009). Reference Hare and MantuaHare and Mantua (2000) found ∼0.5°C increase in northeast Pacific sea-surface temperature in summer between 1977–88 and 1989–97.
A piecewise-constant function is fit to each series in Figure 6 in such a way that the difference between means in consecutive sub-periods is statistically significant. For all three PDD series, the 1985/86 shift is significant at 99% as is the 1967/68 shift at 1500 m; and the 1961/62 shift in PPD at 3500 m is significant at 95%. The shifts in Emmons and Nisqually Glacier B s values mirror this, significant at 99% in 1984/85 and at 95% in 1961/62. At Emmons Glacier, the mean over 1948–61 was more negative than over 1962–84 by 0.52 m a − 1 w.e., and the mean over 1985–2007 was more negative by 0.70 m a − 1 w.e. At Nisqually Glacier the differences were, respectively, 0.24 and 0.39 m a − 1 w.e. At South Cascade Glacier (Fig. 1) the 1986/87 B s shift is significant at 99%.
The mean and standard deviation of
![]() for Emmons Glacier are −3.85 and 0.70 m a
−
1 w.e.; for Nisqually Glacier they are −3.34 and 0.40 m a
−
1 w.e. By comparison, for measured B
s(t) on South Cascade Glacier with altitude range 1650–2100 m, they are −3.28 and 0.60 m a
−
1 w.e.
for Emmons Glacier are −3.85 and 0.70 m a
−
1 w.e.; for Nisqually Glacier they are −3.34 and 0.40 m a
−
1 w.e. By comparison, for measured B
s(t) on South Cascade Glacier with altitude range 1650–2100 m, they are −3.28 and 0.60 m a
−
1 w.e.
The Emmons/Nisqually ratio of the
![]() and α standard deviations are 1.75 and 1.60, respectively. These ratios are controlled through Equation (4) by the Emmons/Nisqually ratio of the mean 2003–07 db
s/dz gradients, which is 1.58.
and α standard deviations are 1.75 and 1.60, respectively. These ratios are controlled through Equation (4) by the Emmons/Nisqually ratio of the mean 2003–07 db
s/dz gradients, which is 1.58.
Discussion
Several factors favor ablation at lower altitude, as reflected by the use in many PDD studies of a larger degree-day coefficient for exposed ice than for a snow-covered surface. The lower-albedo ice surface is exposed for a longer summer period at low altitude than at high. Thus the surface type at low altitude was predominantly ice and at high altitudes it was predominantly snow. The lower albedo of ice enhances absorption of solar radiation (fig. 1 of Reference HockHock, 2003), which prompts use of a larger PDD factor.
More of the ablation at high altitude than at low is due to sublimation, which per quantum of ablation consumes about eight times as much energy as melting does. This is because the air is colder and drier there, with the dew-point temperature often below 0°C (Reference LliboutryLliboutry, 1954; Reference Corripio, Purves, De Jong, Collins and RanziCorripio and Purves, 2005).
Another factor is that summer snowfall is more likely at high altitude than at low, where summer precipitation is more likely to fall as rain. Snowfall restores high albedo and also counteracts mass loss from ablation, both effects making b s less negative.
The foregoing effects would seem to cause a model that uses a single value of the degree-day coefficient, α, to underestimate ablation at low altitudes and overestimate it at high altitudes. Error from such a model would be positive at low altitude and negative at high, so model error would be correlated negatively with altitude. Results from this single-α model for these two glaciers do not have that property.
One countervailing factor is the general increase in global radiation with altitude, which Reference Greuell and SmeetsGreuell and Smeets (2001) ascribe to two effects. Higher albedo leads to multiple reflections between the surface and the atmosphere. There is also generally less horizon obstruction at high altitude. By contrast, they find that variation with altitude in optical path length, water vapor and aerosol content has only a slight effect, although Reference Oerlemans and HoogendoornOerlemans and Hoogendoorn (1989) do find an appreciable increase in atmospheric transmittance with altitude.
A second countervailing factor is that wind transport of any newly falling snow that might occur will generally be down-glacier, making b s more negative at high altitude and less negative below. In other topographic settings, however, higher slopes of a glacier in the lee of a ridge might be a sink for snow blown from the windward side.
Glacier-to-glacier differences in the trend of α with altitude are documented by Reference Zhang, Liu, Xie and DingZhang and others (2006), who found that for some glaciers in western China a increased with altitude and for others it decreased. In the case of the two glaciers on Mount Rainier, it appears that the two sets of factors tend to cancel each other, as demonstrated by the negligibly small correlation between altitude and error in results from the single-α model.
Conclusions
This analysis involves a relatively small number of observations, from only 5 years on only two glaciers in the same region. Temperatures in the free air, obtained from a well-established and -maintained global dataset, afford good estimation of vertical profiles of summer balance. Values of the degree-day coefficient, α, obtained for these two glaciers are within the range of those found in other PDD work over the years, for models that used temperature at a weather station near the glacier to estimate summer balance at individual sites, b s, or averaged over the entire glacier surface, B s.
This analysis with a PDD model using upper-air data yields two striking results. First, whereas it might be expected that a degree-day coefficient varying with altitude might give better results than one that is constant, this is not the case for these glaciers. Second, it is shown that the coefficient is controlled by the vertical gradient in the observed summer balance. Perhaps other analyses will yield further insight into these issues.
Acknowledgements
This work was funded by US National Science Foundation grant OPP-0240861. Comments by A. Arendt, H. Conway, P. Hayes and, especially, scientific editor R. Hock led to a much improved paper.








