Introduction

In recent years, the continuum theory of mixture has been used as the framework for models of natural snow-packs (Reference MorrisMorris, 1983;Reference Akan Akan, 1984;Reference Kelly, Morland and Morris Kelly and others, 1986). The constitutive requirements for such a model are outlined in Reference Kelly, Morland and MorrisKelly and others (1986). These authors pointed out that, if snow is treated as a three-constituent mixture of ice, liquid water and moist air, two volume-fraction equations are required to complete the model. Previous workers have identified only one such equation, an empirical power law relating water content to capillary pressure. This “characteristic” equation for snow is based on very limited data and only applies in conditions of moderate saturation. Thus, to establish a general model for natural snow-packs, it is necessary to extend the range of the empirical characteristic equation and, furthermore, to derive a second volume-fraction equation. This paper uses a theoretical analysis of snow-pack properties on the microscale to derive two volume-fraction equations for conditions of low water saturation, i.e. in the pendular regime.

The mixture theory adopted in the recent snow-melt models is that ofReference Trusdell Truesdell (1965). In this theory, the equations of conservation of mass, momentum, and energy for each constituent within the mixture are expressed in terms of “partial” variables associated with mixture volumes and mixture cross-section areas. Thus, for example, the partial pressure in a particular constituent is defined to be the force on that constituent per unit mixture cross-sectional area. Models are completed by constitutive equations which may also involve “intrinsic” variables which are defined with respect to the volume and cross-section of a particular constituent. For a fully general model for snow, constitutive equations must be specified for the independent volume fractions, the independent phase changes, and for the permeabilities. These equations may be written in terms of partial or intrinsic variables, although it is a fundamental postulate of mixture theory that they should be determined from the gross response of the mixture body. Finally, stress-strain relations for each of the constituents within the mixture model are required. These may be written in terms of intrinsic variables and may be taken as the equations which represent the behaviour of the constituent as if it were an isolated continuum. There is therefore less difficulty in specifying these laws.

A simplification common to many snow models is to treat the air and water vapour as a single constituent. When this is done, a mixture model for snow will have three constituents: ice, water, and moist air. The volume fraction ϕ(ω) is defined as the volume of constituent ω per unit volume of the mixture. We write ω = 1, 2, 3 for ice, water, and moist air, respectively. By definition

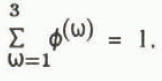
Thus, only two of the volume fractions are independent and only two independent constitutive equations need to be specified.

In the following discussion the intrinsic pressure p(^ω) will be introduced. It is important to establish exactly what is meant by this term in mixture theory. The intrinsic pressure of component ω on the mixture scale is the pressure that would be measured by an instrument which sampled the pressures of a large number of inclusions of ω and averaged them. For example, a tensiometer with a porous cup much larger than the grain-size of the snow would measure p ⁽²⁾. If the inclusions are interconnecting, they all have the same pressure and the intrinsic pressures on the microscopic and mixture-theory scales are the same.

Experimental Data

Reference ColbeckColbeck (1975) andReference Wankiewicz Wankiewicz (1978) have used a simple moisture retention-curve apparatus to determine the characteristic equation for snow. It is worth describing the experimental method in some detail in order to clarify exactly what is being measured and assess the accuracy of the data. In the retention-curve apparatus a column of snow of volume V rests on a porous plate through which water, but not air, can pass. The lower surface of the plate is in contact with water at a pressure p_w. The applied capillary pressure, (where p_a is the atmospheric pressure), can be adjusted by altering the height of a reservoir. A change in height produces a change in applied capillary pressure where ρ is the density of water and g is the acceleration due to gravity.

The amount of water V_w which flows out of the snow sample when is changed is equal to the overflow from the reservoir, which can be measured. Thus, the change in average water content can be determined as a function of . A major assumption is now made, namely, that the intrinsic pressure on the mixture scale of all the water inclusions in the sample is equal to the water pressure applied to the porous plate. In this case, the capillary pressure of the water inclusions with respect to the outside atmosphere, is the same as the applied capillary pressure and is determined as a function of .

In order to derive as a function of , it is necessary to have a direct measurement of at one known value of Reference Wankiewicz Wankiewicz (1979) measured the residual water content at large and negative by a calorimetric method. Alternatively, the relative water saturation can be derived as a function of (Reference ColbeckColbeck, 1975). Assuming that the snow sample is saturated at atmospheric pressure, the required known point is S = 1 at = 0.

Figure 1a shows the data given by Reference WankiewiczWankiewicz (1979). His samples were taken from a natural snow-pack at or near the melting temperature. Figure 1b shows the data given byReference Colbeck Colbeck (1975). The axes have been scaled so the characteristic curves in (a) and (b) should be directly comparable. The curves have a form similar to those obtained by water-retention experiments on coarse-grained sand. The gradient changes between –600 and –1000 Pa when water becomes trapped in the pores.Reference Morrow Harris and Morrow (1964) have found that this transition occurs at for random packings of spheres of radius R₁₃. The interfacial tension between air and water σ₂₃ = 0.075 J m⁻² so that for 1 mm radius grains = -788 Pa. A cubic packing of similar spheres would have = -362Pa and a rhomboidal packing, –968 Pa. The concept of the irreducible water content of snow arises specifically from these water-retention experiments. The water content can of course go to zero in other situations, for example when heat is extracted from the snow sample.

Fig. 1. Characteristic curves for snow derived from water-retention experiments, (a) Reference WankiewiczWankiewicz (1979). (b)Reference Colbeck Colbeck (1975).

Colbeck and Wankiewicz have drawn attention to the difficulties in determining the characteristic equation by this experimental method. Some of these problems also arise when working with soils but others are particular to snow. They may be summarized as follows:

(i) Each data point on the Wankiewicz curves has a potential error of arising from the error in the calorimetric method of determination of the residual water content.

(ii) At applied capillary pressures below about –500 Pa the porous plate loses pressure contact with the bulk of the snow. Thus, is no longer equal to and the long flat tail of the characteristic curves shown in Figure 1 is an artefact of the experimental method.

(iii) Temperature control is obviously vital but it is extremely difficult to maintain truly adiabatic conditions.

Reference ColbeckColbeck (1974) described retention experiments for snow in which the temperature-control problem was solved by using kerosene rather than water. However, these cannot be expected to give an accurate characteristic equation for water in snow. The volume of water at a given capillary pressure depends not only on the geometry of the ice grains (which can be maintained in the kerosene experiments) but also on the surface energies of the phase interfaces. These will not be the same in the ice—kerosene system.

Reference QuervainDe Quervain (1973) gave two water contents at different capillary pressures measured in a natural snow-pack. The authors are not aware of any other published data for snow.

The experimental data were used by Reference Morris and GodfreyMorris and Godfrey (1979) to determine a characteristic equation for use in their snow-melt model. They postulated an equation of the form

where is the capillary pressure of the water inclusions with respect to the moist air inclusions. Equation (2) is one of the Brooks-Corey relationships (Reference Brooks and CoreyBrooks and Corey, 1964) used in modelling the flow of water in unsaturated soils. is the “air-entry potential” or “bubbling pressure” and s is an index of the geometry of the porous medium. Note that in the funicular regime, when the air inclusions are isolated by water and ice from the outside atmosphere, there is no reason why p ⁽³⁾ should equal p_a. However, in the pendular regime of low water content, it is reasonable to assume that the air inclusions form an interconnecting network and p ⁽³⁾ = p _a. Hence in the pendular regime. The index s and the air-entry potential were estimated using all the data from Reference ColbeckColbeck (1975),Reference Wankiewicz Wankiewicz (1979), andReference Quervain de Quervain (1973) with the assumption that throughout the range. The values of have been used byReference Morris Morris (1983) but clearly from the discussion above not all the experimental data points should have been used. If points with high and low water contents are discarded, new values of are obtained (Fig. 2). These are not significantly different because of the large scatter on all the data.

Fig. 2. The empirical power-law characteristic equation determined (a) using all data and (b) discarding data at high and low water contents. The solid lines show the experimental data.

Theoretical Determination of the Volume-Fraction Equations

The primary aim of the theoretical work described in this paper has been to extend the range of the characteristic equation into the pendular regime. The analysis also gives a second volume-fraction equation valid in the pendular regime. This is a useful bonus. Previous models of unsaturated snow-packs have used Equation (2) as one of the required relations and have avoided the problem of identifying a second relation by assuming that the ice-grain velocity is zero. However, this has the important consequence that compaction of the snow cannot be modelled. The identification of a second volume-fraction constitutive equation allows this important physical process to be included in a snow-pack model.

In order to make the theoretical calculations tractable, it is assumed that the ice grains and water in the snow exist in a simple, though still physically realistic geometry. It is supposed that all contacts between ice grains are either simple two-grain contacts with an annular water inclusion or three-grain contacts with three annular inclusions meeting at a vein as described by Reference ColbeckColbeck (1979). The grains are assumed to be spherical, except at the ice—ice and ice-water interfaces. Following Reference GublerGubler (1978), we define end grains with one contact (coordination number n₃ = 1), chain grains with n₃ = 2, and link or mesh grains with n₃ > 2.

We begin with the simple case of a collection of end or chain grains of equal radius and with two-grain contacts. The specific volumes of ice, water, and moist air may be calculated using the geometrical relations shown in Figure 3a, which shows the form of the phase interfaces. The geometry is symmetric about the line FO. For clarity, the figure is not drawn to scale. The radius of the ice-gas interface is R₁₃ = FB = FN. The two radii of curvature of the ice-water interface are = DB and the average value of is given by IJ. The point J is situated such that the arc CJ = BJ. Finally, and are the radii of the water-gas interface; = . The compressed sphere radius is δ = OF and the length ED = a.

Fig. 3. Water inclusions at: fa) two-grain, and (b) three-grain intersections.

The compression angle OAF = ϕ is a measure of the size of the water inclusion and the compression of the grain. The angle α is the dihedral angle, which depends on the surface free energy of the ice-ice interface, σ₁₁. The value of α has been given as 20 ± 10° byReference Ketcham and Hobbs Ketcham and Hobbs (1969) and this is the value used byReference Colbeck Colbeck (1979).Reference Walford, Roberts and Hill. Walford and others (1987) have suggested a value of α = 33.6 ± 0.7° but this is based on 14 measurements and he has subsequently revised the value downwards (personal communication). We expect the value of α to be dependent on the relative crystallographic orientations of the two ice grains. Values of α from 10° to 60° have been measured byReference Ketcham and Hobbs Ketcham and Hobbs (1969).

With the above notation and definitions, it is a straightforward matter to evaluate the volume fractions in terms of the radii of curvature. These calculations are presented in Appendix 1.

To express the volume fractions in terms of the intrinsic pressures, it is necessary to make a physical postulate, namely that the snow mixture is in mechanical equilibrium. In this case, the pressure difference across an interface between constituents is given in terms of the radii of curvature of the interface by the Laplace equations

where σ ₁₂, σ ₁₃, and σ ₂₃ are the interfacial tensions and are taken to be constants with respective values 0.034, 0.109, and 0.075 J m⁻². Note that σ ₁₂ + σ ₂₃ = σ ₁₃. This is required by the geometry which assumes that the contact angle of water on ice is zero. The negative sign in Equation (4) arises because of the saddle shape of the water-air interface. A relation between the various radii is implied by the three Laplace equations, namely

Using the Laplace equations and the geometrical relations established in Appendix 1, it is possible to calculate the volume fractions as a function of the pressure difference ψ, the ice-grain radius R₁₃ , the coordination number n₁₃ (in this case the number of two-grain contacts per grain), and the number of ice grains per unit volume N. The dry density of the snow, ρ_s, is also defined in terms of these variables since

The compression required to achieve mechanical equilibrium limits the number of simple two-grain contacts per grain. For example, three two-grain contacts will interfere unless sin , four contacts will interfere unless sin

, and so on. These high values of sin ø are only found with very low water contents. So, for link grains with n₃ > 2, three-grain intersections must be taken into account. In Appendix 2, expressions for the volume fractions are derived in terms of the radii of curvature for a system of grains of equal radius and contacts between two or between three grains. In this case, the water is held in pendular rings and in veins at three-grain intersections (Fig. 3b).

Equations (3)–(6) may also be applied to this system. Although more complex clusters of grains undoubtedly occur, they will not be included in the model at this stage. In addition, the model does not include water trapped in pores. It thus represents the situation during wetting rather than drying of the snow.

Results

In order to facilitate comparison with the experimental data, the two volume-fraction curves are presented in terms of the water saturation and the (dry) density rather than . Figure 4a shows S as a function of ψ for a density of 300 kg m⁻³, n₃ = 2, and ice-grain radii varying from 0.01 to 1 mm. The solid lines show the water saturation in the pendular regime calculated using the theoretical analysis of the previous section and the Appendices; the best straight line through the experimental data in the pendular—funicular transition region (E) is shown for comparison. The compression angle ø varies from 11.5° at the high saturation end of each theoretical curve to 17.5° at the low saturation end. Figure 4b shows the curves for 0.1 mm grain radius, n₃ = 2, and densities varying from 100 to 500 kg m⁻³. Figure 4c shows the curves for density 500 kg m⁻³, 1 mm grain radius, and coordination numbers from 1 to 4. There are two curves for n₃ = 2, the lower one for a structure with two-grain intersections per grain and the upper one for a structure with one three-grain intersection per grain. For clarity, Figure 4 shows the effect of varying dry density, grain-size, or coordination number while holding the other two parameters constant. This establishes the form of the characteristic curve over a field of values. However, it should be noted that not all combinations of parameter

Fig. 4. Water saturation S as a function of capillary pressure ψ in the pendular regime (a) p_s = 300 kg m⁻³. n₃ = 2. (b) R₁₃ = 0.1 mm. n₃ = 2. (c) p_s = 500kg m⁻³. R₁₃ = 1 mm.

values within the field will be found in real snow. For example, in real snow n₃ will not be independent of p_s .

Although the numerical scheme to calculate the characteristic curve is fairly simple and can easily be incorporated in a snow model, there will be occasions when it is useful to have an approximate analytical expression. The dashed lines in Figure 4 have been calculated using Equation (2), with best values of the parameters s and determined from the theoretical curves. For the ranges p_s = 300–500 kg m⁻³, R₁₃ = 0.01–1.0 mm, and n₃ = 1–4

with

and

The dry density varies approximately as

There is a weak dependence on but this can be neglected. Equation (9) implies that each sphere of ice loses approximately 24% of its volume when it is compressed at a contact. It follows that the equation cannot be extrapolated to n₃ > 4. This is consistent with the initial assumption of non-interfering two- or three-grain contacts which restricts the number of contacts possible per grain. Equations (8) and (9) can be used as the two volume-fraction equations for snow with uniform grain-size and coordination number. The three fundamental variables describing the nature of the snow are the grain-size, coordination number, and number of grains per unit volume. It is assumed that all these can be measured by stereological methods.

The next stage is to define the range of grain-sizes and coordination numbers in a natural snow sample and calculate the appropriate volume-fraction equations. Let the grain-size distribution be given by a log-normal distribution (Reference ColbeckColbeck, 1986)

Reference ColbeckColbeck (1986) has tabulated σ _g and for some saturated snow samples. Mean radius varies from 0.1 to 1 mm and σ _g is 1.4–1.6. The mean grain-size of new dry snow can be much smaller. The probability of finding a grain with diameter less than R ₁₃ is

It will be assumed that, when a grain of diameter R ₁₃ is in contact with another grain of smaller diameter, it produces a “size R ₁₃” inclusion, that is, an inclusion with the size, shape, and capillary pressure that would be produced between two grains of radius R ₁₃. This simple postulate implies that the smaller grain is not in mechanical equilibrium. Reference ColbeckColbeck (1979) has pointed out that ice grains of different sizes in a cluster develop grain boundaries which are curved so that mechanical equilibrium is restored. The smaller grains intrude into the space of the larger grains. At this stage, it is not appropriate to introduce such geometric complexity into the model.

Let the probability of a grain having n ₃ contacts be given by Reference GublerGubler’s (1978) equation

α and i are constants. Reference GublerGubler (1978, fig. 5) has shown p(n₃) for i = 1.5 and α = 0.07636. The mean coordination number is then , a typical value, although n ₃ varied in his samples from 2 to 8. Note that it is assumed that p(n ₃) is independent of R₁₃.

The number of inclusions of size R ₁₃ in contact with grains of radius R ₁₃ is

where n ₃ is the average number of contacts per grain. The total number of size R ₁₃ inclusions is and the total number of inclusions is

Normalizing Equation (13) gives the distribution function for inclusions of size R ₁₃

Figure 5 shows normalized probability densities p(X) and q(X) (in units of for grain-size_and inclusion size. The normalized parameter . As would be expected from the assumption that the larger of a pair of grains controls the inclusion size, the peak of q(X) is shifted to positive values of X.

Fig. 5. Normalized probabilities f(X) for grain-size and q(X) for inclusion size.

The volume fractions are weighted as follows:

In terms of the saturation and density for a uniform sample of N grains, size and coordination number n ₃, the two volume-fraction laws may be written

where the factors K₁, K₂, and K₃ show the effect of variability in the sample and may be calculated from Equations (15) and (16). Table I shows some typical values.

It is apparent that the effect of having a mixture of grain-sizes and coordination numbers is to increase the liquid-water content by a factor of 3–4 above that expected for a uniform sample with the same average properties. Figure 6 shows some example characteristic curves for snow mixtures with

and dry density varying from 100 to 500 kg m⁻³. These wetting curves are now closer to the empirical (drying) curve although still lie below it, as they should, since there is hysteresis in the drying curve.

Fig. 6. Water saturation as a function of capillary pressure in jhe pendular regime for snow with average grain-size . average coordination number and i = 1.

Conclusion

By assuming that the water and ice exist in a particular geometry, we have established, by theoretical means, the two volume-fraction constitutive laws required by three-component mixture models of snow. Thus, for the first time, it is possible to specify a complete three-component mixture model of snow in which the ice-grain velocity is not set to zero and compaction is allowed. However, by specifying a micro-geometry, we are, in a sense, contradicting the philosophical approach of general mixture theory. Mixture theory requires that experiments to determine the constitutive equations should be applied to the mixture as a whole. Clearly, calculations based on simplified geometric assumptions cannot necessarily be expected to give correct results concerning the gross response. There is an urgent need for more experimental data. The advantage of the micro-physical approach is that it is a means, at least in the short term, of completing a general three-phase model which includes all the important physical processes.

Acknowledgements

Part of the work reported in this paper was carried out while R.J. Kelly was supported by a U.K. Natural Environment Research Council Case Studentship, in colloboration with Professor L.W. Morland. We are also grateful to Dr H. GubIer and other members of the Swiss Federal Institute for Avalanche Research for useful discussions.

Appendix 1

In this Appendix, expressions for the volume fractions and in the pendular regime are derived for the simple system in which all ice grains are of equal radius and all contacts are between two grains only, with the geometry shown in Figure 3a. In this case, the coordination number, n₃, is equal to the number of two-grain contacts per grain, n₁ Let the volume obtained by rotating curve HB around the x-axis be denoted by VHB, and so on. Then the volume of ice in unit volume of snow is

where N is the number of grains per unit volume, (VZB - VCB) is the volume of ice lost by a particular grain because of the formation of a two-grain contact, and 2 VZN is the volume of a spherical grain with no contacts, i.e.

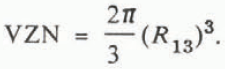
The specific volume of water is

and the specific volume of moist air is

The volumes VCB, VHB, and VZB are calculated as follows: with x- and y-axes set up as in Figure 3a. the equation of the curve ZB is

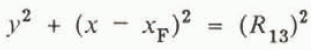
where X_F, y_F are the coordinates of point F.

Hence

The equation of the curve CB is

where

Hence

The equation of the curve HB is

where

Hence

The following geometric relations hold:

Appendix 2

In this Appendix, expressions for the volume fractions are derived for a system of grains of equal size with contacts between two or between three grains. The geometry of a three-grain intersection is shown in Figure 3b. It has features in common with the two-grain intersection shown in Figure 3a and corresponding points are given the same letters. The volume of ice in the three-grain cluster is

where V1 is half the volume of ice in a pair of grains with one two-grain contact, V2 is a 60° segment of a sphere of radius R₁₃, the components of V3 fit together to make half a hexagonal prism with spherical caps, and V4 is the volume of the vein running through the centre of the three-grain cluster. Thus, using the notation of Appendix 1,

and

The radius of the inscribed circle in the hexagonal prism is S and the height of the prism is 2y_c. The spherical caps have radius R ₁₃ and height (R₁₃ – y_c). Thus,

The volume of the vein may be calculated followingReference Nye Nye (1989), who has shown that the area of the asymptotic cross-section of a water vein at a three-grain intersection in polycrystalline ice is where

with β = π/6 – β/2 and r_v is the radius of the ice-water interface. For the case of a three-grain contact in snow, it is assumed that the cross-sectional area of the vein is constant throughout its length which is 2y_c sin γ where the angle γ is given by

Thus, the volume of the vein is

For the purposes of this paper, it is not necessary to make a separate precise calculation of the volume ot a node at each end of the vein. Since the pressure in the vein must be the same as that in the two-grain inclusions which are connected to it and in contact with the same ice grains, the radius of the cylindrical ice-water interfaces of the vein is given by the Laplace equation

The volume of water in the three-grain inclusion is

where V5 is a section of the annular two-grain water inclusion.

Let the number of two- and three-grain contacts per grain be n₁ and n₂ , respectively, arranged in such a way that the inclusions do not interfere. The coordination number n₃ = n₁ + 2n₂.

Then the specific volume of ice is

and the specific volume of water is