Introduction
The rate of Greenland ice sheet mass loss has accelerated throughout the past decade (Reference Rignot, Velicogna, Van den Broeke, Monaghan and LenaertsRignot and others, 2011) due to decreased surface mass balance and increased discharge from marine-terminating outlet glaciers (Reference Van den BroekeVan den Broeke and others, 2009). Outlet glacier retreat and acceleration were concurrent with increased heat transport within Greenland coastal waters, which has been attributed to large-scale changes in ocean circulation and penetration of warm subtropical water carried by the Irminger Current onto the East and West Greenland continental shelves (Reference Holland, Thomas, de Young, Ribergaard and LyberthHolland and others, 2008; Reference StraneoStraneo and others, 2010; Reference ChristoffersenChristoffersen and others, 2011; Reference Seale, Christoffersen, Mugford and O’LearySeale and others, 2011). The increase in warm water delivery to the continental shelves starting in the mid-1990s was linked to the switch of the North Atlantic Oscillation from a strong phase to a weak state, resulting in an increase in the volume of subtropical water entering the Irminger Current (Reference ChristoffersenChristoffersen and others, 2011). These warm waters were then transported along the east and west coasts of Greenland in the East and West Greenland Currents (Reference Holland, Thomas, de Young, Ribergaard and LyberthHolland and others, 2008; Reference StraneoStraneo and others, 2010). At Jakobshavn Isbræ, intermediate-depth coastal waters warmed >1°C throughout the 1990s as a result of the increased transport of subtropical waters in the West Greenland Current (Reference Holland, Thomas, de Young, Ribergaard and LyberthHolland and others, 2008). According to Reference Motyka, Truffer, Fahnestock, Mortensen, Rysgaard and HowatMotyka and others (2011), this warming could have increased submarine melt rates beneath the floating ice tongue by 25%, from 228 m a−1 to 285 m a−1, between the mid-1980s and late 1990s.
Submarine melt rate estimates for Jakobshavn Isbræ provided by Reference Motyka, Truffer, Fahnestock, Mortensen, Rysgaard and HowatMotyka and others (2011) are an order of magnitude higher than the rate of ∼10 m a−1 estimated for Petermann Glacier, northwest Greenland (Reference Rignot and SteffenRignot and Steffen, 2008). Estimates from Reference Motyka, Truffer, Fahnestock, Mortensen, Rysgaard and HowatMotyka and others (2011) are, however, within the estimated melt rate range of 250–1400 m a−1 for the vertical calving faces of several glaciers immediately to the north of Jakobshavn Isbræ from oceanographic observations obtained in August 2008 (Reference Rignot, Koppes and VelicognaRignot and others, 2010). Given the large variability in estimated submarine melt rates for the few Greenland outlet glaciers for which they are available, we hypothesize that submarine melt rates may vary greatly spatially and temporally.
We use multiple remote-sensing datasets and a mass continuity approach similar to that of Reference Motyka, Truffer, Fahnestock, Mortensen, Rysgaard and HowatMotyka and others (2011) to estimate submarine melt rates beneath 13 outlet glacier floating ice tongues in Greenland (Fig. 1). We examine spatio-temporal variations in melt rates since 2000 and compare this variability to changes in glacier front retreat and speed, as well as ocean temperature, to assess potential relationships between external forcing (i.e. ocean heating) and tidewater glacier behavior. We also compare the rate of volume loss from calving (i.e. calving of icebergs and melt along the vertical calving face) and submarine melting beneath the floating ice tongue to the discharge (i.e. ice volume transported per unit time) passing through the grounding line to determine the relative importance of calving and melting for floating ice tongues.

Fig. 1. RADARSAT image mosaic from 2005 overlaid by circles denoting the approximate location and average submarine melt rate for the glaciers included in the study. Regional Moderate Resolution Imaging Spectroradiometer (MODIS) sea-surface temperature (SST) data were extracted from the locations indicated by the five thick white lines, which are referred to as north (N), northwest (NW), west (W), southeast (SE) and east (E) in the text. Glaciers are Petermann (P), Yngvar Nielson (YN), Edvard (E), Docker Smith (DS), Kong Oscar (KO), Alison (A), Upernavik North (UN), Rink (R), Jakobshavn Isbræ (JI), Helheim (H), Midgard (M), Kangerdlugssuaq (K) and Daugaard Jensen (DJ). Background image courtesy of I. Joughin, University of Washington.
Data Collection and Methods
We estimated the average submarine melt rate for each glacier tongue as the difference in the discharge through cross sections at the grounding line and near the ice front, divided by the surface area of the ice tongue between the cross sections, minus the estimated volume of surface melt and run-off. Our estimates were also corrected for thinning due to convergence or divergence between the cross sections, which would result in thickness changes without any change in ice volume. Discharge values were obtained from remotely sensed ice flow velocity and thickness. Surface mass-balance rates were obtained from a coupled meteorological and surface energy-balance reanalysis model. Details of these observations are provided in this section.
Measurement locations, speed and ice thickness
For each glacier we mapped a time series of front position from Landsat 7 Enhanced Thematic Mapper Plus (ETM+) panchromatic band and Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTER) visible/nearinfrared (VNIR) satellite imagery. Both sensors provide a 15 m pixel resolution and have a nominal repeat interval of 16 days, although ASTER only acquires imagery on demand, and thus provide only a few images of each glacier per season.
Surface elevations mapped by (1) stereoscopic 30 m resolution ASTER digital elevation models (DEMs) from 2000 to 2010, (2) 40 m resolution SPOT-5 (Système Pour l’Observation de la Terre) DEMs from 2007 to 2008 distributed by the SPIRIT (SPOT-5 stereoscopic survey of Polar Ice: Reference Images and Topographies) program (Reference Korona, Berthier, Bernard, Rémy and ThouvenotKorona and others, 2009), and (3) airborne lidar data obtained by the NASA Airborne Topographic Mapper (ATM) were used to calculate mean melt-season surface elevation profiles along the center line of each glacier. Using these data and surface speed measurements (described below), grounding line positions were identified by distinct breaks in the along-flow surface slopes and decreases in longitudinal strain rates, indicating a change to flotation. Grounding lines were located for each year with available data in order to account for changes in position. Using this technique, our grounding line locations may be biased seaward of the true grounding line (i.e. the seaward limit where ice first loses contact with the bed), in the zone of flexure associated with the transition from grounded to floating ice (Reference Brunt, Fricker, Padman, Scambos and O’NeelBrunt and others, 2010). We estimate the uncertainty associated with this technique by comparing the estimated grounding line positions to those obtained from ice-penetrating radar (discussed below) for the four glaciers where such data were available. These positions agreed within 300 m of the positions identified from surface slope and speed gradients, with a negligible impact on our results.
Time series of surface speeds within ±1 km of the center line at each measurement location were obtained using IMMATCH/MIMC Repeat Image Feature Tracking (RIFT) software distributed by the Glacier Dynamics Group at The Ohio State University. A full description of the error assessment and validation of the software is provided by Reference Ahn and HowatAhn and Howat (2011). The number of surface speed observations obtained from the feature-tracking software varied spatially and temporally with availability of cloud-free ETM+ and ASTER VNIR satellite imagery obtained during the melt season. Speed measurements were only available during the melt season (typically April–September), when identifiable surface features could be tracked by the feature-tracking algorithm. False-correlation outliers were manually removed prior to calculating the annual median, mean and standard deviation of the individual speed observations. We found that several annual means were skewed by short-term peaks in speed, so we use the annual median speeds in our discharge calculations. To characterize the temporal variability in these observations, we use the standard deviation of speed estimates, hereafter referred to as speed uncertainty. We assume that this measure (mean value 1.2 m d−1) is representative of the typical temporal variability in melt season speeds following outlier removal.
Time series of ice thickness across the front were estimated using the ice surface (freeboard) elevation assuming constant densities of ice (917 kg m−3) and sea water (1028 kg m−3), which impart an uncertainty of ∼±10 m on our thickness estimates (Reference Motyka, Truffer, Fahnestock, Mortensen, Rysgaard and HowatMotyka and others, 2011). Additional ice thickness uncertainty can be attributed to uncertainties in DEM- and ATM-derived elevations, which are estimated as ±5 m following vertical baseline registration and averaging over 25-pixel blocks for the ASTER DEMs (Reference Howat, Joughin, Fahnestock, Smith and ScambosHowat and others, 2008), ±6 m for the SPOT-5 DEMs (Reference Korona, Berthier, Bernard, Rémy and ThouvenotKorona and others, 2009) and ±0.2 m for NASA ATM data (Reference KrabillKrabill and others, 2002). To account for the use of mean melt-season elevations when available, we assume an elevation uncertainty of ±5 m and cumulative thickness uncertainty of ±55 m for all front ice thickness estimates.
For the four glaciers with existing bed topography data at their grounding lines (Table 1) provided by the University of Kansas Center for Remote Sensing of Ice Sheets (CReSIS, https://www.cresis.ku.edu/data), the grounding line location was identified as the point where the draft (i.e. depth below sea level of the base of the ice) calculated from the ice freeboard intersected the CReSIS bed elevation. Annual time series of ice thickness across the grounding line were then calculated by differencing the surface elevations (described above) and the CReSIS bed elevations along a transect perpendicular to ice flow. We assume an average thickness uncertainty of ±35 m due to bed and surface elevation error, as described by Reference Howat, Ahn, Joughin, Van den Broeke, Lenaerts and SmithHowat and others (2011).
Table 1 . Maximum and mean surface melt rates, mean submarine melt rates, melt rate uncertainty, melt rate temporally random error (uncertainty minus systematic error), mean rate of volume loss from calving and melting, and mean grounding line discharge values calculated for the 2000–10 study period. The type of data used to calculate grounding line ice thickness is included in the last column: ice thicknesses were estimated by differencing bed elevation from CReSIS by surface elevations (‘CReSIS’), adjusting inland IceBridge MCoRDS ice thickness data to account for surface mass balance and ice divergence to the grounding line (‘MCoRDS’), and using the ice freeboard to determine the thickness from assumed flotation (‘freeboard’)

Ice thicknesses at the grounding line were estimated for Alison, Docker Smith, Kong Oscar and Yngvar Nielson glaciers using observed ice thickness at cross sections located 1.5–9 km inland. These data are from the 2010 IceBridge MCoRDS (Multichannel Coherent Radar Depth Sounder) dataset provided by the US National Snow and Ice Data Center (NSIDC, http://nsidc.org/data/irmcr2.html). We estimate the thickness uncertainty of ±10 m based on the 4.5 m resolution of the MCoRDS depth measurements and ∼5 m of elevation uncertainty. Grounding line ice thickness, H g, was estimated from the inland thickness data from continuity:

where subscripts i and g denote the inland location and grounding line respectively, Q i is the discharge, M ig and D ig are the volume rates of surface mass balance and ice divergence, respectively, over the area between the inland location and the grounding line, U g is the median surface speed and W g is the glacier width. The volume rate of surface mass balance between the inland location and the grounding line, M ig, was determined from the mean annual surface mass balance (SMB) from the Regional Atmospheric Climate Model v.2 (RACMO2) obtained near the grounding line of each glacier. The ice divergence, D ig, accounts for the deviation from steady-state flow between the inland location and the grounding line and is obtained from
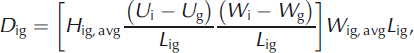
where H ig, avg is the average ice thickness, (U i – U g)/L ig is the speed gradient, (W i – W g)/L ig is the width gradient, W ig, avg is the average width and L ig is the length between the grounding line and inland location. Since both H g and H ig, avg are unknown, we solve Eqns (1) and (2) iteratively, starting with an initial guess for H g obtained from solving Eqn (1) with D ig = 0, and solving for H ig, avg until convergence of H g is achieved. Grounding line thickness uncertainty was calculated using propagation of errors from speed uncertainty and inland thickness uncertainty (listed above), width uncertainty at the inland location and grounding line, and length uncertainty associated with estimation of the grounding line location. We assign a width uncertainty of ±15 m (one pixel) and length uncertainty of 300 m (described above). The mean grounding line thick- ness uncertainty for these data is ±125 m.
For the remaining glaciers, which have limited or no available thickness data, time series of ice thickness across the grounding line were estimated using the ice freeboard (described above). As noted above, the identified grounding line is likely located within the flexure zone where the ice is not yet in hydrostatic equilibrium, which contributes to uncertainty in our ice thickness estimates. The additional sources of error in the grounding line thickness estimate include uncertainty associated with changes in tidal flexure, grounding line identification and surface elevations. Cumulative uncertainty is estimated at approximately ±150 m from a comparison of center-line MCoRDS data with contemporaneous ice thickness estimates using ice freeboard.
Submarine melt rate
Using the ice thickness and speed data described above, we estimated time series of ice discharge, Q, at the grounding line (subscript g) and ice front (subscript f) by multiplying the annual median melt season surface speed by the glacier width and ice thickness at the front and grounding line locations. The sum of submarine and surface melt rates, m, averaged over the length, L gf, and width, W gf, of the floating glacier tongue was then estimated using

where D
gf is the ice divergence along the floating tongue. Ice divergence, D
gf, was calculated using grounding line and front data input into Eqn (2), where ![]() ,
, ![]() and the width and speed gradients were calculated between the grounding line and front. Uncertainties associated with each estimate were calculated using error propagation of the aforementioned speed, thickness, width and length uncertainties.
and the width and speed gradients were calculated between the grounding line and front. Uncertainties associated with each estimate were calculated using error propagation of the aforementioned speed, thickness, width and length uncertainties.
To determine the relative contribution of submarine and surface melt to m, we obtained estimates of summer (June–August) RACMO2 SMB rates near each glacier front. In all cases, the SMB rates are at least two orders of magnitude less than m (Table 1), well within the uncertainty associated with our melt rate estimates.
Sea surface temperatures
Sea surface temperatures (SSTs) surrounding Greenland were obtained from the Moderate Resolution Imaging Spectroradiometer (MODIS) instrument on the Terra and Aqua satellites. Data were obtained from the Physical Oceanography Distributed Active Archive Center (PODAAC, http://podaac.jpl.nasa.gov). In order to characterize regional temporal variability in SSTs, MODIS SST data were obtained from the average of 20 gridcells (0.083° × 0.083° resolution) at each of the five offshore locations identified in Figure 1. Mean melt season (May–September) SSTs for 2000–10 were calculated from monthly means. SSTs are shown as anomalies relative to their 2000–10 means.
Results
We are able to derive an average of four melt rate estimates for each glacier from 2000 to 2010. Time series of annual melt season submarine melt rates are presented in Figure 2. Data are divided geographically to examine differences in submarine melt rates relative to observed contemporaneous changes in dynamics, as described by Reference Howat, Joughin, Fahnestock, Smith and ScambosHowat and others (2008) for southeast Greenland and Reference McFadden, Howat, Joughin, Smith and AhnMcFadden and others (2011) for west Greenland.

Fig. 2. Annual melt season submarine melt rate time series for East (a) and West (b) Greenland marine-terminating outlet glaciers with floating termini. Error bars indicate temporally random error in the melt rate estimates (Table 1, column 6).
The mean submarine melt rate from 2000 to 2010 varied from a minimum of 0.03 ± 0.02 m d−1 at Petermann Glacier to a maximum of 2.98 ± 0.65 m d−1 at Jakobshavn Isbræ (Table 1). There was no significant difference between mean submarine melt rates in east Greenland (1.09 ± 0.57 m d−1)) and west Greenland (1.13 ± 0.44 m d−1),, nor do we resolve a regionally consistent change over the study period.
We determine the significance of interannual variability in submarine melt rates for each glacier by examining the annual melt rates relative to the temporal mean. We assume that the interannual variability in the submarine melt rate is significant if the departure from the mean exceeds the temporally random error. The temporally random error (Table 1, column 6) is calculated by removing the systematic error (i.e. error in estimated ice thickness from associated elevation uncertainty) from the submarine melt rate uncertainty described above (Table 1, column 5). Using this criterion, Jakobshavn Isbræ, Kong Oscar, Upernavik North and Daugaard Jensen had significant interannual variability. The magnitude and timing of changes in melt rates, however, varied considerably between glaciers. For both Daugaard Jensen and Upernavik North, melt rates varied by a factor of 2 during their time series, with peak melt rates occurring in 2006. The submarine melt rate for Jakobshavn Isbræ increased considerably, with an increase from 2.14 ± 0.18 m d−1 to 3.81 ± 0.49 m d−1 (+78%) from 2002 to 2003. Between 2000 and 2005, Kong Oscar’s melt rate increased by a factor of 7, the largest increase in our dataset.
Changes in mean annual front position are shown in Figure 3a and b, and median annual grounding line speeds are shown in Figure 4a and b. From 2000 to 2010, 9 of 13 glaciers retreated >1 km, with a maximum retreat of 13.6 km at Jakobshavn Isbræ. Within the study period, noticeable acceleration occurred for 6 of the 8 glaciers that underwent >4 km of retreat, while acceleration of the remaining glaciers did not exceed the measurement uncertainty. Overall, interannual variability in submarine melt rates was uncorrelated with the magnitude of retreat or acceleration for each glacier (Table 2).

Fig. 3. Mean annual front retreat relative to the 2000 front position for East (a) and West (b) Greenland.

Fig. 4. Median annual grounding line speed for East (a) and West (b) Greenland. Speed error bars indicate ±1 standard deviation from the mean speed following the removal of false correlation outliers.
Table 2. R 2 values (p-values) from correlation analysis for the glaciers with >3 years of submarine melt rate, front position and speed data. The correlation coefficients for each variable (i.e. retreat, speed and SST) were calculated with respect to changes in the submarine melt rate for each glacier

Time series of MODIS melt season (May–September) SST anomalies from the regions specified in Figure 1 are presented in Figure 5. Anomalously high ocean temperatures on the southeast Greenland continental shelf in 2003 (Reference Howat, Joughin, Fahnestock, Smith and ScambosHowat and others, 2008; Reference MurrayMurray and others, 2010), which exceed the ±0.4°C MODIS SST uncertainty, are evident in the east (+2.1σ) and southeast (+1.1σ) regions. Positive SSTanomalies are also noted in the west (+0.9σ), and northwest (+1.2σ) regions in 2003. The 2010 positive SST anomalies exceed the 2003 anomalies for all regions except the east. According to our significance criterion described above, we find that the 2003 positive SST anomaly is contemporaneous with a significant increase in submarine melt rates from 2002 to 2003/04 at Jakobshavn Isbræ, Kong Oscar and Daugaard Jensen. The 2010 positive SST anomaly is not, however, contemporaneous with an increase in the submarine melt rates for three of the four glaciers with 2010 data.
Discussion
Our submarine melt rate estimates are similar to those derived from in situ measurements by Reference Rignot and SteffenRignot and Steffen (2008) for the Petermann Glacier floating tongue and the melt rates along the vertical calving faces of glaciers in the Disko Bay region determined by Reference Rignot, Koppes and VelicognaRignot and others (2010). We estimate an annual melt rate of ∼10 m a−1 averaged over the length of the Petermann tongue, which is within the along-flow profile range of ∼1–25 m a−1 obtained by Reference Rignot and SteffenRignot and Steffen (2008). Although we cannot directly compare our submarine melt rates from beneath floating termini to the calving-face melt rates calculated by Reference Rignot, Koppes and VelicognaRignot and others (2010), the three closest glaciers for which we have estimates (Jakobshavn Isbræ, Rink and Upernavik North glaciers) all fall within the 0.7 ± 0.2 m d−1 to 3.9 ± 0.8 m d−1 range observed by that study.
A comparison of the submarine melt rate data in Figure 2a and b with the ocean temperature time series (Fig. 5) suggests a possible relationship between submarine melt rates and changes in mean melt-season MODIS SSTs. However, correlations between time series of melt rates and ocean temperature are not statistically significant and the sample size is too small to provide detailed analysis or meaningful statistics regarding relationships between the available data.
Since the vertical area of the calving face below the waterline is typically small relative to the area of the tongue or ice shelf, melting along the calving face is likely to fall within the error of the total volume loss from submarine melting. Therefore, we assume that the discharge at the front approximates the calving rate, but note that the calving rate presented herein is composed of volume loss from calving of icebergs, and unknown but potentially large volume loss from melt along the vertical calving face. Using this estimated calving rate, we examine the relative contributions of submarine melting, calving and discharge across the grounding line (Fig. 6; Table 1). Submarine melting along the base of floating termini accounts for 5–85% of the grounding line discharge, averaging 43% over the study period. There are no trends in the ratio of melting to calving with latitude nor is there a distinct difference between east and west glaciers. The fraction of volume lost due to calving is largest for Kangerdlugssuaq and Helheim glaciers in the southeast. We note, however, that discharge estimates for these glaciers are based on data collected during a single year of abnormally high ice discharge following extensive retreat (Reference Howat, Joughin and ScambosHowat and others, 2007, Reference Howat, Ahn, Joughin, Van den Broeke, Lenaerts and Smith2011), which may yield unrepresentatively high calving rates. At the other end of the spectrum, Daugaard Jensen glacier has an anomalously low ratio of calving to melting, which may be related to the glacier’s high seasonal variability in front position and speed (Reference Walsh, Howat and Ahn Yand EnderlinWalsh and others, 2012). With the exception of these end members, the percentage of volume loss from melting falls within the range 35–75%, consistent with the observations of Reference Rignot, Koppes and VelicognaRignot and others (2010). There is, however, a large amount of temporal variability, with most glaciers varying over 48% about the mean ratio of calving to melting. We found that temporal variability in the ratio of calving to melting is not correlated with changes in floating tongue length for the glaciers with multi-year records (not shown), suggesting that front retreat does not significantly impact the ratio of melting and calving for floating ice tongues.

Fig. 6. The mean ratio of volume loss from melting versus calving (i.e. calving of icebergs plus melting along the vertical calving face) relative to the grounding line discharge for the 13 glaciers analyzed in this study. Error bars indicate the range in melting and calving fractions for each glacier over the observation period. Triangle (square) symbols denote East (West) glaciers. Colors indicate relative glacier latitude, with darker red (blue) indicating lower (higher) latitudes.
The anomalously high ratios of calving to melting observed at Helheim and Kangerdlugssuaq glaciers during their speed-up events suggests that calving rates may increase with discharge across the grounding line, while melt rates are independent of grounding line discharge. We test this hypothesis by examining changes in calving rate and grounding line discharge for each glacier with ≥4 years of measurements. For each glacier, we divide the calving rate and discharge estimates by their respective means and apply a linear regression to plots of the data (Fig. 7). While the small number of data points makes this analysis inconclusive, the relationship between calving rate and grounding line discharge is statistically significant at the 95% confidence level (as determined from a one-tailed t-test) for Alison, Petermann, Rink and Upernavik North. Of these, all show a positive trend in calving with discharge, except Petermann. The anomalous trend for Petermann is, however, the result of temporal variability in the assigned calving front location used to calculate front discharge due to the substantial noise in surface elevations from advection of large-wavelength undulations in the surface, which causes artificial temporal changes in the calving rate.

Fig. 7. The rate of volume loss from calving (i.e. rate of volume loss from the calving of icebergs plus melting along the vertical calving face) versus the grounding line discharge divided by their respective mean values for all glaciers with ≥4 years of measurements. The axes scales in the lower left subplot apply to all subplots. The R 2 value in the lower right corner of each subplot is for the linear regression (thin black line) applied to each glacier.
Conclusions
Using remotely sensed data, we estimated time series of submarine melt rates beneath 11 floating glacier tongues in Greenland from 2000 to 2010. On average, melt rates ranged from 0.03 ± 0.02 m d−1 to 2.98 ± 0.65 m d−1, with no clear spatial pattern. Four glaciers (Jakobshavn Isbræ, Kong Oscar, Upernavik North and Daugaard Jensen) showed significant interannual variability in melt rates, but changes in melt rates were uncorrelated with changes in ice dynamics. Changes in submarine melt rates for these glaciers were also uncorrelated with changes in regional ocean temperatures, although the short time series prevents conclusive analysis of the significance of any relationship between these variables. Furthermore, our estimated submarine melt rates indicate that the percentage of volume loss from submarine melting beneath floating ice tongues ranged from 5% to 85%, with an average value of 43% from 2000 to 2010. Our data also suggest that, for most glaciers, grounding line discharge and submarine melt rates vary independently but that calving may increase with discharge. While the small sample size, low temporal resolution and large uncertainty of our measurements prevent conclusive assessment of the relationship between oceanographic forcing and glacier response, our results highlight the high degree of spatial and temporal variability in glacier submarine melt rates and the need for expanded observations of fjord ocean conditions and ice– ocean interactions.
Acknowledgements
We thank our two anonymous reviewers for insightful comments that greatly improved the manuscript. This work was funded by a NASA Earth and Space Science Fellowship to E.M.E.












