1. INTRODUCTION
The first successful numerical approach to modeling ice-sheet flow and geometry evolution in two horizontal dimensions was the classical finite difference (FD) scheme introduced by Mahaffy (Reference Mahaffy1976). This scheme numerically solves the shallow-ice approximation (SIA; Hutter, Reference Hutter1983) by computing the ice flux at staggered-grid points using particular choices when evaluating the ice thickness and surface slope. An advantage of the scheme is its relatively small stencil, which reduces memory access in implicit or semi-implicit implementations (Hindmarsh and Payne, Reference Hindmarsh and Payne1996). It also reduces interprocess communication when implemented in parallel.
However, existing numerical models solve the time-dependent SIA using explicit or semi-implicit time-stepping (Hindmarsh and Payne, Reference Hindmarsh and Payne1996; Huybrechts and others, Reference Huybrechts1996; Bueler and others, Reference Bueler, Lingle, Kallen-Brown, Covey and Bowman2005; Egholm and Nielsen, Reference Egholm and Nielsen2010; Jarosch and others, Reference Jarosch, Schoof and Anslow2013). Time-stepping restrictions are required in that context to avoid classical instabilities at wavelengths comparable with the grid spacing (Morton and Mayers, Reference Morton and Mayers2005). However, Bueler and others (Reference Bueler, Lingle, Kallen-Brown, Covey and Bowman2005) and Jarosch and others (Reference Jarosch, Schoof and Anslow2013) point out that these schemes also involve ad hoc treatment of the free margin of the ice sheet, for example using projection to reset computed negative thicknesses back to zero. It would be desirable to escape both time-stepping restrictions and model the margins in a mathematically principled manner. Both the goals are achievable if one implicitly solves the SIA as a free-boundary problem.
Early work on the free-boundary problem in one horizontal dimension (Hindmarsh and others, Reference Hindmarsh, Morland, Boulton and Hutter1987) avoided ad hoc margin treatment by tracking it as a moving grid point. However, such margin-tracking does not easily extend to two dimensions (2D) because the margin of a real ice sheet is a curve of minimal smoothness and unknown-in-advance topology. Calvo and others (Reference Calvo, Durany and Vázquez2000, Reference Calvo, Díaz, Durany, Schiavi and Vázquez2002) describe the time-dependent free-boundary problem as a parabolic complementarity problem, including the constraint that ice thickness is never negative, but their work is limited to one horizontal dimension and flat bed. They also solve each time step numerically by a projected Gauss–Seidel scheme (Ciarlet, Reference Ciarlet2002), which does not scale to large problem sizes.
Jouvet and Bueler (Reference Jouvet and Bueler2012) pose and numerically solve the steady-state free-boundary problem as a variational inequality (Kinderlehrer and Stampacchia, Reference Kinderlehrer and Stampacchia1980) in two spatial dimensions and with non-trivial bed topography. Because this variational inequality is not equivalent to a minimization problem, in the general (non-flat-bed) case, they solve it by iterating well-posed but only approximate minimization problems that converge to the full equations in a fixed-point limit. The success of this method is demonstrated in a 5 km resolution steady-state calculation for Greenland using a piecewise-linear triangulation finite element (FE) method (Elman and others, Reference Elman, Silvester and Wathen2005). In related work, Jouvet and Gräser (Reference Jouvet and Gräser2013) solve the SIA component of their time-stepping hybrid ice dynamics model (Winkelmann and others, Reference Winkelmann2011) through a sequence of minimization problems that use the thickness from the previous time step. Each minimization problem is solved by a constraint-adapted nonlinear multigrid Newton iteration.
This paper follows Jouvet and Bueler (Reference Jouvet and Bueler2012) by solving the steady-state free-boundary problem, but it uses a Mahaffy-like scheme on a structured rectangular mesh, and applies the Newton iteration directly to the SIA equations. A continuation scheme generates an iterate within the domain of convergence of the Newton method, which then exhibits quadratic convergence. We formulate the discrete problem as a nonlinear complementarity problem (Benson and Munson, Reference Benson and Munson2006) and solve it in parallel using either of two solvers from the open-source PETSc library (Balay and others, Reference Balay2015). Because we have successfully solved the whole free-boundary problem all at once, our improved scheme is unconditionally stable as a fully implicit scheme, at least when the bed is not too rough.
The first part of this paper has a historical side. We reinterpret the classical Mahaffy scheme as using a non-standard quadrature choice in the conservation-of-mass flux integral. In this reinterpretation the approximate ice thickness lives in a continuous space of trial functions, unlike in the original FD scheme. These trial functions are piecewise-bilinear on a structured grid of rectangles, that is, they are Q 1 FEs (Elman and others, Reference Elman, Silvester and Wathen2005). Our reinterpretation has both finite volume (FV; LeVeque, Reference LeVeque2002) and FE aspects. It is natural to call the scheme a ‘finite volume element’ method (FVE; Cai, Reference Cai1990; Ewing and others, Reference Ewing, Lin and Lin2002) because the weak form is simply the flux integral itself. Adopting FVE thinking gives the best of both (i.e. FE and FV) worlds from the point of view of understanding the parts of the scheme.
This paper is organized as follows. Starting with a statement of the steady, isothermal SIA model, the classical Mahaffy scheme is recalled and then reinterpreted. Better quadrature in the flux integral, and a bit of first-order upwinding on the part of the flux that comes from the bedrock slope, are then added. The resulting improved scheme, which has the same stencil as the classical Mahaffy scheme, is called ‘
![]() ${M^{\rm \star}} $
’. The Newton solver for the discrete equations and constraints is then introduced. Initial numerical results in verification cases are excellent for a flat-bed dome exact solution and better than those from published higher-resolution upwind schemes on a bedrock-step exact solution. Then the method is applied to a real ice sheet by computing the steady-state shape of the Greenland ice sheet in a present-day modeled climate, at high resolution including sub-kilometer grids. An Appendix addresses the analytical calculation of the Jacobian in the
${M^{\rm \star}} $
’. The Newton solver for the discrete equations and constraints is then introduced. Initial numerical results in verification cases are excellent for a flat-bed dome exact solution and better than those from published higher-resolution upwind schemes on a bedrock-step exact solution. Then the method is applied to a real ice sheet by computing the steady-state shape of the Greenland ice sheet in a present-day modeled climate, at high resolution including sub-kilometer grids. An Appendix addresses the analytical calculation of the Jacobian in the
![]() ${M^{\rm \star}} $
scheme.
${M^{\rm \star}} $
scheme.
2. CONTINUUM MODEL
The time-dependent evolution equation for the ice thickness H is a statement of mass conservation:
Here q denotes the vertically integrated flux and m is the surface mass balance, also called the accumulation/ablation function. The SIA, the simplest relationship between H and q in common use in glaciology, is a lubrication approximation (Fowler, Reference Fowler1997) of the Stokes equations for ice in non-sliding contact with the bed. We only consider the isothermal, Glen's flow law (Greve and Blatter, Reference Greve and Blatter2009) case. Let b be the bed elevation and s = H + b the ice surface elevation. The flux q is given by
Here Γ = 2A(ρg) n /(n + 2) is a positive constant derived from the power n ≥ 1 and ice softness A in Glen's flow law, and from the ice density ρ and gravity g.
The flux q has several factored forms equivalent to Eqn (2). For instance, because it is common to combine Eqns (1) and (2) into a nonlinear diffusion equation (Huybrechts and others, Reference Huybrechts1996), one may write
Diffusion interpretation Eqn (3) is fully appropriate in the flat-bed case because Eqns (1) and (2) can be transformed to a p-Laplacian diffusion equation (Calvo and others, Reference Calvo, Díaz, Durany, Schiavi and Vázquez2002), but in general a diffusion interpretation is obscured by the bed gradient
![]() $\nabla b$
. If the bed is not flat then
$\nabla b$
. If the bed is not flat then
![]() $\nabla s$
and
$\nabla s$
and
![]() $\nabla H$
are different, so q is not strictly diffusive because it is not opposite to the gradient of the conserved quantity, namely H. For the same reason, non-flat beds are a barrier to proving well-posedness of the SIA (Jouvet and Bueler, Reference Jouvet and Bueler2012).
$\nabla H$
are different, so q is not strictly diffusive because it is not opposite to the gradient of the conserved quantity, namely H. For the same reason, non-flat beds are a barrier to proving well-posedness of the SIA (Jouvet and Bueler, Reference Jouvet and Bueler2012).
As an alternative to the diffusion form, one can compute a vertically averaged velocity V, and then treat the flux as arising from the transport of H by V:
In this case, Eqn (1) is apparently a hyperbolic conservation equation, but this appearance is also deceiving because the velocity depends in part on the gradient of the transported quantity.
Furthermore, non-zero
![]() $\nabla b$
generates numerical conservation errors at the ice margin. In addressing such errors, Jarosch and others (Reference Jarosch, Schoof and Anslow2013) propose a third form for the flux, namely
$\nabla b$
generates numerical conservation errors at the ice margin. In addressing such errors, Jarosch and others (Reference Jarosch, Schoof and Anslow2013) propose a third form for the flux, namely
The vector field ω can be thought of as a ‘velocity’ which transports H n+2. In this thinking the combination of Eqns (1) and (5) becomes a kind of nonlinear hyperbolic equation, but again ω depends on the gradient of the transported quantity H, so the combined equation is not truly hyperbolic.
We instead modify forms (3) and (5) to a split form
and where D is the same as in Eqn (3). The vector field W transports H
n+2, and is proportional to
![]() $\nabla b$
. Only the magnitude of W is influenced by
$\nabla b$
. Only the magnitude of W is influenced by
![]() $\nabla H$
. Note that
$\nabla H$
. Note that
![]() ${\bf W} = 0$
in the case of flat beds, while
ω
is non-zero and q is actually diffusive in that case.
${\bf W} = 0$
in the case of flat beds, while
ω
is non-zero and q is actually diffusive in that case.
The combination of Eqn (1) with any of the above flux forms (2–6) defines a highly nonlinear diffusion–advection equation. It is important to note that Eqns (2–6) all describe exactly the same flux, even though the different appearances have often influenced modelers' choices of numerical scheme details. Form (6) has the numerical advantage that we can apply a non-oscillatory transport scheme to
![]() ${\bf W}{H^{n + 2}}$
while also preserving accuracy by applying a centered scheme to
${\bf W}{H^{n + 2}}$
while also preserving accuracy by applying a centered scheme to
![]() $ - D\nabla H$
. Also, the often-dominant diffusion
$ - D\nabla H$
. Also, the often-dominant diffusion
![]() $ - D\nabla H$
is a strong motivation to use implicit time-stepping, while implicit steps are not a common approach for hyperbolic problems.
$ - D\nabla H$
is a strong motivation to use implicit time-stepping, while implicit steps are not a common approach for hyperbolic problems.
In this paper, we will primarily solve the steady-state form of Eqn (1), namely
By the divergence theorem, applied to any subregion V of Ω, we get the flux-integral form, equivalent to Eqn (7), namely
Here ∂V denotes the boundary of V, n is the outward normal unit vector, and ds is the length element on the closed curve ∂V. Our numerical schemes will be based on Eqn (8).
Equation (8) is solved as a boundary-value problem where both H = 0 and q = 0 apply along the (free) boundary. However, the location where those boundary conditions apply is unknown (Jouvet and Bueler, Reference Jouvet and Bueler2012; Jarosch and others, Reference Jarosch, Schoof and Anslow2013). The ice-covered domain where Eqn (8) applies cannot be treated as a small modification of a known domain, though that approach can be taken in explicit time-stepping schemes for Eqn (1) (Huybrechts and others, Reference Huybrechts1996; Bueler and others, Reference Bueler, Lingle, Kallen-Brown, Covey and Bowman2005).
To be more precise about the free-boundary conditions, the input data consist only of the bed elevation b(x, y) and the (steady) surface mass balance m(x, y). These input data must be defined on a larger, fixed computational domain Ω than the ice-covered set. If the surface mass balance m is sufficiently negative in the region near the boundary of Ω on which Eqn (8) is solved, then H → 0 at locations inside Ω, namely at the ice margin (free boundary). But also
![]() ${\bf q} \to 0$
at the same locations because ice does not flow past the margin. Because of the factor H
n+2 in Eqn (3) for the diffusivity D, the problem has degenerate diffusivity, that is, D → 0 at the free boundary. Solving Eqn (8), or computing a time step of Eqn (1), as such a free-boundary problem, without a boundary flux applied along any part of the (fixed) boundary of Ω, is usually called a ‘whole’ ice-sheet model. We restrict our attention to such whole ice-sheet models.
${\bf q} \to 0$
at the same locations because ice does not flow past the margin. Because of the factor H
n+2 in Eqn (3) for the diffusivity D, the problem has degenerate diffusivity, that is, D → 0 at the free boundary. Solving Eqn (8), or computing a time step of Eqn (1), as such a free-boundary problem, without a boundary flux applied along any part of the (fixed) boundary of Ω, is usually called a ‘whole’ ice-sheet model. We restrict our attention to such whole ice-sheet models.
In this paper, we solve coupled Eqns (6) and (8), with D computed as in Eqn (3). As noted above, we assume m is sufficiently negative in the region near the boundary of Ω, so that the ice-covered set is surrounded by ice-free areas. Any contact with the ocean must be modeled as strongly negative values of m, and there is no modeled floating ice. The solution is the non-negative thickness function H(x, y), defined everywhere in Ω and equal to zero where there is no ice.
3. METHODS
3.1. Classical Mahaffy scheme
Consider the rectangular structured FD grid, with spacing Δx, Δy, shown in Figure 1a. The Mahaffy (Reference Mahaffy1976) scheme, which is also ‘method 2’ in Hindmarsh and Payne (Reference Hindmarsh and Payne1996), calculates a flux component at each of the staggered grid points based on values at regular points (x j , y k ). For the staggered grid we introduce notation:

Fig. 1. (a) A structured FD grid with regular (dots) and staggered (triangles) points. (b) The same grid as an FVE grid with rectangular elements
![]() ${{\rm \squ} _{j,k}}$
(solid), nodes (dots), a dual rectangular control volume V
j,k
(dashed) and Mahaffy's flux-evaluation locations (circles). The corners of element
${{\rm \squ} _{j,k}}$
(solid), nodes (dots), a dual rectangular control volume V
j,k
(dashed) and Mahaffy's flux-evaluation locations (circles). The corners of element
![]() ${{\rm \squ} _{j,k}}$
are locally indexed by ℓ.
${{\rm \squ} _{j,k}}$
are locally indexed by ℓ.
At
![]() $(x_j^ + , {y_k})$
the scheme computes the x-component of the flux by
$(x_j^ + , {y_k})$
the scheme computes the x-component of the flux by
where s j,k = H j,k + b j,k ,
and ‘α
▸’ is an estimate of the slope
![]() $\vert \nabla s\vert $
at
$\vert \nabla s\vert $
at
![]() $(x_j^ + , {y_k})$
given by
$(x_j^ + , {y_k})$
given by
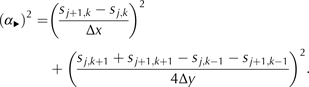 $$\eqalign{{({\alpha _{\blacktriangleright}} )^2} = & {\left( {\displaystyle{{{s_{\,j + 1,k}} - {s_{\,j,k}}} \over {\Delta x}}} \right)^2} \cr & + {\left( {\displaystyle{{{s_{\,j,k + 1}} + {s_{\,j + 1,k + 1}} - {s_{\,j,k - 1}} - {s_{\,j + 1,k - 1}}} \over {4\Delta y}}} \right)^2}.} $$
$$\eqalign{{({\alpha _{\blacktriangleright}} )^2} = & {\left( {\displaystyle{{{s_{\,j + 1,k}} - {s_{\,j,k}}} \over {\Delta x}}} \right)^2} \cr & + {\left( {\displaystyle{{{s_{\,j,k + 1}} + {s_{\,j + 1,k + 1}} - {s_{\,j,k - 1}} - {s_{\,j + 1,k - 1}}} \over {4\Delta y}}} \right)^2}.} $$
At
![]() $({x_j},y_k^ + )$
the scheme computes
$({x_j},y_k^ + )$
the scheme computes
where
![]() ${\hat H_{j,k + (1/2)}}$
and α
▸ are defined by swapping the roles of j and k, and Δx and Δy, in Eqns (11) and (12). The slope approximation in Eqn (12) is perhaps the least-obvious aspect of the Mahaffy scheme, but one may check that these FD formulas are consistent (Morton and Mayers, Reference Morton and Mayers2005) with Eqn (2).
${\hat H_{j,k + (1/2)}}$
and α
▸ are defined by swapping the roles of j and k, and Δx and Δy, in Eqns (11) and (12). The slope approximation in Eqn (12) is perhaps the least-obvious aspect of the Mahaffy scheme, but one may check that these FD formulas are consistent (Morton and Mayers, Reference Morton and Mayers2005) with Eqn (2).
The discretization of mass conservation, Eqn (7), uses straightforward centered differences (Morton and Mayers, Reference Morton and Mayers2005):
 $$\displaystyle{{q_{\,j + 1/2,k}^x - q_{\,j - 1/2,k}^x} \over {\Delta x}} + \displaystyle{{q_{\,j,k + 1/2}^y - q_{\,j,k - 1/2}^y} \over {\Delta y}} = {m_{\,j,k}},$$
$$\displaystyle{{q_{\,j + 1/2,k}^x - q_{\,j - 1/2,k}^x} \over {\Delta x}} + \displaystyle{{q_{\,j,k + 1/2}^y - q_{\,j,k - 1/2}^y} \over {\Delta y}} = {m_{\,j,k}},$$
where m j,k = m(x j , y k ). Equation (14) relates the nine unknown values of H at the regular grid points in Figure 1a, thus giving the ‘stencil’ of the scheme. It is required to hold at all regular grid points, thus forming a (generally) large, but finite, non-linear algebraic system.
3.2. FVE reinterpretation
The above description of the Mahaffy FD method is familiar to numerical ice-sheet modelers, but we now re-derive the scheme from an FVE perspective. Our reinterpretation uses the same structured grid, but the regular grid points are now nodes (degrees of freedom) for a continuous space of trial functions. Any FE method supposes that an approximation H
h
of the solution lies in some finite-dimensional space of functions that are sufficiently well-behaved so that the approximate flux
![]() ${{\bf q}^h}$
is defined almost everywhere. In an FV method, however, an integral equation like Eqn (8) is required to hold for a finite set of control volumes V which tile Ω (LeVeque, Reference LeVeque2002).
${{\bf q}^h}$
is defined almost everywhere. In an FV method, however, an integral equation like Eqn (8) is required to hold for a finite set of control volumes V which tile Ω (LeVeque, Reference LeVeque2002).
In Figure 1b, element
![]() ${{\rm \squ} _{j,k}}$
is the rectangle with lower-left corner at (x
j
, y
k
). When associated with bilinear functions this rectangle is a Q
1 FE (Elman and others, Reference Elman, Silvester and Wathen2005). A basis for bilinear functions on
${{\rm \squ} _{j,k}}$
is the rectangle with lower-left corner at (x
j
, y
k
). When associated with bilinear functions this rectangle is a Q
1 FE (Elman and others, Reference Elman, Silvester and Wathen2005). A basis for bilinear functions on
![]() ${{\rm \squ} _{j,k}}$
is the set
${{\rm \squ} _{j,k}}$
is the set
for ℓ = 0, 1, 2, 3, where
With this order, χ ℓ = 1 on element corners traversed in counterclockwise order (Fig. 1b).
Let S
h
be the trial space of functions that are continuous on the whole computational domain Ω and bilinear on each element
![]() ${{\rm \squ} _{j,k}}$
. Functions in S
h
have a bounded gradient that is defined almost everywhere, but the gradient is discontinuous along the element edges (solid lines in Fig. 1b). We write ψ
j,k
(x, y) for the unique function in S
h
so that ψ
j,k
(x
r
, y
s
) = δ
jr
δ
ks
(Fig. 2a); such functions form a basis of S
h
. We seek an approximate solution H
h
from S
h
. Also let b
h
in S
h
be the interpolant of the bed elevation data b, and let s
h
= H
h
+ b
h
. We denote by
${{\rm \squ} _{j,k}}$
. Functions in S
h
have a bounded gradient that is defined almost everywhere, but the gradient is discontinuous along the element edges (solid lines in Fig. 1b). We write ψ
j,k
(x, y) for the unique function in S
h
so that ψ
j,k
(x
r
, y
s
) = δ
jr
δ
ks
(Fig. 2a); such functions form a basis of S
h
. We seek an approximate solution H
h
from S
h
. Also let b
h
in S
h
be the interpolant of the bed elevation data b, and let s
h
= H
h
+ b
h
. We denote by
![]() ${{\bf q}^h}$
the flux computed from formula (6) using H
h
, b
h
and s
h
, so that
${{\bf q}^h}$
the flux computed from formula (6) using H
h
, b
h
and s
h
, so that
![]() ${{\bf q}^h}$
is well defined on the interior of each element.
${{\bf q}^h}$
is well defined on the interior of each element.

Fig. 2. (a) A continuous ‘hat’ basis function ψ
j,k
in the trial space S
h
. (b) A full FE interpretation of our scheme would use piecewise-constant basis functions ω
j,k
from the test space
![]() $S_h^* $
.
$S_h^* $
.
Let V j,k be the control volume with center at (x j , y k ) shown in Figure 1b. In the FVE method, we require Eqn (8) to hold for q = q h and V equal to each V j,k . Because we use a periodic grid with N x rectangles in the x-direction and N y in the y-direction, there are N = N x N y nodes, N distinct control volumes and N equations in the algebraic system.
Instead of control volumes, in a full FE interpretation we would introduce test functions. We can also do this for our scheme, as follows. Let
![]() $S_h^* $
be the space of functions that are constant on each control volume V
j,k
. These functions are piecewise-constant and discontinuous along the control volume edges. A basis of
$S_h^* $
be the space of functions that are constant on each control volume V
j,k
. These functions are piecewise-constant and discontinuous along the control volume edges. A basis of
![]() $S_h^* $
is formed by those functions which are one at a single node and zero at all other nodes; Figure 2b shows such a function ω
j,k
. Requiring Eqn (8) to hold for each control volume in our FVE method is equivalent to multiplying Eqn (7) by ω
j,k
and then integrating by parts. Showing the equivalence would require generalized functions, however, as the derivative of a step function is a Dirac delta function. Because we adopt the FVE interpretation, we have no further need for test functions, the space
$S_h^* $
is formed by those functions which are one at a single node and zero at all other nodes; Figure 2b shows such a function ω
j,k
. Requiring Eqn (8) to hold for each control volume in our FVE method is equivalent to multiplying Eqn (7) by ω
j,k
and then integrating by parts. Showing the equivalence would require generalized functions, however, as the derivative of a step function is a Dirac delta function. Because we adopt the FVE interpretation, we have no further need for test functions, the space
![]() $S_h^* $
or generalized functions.
$S_h^* $
or generalized functions.
Both this reinterpreted Mahaffy scheme, and our improved scheme below, assume midpoint quadrature on the right-hand integral in Eqn (8). Thus, we seek H h in S h satisfying
for all j, k.
However, it remains to do quadrature on the left in Eqn (16). We decompose the integral over the four edges of ∂V j,k :
 $$\eqalign{\int_{\partial {V_{\,j,k}}} {{\bf q}^h} \cdot {\bf n}\,{\rm d}s \,=\,\, & \int_{y_k^ -} ^{y_k^ +} {q^x}(x_j^ +, y)\,{\rm d}y \cr & + \int_{x_j^ -} ^{x_j^ +} {q^y}(x,y_k^ + )\,{\rm d}x \cr & - \int_{y_k^ -} ^{y_k^ +} {q^x}(x_j^ -, y)\,{\rm d}y \cr & - \int_{x_j^ -} ^{x_j^ +} {q^y}(x,y_k^ - )\,{\rm d}x.} $$
$$\eqalign{\int_{\partial {V_{\,j,k}}} {{\bf q}^h} \cdot {\bf n}\,{\rm d}s \,=\,\, & \int_{y_k^ -} ^{y_k^ +} {q^x}(x_j^ +, y)\,{\rm d}y \cr & + \int_{x_j^ -} ^{x_j^ +} {q^y}(x,y_k^ + )\,{\rm d}x \cr & - \int_{y_k^ -} ^{y_k^ +} {q^x}(x_j^ -, y)\,{\rm d}y \cr & - \int_{x_j^ -} ^{x_j^ +} {q^y}(x,y_k^ - )\,{\rm d}x.} $$
The flux
![]() ${{\bf q}^h}$
is a bounded function, but it is discontinuous across element boundaries. In the first right-hand integral in Eqn (17), the integrand has a jump discontinuity at the midpoint of the interval of integration (i.e. at y = y
k
; note
${{\bf q}^h}$
is a bounded function, but it is discontinuous across element boundaries. In the first right-hand integral in Eqn (17), the integrand has a jump discontinuity at the midpoint of the interval of integration (i.e. at y = y
k
; note
![]() $\partial {s^h}/\partial y = s_y^h $
is discontinuous there), but formula (10) in the Mahaffy FD scheme computes the normal component of
$\partial {s^h}/\partial y = s_y^h $
is discontinuous there), but formula (10) in the Mahaffy FD scheme computes the normal component of
![]() ${{\bf q}^h}$
exactly at that midpoint.
${{\bf q}^h}$
exactly at that midpoint.
The key to reinterpreting the Mahaffy scheme is that it computes each integral in Eqn (17) by the midpoint method using averages of the discontinuous surface gradient across its jump discontinuities. The scheme does not use true quadrature because the integrand
![]() ${{\bf q}^h} \cdot {\bf n}$
does not have a value at the quadrature point. To turn this idea into formulas, first observe that both the thickness H
h
and the x-derivative
${{\bf q}^h} \cdot {\bf n}$
does not have a value at the quadrature point. To turn this idea into formulas, first observe that both the thickness H
h
and the x-derivative
![]() $\partial {s^h}/\partial x = s_x^h $
are continuous along the edge between elements
$\partial {s^h}/\partial x = s_x^h $
are continuous along the edge between elements
![]() ${{\rm \squ} _{j,k}}$
and
${{\rm \squ} _{j,k}}$
and
![]() ${{\rm \squ} _{j,k - 1}}$
. In fact, using element basis (15), the surface gradient on
${{\rm \squ} _{j,k - 1}}$
. In fact, using element basis (15), the surface gradient on
![]() ${{\rm \squ} _{j,k}}$
has components
${{\rm \squ} _{j,k}}$
has components
 $$\eqalign{s_x^h (x,y) =\, & \displaystyle{{{s_{\,j + 1,k}} - {s_{\,j,k}}} \over {\Delta x}}\left( {1 - \displaystyle{{y - {y_k}} \over {\Delta y}}} \right) \cr & + \displaystyle{{{s_{\,j + 1,k + 1}} - {s_{\,j,k + 1}}} \over {\Delta x}}\left( {\displaystyle{{y - {y_k}} \over {\Delta y}}} \right), \cr s_y^h (x,y) =\, & \displaystyle{{{s_{\,j,k + 1}} - {s_{\,j,k}}} \over {\Delta y}}\left( {1 - \displaystyle{{x - {x_j}} \over {\Delta x}}} \right) \cr & + \displaystyle{{{s_{\,j + 1,k + 1}} - {s_{\,j + 1,k}}} \over {\Delta y}}\left( {\displaystyle{{x - {x_j}} \over {\Delta x}}} \right).} $$
$$\eqalign{s_x^h (x,y) =\, & \displaystyle{{{s_{\,j + 1,k}} - {s_{\,j,k}}} \over {\Delta x}}\left( {1 - \displaystyle{{y - {y_k}} \over {\Delta y}}} \right) \cr & + \displaystyle{{{s_{\,j + 1,k + 1}} - {s_{\,j,k + 1}}} \over {\Delta x}}\left( {\displaystyle{{y - {y_k}} \over {\Delta y}}} \right), \cr s_y^h (x,y) =\, & \displaystyle{{{s_{\,j,k + 1}} - {s_{\,j,k}}} \over {\Delta y}}\left( {1 - \displaystyle{{x - {x_j}} \over {\Delta x}}} \right) \cr & + \displaystyle{{{s_{\,j + 1,k + 1}} - {s_{\,j + 1,k}}} \over {\Delta y}}\left( {\displaystyle{{x - {x_j}} \over {\Delta x}}} \right).} $$
On
![]() ${{\rm \squ} _{j,k - 1}}$
,
${{\rm \squ} _{j,k - 1}}$
,
![]() $s_x^h $
and
$s_x^h $
and
![]() $s_y^h $
can be calculated by shifting the index k to k − 1. Thus, the continuous function
$s_y^h $
can be calculated by shifting the index k to k − 1. Thus, the continuous function
![]() $s_x^h $
has value
$s_x^h $
has value
at the midpoint in the first integral in Eqn (17). Similarly, writing out H h using element basis (15) gives
at the midpoint, which is Eqn (11). The y-derivative
![]() $s_y^h $
, however, has different values above (on
$s_y^h $
, however, has different values above (on
![]() ${{\rm \squ} _{j,k}}$
) and below (on
${{\rm \squ} _{j,k}}$
) and below (on
![]() ${{\rm \squ} _{j,k - 1}}$
) the element boundary at y = y
k
. The limits are:
${{\rm \squ} _{j,k - 1}}$
) the element boundary at y = y
k
. The limits are:
 $$\eqalign{\mathop {\lim} \limits_{y \to y_k^ +} s_y^h (x_j^ +, y) & =\, \displaystyle{{{s_{\,j,k + 1}} - {s_{\,j,k}} + {s_{\,j + 1,k + 1}} - {s_{\,j + 1,k}}} \over {2\Delta y}}, \cr \mathop {\lim} \limits_{y \to y_k^ -} s_y^h (x_j^ +, y) & =\, \displaystyle{{{s_{\,j,k}} - {s_{\,j,k - 1}} + {s_{\,j + 1,k}} - {s_{\,j + 1,k - 1}}} \over {2\Delta y}}.} $$
$$\eqalign{\mathop {\lim} \limits_{y \to y_k^ +} s_y^h (x_j^ +, y) & =\, \displaystyle{{{s_{\,j,k + 1}} - {s_{\,j,k}} + {s_{\,j + 1,k + 1}} - {s_{\,j + 1,k}}} \over {2\Delta y}}, \cr \mathop {\lim} \limits_{y \to y_k^ -} s_y^h (x_j^ +, y) & =\, \displaystyle{{{s_{\,j,k}} - {s_{\,j,k - 1}} + {s_{\,j + 1,k}} - {s_{\,j + 1,k - 1}}} \over {2\Delta y}}.} $$
The average of these values is not a value of
![]() $s_y^h $
, but a reconstruction:
$s_y^h $
, but a reconstruction:
Formula (22) is exactly the estimate of ∂s/∂y which appears in FD formula (12).
In our FVE reinterpretation, the Mahaffy FD scheme uses Eqns (19), (20) and (22) in the midpoint rule for the first integral in Eqn (17):
 $$\eqalign{ & \int_{y_k^ -} ^{y_k^ +} {q^x}(x_j^ +, y)\,{\rm d}y \cr & \quad \approx - \Delta y\Gamma {({H^h}(x_j^ +, {y_k}))^{n + 2}}{({\alpha _{\blacktriangleright}} )^{n - 1}}s_x^h (x_j^ +, {y_k}),} $$
$$\eqalign{ & \int_{y_k^ -} ^{y_k^ +} {q^x}(x_j^ +, y)\,{\rm d}y \cr & \quad \approx - \Delta y\Gamma {({H^h}(x_j^ +, {y_k}))^{n + 2}}{({\alpha _{\blacktriangleright}} )^{n - 1}}s_x^h (x_j^ +, {y_k}),} $$
where
is the same as in Eqn (12). Thus, the FD scheme approximates each integral on the right in Eqn (17) by a perfectly reasonable quadrature ‘crime’ (cf. Strang, Reference Strang1972) which averages across a discontinuity to reconstruct a slope. Recognizing the Mahaffy choice as quadrature-like, in this FVE context, is beneficial because it allows us to improve the scheme.
3.3. Improved quadrature
If the goal is to accurately generate an algebraic equation from Eqn (16) by quadrature along ∂V
j,k
, then it is easy to improve the quadrature. We also use flux decomposition Eqn (6) with an upwind-type discretization on the bed gradient term
![]() ${\bf W}{H^{n + 2}}$
(Section 3.4). Together these improvements define our new ‘
${\bf W}{H^{n + 2}}$
(Section 3.4). Together these improvements define our new ‘
![]() ${M^{\rm \star}} $
’ scheme.
${M^{\rm \star}} $
’ scheme.
As already noted, the numerical approximation
![]() ${{\bf q}^h}$
from Eqn (6) is defined and smooth on the interior of each element, but discontinuous across element boundaries. So we break each interval of integration on the right-hand side of Eqn (17) into two parts and use the midpoint rule, the optimal one-point rule, on each half. For example, we break the first integral at y = y
k
:
${{\bf q}^h}$
from Eqn (6) is defined and smooth on the interior of each element, but discontinuous across element boundaries. So we break each interval of integration on the right-hand side of Eqn (17) into two parts and use the midpoint rule, the optimal one-point rule, on each half. For example, we break the first integral at y = y
k
:
 $$\eqalign{ & \int_{y_k^ -} ^{y_k^ +} {q^x}(x_j^ +, y)\,{\rm d}y \cr & \quad = \int_{y_k^ -} ^{{y_k}} {q^x}(x_j^ +, y)\;{\rm d}y + \int_{{y_k}}^{y_k^ +} {q^x}(x_j^ +, y)\,{\rm d}y \cr & \quad = \displaystyle{{\Delta y} \over 2}\left( {{q^x}(x_j^ +, {y_k} - {\textstyle{{\Delta y} \over 4}}) + {q^x}(x_j^ +, {y_k} + {\textstyle{{\Delta y} \over 4}})} \right).} $$
$$\eqalign{ & \int_{y_k^ -} ^{y_k^ +} {q^x}(x_j^ +, y)\,{\rm d}y \cr & \quad = \int_{y_k^ -} ^{{y_k}} {q^x}(x_j^ +, y)\;{\rm d}y + \int_{{y_k}}^{y_k^ +} {q^x}(x_j^ +, y)\,{\rm d}y \cr & \quad = \displaystyle{{\Delta y} \over 2}\left( {{q^x}(x_j^ +, {y_k} - {\textstyle{{\Delta y} \over 4}}) + {q^x}(x_j^ +, {y_k} + {\textstyle{{\Delta y} \over 4}})} \right).} $$
Recalling notation (9), values
![]() ${q^x}(x_j^ + , {y_k} \pm (\Delta y/4))$
are evaluations of
${q^x}(x_j^ + , {y_k} \pm (\Delta y/4))$
are evaluations of
![]() ${{\bf q}^h}$
at points of continuity.
${{\bf q}^h}$
at points of continuity.
Similar formulas apply to the other three integrals on the right-hand side of Eqn (17). Figure 3 shows all eight quadrature points needed to compute the full integral over ∂V
j,k
in Eqn (16). At each point we evaluate the x- or y-component of
![]() ${{\bf q}^h}$
and multiply by a constant to get the appropriate integral. Thus, our approximation of Eqn (16) is
${{\bf q}^h}$
and multiply by a constant to get the appropriate integral. Thus, our approximation of Eqn (16) is
 $$\sum\limits_{s = 0}^7\,{{\bf c}_s} \cdot {{\bf q}^h}(x_j^s, y_k^s ) = {m_{\,j,k}}{\kern 1pt} \Delta x{\kern 1pt} \Delta y,$$
$$\sum\limits_{s = 0}^7\,{{\bf c}_s} \cdot {{\bf q}^h}(x_j^s, y_k^s ) = {m_{\,j,k}}{\kern 1pt} \Delta x{\kern 1pt} \Delta y,$$
where
 $$\eqalign{& {{\bf c}_0} = {{\bf c}_7} = \left( {0,\;\displaystyle{{\Delta y} \over 2}} \right), \cr & {{\bf c}_1} = {{\bf c}_2} = \left( {\displaystyle{{\Delta x} \over 2},\;0} \right), \cr & {{\bf c}_3} = {{\bf c}_4} = \left( {0,\; - \displaystyle{{\Delta y} \over 2}} \right), \cr & {{\bf c}_5} = {{\bf c}_6} = \left( { - \displaystyle{{\Delta x} \over 2},\;0} \right),} $$
$$\eqalign{& {{\bf c}_0} = {{\bf c}_7} = \left( {0,\;\displaystyle{{\Delta y} \over 2}} \right), \cr & {{\bf c}_1} = {{\bf c}_2} = \left( {\displaystyle{{\Delta x} \over 2},\;0} \right), \cr & {{\bf c}_3} = {{\bf c}_4} = \left( {0,\; - \displaystyle{{\Delta y} \over 2}} \right), \cr & {{\bf c}_5} = {{\bf c}_6} = \left( { - \displaystyle{{\Delta x} \over 2},\;0} \right),} $$
and
 $$\eqalign{& x_j^0 = x_j^7 = {x_j} + \displaystyle{{\Delta x} \over 2},\quad y_k^1 = y_k^2 = {y_k} + \displaystyle{{\Delta y} \over 2}, \cr & x_j^1 = x_j^6 = {x_j} + \displaystyle{{\Delta x} \over 4},\quad y_k^0 = y_k^3 = {y_k} + \displaystyle{{\Delta y} \over 4}, \cr & x_j^2 = x_j^5 = {x_j} - \displaystyle{{\Delta x} \over 4},\quad y_k^4 = y_k^7 = {y_k} - \displaystyle{{\Delta y} \over 4}, \cr & x_j^3 = x_j^4 = {x_j} - \displaystyle{{\Delta x} \over 2},\quad y_k^5 = y_k^6 = {y_k} - \displaystyle{{\Delta y} \over 2}.} $$
$$\eqalign{& x_j^0 = x_j^7 = {x_j} + \displaystyle{{\Delta x} \over 2},\quad y_k^1 = y_k^2 = {y_k} + \displaystyle{{\Delta y} \over 2}, \cr & x_j^1 = x_j^6 = {x_j} + \displaystyle{{\Delta x} \over 4},\quad y_k^0 = y_k^3 = {y_k} + \displaystyle{{\Delta y} \over 4}, \cr & x_j^2 = x_j^5 = {x_j} - \displaystyle{{\Delta x} \over 4},\quad y_k^4 = y_k^7 = {y_k} - \displaystyle{{\Delta y} \over 4}, \cr & x_j^3 = x_j^4 = {x_j} - \displaystyle{{\Delta x} \over 2},\quad y_k^5 = y_k^6 = {y_k} - \displaystyle{{\Delta y} \over 2}.} $$

Fig. 3. For Eqn (26) we evaluate
![]() ${{\bf q}^h}(x,y)$
at eight quadrature points (numbered circles) along ∂V
j,k
(dashed).
${{\bf q}^h}(x,y)$
at eight quadrature points (numbered circles) along ∂V
j,k
(dashed).
Implementing Eqn (26) therefore requires evaluating
![]() ${{\bf q}^h}$
at eight quadrature points, twice the number for the classical method, but the stencils are the same because we use the same nine nodal values of H
h
.
${{\bf q}^h}$
at eight quadrature points, twice the number for the classical method, but the stencils are the same because we use the same nine nodal values of H
h
.
One could propose further-improved quadrature, replacing the midpoint rule by higher-order methods like two-point Gauss–Legendre. Also, our Q
1 elements could be replaced by higher-order (e.g. Q
2) elements. Though such methods have not been tested, in fact the largest numerical SIA errors occur near the ice margin where the solution H has unbounded gradient (Bueler and others, Reference Bueler, Lingle, Kallen-Brown, Covey and Bowman2005). Thus, higher-order quadrature and interpolation will not give much advantage. We believe our improved method represents a measurable accuracy and Newton-iteration-convergence improvement over the classical Mahaffy method (Section 4) because it evaluates
![]() ${{\bf q}^h}$
at points of continuity, not because the order of quadrature or interpolation is flawed in the classical scheme.
${{\bf q}^h}$
at points of continuity, not because the order of quadrature or interpolation is flawed in the classical scheme.
3.4. Improvement from upwinding
Jarosch and others (Reference Jarosch, Schoof and Anslow2013) show that the Mahaffy scheme can suffer from significant mass-conservation errors at locations of abrupt change in the bed elevation. In such cases where the bed gradient dominates the flux, the mass-conservation equation has more ‘hyperbolic’ character. Thus, Jarosch and others use a high-resolution upwind scheme (LeVeque, Reference LeVeque2002) based on flux form Eqn (5). They show reduced mass-conservation errors in the sense of giving numerical solutions that are closer in volume to an exact solution. On the other hand, their scheme, which solves the time-dependent Eqn (1) using explicit time-stepping, expands the stencil because it needs values two grid spaces away.
By comparison, we propose using minimal first-order upwinding based on form (6) of the flux, even though upwinding is not required for either linear stability or non-oscillation of our implicit scheme (Morton and Mayers, Reference Morton and Mayers2005). Numerical testing suggests upwinding is effective in our case because it improves the conditioning of the Jacobian matrix used in the Newton iteration (not shown).
In our improved scheme, the transport-type flux
![]() $\tilde {\bf {q}}= {{\bf W}}{H^{n + 2}}$
uses H evaluated at a location different from the quadrature point, according to the direction of W evaluated at the quadrature point. For instance, our upwind modification at
$\tilde {\bf {q}}= {{\bf W}}{H^{n + 2}}$
uses H evaluated at a location different from the quadrature point, according to the direction of W evaluated at the quadrature point. For instance, our upwind modification at
![]() $(x_j^0, y_k^0 )$
– see Figure 3 – uses the sign of
$(x_j^0, y_k^0 )$
– see Figure 3 – uses the sign of
where
![]() ${{\bf W}} = ({W^x},\;{W^y})$
. Note that the sign of
${{\bf W}} = ({W^x},\;{W^y})$
. Note that the sign of
![]() $W_*^x $
is opposite that of the x-component of
$W_*^x $
is opposite that of the x-component of
![]() $\nabla {b^h}$
at
$\nabla {b^h}$
at
![]() $(x_j^0, y_k^0 )$
. We shift the evaluation of H upwind by a fraction 0 ≤ λ ≤ 1 of an element width,
$(x_j^0, y_k^0 )$
. We shift the evaluation of H upwind by a fraction 0 ≤ λ ≤ 1 of an element width,
 $$\eqalign{ & {\tilde {\bf {q}}^x}(x_j^0 ,\;y_k^0 ) \cr & \quad = W_{\ast }^x \left\{ {\matrix{ {H{{(x_j^0 - \lambda {\textstyle{{\Delta x} \over 2}},\;y_k^0 )}^{n + 2}},} & {W_{\ast }^x \ge 0,} \cr {H{{(x_j^0 + \lambda {\textstyle{{\Delta x} \over 2}},\;y_k^0 )}^{n + 2}},} & {W_{\ast }^x \lt 0,} \cr } } \right.} $$
$$\eqalign{ & {\tilde {\bf {q}}^x}(x_j^0 ,\;y_k^0 ) \cr & \quad = W_{\ast }^x \left\{ {\matrix{ {H{{(x_j^0 - \lambda {\textstyle{{\Delta x} \over 2}},\;y_k^0 )}^{n + 2}},} & {W_{\ast }^x \ge 0,} \cr {H{{(x_j^0 + \lambda {\textstyle{{\Delta x} \over 2}},\;y_k^0 )}^{n + 2}},} & {W_{\ast }^x \lt 0,} \cr } } \right.} $$
where λ = 0 is no upwinding and λ = 1 is the maximum upwinding that does not expand the stencil. After experimentation (Section 4) we have chosen λ = 1/4 (Fig. 4). This value is seen to be large enough to improve the convergence of the Newton iteration but also small enough to generate substantial improvements in accuracy for the bedrock-step exact solution. Upwinding at the other seven points along ∂V j,k (Fig. 3) uses similar formulas.

Fig. 4. On element
![]() ${{\rm \squ} _{j,k}}$
, when computing the flux at quadrature points (circles), upwinding of the flux term
${{\rm \squ} _{j,k}}$
, when computing the flux at quadrature points (circles), upwinding of the flux term
![]() $$\tilde {\bf {q}} = {{\bf W}}{H^{n + 2}}$
evaluates the thicknesses H at locations shown with ‘+’, one-quarter of the way to the element boundary.
$$\tilde {\bf {q}} = {{\bf W}}{H^{n + 2}}$
evaluates the thicknesses H at locations shown with ‘+’, one-quarter of the way to the element boundary.
The ‘
![]() ${M^{\rm \star}} $
’ scheme combines both of the above improvements. We will see in verification (Section 4) that it achieves higher solution accuracy than either the apparently second-order Mahaffy scheme or the higher-resolution explicit advection scheme of Jarosch and others (Reference Jarosch, Schoof and Anslow2013). (Note that the additional non-smoothness of such high-resolution flux-limiting methods suggests caution when using a Newton scheme, which needs a differentiable residual function.) Convergence of the Newton iteration is also improved compared with the classical Mahaffy scheme. Evidence from both verification and realistic (Section 4) cases suggests that our form of upwinding is most important at locations of low regularity of the solution.
${M^{\rm \star}} $
’ scheme combines both of the above improvements. We will see in verification (Section 4) that it achieves higher solution accuracy than either the apparently second-order Mahaffy scheme or the higher-resolution explicit advection scheme of Jarosch and others (Reference Jarosch, Schoof and Anslow2013). (Note that the additional non-smoothness of such high-resolution flux-limiting methods suggests caution when using a Newton scheme, which needs a differentiable residual function.) Convergence of the Newton iteration is also improved compared with the classical Mahaffy scheme. Evidence from both verification and realistic (Section 4) cases suggests that our form of upwinding is most important at locations of low regularity of the solution.
3.5. Solution of the equations
It remains to describe the numerical solution of the system of highly nonlinear algebraic equations that is generated by the formulas above. This is additionally non-trivial because an inequality constraint applies to each unknown.
Each equation from the
![]() ${M^{\rm \ast}} $
scheme is Eqn (26) with an upwind modification like (30) at the quadrature points. The resulting system of N = N
x
N
y
equations is
${M^{\rm \ast}} $
scheme is Eqn (26) with an upwind modification like (30) at the quadrature points. The resulting system of N = N
x
N
y
equations is
This determines N unknowns, a vector
![]() ${{\bf H}} = \{ {H_{j,k}}\} $
; note H
h
(x, y) and H are actually two representations of the same discrete thickness approximation. System (31) is not adequate by itself, however, because each unknown thickness H
j,k
must be non-negative, that is,
${{\bf H}} = \{ {H_{j,k}}\} $
; note H
h
(x, y) and H are actually two representations of the same discrete thickness approximation. System (31) is not adequate by itself, however, because each unknown thickness H
j,k
must be non-negative, that is,
![]() ${{\bf H}} \ge 0$
.
${{\bf H}} \ge 0$
.
These requirements can be combined into a variational inequality (Kinderlehrer and Stampacchia, Reference Kinderlehrer and Stampacchia1980; Jouvet and Bueler, Reference Jouvet and Bueler2012). Equivalently, we can write them in nonlinear complementarity problem form (Benson and Munson, Reference Benson and Munson2006):
In fact, we will solve (32) by a ‘constrained’ Newton solver, specifically either by the reduced-space ( RS ) or semi-smooth ( SS ) methods (Benson and Munson, Reference Benson and Munson2006) implemented in PETSc (Balay and others, Reference Balay2015). Our open-source C code contains the residual and Jacobian evaluation subroutines. (To get the code and examples, clone the repository at https://github.com/bueler/sia-fve. Then see README.md in directory petsc/.) However, the parallel grid management, Newton solver, iterative linear solver and linear preconditioning methods are all inside the PETSc library, and they are chosen at runtime. Both multigrid (Briggs and others, Reference Briggs, Henson and McCormick2000) and additive-Schwarz-type domain decomposition (Smith and others, Reference Smith, Bjorstad and Gropp1996) preconditioning are found to work (not shown), but the latter is more robust and is used in all runs in Section 4.
The Jacobian of system (31), that is, the N × N matrix,
can be computed via hand-calculated derivatives. This additional effort (Appendix) gives a speed-up only by a factor of ~1.5 over the alternative, namely FD computation of Jacobian entries coming from additional residual (i.e. F) evaluations. Such approximate Jacobians are efficiently implemented in PETSc using ‘coloring’ of the nodes (Curtis and others, Reference Curtis, Powell and Reid1974) so that, because of the nine-point stencil, only a total of ten residual evaluations are needed to approximate J.
In the standard theory of Newton's method, quadratic convergence should occur if J is Lipschitz-continuous as a function of the unknowns (Kelley, Reference Kelley2003). However, the flux q here is generally not that smooth as a function of
![]() $\nabla H$
. In particular, for 1 < n < 3 the flux has a second derivative which is not Lipschitz-continuous with respect to changes in
$\nabla H$
. In particular, for 1 < n < 3 the flux has a second derivative which is not Lipschitz-continuous with respect to changes in
![]() $\nabla H$
. Because Eqn (26) already involves differentiating q, in the limit where the control volume shrinks to zero, the behavior of second derivatives of q determines the smoothness of J and thus the convergence of the solver. Non-smoothness is best seen in 1-D where Eqn (2) is
$\nabla H$
. Because Eqn (26) already involves differentiating q, in the limit where the control volume shrinks to zero, the behavior of second derivatives of q determines the smoothness of J and thus the convergence of the solver. Non-smoothness is best seen in 1-D where Eqn (2) is
when n >1,
for C > 0. If n = 2, for example, this function undergoes a step at H′ = −b′, and thus is not Lipschitz. In fact, Eqn (35) is not Lipschitz-continuous for 1 < n < 3.
Because we want methods that work for all exponents n ≥ 1, we regularize by replacing
with δ = 10−4, in computing q and its derivatives. This regularization, which makes little difference when the surface slope is of order 10−3 or larger, is similar to that used in regularizing the viscosity in the Stokes equations (Greve and Blatter, Reference Greve and Blatter2009) and other stress balance models (e.g. Bueler and Brown, Reference Bueler and Brown2009; Brown and others, Reference Brown, Smith and Ahmadia2013).
A Newton solver requires an initial iterate, and we generate it in two stages. First we apply a heuristic that seems to work adequately for both ice sheet- and glacier-scale problems, and is used by Jouvet and Gräser (Reference Jouvet and Gräser2013) in a time-stepping context. From the mass-balance data m j,k (m a−1) we compute
which builds the initial thickness simply by piling up 1000 years of accumulation.
In the second stage, we apply a simple ‘parameter continuation’ scheme, to aid in the convergence of the Newton iteration on our degenerate, non-linear free-boundary problem. We first apply the Newton method to an easier free-boundary problem, one with constant diffusivity. Then we adjust a continuation parameter ε until we solve the full SIA free-boundary problem. Specifically, for 0 ≤ ε ≤ 1 we define
where n is the original exponent, D is computed in Eqn (3), n 0 = 1, and D 0 is a typical scale of diffusivities for the problem (e.g. D 0 = 0.01 m2 s−1 for a glacier problem or D 0 = 10 m2 s−1 for an ice sheet). Note n(1) = n 0 and D(1) = D 0, while n(0) = n and D(0) = D. We consecutively solve free-boundary problems corresponding to 13 values of ε:
At the last stage ε12 = 0, the problem is the unmodified SIA. Note the parameter ε i is reduced by an order of magnitude as i increases by 3.
We start with ε0 = 1, so we are solving (32) with values n = n 0 and D = D 0 and initial iterate H (0) from (37). Once this first stage converges, the ice margin has moved far from the equilibrium line – which is the margin of initial iterate (37) – into the ablation zone as expected. The solution is then used as the initial iterate for problem (32) with the second value ε1 = (0.1)1/3 ≈ 0.46 in Eqn (38). Continuing in this way we eventually solve the unregularized n(0) = n and D(0) = D problem.
3.6. Time-stepping
The relationship between our steady-state computations and fully implicit time-stepping methods for Eqn (1) deserves examination. We will be able to exploit such time steps to make the Newton solver for the steady-state problem more robust for rough-bed cases.
The backward-Euler (Morton and Mayers, Reference Morton and Mayers2005) approximation of Eqn (1) is
where H
ℓ(x, y) ≈ H(t
ℓ, x, y) is the unknown thickness, H
ℓ−1 is known from the previous time step, and
![]() ${{{\bf q}}^\ell} $
is the flux computed using H
ℓ. Our methods extend easily from solving Eqn (32) to solving Eqn (40), subject, as before, to the constraint H
ℓ ≥ 0.
${{{\bf q}}^\ell} $
is the flux computed using H
ℓ. Our methods extend easily from solving Eqn (32) to solving Eqn (40), subject, as before, to the constraint H
ℓ ≥ 0.
Solving for steady state effectively requires taking infinite-duration implicit time steps in Eqn (40). Using finite Δt is easier than the steady-state problem, however, both because the initial iterate can be taken to be the solution at the previous time step, and because the continuation sequence can either be avoided entirely or truncated to only include small ε values. Even more important is the key fact that solving Eqn (40) gets easier as Δt → 0, because the Jacobian J has a dominanting diagonal contribution from the H ℓ/Δt term.
If a Newton iteration fails to converge in the steady-state case, we might hope that it would still converge for Eqn (40) using finite Δt, and this is what we see in practice. In fact, switching from the steady-state problem to long (e.g. 0.1–100 years depending on resolution) backward-Euler time steps is a ‘recovery strategy’ to cope with Newton solver difficulties when dealing with highly irregular bed topography data in the steady-state problem (Section 4).
4. RESULTS
We first apply our
![]() ${M^{\rm \ast}} $
method in two examples where exact solutions are known. We use the exact solutions to evaluate the convergence of the discrete solution to the continuum solution under grid refinement (verification), and we evaluate the convergence of the continuation scheme and Newton iteration in these cases. After that we apply the method to high-resolution Greenland ice-sheet bedrock topography. All computations in this section use physical parameters from European ice-sheet Modelling Initiative I (EISMINT I) (Huybrechts and others, Reference Huybrechts1996) and are in two horizontal variables, though we show some results along flowlines for clarity.
${M^{\rm \ast}} $
method in two examples where exact solutions are known. We use the exact solutions to evaluate the convergence of the discrete solution to the continuum solution under grid refinement (verification), and we evaluate the convergence of the continuation scheme and Newton iteration in these cases. After that we apply the method to high-resolution Greenland ice-sheet bedrock topography. All computations in this section use physical parameters from European ice-sheet Modelling Initiative I (EISMINT I) (Huybrechts and others, Reference Huybrechts1996) and are in two horizontal variables, though we show some results along flowlines for clarity.
4.1. Verification cases
An angularly symmetric steady-state exact solution exists in the flat-bed case (Bueler, Reference Bueler2003; van der Veen, Reference van der Veen2013). This ‘dome’ exact solution, with parameters suitable for a medium-sized ice sheet, is shown in Figure 5. The numerical results from our
![]() ${M^{\rm \star}} $
method are very close to the exact solution, with numerical error at the last positive-thickness grid point barely visible.
${M^{\rm \star}} $
method are very close to the exact solution, with numerical error at the last positive-thickness grid point barely visible.

Fig. 5. Result from
![]() ${M^{\rm \star}} $
method on a Δx = Δy = 25 km grid (dots) compared with the dome exact solution. The detail of the margin adds results from a 12.5 km grid (diamonds).
${M^{\rm \star}} $
method on a Δx = Δy = 25 km grid (dots) compared with the dome exact solution. The detail of the margin adds results from a 12.5 km grid (diamonds).
However, because of unbounded gradient at the margin, thickness errors decay slowly under grid refinement (Bueler and others, Reference Bueler, Lingle, Kallen-Brown, Covey and Bowman2005). Thus, we measure the maximum and average thickness errors from both classical Mahaffy and
![]() ${M^{\rm \star}} $
methods in Figure 6. Both methods show expected slow convergence of maximum error. The decay of the average error for
${M^{\rm \star}} $
methods in Figure 6. Both methods show expected slow convergence of maximum error. The decay of the average error for
![]() ${M^{\rm \star}} $
, to ~1 m for the three finest grids, is better than for classical Mahaffy. However, because of unbounded gradient at the margin, the measured
${M^{\rm \star}} $
, to ~1 m for the three finest grids, is better than for classical Mahaffy. However, because of unbounded gradient at the margin, the measured
![]() ${M^{\rm \star}} $
decay rate of O(Δx
1.47) is less good than the theoretical O(Δx
2) convergence rate expected from truncation-error analysis.
${M^{\rm \star}} $
decay rate of O(Δx
1.47) is less good than the theoretical O(Δx
2) convergence rate expected from truncation-error analysis.

Fig. 6. Average and maximum error under grid refinement using the dome exact solution, for the
![]() ${M^{\rm \star}} $
(stars) and classical Mahaffy (squares) methods. Gray circles indicate runs where the Newton method diverged before the last ε12 = 0 continuation stage.
${M^{\rm \star}} $
(stars) and classical Mahaffy (squares) methods. Gray circles indicate runs where the Newton method diverged before the last ε12 = 0 continuation stage.
Improved convergence of the Newton iteration for the
![]() ${M^{\rm \star}} $
scheme, which in this flat-bed case differs from the classical scheme only by improved quadrature, is seen in all cases. As indicated in Figure 6 by gray circles, Newton iteration for the classical Mahaffy scheme fails to converge for all grids except the coarsest. Though the
${M^{\rm \star}} $
scheme, which in this flat-bed case differs from the classical scheme only by improved quadrature, is seen in all cases. As indicated in Figure 6 by gray circles, Newton iteration for the classical Mahaffy scheme fails to converge for all grids except the coarsest. Though the
![]() ${M^{\rm \star}} $
Newton iteration fails to converge at the ε12 = 0 stage on the two finest grids, these cases fully converge if the problem is changed to a backward Euler step (Eqn (40)) of duration 100.0 years (not shown). Figure 7 shows clear evidence of quadratic, or at least superlinear, convergence from the Newton solver, in runs where the relative tolerance (i.e. residual 2-norm reduction factor) is set to 10−10. That is, at each stage ε
i
of the continuation scheme, the computed residual shows the characteristic curved drop of quadratic convergence on such semi-log axes (Kelley, Reference Kelley2003).
${M^{\rm \star}} $
Newton iteration fails to converge at the ε12 = 0 stage on the two finest grids, these cases fully converge if the problem is changed to a backward Euler step (Eqn (40)) of duration 100.0 years (not shown). Figure 7 shows clear evidence of quadratic, or at least superlinear, convergence from the Newton solver, in runs where the relative tolerance (i.e. residual 2-norm reduction factor) is set to 10−10. That is, at each stage ε
i
of the continuation scheme, the computed residual shows the characteristic curved drop of quadratic convergence on such semi-log axes (Kelley, Reference Kelley2003).

Fig. 7. Residual norm vs iteration number for each continuation stage. The SIA problem itself is the last ε12 = 0 curve.
To test performance on non-flat and non-smooth beds, we use a glacier-scale bedrock-step exact solution by Jarosch and others (Reference Jarosch, Schoof and Anslow2013). As shown in Figure 8, the exact thickness is discontinuous at the cliff, as it goes to zero on the uphill side and has a non-zero value on the downhill side. Note that our computation uses two horizontal dimensions, but it is constant in the y-direction (not shown).

Fig. 8. Results from
![]() ${M^{\rm \star}} $
method, and its upwinding variations with different λ values in formula (30), compared with the bedrock-step exact solution, on a Δx = 1000 m grid. The bedrock itself is shown with a thick solid line.
${M^{\rm \star}} $
method, and its upwinding variations with different λ values in formula (30), compared with the bedrock-step exact solution, on a Δx = 1000 m grid. The bedrock itself is shown with a thick solid line.
Figure 8 shows results both from
![]() ${M^{\rm \star}} $
calculations and additional calculations without upwinding (‘λ = 0’) and using the maximum upwind that does not expand the stencil (‘λ = 1’) (Eqn (30)). These results suggest why we have chosen λ = 1/4 in
${M^{\rm \star}} $
calculations and additional calculations without upwinding (‘λ = 0’) and using the maximum upwind that does not expand the stencil (‘λ = 1’) (Eqn (30)). These results suggest why we have chosen λ = 1/4 in
![]() ${M^{\rm \star}} $
. For λ = 0 there are large errors on the downhill side of the cliff, while for λ = 1 the uphill thickness is too large. Just a bit of upwinding captures the flux at the cliff, so that both uphill and downhill thicknesses are good.
${M^{\rm \star}} $
. For λ = 0 there are large errors on the downhill side of the cliff, while for λ = 1 the uphill thickness is too large. Just a bit of upwinding captures the flux at the cliff, so that both uphill and downhill thicknesses are good.
To compare with results of Jarosch and others (Reference Jarosch, Schoof and Anslow2013), we applied the
![]() ${M^{\rm \star}} $
method on grids with Δx = Δy = 1000, 500, 250, 125 m. When we measure maximum thickness errors (not shown), there is no evidence of convergence as the grid is refined. However, maximum errors are not expected to decay. (This is because merely interpolating a discontinuous function like the exact solution with piecewise-linear functions generates large errors in the maximum norm.) For average thickness errors the evidence of convergence is unconvincing (not shown). The standard theory of FE methods also does not ensure convergence in average error, because of the extremely low regularity of the exact solution (Elman and others, Reference Elman, Silvester and Wathen2005). In any case, error norms are not reported by Jarosch and others (Reference Jarosch, Schoof and Anslow2013), so we cannot compare with that source.
${M^{\rm \star}} $
method on grids with Δx = Δy = 1000, 500, 250, 125 m. When we measure maximum thickness errors (not shown), there is no evidence of convergence as the grid is refined. However, maximum errors are not expected to decay. (This is because merely interpolating a discontinuous function like the exact solution with piecewise-linear functions generates large errors in the maximum norm.) For average thickness errors the evidence of convergence is unconvincing (not shown). The standard theory of FE methods also does not ensure convergence in average error, because of the extremely low regularity of the exact solution (Elman and others, Reference Elman, Silvester and Wathen2005). In any case, error norms are not reported by Jarosch and others (Reference Jarosch, Schoof and Anslow2013), so we cannot compare with that source.
However, like Jarosch and others (Reference Jarosch, Schoof and Anslow2013) we can examine relative volume error, a weak quality measure, in addition to the visual evidence from Figure 8. Table 1 shows the value
Table 1. Relative volume difference percentages Eqn (41) on the bedrock-step exact solution. ‘
![]() ${M^{\rm \star}} $
’, ‘λ = 0’ and ‘λ = 1’ columns show the same three upwinding variations as in Figure 8. ‘NC’ indicates a Newton-iteration convergence failure. ‘Superbee’ and ‘M2’ columns are from Jarosch and others (Reference Jarosch, Schoof and Anslow2013)
${M^{\rm \star}} $
’, ‘λ = 0’ and ‘λ = 1’ columns show the same three upwinding variations as in Figure 8. ‘NC’ indicates a Newton-iteration convergence failure. ‘Superbee’ and ‘M2’ columns are from Jarosch and others (Reference Jarosch, Schoof and Anslow2013)

The second, third and fourth columns are from the same three versions of the
![]() ${M^{\rm \star}} $
method shown in Figure 8. Again we see why λ = 1/4 is preferred to the upwinding alternatives. The last two columns of Table 1 show the results reported by Jarosch and others (Reference Jarosch, Schoof and Anslow2013) for their best ‘Superbee’-limited MUSCL scheme and for their implementation of the classical Mahaffy scheme (‘M2’). Thus, we see that results from our implicit, first-order-upwinding
${M^{\rm \star}} $
method shown in Figure 8. Again we see why λ = 1/4 is preferred to the upwinding alternatives. The last two columns of Table 1 show the results reported by Jarosch and others (Reference Jarosch, Schoof and Anslow2013) for their best ‘Superbee’-limited MUSCL scheme and for their implementation of the classical Mahaffy scheme (‘M2’). Thus, we see that results from our implicit, first-order-upwinding
![]() ${M^{\rm \star}} $
scheme are highly satisfactory in this case.
${M^{\rm \star}} $
scheme are highly satisfactory in this case.
4.2. Greenland: bed topography and robustness
While we have demonstrated its effectiveness on verification cases, the method's success ultimately depends on robust convergence when the data of the problem, especially the bed topography b, are realistically rough. To test robustness and high-resolution scalability we use two Greenland ice sheet bed topography datasets of different smoothness. We see that runs at high resolution (600–2000 m) converge only imperfectly on the rougher data, but that implicit time steps can be used to get arbitrarily close to steady state in such cases.
The smoother and older BEDMAP1 bed data are on a 5 km grid (Bamber and others, Reference Bamber, Layberry and Gogenini2001); we call it ‘ BM1 ’. Along with a gridded model for present-day surface mass balance (Ettema and others, Reference Ettema2009), which all of our experiments use, it is included in the SeaRISE data (Bindschadler and others, Reference Bindschadler2013). The newer, finer-resolution, and rougher-bed data, on a 150 m grid, are from Morlighem and others (Reference Morlighem, Rignot, Mouginot, Seroussi and Larour2014). This dataset, which we call ‘ MCB ’, is generated by mass-conservation methods using both recent surface velocity measurements and a larger collection of ice-penetrating radar flightlines than were used for BM1 .
Considering the BM1 bed first, we solved the problem on 5000, 2500, 1667, 1250, 1000 and 625 m grids. In the sub-5 km cases, we refined the data using bilinear interpolation, and thus the bed became smoother under grid refinement. Figure 9 shows that, though the Newton solver does not converge at the final ε12 = 0 level, the next-best level ε11 is reached by the continuation scheme using the RS solver (see below) on all of the finer (<2000 m) grids. (It is unlikely that the slightly regularized SIA model at the ε11 continuation level has any deficiencies whatsoever, as a model of real ice dynamics, relative to the unmodified ε12 = 0 SIA model.)

Fig. 9. Smallest successful value of ε i for which the Newton iteration converges on the steady-state problem; lower is better. Different bed data sources ( BM1 or MCB ) and complementarity-problem solvers ( RS or SS ) are compared.
The runs using the MCB data were on 4500, 3000, 1500, 1200, 900 and 600 m grids. The bed elevations were averaged versions of the original 150 m postings, namely onto 30 × 30 blocks for the 9 km grid down to 4 × 4 blocks for the 600 m grid. Because this process reveals more and more detail, the bed became rougher under grid refinement. Except on the coarsest and most-averaged grid, the continuation scheme fails to generate convergent Newton solutions beyond the middle stages (ε4−ε6). Thus, it is clear that highly resolved bed, which causes large and irregular values of D and W to arise from formulas (3) and (6), respectively, limits the success of our combined continuation scheme and Newton iteration.
Though theoretical guidance on the choice of a solver for complementarity problems is, to our knowledge, lacking in this context, these Greenland datasets are realistic and challenging cases on which to compare the two available methods for solving Eqn (32). From Figure 9 it is clear that the convergence of the RS and SS methods (Benson and Munson, Reference Benson and Munson2006) is comparable, with the RS method slightly better in the high-resolution cases. However, the SS method is also three times slower on average over all runs in Figure 9.
Based on these initial experiments we implemented the following strategy for computing the steady-state solution using the MCB bed data averaged onto a 900 m grid and the RS solver: generate five smoothed versions of the bed data, with successively greater averaging before interpolating to the same 900 m grid; the least-smoothed of these data is the simple average of 6 × 6 blocks of the original 150 m data. At the first stage, compute the steady state using the most-smoothed version of the bed data, for which we expect convergence to a ‘good’ level (e.g. ε i < 10−3 such as ε10−ε12). Extract the surface elevation from the result and construct a new initial thickness from it using the next less-smoothed version of the bed data. Though the steady-state continuation/Newton scheme will not converge from this new initial thickness, as convergence is quite insensitive to initial iterate, as it is blocked by bed roughness, one can expect a backward-Euler time step Eqn (40) to converge. Thus, we now start time-stepping. These implicit time steps are chosen sufficiently short so that the continuation scheme fully converges (i.e. to the ε12 = 0 level), and thus we further approach steady state on the better bed. We iterate this bed-resolving strategy through the stages until using the least-smoothed bed, that is, the fully resolved bed on the 900 m grid. We can then continue time-stepping so as to approach steady state as closely as desired.
The result of this strategy is shown in Figure 10. The first step was a nearly converged steady-state computation (ε11 level) on the most-smoothed bed. The five-step bed-resolving process in the last paragraph was applied using very short (~10−3 years) backward Euler time steps. Then 50 model years of additional backward Euler time steps were run, with 1 month time steps (0.1 years) for the last 20 years. The result in Figure 10 has volume 3.48 × 106 km3; compare the observed value, 2.95 × 106. The average absolute thickness error of 139 m is dominated by large errors from mislocating the ice margin in fjord-like coastal areas. Though the average diffusivity over the whole ice sheet was small (D ≈ 0.5 m2 s−1), maximum values of D ≈ 6 × 103 m2 s−1 occurred in the interiors of highly resolved outlet glaciers.

Fig. 10. Computed high-resolution ice sheet surface. The free boundary (margin) is determined only by the surface mass balance, bedrock topography and the steady-state, simplified-dynamics SIA model. We use 900 m model resolution and the MCB bed topography data.
5. DISCUSSION AND CONCLUSION
The problem solved in this paper is fundamentally different from most prior ice-sheet modeling. The steady-state geometry and extent of an ice sheet are computed directly as a function of only two datasets, namely the bed topography and surface mass balance. Though this function has not been proved to be well defined, even in the elevation-independent surface mass-balance cases here (compare Jouvet and others, Reference Jouvet, Rappaz, Bueler and Blatter2011), there is theoretical support for wellposedness (Jouvet and Bueler, Reference Jouvet and Bueler2012) and nothing seen in our calculations suggests otherwise.
We do not claim that the model here, an untuned isothermal SIA model using EISMINT I parameter values, is sufficiently complete to represent all of the important physics of the Greenland ice sheet. By contrast, thermomechanically coupled shallow ‘hybrid’ models that include membrane stresses in the stress balance are indeed capable of very-high-quality match to the observations (Aschwanden and others, Reference Aschwanden, Fahnestock and Truffer2016).
Our numerical methods are based on both new and old ideas. The numerical discretization of the SIA equation starts from a classical structured-grid FD scheme (Mahaffy, Reference Mahaffy1976), but we make two improvements to create the new
![]() ${M^{\rm \star}} $
scheme, both based on reinterpreting the classical scheme as an FVE method:
${M^{\rm \star}} $
scheme, both based on reinterpreting the classical scheme as an FVE method:
-
(1) improved quadrature in the flux integral, and
-
(2) first-order upwinding for the part of the ice flux which is proportional to the bed gradient.
Then, because the constraint of non-negative thickness makes this a free-boundary problem, we put it in non-linear complementarity problem form and apply a parallel Newton solver designed for such problems.
In verification cases, the
![]() ${M^{\rm \star}} $
method is both more accurate than, and gives substantially better Newton iteration convergence than, the classical scheme. We also show that the method can succeed at large scale and high resolution on real, highly irregular ice-sheet bed elevation data. Compared with the steady-state Greenland calculation by Jouvet and Bueler (Reference Jouvet and Bueler2012), we have increased the number of unknowns by more than an order of magnitude, and we replaced a fixed-point iteration by a quadratically convergent Newton method.
${M^{\rm \star}} $
method is both more accurate than, and gives substantially better Newton iteration convergence than, the classical scheme. We also show that the method can succeed at large scale and high resolution on real, highly irregular ice-sheet bed elevation data. Compared with the steady-state Greenland calculation by Jouvet and Bueler (Reference Jouvet and Bueler2012), we have increased the number of unknowns by more than an order of magnitude, and we replaced a fixed-point iteration by a quadratically convergent Newton method.
Convergence of the Newton iteration in the presence of finely resolved, and thus very rough, bed is not guaranteed. Highly variable values of diffusivity D, such as those that arise in the computation that generated Figure 10 apparently form part of the barrier to full convergence of the continuation/Newton scheme for such steady-state computations. The convergence of long time steps on rough beds is also limited, but this was not studied quantitatively. A complete and/or precise understanding of the failure of convergence of the Newton iteration on rough beds is a topic for further research.
Though we have not tested it, the
![]() ${M^{\rm \star}} $
ideas can be extended to unstructured dual Delaunay/Voronoi meshes such as those used by Egholm and Nielsen, (Reference Egholm and Nielsen2010) and the MPAS Land Ice model (COSIM Team, 2013; Ringler and others, Reference Ringler, Petersen, Higdon, Jacobsen, Jones and Maltrud2013). These models use P
1 FEs on a Delaunay triangulation and flux-integral quadrature on the Voronoi-cell edges. The improved quadrature idea (1) above would split the cell edges where the element (i.e. triangle) boundaries cross them, while the upwinding idea (2) requires interpretation as a first-order reconstruction after advection. Such a method would improve on that of Egholm and Nielsen (Reference Egholm and Nielsen2010), in particular, by exploiting an underlying P
1 element flux approximation, instead of using a highly averaging and stencil-expanding least squares method.
${M^{\rm \star}} $
ideas can be extended to unstructured dual Delaunay/Voronoi meshes such as those used by Egholm and Nielsen, (Reference Egholm and Nielsen2010) and the MPAS Land Ice model (COSIM Team, 2013; Ringler and others, Reference Ringler, Petersen, Higdon, Jacobsen, Jones and Maltrud2013). These models use P
1 FEs on a Delaunay triangulation and flux-integral quadrature on the Voronoi-cell edges. The improved quadrature idea (1) above would split the cell edges where the element (i.e. triangle) boundaries cross them, while the upwinding idea (2) requires interpretation as a first-order reconstruction after advection. Such a method would improve on that of Egholm and Nielsen (Reference Egholm and Nielsen2010), in particular, by exploiting an underlying P
1 element flux approximation, instead of using a highly averaging and stencil-expanding least squares method.
The most important extension of our work, however, depends on noticing that it is actually rather flux-agnostic. In particular, the steady-state mass-conservation Eqn (7) or (8) also applies as stated with any Stokes (Greve and Blatter, Reference Greve and Blatter2009), ‘higher-order’ (Pattyn and others, Reference Pattyn2008) or hybrid membrane-stress-resolving (Winkelmann and others, Reference Winkelmann2011) model that computes the ice-sheet geometry. In such models, the computation of the discrete flux
![]() ${{{\bf q}}^h}$
from the approximate ice-sheet thickness H
h
is completely different from the direct differentiation done here in the SIA, as it involves solving a separate elliptic-type stress balance model. For structured-grid models, however, the same basic FVE method (Eqns (26–28)) sets up the discrete equations. Then the problem becomes a version of complementarity problem (32), as ice thickness is non-negative regardless of the model for its stresses. Thereby one is faced with a free-boundary problem for the steady-state ice-sheet geometry. An adapted Newton solver is the natural choice to solve such problems; the residual evaluation in such cases always includes some kind of computation of
${{{\bf q}}^h}$
from the approximate ice-sheet thickness H
h
is completely different from the direct differentiation done here in the SIA, as it involves solving a separate elliptic-type stress balance model. For structured-grid models, however, the same basic FVE method (Eqns (26–28)) sets up the discrete equations. Then the problem becomes a version of complementarity problem (32), as ice thickness is non-negative regardless of the model for its stresses. Thereby one is faced with a free-boundary problem for the steady-state ice-sheet geometry. An adapted Newton solver is the natural choice to solve such problems; the residual evaluation in such cases always includes some kind of computation of
![]() ${{{\bf q}}^h}$
from H
h
, however complicated. While the roughness of the bed is also a difficulty in solving such ‘higher-order’ stress-balance problems (Brown and others, Reference Brown, Smith and Ahmadia2013), the spatial integration used in all membrane-stress or full-stress resolving models should actually smooth the residual function seen by the Newton solver. To our knowledge, however, direct solution of steady-state Eqn (7) has not been attempted for other than SIA fluxes. Clearly, these are topics for further research.
${{{\bf q}}^h}$
from H
h
, however complicated. While the roughness of the bed is also a difficulty in solving such ‘higher-order’ stress-balance problems (Brown and others, Reference Brown, Smith and Ahmadia2013), the spatial integration used in all membrane-stress or full-stress resolving models should actually smooth the residual function seen by the Newton solver. To our knowledge, however, direct solution of steady-state Eqn (7) has not been attempted for other than SIA fluxes. Clearly, these are topics for further research.
ACKNOWLEDGEMENTS
Thanks to Scientific Editor R. Greve and reviewers A. Jarosch and G. Jouvet for helpful comments, which improved the presentation and content. Thanks also to B. Smith of Argonne National Laboratory for key help on the PETSc solvers. This work was supported by NASA grant #NNX13AM16G and a grant of high-performance computing resources from the Arctic Region Supercomputing Center.
APPENDIX
ANALYTICAL JACOBIAN
To sketch the calculation of the analytical Jacobian for the
![]() ${M^{\rm \star}} $
method, we first recall that each Eqn (31) comes from Eqn (26),
${M^{\rm \star}} $
method, we first recall that each Eqn (31) comes from Eqn (26),
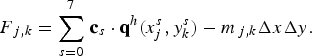 $${F_{\,j,k}} = \sum\limits_{s = 0}^7\,{{{\bf c}}_s} \cdot {{{\bf q}}^h}(x_j^s, y_k^s ) - {m_{\,j,k}}\Delta x\Delta y.$$
$${F_{\,j,k}} = \sum\limits_{s = 0}^7\,{{{\bf c}}_s} \cdot {{{\bf q}}^h}(x_j^s, y_k^s ) - {m_{\,j,k}}\Delta x\Delta y.$$
As the stencil of the
![]() ${M^{\rm \star}} $
scheme is the nine-node box shown in Figure 1b, each row of the Jacobian has nine non-zero entries corresponding to locations p, q where F
j,k
depends on H
p,q
. We compute
${M^{\rm \star}} $
scheme is the nine-node box shown in Figure 1b, each row of the Jacobian has nine non-zero entries corresponding to locations p, q where F
j,k
depends on H
p,q
. We compute
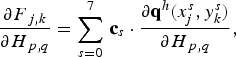 $$\displaystyle{{\partial {F_{\,j,k}}} \over {\partial {H_{\,p,q}}}} = \sum\limits_{s = 0}^7\,{{{\bf c}}_s} \cdot \displaystyle{{\partial {{{\bf q}}^h}(x_j^s, y_k^s )} \over {\partial {H_{\,p,q}}}},$$
$$\displaystyle{{\partial {F_{\,j,k}}} \over {\partial {H_{\,p,q}}}} = \sum\limits_{s = 0}^7\,{{{\bf c}}_s} \cdot \displaystyle{{\partial {{{\bf q}}^h}(x_j^s, y_k^s )} \over {\partial {H_{\,p,q}}}},$$
noting that
![]() $\partial {{{\bf q}}^h}(x_j^s, y_k^s )/\partial {H_{p,q}}$
is non-zero only if H
p,q
is one of the four nodal values on the element
$\partial {{{\bf q}}^h}(x_j^s, y_k^s )/\partial {H_{p,q}}$
is non-zero only if H
p,q
is one of the four nodal values on the element
![]() ${{\rm \squ} _{u,v}}$
containing the quadrature point
${{\rm \squ} _{u,v}}$
containing the quadrature point
![]() $(x_j^s, y_k^s )$
. Using index ℓ = 0, 1, 2, 3 for the corners of rectangle
$(x_j^s, y_k^s )$
. Using index ℓ = 0, 1, 2, 3 for the corners of rectangle
![]() ${{\rm \squ} _{u,v}}$
, we need to write code to compute
${{\rm \squ} _{u,v}}$
, we need to write code to compute
 $${{\bf Q}}_\ell ^s = \displaystyle{{\partial {{{\bf q}}^h}(x_j^s, y_k^s )} \over {\partial {H_\ell}}}$$
$${{\bf Q}}_\ell ^s = \displaystyle{{\partial {{{\bf q}}^h}(x_j^s, y_k^s )} \over {\partial {H_\ell}}}$$
when
![]() $(x_j^s, y_k^s )$
is in
$(x_j^s, y_k^s )$
is in
![]() ${{\rm \squ} _{u,v}}$
.
${{\rm \squ} _{u,v}}$
.
Derivatives are easiest to compute, in a Q
1 FE method, using local coordinates ξ = (x − x
u
)/Δx and η = (y − y
v
)/Δy on
![]() ${{\rm \squ} _{u,v}}$
, so that 0 ≤ ξ, η ≤ 1. Bilinear interpolation defines a function H
u,v
= H
u,v
(ξ, η) on
${{\rm \squ} _{u,v}}$
, so that 0 ≤ ξ, η ≤ 1. Bilinear interpolation defines a function H
u,v
= H
u,v
(ξ, η) on
![]() ${{\rm \squ} _{u,v}}$
from interpolation of the four nodal values H
ℓ, and bed elevation function b
u,v
is similarly defined. Differentiation with respect to ξ and η gives vector-valued functions
${{\rm \squ} _{u,v}}$
from interpolation of the four nodal values H
ℓ, and bed elevation function b
u,v
is similarly defined. Differentiation with respect to ξ and η gives vector-valued functions
![]() ${(\nabla H)_{u,v}}$
and
${(\nabla H)_{u,v}}$
and
![]() ${(\nabla b)_{u,v}}$
. Differentiation with respect to H
ℓ gives the scalar function ∂H
u,v
/∂H
ℓ and vector-valued function
${(\nabla b)_{u,v}}$
. Differentiation with respect to H
ℓ gives the scalar function ∂H
u,v
/∂H
ℓ and vector-valued function
![]() $\partial {(\nabla H)_{u,v}}/\partial {H_\ell} $
. We write code for each of these (ξ, η)-dependent functions on
$\partial {(\nabla H)_{u,v}}/\partial {H_\ell} $
. We write code for each of these (ξ, η)-dependent functions on
![]() ${{\rm \squ} _{u,v}}$
. Then we write code to compute functions D
u,v
and ∂D
u,v
/∂H
ℓ from Eqn (3), and then
${{\rm \squ} _{u,v}}$
. Then we write code to compute functions D
u,v
and ∂D
u,v
/∂H
ℓ from Eqn (3), and then
![]() ${{{\bf W}}_{u,v}}$
and
${{{\bf W}}_{u,v}}$
and
![]() $\partial {{{\bf W}}_{u,v}}/\partial {H_\ell} $
from Eqn (6), in local coordinates ξ, η on
$\partial {{{\bf W}}_{u,v}}/\partial {H_\ell} $
from Eqn (6), in local coordinates ξ, η on
![]() ${{\rm \squ} _{u,v}}$
.
${{\rm \squ} _{u,v}}$
.
Denote local coordinates of the quadrature point
![]() $(x_j^s, y_k^s )$
on element
$(x_j^s, y_k^s )$
on element
![]() ${{\rm \squ} _{u,v}}$
by
${{\rm \squ} _{u,v}}$
by
![]() ${\xi ^s} = (x_j^s - {x_u})/\Delta x$
and
${\xi ^s} = (x_j^s - {x_u})/\Delta x$
and
![]() ${\eta ^s} = (y_k^s - {y_v})/\Delta y$
. Note that for each quadrature point, as in Figure 4, upwinding determines an additional evaluation point, whose local coordinates are denoted
${\eta ^s} = (y_k^s - {y_v})/\Delta y$
. Note that for each quadrature point, as in Figure 4, upwinding determines an additional evaluation point, whose local coordinates are denoted
![]() $(\xi _{{\rm up}}^s, \eta _{{\rm up}}^s )$
. In these terms, from Eqn (6), for the evaluation of the residual, Eqn (A1), and for the evaluation of the Jacobian entries, Eqn (A2), we write code to compute
$(\xi _{{\rm up}}^s, \eta _{{\rm up}}^s )$
. In these terms, from Eqn (6), for the evaluation of the residual, Eqn (A1), and for the evaluation of the Jacobian entries, Eqn (A2), we write code to compute
 $$\eqalign{{{{\bf q}}^h}(x_j^s, y_k^s ) = & - {D_{u,v}}({\xi ^s},{\eta ^s})(\nabla H{)_{u,v}}({\xi ^s},{\eta ^s}) \cr & + {{{\bf W}}_{u,v}}({\xi ^s},{\eta ^s}){H_{u,v}}{(\xi _{{\rm up}}^s, \eta _{{\rm up}}^s )^{n + 2}},}$$
$$\eqalign{{{{\bf q}}^h}(x_j^s, y_k^s ) = & - {D_{u,v}}({\xi ^s},{\eta ^s})(\nabla H{)_{u,v}}({\xi ^s},{\eta ^s}) \cr & + {{{\bf W}}_{u,v}}({\xi ^s},{\eta ^s}){H_{u,v}}{(\xi _{{\rm up}}^s, \eta _{{\rm up}}^s )^{n + 2}},}$$
 $$\eqalign{{{\bf Q}}_\ell ^s = & - \displaystyle{{\partial {D_{u,v}}} \over {\partial {H_\ell}}} ({\xi ^s},{\eta ^s})(\nabla H{)_{u,v}}({\xi ^s},{\eta ^s}) \cr & - {D_{u,v}}({\xi ^s},{\eta ^s})\displaystyle{{\partial {{(\nabla H)}_{u,v}}} \over {\partial {H_\ell}}} ({\xi ^s},{\eta ^s}) \cr & + \displaystyle{{\partial {{{\bf W}}_{u,v}}} \over {\partial {H_\ell}}} ({\xi ^s},{\eta ^s}){H_{u,v}}{(\xi _{{\rm up}}^s, \eta _{{\rm up}}^s )^{n + 2}} \cr & + (n + 2){{{\bf W}}_{u,v}}({\xi ^s},{\eta ^s}){H_{u,v}}{(\xi _{{\rm up}}^s, \eta _{{\rm up}}^s )^{n + 1}} \cr & \quad \cdot \displaystyle{{\partial {{(\nabla H)}_{u,v}}} \over {\partial {H_\ell}}} (\xi _{{\rm up}}^s, \eta _{{\rm up}}^s ).}$$
$$\eqalign{{{\bf Q}}_\ell ^s = & - \displaystyle{{\partial {D_{u,v}}} \over {\partial {H_\ell}}} ({\xi ^s},{\eta ^s})(\nabla H{)_{u,v}}({\xi ^s},{\eta ^s}) \cr & - {D_{u,v}}({\xi ^s},{\eta ^s})\displaystyle{{\partial {{(\nabla H)}_{u,v}}} \over {\partial {H_\ell}}} ({\xi ^s},{\eta ^s}) \cr & + \displaystyle{{\partial {{{\bf W}}_{u,v}}} \over {\partial {H_\ell}}} ({\xi ^s},{\eta ^s}){H_{u,v}}{(\xi _{{\rm up}}^s, \eta _{{\rm up}}^s )^{n + 2}} \cr & + (n + 2){{{\bf W}}_{u,v}}({\xi ^s},{\eta ^s}){H_{u,v}}{(\xi _{{\rm up}}^s, \eta _{{\rm up}}^s )^{n + 1}} \cr & \quad \cdot \displaystyle{{\partial {{(\nabla H)}_{u,v}}} \over {\partial {H_\ell}}} (\xi _{{\rm up}}^s, \eta _{{\rm up}}^s ).}$$













