Introduction
Reference NyeNye (1970) and Reference KambKamb (1970) give the expression for the basal shear stress τ b (equation (4), Reference NyeNye (1970))

where γ(v) is the power spectral density of microrelief and
In these equations L is the latent heat of fusion, C is the constant relating the depression of the melting-point to the pressure, K is the mean thermal conductivity of ice and rock, ƞ is the effective viscosity of the ice, u is the ice velocity, and v is the wave number of the microrelief. This relation applies (Reference KambKamb, 1970; Reference LliboutryLliboutry, 1975) if the ice has a non-linear viscosity and if there is no cavitation. In such a case, the spectral power density of microrelief is a very important parameter in the study of glacier sliding.
Observation of glacial bedrock shows that tiny cavities, a few centimetres long, appear at the interface between the ice and the rock. At Blue Glacier, a four-centimetre cavity has been observed under 119 m of ice (Reference KambKamb, 1970). Reference LliboutryLliboutry (1968) has shown the importance of the shadowing function for the study of sliding with cavitation. In this case τ b is given by equation (1–16) of Reference Benoist and LliboutryBenoist and Lliboutry (1978)

where ρ ∞ is the mean pressure of ice against bed, and ρ is the pressure when cavitation is absent. S(t) is the shadowing function of bedrock and t the mean slope of the ceiling of the cavities. If cavitation occurs, the bedrock shadowing function becomes the most important geometrical parameter.
In this paper, the preliminary results of a statistical and spectral analysis of glacial bedrock are given. Only profiles levelled in the mean direction of ice flow deduced from striations on rock are studied. For each profile the spectral power density and shadowing function are given. As the shadowing function depends on the distribution of elevations and profile slopes (Reference Benoist and LliboutryBenoist and Lliboutry, 1978), these distributions are also studied.
The sampling interval, the method used for the spectral analysis, and the available data determine the bandwidth which can be studied, and the frequency v∗ given by Equation (2) is of the order of a few decimetres. Thus, only the wavelengths between 3.6 and 40 cm will be analysed, for reasons which will be discussed later.
Fieldwork
The profiles which were studied are near the snout of Glacier de Saint-Sorlin (Massif des Grandes Rousses, France) in the contact area between arkoses and carboniferous schists; therefore, these two formations can be found in the same profile. The drift deposited by the receding glacier was removed from three areas numbered I, II, and III. Zone I is a very smooth area with large undulations (≈ 5 m long). Four separate longitudinal profiles (≈ 15 m long) were taken in this area. Zone II is composed of elongated bumps (≈ 2 m long) in the direction of ice flow, separated by deep channels with striations at their bases: this zone can really be referred to as an area of roches moutonnées. The appearance of zone III is intermediate between the appearance of the first and the second zone. Two profiles (≈ 20 m long) were levelled in this area.
Measurements were taken vertically every centimetre between a reference horizontal and the rock. The levelling device consisted of a beam two metres long supported at each end by a tripod and a carriage which supported a vertical rule. The beam was levelled with an accurate spirit level. The accuracy and reproducibility of the measurements were good, vertical accuracy is ±0.5 mm and horizontal accuracy is better than 0.1 mm.
This simple, precise method has three disadvantages: it is not suitable for the study of long wavelengths, it is not readily applicable to the two-dimensional problem, and a considerable amount of time is necessary to level 10 000 points in the field (this amount of data is a working minimum for our data analysis). For these reasons, photogrammetry has been employed; it is less accurate but it does not have these disadvantages. Data are acquired using a stereo-comparator. Results obtained by this method will be published later.
Filtering of large wavelengths
As explained by Reference NyeNye (1970), microrelief must be defined relative to a smoothed bedrock, the reference profile. To obtain this, low frequencies must be removed from the actual profile. Since all information about frequencies higher than (2Δx)–1 (Δx is the sampling interval) is lost in the data digitization, a numerical bandpass filter was used. This gives a better stability than with a high-pass filter. The procedure needed to define a bandpass filter from its transfer function is described by Reference RadixRadix (1970).
The 3 dB low cut-off frequency is 0.01 cm–1. In order to reduce spurious response the high cut-off frequency is 0.4 cm–1. The transient response of this bandpass filter vanishes at x ═ 120 cm which means that the first 120 points of each filtered profile correspond to the transient response and they will have to be removed from the profile before analysis. The gain is constant from ν 1 ═ 0.025 cm–1 to ν 2 ═ 0.275 cm–1. Thus, in the spectral analysis, only the frequencies between ν 1 and ν 2 will have to be considered in the interpretation. The frequencies lower than v 1 constitute the general topography of the reference bedrock.
Statistical Distribution of Elevations and Slopes
Results of the distributions of elevations are collected in Table I. The first four moments and the standard deviation of the first three moments have been computed for each profile.
Table I. Statistical study of levels

Plotting the results on Gaussian (normalized) paper shows that the elevation distributions of the profiles are not Gaussian. For each zone, variances have been tested to establish whether the different profiles could be considered as samples of the same set. For zones I and II, these tests are positive with 99% confidence limits. On the other hand, the two profiles of zone III must be considered separately, the difference of their variances being significant. They will be named zone III-1 and zone III-2. The difference between the two profiles of the third area could be produced by the anisotropy of bedrock. Only a two-dimensional study of bedrock can explain what has happened in this zone.
According to the theory Reference Hald(Hald, 1952), if a distribution is not Gaussian, then all the moments, up to a high order, must be tested to examine whether the samples have been selected from a single population. However, accuracy decreases rapidly with increasing order because the number of individuals in the samples is not large enough. In practice, a stability to degree two is sufficient.
If we take the inaccuracy into account, μ1 and μ3 do not differ significantly from zero. The distributions of ordinates are then quite symmetrical. The following values will be used:
-
zone I μ1 ═ 0, μ2 ═ 1.092, σ μ2 ═ 0.025, β2 ═ 4.20,
-
zone II μ1 ═ 0, μ2 ═ 2.08, σ μ2 ═ 0.09, β2 ═ 4.5.
Coefficient β 2 ═ μ 4/μ 2 2 is the flatness coefficient for the distribution. It is equal to three for a Gaussian distribution. Values greater than three are associated with distributions which are sharper than a Gaussian curve with the same standard deviation (a leptokurtic distribution).
For each profile, slopes at point j have been estimated by
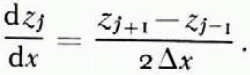
Results of slope distributions are given in Table II. The same verifying tests as for the elevations have been carried out. The conclusions are the same, for zone I and II profiles come from the same population, but profiles of zone III come from different populations,
-
zone I μ1 ═ 0, μ2 ═ 0.031, σ μ2 ═ 0.001, μ3 ═ 0, β2 ═ 8.74,
-
zone II μ1 ═ 0, μ2 ═ 0.051, σ μ2 ═ 0.003, μ3 ═ 0, β2 ═ 6.15.
Table II. Statistical study of slopes

Distributions are symmetric and leptokurtic. A symmetric distribution of slopes in roches moutonnées may be surprising, but it is at the scale of one metre that their asymmetry appears—the microrelief is studied here at the scale of one decimetre.
These results are very important in the study of the shadowing function and the spectral analysis. For zone I and II treated separately, the profiles come from the same statistical process and it becomes possible to average the estimated values of shadowing function or the spectral power density. This averaging improves the accuracy of the estimations.
Spectral analysis
Two methods can be chosen to compute the spectral power density: the classical method, which is to compute the discrete Fourier transform (D.F.T.), or the maximum entropy method (M.E.M.) (Reference Smylie, Smylie, Clarke and UlrychSmylie and others, 1973). M.E.M. is more attractive than the classical methods because it gives results for wavelengths longer than the profile length, also, the sharpness of the analysis is better, but the method has many disadvantages, in some cases split peaks appear (Reference Fougere, Fougere, Zawalick and RadoskiFougère and others, 1976), the variance of estimated power spectral density is not known, and the computation is faster when using a fast Fourier transform algorithm than when using the M.E.M. For these reasons, I chose the classical method.
Let sequence zk (k ═ 0 to M – 1) be the sequence of the profile z(x) which has been sampled at an interval Δx. The discrete Fourier transform of sequence Zk is sequence Zl (l ═ 0 to M – 1) defined by the equation

The D.F.T. has been computed with a fast Fourier transform algorithm (Reference EberhardEberhard, unpublished). An estimate of spectral power density γl is given by
(where the circumflex ˆ indicates the estimate of a parameter).
With the above formulae, Parseval’s theorem becomes

(The moment of order two measures the power of a signal.)
It can be shown (Reference Oppenheim and SchaferOppenheim and Schafer, 1975) that this estimator of spectral power density is not consistent, the variance does not tend to zero as the number of observations becomes large. Welch’s method (Reference Oppenheim and SchaferOppenheim and Schafer, 1975) has been used as a better estimator of spectral power density.
The whole sequence Zk is cut in N independent slices of M points. The mean of the various estimates for spectral power densities gives a final estimate γ t. The variance of γ t is given by

To reduce the side lobes of the response, the spectra have been filtered with Hamming’s window (Reference BåthBåth, 1974). In order not to lose any information, slices must overlap by one-half. As the number of samples is fixed, this method forces a compromise between the number of slices N and the number of analysed points M in each slice or, in other words, between variance and sharpness of analysis. Fast Fourier transform computation has been performed with slices having. M ═ 128 points. The sharpness of analysis is (Δx ═ 1 cm)

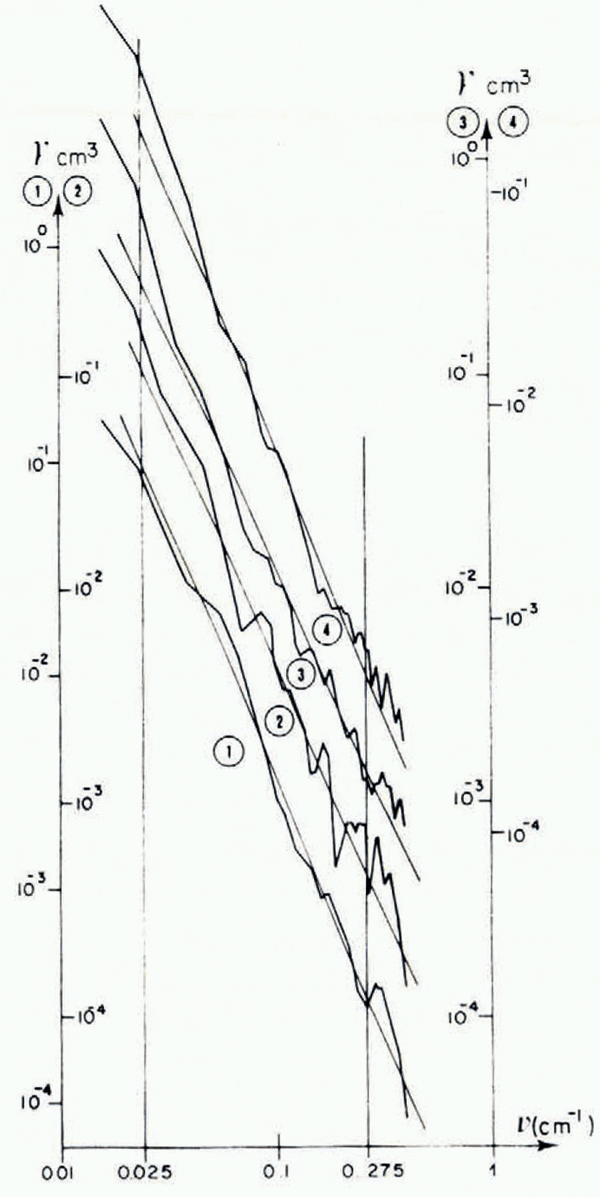
Figure 1 shows the spectral power density γ t estimated by this method plotted with logarithmic coordinates. If the real value of the spectral power density is required, γ t must be multiplied by M ═ 128.

Fig. 1. Spectral power density γ̄(v). ![]() zone I;
zone I; ![]() zone II;
zone II; ![]() zone III-1;
zone III-1; ![]() zone III-2. The vertical line marks the frequency range within which the filter-gain factor is constant (0.025 cm–1 < v < 0.275 cm–1). Straight lines are given by the model y(v) ═ Y
0
v–n
, computed for each zone.
zone III-2. The vertical line marks the frequency range within which the filter-gain factor is constant (0.025 cm–1 < v < 0.275 cm–1). Straight lines are given by the model y(v) ═ Y
0
v–n
, computed for each zone.
In the frequency range 0.025 cm–1 < ν < 0.275 cm–1, spectral power density γ(v) decreases roughly as γ 0 ν–n where ν ═ lΔν (l ═ 0 to M–1). Using a weighted least-square method, each spectrum has been fitted to the linear relation
The weighting function equals the inverse of the standard deviation of log (γ(ν)).
Reference BoisBois (unpublished) gives a method for checking the validity of a linear regression if the distribution of the residues is Gaussian. Residues are the quantities given by
where yi is the measured value at xi and ŷi the value estimated by the linear regression.
Let Ej be the sum of the first j residues

and Υ(j) the ellipse given by
σε is the standard deviation of residues. It is given by
where C is the correlation coefficient between yi and xi . At a given probability threshold f, the curve of Ej against j is inside Υ(j) if the residues are randomly distributed. t(f) is the normal standarized variable of probability 1–f/2(f ═ 1%, t(f) ═ 2.56). (Bois’ results can be found in Reference BernierBernier, 1977.)
For zone I, there are 44 independent estimates of γ(v), the distribution of log (γ(ν)) for a fixed ν value is fairly Gaussian. The model can be tested with the method described by Bois.
Results obtained for the fitted spectra are gathered in Table III. The various estimates of n overlap with 99% confidence and the following mean value will be used:
on the other hand, γ 0 values are different for each zone.
Table III. Results of spectral power density fitting by the model

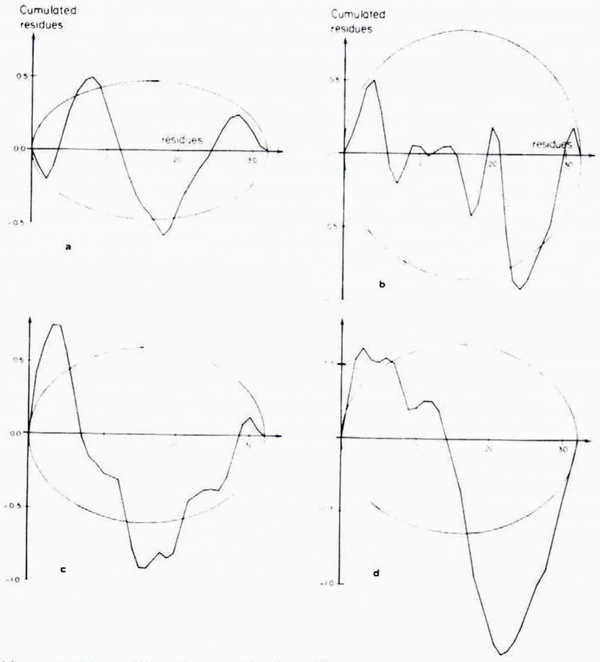
The model explains 99% of the variance, in the frequency range 0.025 cm–1 to 0.275 cm–1, but, assuming that the residues are, in fact, Gaussian, the cumulated residues (Fig. 2) go out of the ellipse constructed for 99% confidence limits. This result can occur for two reasons: the tests may not work because the population is not strictly Gaussian (there are not enough data at present to give a good estimate distribution of log (γ(ν)), or the model may not be adequate to explain the variation of the spectrum, and the tests may be showing a systematic difference between model and spectrum.

Fig. 2. Cumulated residues assuming a Gaussian distribution. Ellipses are drawn for 99% confidence limits: a. zone I; b. zone II; c. zone III-1; d. zone III-2.
Theorists have considered the same model for non-dimensional profiles with n ═ 3. In the frequency range studied here, spectral power density does not decrease as fast as in a non-dimensional model. Reference KambKamb’s model (1970) with a truncated spectrum at short wavelengths seems to be unrealistic. In Table III. estimates of power and of quadratic slope ρ (square root of slope variance) are given in the frequency range 0.025 cm–1< ν < 0.275 cm–1.
The Fourier transform of the derivative of x(t) is 2iπvX(v) where X(v) is the Fourier transform of x(t) Reference Båth(Båth, 1974), therefore, the spectral power density of the slopes γ s(v) is related to the spectral power density of the levels γ(v) by:
To verify the accuracy of this estimation, the power P 1 in the band pass of the filter has been computed. Because of spectral errors and owing to the fact that filtration is not perfect outside of the pass band, the μ2 value, computed in the statistical study (Table I), is found to agree well.
Computation of power can be performed in two ways in the frequency range 0.025 cm–1 < ν < 0.275 cm–1, by using γ values as given by the spectral analysis directly, or by using model γl ═ γ0 (lΔv)–2.36. Results given by the computations are good. The quadratic slopes could be expected to be estimated well if Equation (14) is used, but, unfortunately, the results obtained by this method are very bad. This difference comes from either a breakdown in the proposed model, or it arises from Equation (4) which is used to estimate slopes in the statistical study. It is only when direct computation of spectral slopes is carried out that this point will be clarified.
Shadowing function
Let t be the tangent of the angle made between a beam and the horizontal, it is negative when the light source is up-stream of the profile, positive when it is down-stream. The shadowing function S(t) is the ratio of the profile section which is illuminated with incidence tangent t to the total length.
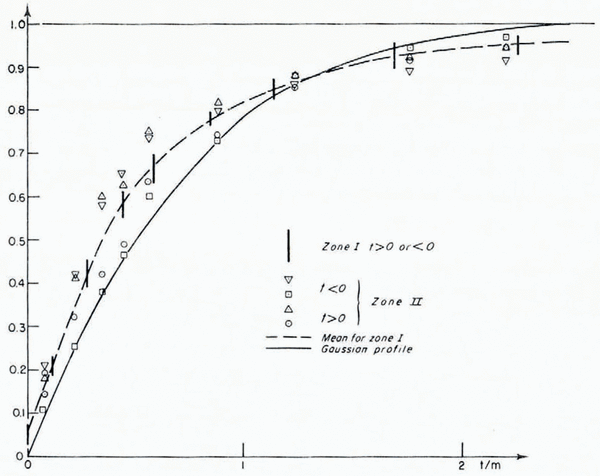
The shadowing function has been computed for profiles in zone I and II using the method described by Reference Benoist and LliboutryBenoist and Lliboutry (1978). Experimental results and the function computed by Reference SmithSmith (1967) for a Gaussian profile are plotted in Figure 3.

Fig. 3. The shadowing Function computed for various cases. Vertical lines along the broken line indicate scattering of estimated values for zone I.
For zone I, the mean curve, drawn by a broken line, has been computed, vertical lines give the dispersion of the estimated shadowing function for this zone. The broken line does not go through the origin because the computational method introduces a systematic error for small angles of incidence. In the early stages of the computation, it is assumed that the first point is illuminated for any angle of incidence. For a given profile, this error increases when vanishes or, for a given t value, it decreases when the total length of the profile increases. In absolute value, for t ═ 0, it is the ratio of the maximum wavelength to twice the length of the profile. In this study, t is approximately 0.05. Fewer results for zone II have been plotted separately, their mean varies along the broken line. Similar results have been obtained for zone III not plotted on Fig. 3).
These results confirm every assumption made previously. There are no important variations when the profile is illuminated in the direction of flow (t < 0) or in reverse direction (t > 0). The distribution of slopes is symmetric. The gap between the broken line and the continuous one is significant. For small t values, S(t/m) is greater than in the Gaussian case, there are more bumps of large size which are illuminated, but, for large incidences, the trend is reversed, there are more hollows in shadow than in the Gaussian case. These results confirm that the distributions are non-Gaussian. The conclusions of Reference Benoist and LliboutryBenoist and Lliboutry (1978) are thus confirmed, the shadowing function of the profile is a function of t/m which depends on the distribution of levels and slopes.
Conclusion
In the frequency range 0.025 cm–1 to 0.275 cm–1, the statistical analysis and a study of the shadowing function shows that the distribution of levels and slopes is symmetric and sharper than the Gaussian distribution with same standard deviation. The shadowing function leads to the assumption that these distributions are independent of the studied area, but this assumption needs to be checked further. The spectral power density γ(v) varies roughly as γ 0 v–n , n ═ 2.36 being the same for all studied zones. γ 0 being a characteristic of the roughness of each area.
It seems that few parameters can quantitatively describe roches moutonnées; among these are the distribution of slopes and levels, the spectral power density, and the shadowing function. To confirm these results, a study of coarse-grained rocks including granites or conglomerates, will be undertaken. A survey of the longer wavelengths using photogrammetry, which may be of particular interest for glacial morphologists, is in progress.
Discussion
B. Hallet: How can you justify choosing to conduct the spectral analysis over such a short wavenumber range? This is particularly problematical in view of the fact that judgement of the important wavenumber range is based on implicit assumptions about the roughness spectrum of the glacier bed. Yet this is precisely what you are documenting in your analysis.
J.-P. Benoist: The controlling obstacle size is found when I compare sliding by plasticity with sliding by melting–refreezing over a sine profile, without the necessity of assuming any continuous spectral power density. Also, the range of wavelengths has been chosen to make the best use of our actual data, making the compromise between the sharpness of analysis and a sufficiently low value of variance of the spectral density estimate.
I. S. Evans: How was the Gaussian profile calculated? What auto-correlation properties were allocated to it?
Benoist: A theoretical calculation of the shadowing function has been made by Reference SmithSmith (1967) assuming a Dirac delta function as the auto-correlation. Reference Benoist and LliboutryBenoist and Lliboutry (1978) have shown by numerical simulation that the shadowing function does not depend on the auto-correlation function of the studied profile.