Introduction
Ice cores from the mid-latitudes provide an extended record of the Earth’s climate in a densely inhabited part of the globe where instrumental records are short and other proxy records sparse. Records from the Himalaya and Tibetan Plateau are of special interest for the information they contain about the variability of the Asian monsoon.
Previous studies have demonstrated that there is a significant difference in the isotopic composition (δ18O, δD, deuterium excess) of precipitation across the Tibetan Plateau (Reference Araguás-Araguás, Froelich and RozanskiAraguás-Araguás and others, 1998; Reference Tian, Masson-Delmotte, Stievenard, Yao and JouzelTian and others, 2001, Reference Tian2003). This difference has been used to infer that precipitation in northern regions of the Plateau originates from continental moisture sources, whereas in southern regions it is primarily controlled by the strength of the Asian monsoon. Herein we present an ice-core accumulation record from East Rongbuk Col on Qomolangma (Mount Everest), Himalaya, that bears century-scale similarities to records from the Puruogangri ice cap in the central Tibetan Plateau and from Dunde and Guliya ice caps on the northeastern and northwestern margin of the Plateau, respectively. These similarities suggest that, despite the isotopic variations, there may be a common overarching mechanism controlling accumulation across the Plateau.
The 108 m ice core studied was retrieved from East Rongbuk Col (28.03° N, 86.96° E; 6518 m a.s.l.) on the northeast ridge of Qomolangma in 2002 (Reference KaspariKaspari and others, 2007) (Fig. 1). Each core segment was weighed and the density determined to within ±5%, assuming a constant core diameter. A density–depth profile was constructed and fitted with a polynomial. The ice-equivalent thickness of each annual layer was determined from this function. Henceforth all depths mentioned will be ice equivalent. The ice-equivalent length of the core was 96.7 m.
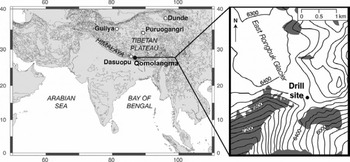
Fig. 1. Location of the 2002 Qomolangma drill site in East Rongbuk Col (solid black circle), and of other ice-core sites mentioned in the text (open circles). In the panel on the right, black lines are 500 m contours, white areas are snow and ice, and gray areas are rock.
The core was melted into 3123 samples, each of which was analyzed for soluble ions (Na+, K+, Mg2+, Ca2+, Cl−, NO3 −, SO4 2−) using ion chromatography, hydrogen isotopes (dD) using mass spectrometry, and 32 trace elements using inductively coupled plasma mass spectrometry (Reference Osterberg, Handley, Sneed, Mayewski and KreutzOsterberg and others, 2006). Strong monsoon activity during the summer results in more depleted heavy isotopes (more negative δD), and is commonly referred to as the amount effect (Reference Tian, Masson-Delmotte, Stievenard, Yao and JouzelTian and others, 2001, Reference Tian2003). Dust source elements (e.g. Ca, Al, Fe, Ti) in this region peak during the winter and spring due to unstable atmospheric conditions and strong winds. Owing to the relatively high accumulation rate (0.52 m a−1), seasonal variations in δD, soluble ions and trace elements are well preserved in the core, and were used to date ice in the core by counting annual layers. We found that ice at a depth of 86.84 m was deposited in AD 1534 ± 5 years (Fig. 2). The timescale was verified by using the first high-resolution measurements of bismuth (Bi) on an Asian ice core to identify major volcanic horizons, including Pinatubo, Agung and Tambora (Reference KaspariKaspari and others, 2007). Dating uncertainties are estimated to be ±0 years at 1963 (20 samples per year) based on a volcanic Bi horizon from the Agung (Indonesia) eruption, and ±5 years at 1534 (4 samples per year).

Fig. 2. Example of high-resolution multi-parameter dating of the Qomolangma ice core. Al, Cl−, Ca2+ and SD for the periods AD 1650–60, 1820–30 and 1980–90 are shown. SD is more negative during the summer monsoon season, and dust species (e.g. Ca2+, Al) peak in the winter/spring.
The resulting timescale provides, among other things, a record of the present thicknesses of annual layers (the thickness of ice between two annual timelines). To recover accumulation rates from this record, we need to estimate the amount by which the layers were thinned by layer-parallel extending strain as they became buried. We first describe a numerical model used to estimate the amount of thinning that has occurred, and thus recover the original layer thickness. We then compare the East Rongbuk Col accumulation-rate history with others in the region (Reference Thompson, Yao, Mosley-Thompson, Davis, Henderson and LinThompson and others, 2000, Reference Thompson2006; Reference Davis, Thompson, Cecil, Green and ThompsonDavis and Thompson, 2004; Reference Yao, Yang, Cecil, Green and ThompsonYao and Yang, 2004), and examine factors that may have contributed to differences between them.
Flow Model
Analytical approach
We approximate East Rongbuk Col as a (mathematical) saddle (Fig. 1), and consider the variation in vertical velocity with depth beneath such a saddle. The temperature at the bed was –8.9°C (Reference HouHou and others, 2004), so there is no significant slip there. We use a coordinate system with the origin at the surface in the middle of the saddle. The x and y axes are aligned with the axes of the saddle, with x parallel to the principal direction of flow away from the saddle; the z axis is vertical and pointing downward. Along the x and y axes, the strain rates ![]() and
and ![]() vanish. Ice flows symmetrically toward or away from the origin, so the velocities u and v in the x and y directions, respectively, reach a symmetrical minimum (of 0) at the origin. Thus, the strain rates
vanish. Ice flows symmetrically toward or away from the origin, so the velocities u and v in the x and y directions, respectively, reach a symmetrical minimum (of 0) at the origin. Thus, the strain rates ![]() ,
,![]() ,
,![]() and
and ![]() also vanish, and the effective shear strain rate,
also vanish, and the effective shear strain rate,![]() , becomes:
, becomes:
Continuity requires that
In addition, in the steady state ![]() , where
, where ![]() is the depth-averaged vertical strain rate, w
s is the vertical velocity at the surface,
is the depth-averaged vertical strain rate, w
s is the vertical velocity at the surface, ![]() is the ice-equivalent accumulation rate and H is the glacier thickness. Thus, there is a tendency for the geometry of the glacier surface to adjust to yield the values of
is the ice-equivalent accumulation rate and H is the glacier thickness. Thus, there is a tendency for the geometry of the glacier surface to adjust to yield the values of ![]() and
and ![]() that will, in turn, yield values of
that will, in turn, yield values of ![]() and H that balance
and H that balance ![]() . For example, an increase in
. For example, an increase in ![]() leads to an increase in H and hence surface slope. This, in turn, increases
leads to an increase in H and hence surface slope. This, in turn, increases ![]() and hence
and hence ![]() until
until ![]() .
.
Because slip at the bed is negligible while both u and v are non-zero above the bed for all x,y> 0, ![]() and
and ![]() must decrease with depth. Here we take extension as positive, following the normal convention. Along the y axis, ice surface slopes are towards the origin from both directions so
must decrease with depth. Here we take extension as positive, following the normal convention. Along the y axis, ice surface slopes are towards the origin from both directions so ![]() will be compressive or negative. Because the site is in an accumulation area, we may assume that
will be compressive or negative. Because the site is in an accumulation area, we may assume that ![]() is compressive throughout the ice column, so
is compressive throughout the ice column, so ![]() everywhere. Thus,
everywhere. Thus, ![]() must decrease with depth by Equation (2). As
must decrease with depth by Equation (2). As

any change in ![]() with depth leads to a non-linear decrease in the vertical velocity w, with depth (Reference RaymondRaymond, 1983).
with depth leads to a non-linear decrease in the vertical velocity w, with depth (Reference RaymondRaymond, 1983).
The variation in w with depth cannot be determined analytically because the stresses are not known well enough, and because the value of ![]() is needed to calculate
is needed to calculate ![]() . However, using numerical modeling, Reference RaymondRaymond (1983, equation (14)) showed that the variation with depth beneath a two-dimensional divide in an isothermal ice sheet is well described by
. However, using numerical modeling, Reference RaymondRaymond (1983, equation (14)) showed that the variation with depth beneath a two-dimensional divide in an isothermal ice sheet is well described by
with m = 2. If, alternatively, ![]() were independent of depth, the decrease in w would be linear and m = 1.
were independent of depth, the decrease in w would be linear and m = 1.
The age of the ice can be determined as a function of depth by integrating:
Carrying out the integration, using Equation (4) for w, yields


A least-squares fit of Equation (6a) (see Appendix (1)) to our measured age–depth profile yields m = 1.11 and w
s = 0.49 m a−1(Fig. 3). The rleatively low value of m suggests that ![]() is nearly constant over much of the depth, and that most of the decrease in velocity occurs near the bed.
is nearly constant over much of the depth, and that most of the decrease in velocity occurs near the bed.

Fig. 3. Measured age–depth profile compared with profiles calculated using Equation (6a) with m = 1.01, 1.11 and 1.21 and w s = 0.49 m a−1. Also shown is the profile calculated with m = 1.3 and w s = 0.68 m a−1, the solution from the equation used by Reference Davis, Thompson, Yao and WangDavis and others (2005). Breaks in slope in the observed time–depth curve are marked by +.
The low value of m could reflect the presence of warmer ice near the bed, the location of the hole some distance from the true divide, or the three-dimensional nature of the col. We used Equation (4), a temperature-dependent form of the flow law and the measured temperature gradient, −0.008 K m−1,between 15 and 96 m in the borehole to study the effect of temperature, and found that the softening effect of warmer temperatures near the bed could account for only a small part of the difference. Similarly, Raymond’s two-dimensional numerical results for locations greater than one ice thickness away from the divide are well approximated by Equation (4) with m ≈ 1.4, so our appreciably lower value is not consistent with his modeling. We thus suspect that the three-dimensional geometry of the col is likely to be responsible for most of the difference.
However, it is clear from Figure 3 that there are systematic differences between the model and the measured profiles, such that the accumulation rate appears to have been higher recently and lower when the ice between 33 and 49 m was deposited. To study these further, we note that breaks in slope, marked by crosses in Figure 3 and clearly visible in enlarged versions of the figure, occur at about AD 1935, 1835, 1720 and 1620. We thus wrote Equation (6a) in the form

and, using m = 1.11, obtained least-squares fits to the curve segments between these pairs of dates. For the fit to the segment between 1935 and 2000 we specified a = 0. The resulting values of w s are shown in Table 1.
Table 1. Accumulation rates (m a−1) during time intervals (AD) for the values of m shown in the lefthand column

A Numerical Model
To further analyze the systematic departures of Equation (6a) from our age–depth profile based on layer counting, we developed a numerical model. This model simulates growth of the glacier from zero thickness.
In a previous study, Hou and others (Reference Hou2004) measured CH4 and 18Oatm profiles in the ice core used in this study and also in a slightly longer core collected from East Rongbuk Col a year earlier, in 2001. They compared the CH4 and δ18Oatm signatures in the East Rongbuk Col cores with those in the GRIP and GISP2 cores, two >3000 m cores from central Greenland. They estimated that ice 0.6–0.9 m above the bed in the 2002 East Rongbuk Col core, and 0.05–1.8 m above the bed in the 2001 core, dated to between 50 BC and AD 500.
To provide spin-up time for the model, we assumed that the col was free of snow 4000 years ago, and began our integration then. (A sensitivity study, discussed below, shows that this assumption has no significant effect on our results.) We then allowed ice to accumulate at a rate ![]() and to flow away at a rate that resulted in thinning.
and to flow away at a rate that resulted in thinning.
To determine the rate of thinning, we note that when ice is frozen to the bed, laminar flow theory gives a depth-averaged velocity, ū, of

where α is the slope of the glacier surface, S f is a shape factor, ρ is the density of ice and g is the acceleration due to gravity (Nye, Reference Nye1952; Hooke, Reference Hooke2005, p.87). Neglecting the small change in H as we move away from the divide, and taking the derivative of ū with respect to x, gives

and similarly for ![]() . Over a short distance from the divide, noting that α = 0 at the divide, we can approximate
. Over a short distance from the divide, noting that α = 0 at the divide, we can approximate ![]() by α
Δx
/2, where α
Δx
is the slope at x = Δx. Then dα/dx is α
Δx
/Δx, and Equation (8) becomes
by α
Δx
/2, where α
Δx
is the slope at x = Δx. Then dα/dx is α
Δx
/Δx, and Equation (8) becomes

A similar relation would apply for ![]() Thus, using Equation (2) we assume that
Thus, using Equation (2) we assume that
where α Δ is a measure of the excess of the (positive) longitudinal slope over the (negative) transverse slope in the col and the constant of proportionality (with n = 3) is
As ![]() , we then have
, we then have

The vertical velocity at any depth is then calculated from Equation (4) with m = 1.11.
To run the model, one first enters the accumulation rate as a function of time and guesses a value of S f α Δ. In the initial year, 2000 BC, a layer of ice is deposited on the bedrock and a new ice thickness is calculated, as is w s from Equation (12). For the first layer, this w s is simply subtracted from the thickness and the new z coordinate of the top of the layer is saved. Another layer of ice is then added. For this and subsequent layers, Equations (4) and (12) are used to determine w at the level of each previously deposited layer, and the elevation of each such layer is adjusted accordingly. At the end of 4000 years of accumulation, the ice thickness is compared with the measured value of 96.7 m and the value of S f α Δ is adjusted accordingly. Once the calculated and measured thicknesses are in agreement, within 0.05 m when S f α Δ is specified to five decimal places, the resulting age–depth profile is compared with the measured one.
For the initial run of the model, we used the accumulation history from the above least-squares analysis (Table 1, row 2) with m = 1.11. For the period prior to that covered by the layer-counting data, we used the weighted mean of the other accumulation rates (Table 1). The agreement with the measured profile is quite good, though the calculated curve falls slightly below the observed one (Fig. 4). This is probably because the least-squares fits tend to give too much weight to transitional regions in the vicinity of the break points. By making small adjustments in the accumulation pattern and seeking new values of S f α Δ that gave a satisfactory agreement with the measured thickness, we were able to obtain a significantly better fit (Fig. 4). The resulting accumulation rates are shown in the third row of Table 1. In the basal ice, where we did not have layer-counting data to constrain the accumulation rate, we again used the weighted mean of the other values.

Fig. 4. Output of the numerical model. (b) is an enlargement of the area in the dashed box in (a). Of the three time–depth curves, the thick gray curve is based on our layer counting and the two black curves are from our numerical model. The dashed black curve uses the accumulation rates determined by least squares, and the solid black curve uses accumulation rates, obtained by trial and error, that better match the observed curve. Breaks in slope in the observed time–depth curve are marked by +. (Use the top and left axes for normalized layer thickness and the bottom and right axes for ice thickness.)
The model dates for the basal ice in our core are AD 776 at 0.6 m above the bed and AD 900 at 0.9 m. These ages are 300–400 years younger than the younger limit (AD 500) estimated by Hou and others (Reference Hou2004), but are within the uncertainty in their approach.
Also shown in Figure 4 is the ice thickness as a function of time. The glacier reached a thickness of 94.467 m i.e. (ice equivalent) after 542 years of integration starting at 2000 BC (not shown) and, owing to the constant accumulation rate assumed, maintained this thickness until AD 1535 when we changed the accumulation rate. Thereafter, it asymptotically approached a new equilibrium thickness some years after each change in accumulation rate. According to the model, the first 542 years of accumulation is represented, today, by the basal 3 mm of ice, and the first 2000 years by the basal 67 mm.
Lastly, we divided the final thickness of each ice layer by its original thickness to illustrate, in Figure 4, the vertical shortening experienced by each layer as a function of depth.
To investigate the effect of the initial condition (no ice at 2000 BC) on the results, we also ran a model starting at 500 BC. With the same accumulation pattern and values of m and α Δ used previously, results were essentially identical to those in Figure 4, to within ∼±0.0002, from AD 700 to the present. Thus, our initial condition that the col was ice-free 4000 years ago appears to have no effect on the final results.
As a sensitivity test, we also ran the model with m = 1.01 and 1.21 (Fig. 3). To match the observed accumulation pattern, we then had to alter the accumulation rate by a few centimeters per year near the top of the core and a few decimeters per year near the bottom (Table 1). The year AD 1535 is at a depth of 86.56 m in our reference model (m = 1.11). With m = 1.01 and 1.21 m, the year AD 1535 occurs 0.63 m higher and 0.14 m lower, respectively.
Accumulation-Rate History
To study variations in accumulation rate from year to year, we divided the measured thickness of each layer by the normalized layer thickness at the appropriate depth (Fig. 5). As already anticipated from the above results (Table 1), the accumulation rate decreases from AD 1534 to ∼1880, and then increases until ∼1970 (Fig.5). In the following 30 years, it decreases again. The decreasing trend in accumulation since ∼AD 1534 is consistent with the Cl− and Ca2+ record from this core; Cl− (from marine sources) has decreased and Ca2+ (from continental sources) has increased since ∼AD 1400, suggesting a decrease in northward incursions of the summer South Asian monsoon (Kaspari and others, Reference Kaspari2007).

Fig. 5. Reconstructed Tibetan Plateau precipitation record from tree rings (Reference Wu, Bradley and JonesWu, 1995) and ice-core accumulation-rate time series from Dunde (Reference Davis, Thompson, Cecil, Green and ThompsonDavis and Thompson 2004), Guliya (Reference Yao, Yang, Cecil, Green and ThompsonYao and Yang, 2004), Puruogangri (Reference ThompsonThompson and others, 2006), East Rongbuk Col (Reference KaspariKaspari and others, 2007; this work) and Dasuopu (Reference Thompson, Yao, Mosley-Thompson, Davis, Henderson and LinThompson and others, 2000). The horizontal line through each time series is the average, and the gray shaded regions denote below-average accumulation.
Errors in picking boundaries between annual layers are unlikely to be responsible for these century-scale trends. Missing an annual layer would result in an apparent doubling of the accumulation rate for that year, and conversely. Few such anomalies are observed in the dating, and such errors would have little effect on the long-term averages. However, the dating uncertainty increases with depth in the core. Thus it is possible that the higher accumulation rates, particularly prior to AD 1600, could be, in part, an artifact of having missed some annual layers. Consequently, in the following discussion we focus primarily on the record since AD 1600.
On a multi-decadal timescale, the variations in climate that are most likely to affect the accumulation rate are changes in temperature and atmospheric circulation that alter the amount and pattern of precipitation. Increased concentrations of greenhouse gases, for example, are projected to result in warming of the Indian Ocean, an increase in precipitation in the region affected by the Asian monsoon and a change in Asian monsoon circulation (e.g. Ueda and others, Reference Ueda, Iwai, Kuwako and Hori2006; Kripalani and others, Reference Kripalani, Oh, Kulkarni, Sabade and Chaudhari2007). Rain-gauge data indicate that the amount of monsoon rainfall in India has remained fairly stable since 1871 (Parthasarathy and others, Reference Parthasarathy, Munot and Kothawale1995); however, there has been a trend toward an increase in frequency and magnitude of extreme events in central India since the 1950s. This trend is associated with warmer summer sea surface temperatures (Goswami and others, Reference Goswami, Venugopal, Sengupta, Madhusoodanan and Xavier2006).
Thus, the 20th-century increase in accumulation in East Rongbuk Col could be associated with recent changes in monsoon dynamics. If this is the case, a similar accumulation increase would be expected in other Asian ice cores that are strongly influenced by the monsoon. However, regional differences in accumulation patterns may occur due to variations in atmospheric circulation, and hence precipitation patterns.
Comparison with Other Asian Ice-Core Accumulation-Rate Histories
Our accumulation-rate time series is broadly similar to those derived from four other ice cores from the Tibetan Plateau (Fig. 5). Before discussing this in detail, however, we consider the extent to which differences in the method of analysis may have affected the results.
In previous studies of accumulation rates using Asian ice cores (Thompson and others, Reference Thompson1989, Reference Thompson, Yao, Mosley-Thompson, Davis, Henderson and Lin2000; Reference Yao, Yang, Cecil, Green and ThompsonYao and Yang, 2004; Davis and others, Reference Davis, Thompson, Yao and Wang2005), the authors have fitted a function, of the form
to observed layer-thickness data and then calculated the original thickness of each layer by comparing the calculated with the observed thickness. Here, λ(z) is the layer thickness as a function of depth, z; λ0 is the layer thickness at z = 0 (the ice-equivalent accumulation rate) and p is a fitting parameter. The papers by Thompson and others (Reference Thompson1989, Reference Thompson, Yao, Mosley-Thompson, Davis, Henderson and Lin2000) and by Davis and others (Reference Davis, Thompson, Yao and Wang2005) attribute Equation (13) to Bolzan (Reference Bolzan1985); although it does not appear in his paper, it can be derived from equations appearing there (see Appendix (2)). Equation (13) is very similar to our Equation (4), but layer thicknesses are substituted for w and w s. These substitutions are logical: in a steady state, w s = λ0, and, at depth z, vertical velocity, w(z), must be sufficient to move the top of layer λ(z) down one layer thickness in a year. Based on comparison of Equations (4) and (13), it is clear that p = m – 1.
Davis and others (Reference Davis, Thompson, Yao and Wang2005, equation (2)) point out that Equation (13) can be solved for p and w s if annual layers at two different depths can be dated accurately (see Appendix (3)). However, when we do this for the respective segments of our age–depth curves between successive break points, we get values of m that range from 0.7 to 2.9. As m should not vary significantly with time unless the divide has moved several ice thicknesses, and as m < 1 is physically unrealistic (see Appendix (4)), this approach is not suitable in our case. Furthermore, if we solve for p and w s using dated layers at the top and bottom of the core, the values obtained, p = 0.3 (m = 1.3) and w s = 0.68 m a−1,yield an age–depth profile (Fig. 3) that is in quite poor agreement with the observed profile.
Were we to have used only Equation (13) in our modeling, we would have ignored the obvious breaks in slope in the curve of age versus depth obtained from layer counting (Figs 3 and 4). For example, if we calculate layer thicknesses from Equation (13) and the values of m and w s (1.11 and 0.46 m a−1,respectively) from our least-squares fit to obtain p (= m – 1) and λ0 (= w s) (see Appendix (5)), the resulting accumulation rates from AD 1550 to 1900 are systematically 0.1–0.2 m a−1 higher than those in Figure 5, with differences being greatest during years with the highest accumulation rates (Fig. 6). However, the long-term trends are the same.

Fig. 6. Accumulation rate for the East Rongbuk Col ice core calculated with the numerical model (solid line) and with Equation (13) (dashed line), and the difference between the two.
Lacking the original layer-thickness data and information on how Equation (13) was implemented (least-squares or a two-point approximation) for the other sites, we cannot assess the extent to which accumulation rates calculated using Equation (13) would differ from those obtained from our numerical model. For example, if age–depth profiles like Figure 3 for the other sites did not have any breaks in slope and if a least-squares approach was used to obtain p, the approaches would be essentially identical. However, the prolonged periods during which accumulation deviates systematically from the mean in the other records (Fig. 5) suggest that age–depth profiles for these sites would contain breaks in slope.
As noted, our accumulation-rate time series is similar to those from Guliya (6200 m a.s.l.) (Reference Yao, Yang, Cecil, Green and ThompsonYao and Yang, 2004) and Dunde (5325 m a.s.l.) (Thompson and others, Reference Thompson1989) ice caps on the northern edge of the Tibetan Plateau and from Puruogangri ice field (5970 m a.s.l.) (Thompson and others, Reference Thompson2006) at the western end of the Tanggula range, ∼700 km north-northeast of Qomolangma (Figs 1 and 5), inasmuch as all show a gradual decline over two to three centuries, followed by an increase starting in the late 1800s to early 1900s and then a decline in the late 1900s. The significance of this correspondence is not clear, however, given the potential for substantial differences in moisture source and transport between the Himalaya and the northern Tibetan Plateau. Our time series is most similar to a precipitation record derived from a composite tree-ring record (Reference Wu, Bradley and JonesWu, 1995) from lower elevations (3000–4000 m) on the Plateau (Fig. 5). As this record is from sites scattered over the Plateau, it may imply that, despite the potential differences in moisture transport, correspondence between the several records from the northern part of the Plateau and that from East Rongbuk Col is more than coincidental.
Paradoxically, the period of rising accumulation rates broadly coincides with a period of retreat of glaciers worldwide, including those in the Himalaya (e.g. Mayewski and Jeschke, Reference Mayewski and Jeschke1979; Reference Yao, Wang, Liu, Pu and LuYao and others, 2004). This retreat in the Himalaya, particularly in the late 1800s and early 1900s, may be a response to past changes in climate, including lower accumulation during the 1800s, and/or warming following the cooler Little Ice Age. However, the continuing recent retreat of many glaciers in the Himalaya and on the Tibetan Plateau, during a time when accumulation rates have increased, suggests that glaciers now are responding more to temperature than to accumulation. This is consistent with the conclusion reached by Thompson and others (Reference Thompson2006) that glacier retreat in the tropics and subtropics is caused by rising air temperature rather than reduced precipitation.
However, on Dasuopu glacier (7200 m a.s.l.), 125 km northwest of Qomolangma, accumulation appears to have been highest between 1800 and 1880 (Thompson and others, Reference Thompson, Yao, Mosley-Thompson, Davis, Henderson and Lin2000), a period during which it was relatively low elsewhere. Given that the Dasuopu record is that closest to East Rongbuk Col, this difference is puzzling. Previous authors have suggested that variations in snow accumulation at Dasuopu are related to the intensity of the Asian monsoon (Thompson and others, Reference Thompson, Yao, Mosley-Thompson, Davis, Henderson and Lin2000; Reference Davis, Thompson, Cecil, Green and ThompsonDavis and Thompson, 2004; Duan and others, Reference Duan, Yao and Thompson2006), the regional Hadley circulation (Zhao and Moore, Reference Zhao and Moore2002) or weakening of the Pacific trade winds (Zhao and Moore, Reference Zhao and Moore2006). If ice-core accumulation-rate time series are representative of large-scale atmospheric circulation processes such as these, one would not expect such large differences between the Dasuopu and East Rongbuk Col records. It seems unlikely that uncertainties related to the application of Equation (13) could explain so pronounced a difference. Other factors that could contribute to such differences include:
Different moisture trajectories
The majority of precipitation in the Himalaya is deposited between June and September, during the summer monsoon. In the western Himalaya, moisture comes directly from the Arabian Sea (Fig. 1), while in the east it is transported from the Arabian Sea across southern India to the Bay of Bengal, and thence northward along the Brahmaputra river valley (Reference Lin and WuLin and Wu, 1990; Reference Shrestha, Wake, Dibb and MayewskiShrestha and others, 2000). Reference Davis, Thompson, Cecil, Green and ThompsonDavis and Thompson (2004) suggest that Dasuopu is located close to the dividing point between these two moisture regimes. Thus, Dasuopu may be more heavily influenced by the western moisture regime, and East Rongbuk Col by the eastern one. However, the East Rongbuk Col annual accumulation rate since 1871 is significantly correlated with the all-India Precipitation (Parthasarathy and others, Reference Parthasarathy, Munot and Kothawale1995) in regions of northwest India (n = 131, p < 0.005; western Uttar Pradesh (r = 0.22), Haryana, Chandigarh and Delhi (r = 0.26) and Punjab (r = 0.24)), suggesting that the western moisture regime may, indeed, be an important control on East Rongbuk Col accumulation.
Moisture associated with the westerlies during non-monsoon periods could contribute to the differences between the two records. Although winter deposition has been thought to make only a small contribution to the net budget in the Himalaya, recent research suggests that winter precipitation events may account for a substantial amount of the annual precipitation at Dasuopu (Tian and others, Reference Tian, Yao, White, Yu and Wang2005), and increased early winter snowfall was identified as a possible cause for the higher accumulation at Dasuopu during the 1800s (Davis and others, Reference Davis, Thompson, Yao and Wang2005). The Dasuopu drill site (7200 m a.s.l.) is higher than the East Rongbuk Col site (6518 m a.s.l.), and the mean accumulation from AD 1534 to 1997 is greater at Dasuopu (0.80 m for core 2; 0.99 m for core 3) than at East Rongbuk Col (0.52 m). The higher accumulation at Dasuopu may be caused by larger contributions of winter snow deposition from the westerlies at higher elevations, and could account for the differences in the Dasuopu and East Rongbuk Col records. In this case, the accumulation record from East Rongbuk Col may be a better proxy for summer monsoon variability, and that from Dasuopu for winter snow deposition from westerly sources.
Complex mountain meteorology
The large vertical relief and complicated topography in the Himalaya influence the distribution of precipitation through localized storms, strong orographic effects and drifting. Previous studies of the spatial variability of precipitation in Nepal (Sankar-Rao and others, Reference Sankar-Rao, Lau and Yang1996) and India (Parthasarathy and others, Reference Parthasarathy, Munot and Kothawale1995; Goswami and others, Reference Goswami, Venugopal, Sengupta, Madhusoodanan and Xavier2006) demonstrated that precipitation may be highly variable over short distances. For example, the accumulation-rate time series from two ice cores drilled 100 m apart at Dasuopu show similar long-term trends, but on shorter timescales there are systematic differences between the two records (Thompson and others, Reference Thompson, Yao, Mosley-Thompson, Davis, Henderson and Lin2000) (Fig. 5, Dasuopu cores 2 and 3).
If non-monsoon westerly sources are insignificant at both East Rongbuk Col and Dasuopu, so accumulation at both is controlled by monsoon moisture sources, the differences between them during the 19th century would require systematic changes in opposite directions lasting several decades. This would suggest a long-term change in microclimate, such as might be brought about by a subtle but persistent regional shift in wind direction and/or speed that altered local storm tracks or drifting patterns.
Lastly, the Dasuopu drill site is ∼700 m higher than East Rongbuk Col, and is located closer to the subtropical jet stream. Thus Dasuopu is likely to be more sensitive to variations in the strength and position of the jet stream.
Ice-flow dynamics
Under appropriate circumstances, basal ice at a core site may have originated in a location with a different accumulation regime, and this could be responsible for an apparent long-term change in accumulation. However, the East Rongbuk Col record and the two Dasuopu records are from cores taken in cols, and the Dunde and Puruogangri records are from ‘summits’ or domes. In none of these cases would we expect any significant flow to have taken place in the last 500 years.
The Guliya core is from 6200 m a.s.l. in a broad cirque-like basin (Reference Yao, Yang, Cecil, Green and ThompsonYao and Yang, 2004). The basin is fed by much thinner ice from as high as 6700 m to the north. The ice is cold-based, so no sliding is expected. The flowline is ∼8000 m long, mean accumulation rate is ∼0.2 m a−1 and the ice is ∼300 m thick, so the balance velocity at the core site would be ∼5 m a−1. Thus, ice may have moved 2 km in 400 years. Given the topography, it does not appear that this would change the accumulation rate substantially, but subtle changes due to drifting are possible.
Inaccuracies in identifying annual layers
Misidentification of annual layers could result in calculated accumulation rates that differ from the actual ones. Difficulty in correctly identifying annual layers can occur when the seasonal signal is ambiguous, or at depth in an ice core when the sampling resolution decreases due to layer thinning. However, to explain the more than doubling of the accumulation rate between the late 19th century and the mid-20th century in the East Rongbuk Col core in this way would mean that we missed more than 60 layers in the last 60 years. This is extremely unlikely.
In conclusion, we suspect that differences in moisture trajectories and the vagaries of mountain meteorology are the most likely causes for the different accumulation-rate histories at Dasuopu and East Rongbuk Col.
Conclusions
We have developed a numerical model to refine the calculation of annual accumulation rates from annual-layer thickness data and applied it to an ice core from East Rongbuk Col. Our model suggests that the accumulation rate at East Rongbuk Col decreased from AD 1534 to ∼1880. This is consistent with a reduction in northward incursions of the summer south Asian monsoon inferred from geochemical evidence from the same ice core (Kaspari and others, Reference Kaspari2007).
The model further suggests an increase in accumulation rate in the 20th century. This may be related to enhanced monsoon precipitation associated with a change in monsoon dynamics. At sites further north on the Tibetan Plateau, the accumulation rate doubles during this time period, whereas on East Rongbuk Col it increases by a factor of ∼4.5, possibly indicating that the former are not as strongly influenced by the monsoon.
On centennial timescales, the East Rongbuk Col accumulation-rate record is in broad agreement with other paleo-climate records from the Tibetan Plateau including those from Guliya (Reference Yao, Yang, Cecil, Green and ThompsonYao and Yang, 2004) and Dunde (Reference Davis, Thompson, Cecil, Green and ThompsonDavis and Thompson, 2004) ice caps, from the Puruogangri ice field (Thompson and others, Reference Thompson2006) and from tree-ring records (Reference Wu, Bradley and JonesWu, 1995). These records all show a gradual decrease in accumulation (or precipitation) over two to three centuries, followed by an increase starting in the late 1800s to early 1900s and finally a decrease in the late 1900s. The similarity between these records suggests that there may be an overarching mechanism controlling precipitation over the Himalaya and Tibetan Plateau.
Paradoxically, accumulation-rate trends on nearby Dasuopu glacier differ substantially from the East Rongbuk Col and other Asian records. The factors that are most likely to contribute to this discrepancy are differences in moisture trajectories and complex mountain meteorology. The Dasuopu site is at a higher elevation than the other sites, and may be more affected by variations in the jet stream and/or receive larger contributions of precipitation from winter westerly moisture sources. This is consistent with the higher mean accumulation rate at Dasuopu relative to the East Rongbuk Col. Alternatively, or in addition, subtle changes in wind direction and/or speed may have altered drifting patterns.
The dissimilarity between the Dasuopu and other Asian paleoclimate records highlights the need for caution when using single records to reconstruct past variations in large-scale atmospheric circulation, such as the strength of the monsoon or of Hadley circulation. However, when combined, these records can be used to refine our understanding of moisture transport and climate variability in the Himalaya and across the Tibetan Plateau.
Finally, the inconsistencies uncovered by our analysis of the East Rongbuk Col core using Equation (13) suggest the need for caution in applications of this equation.
Acknowledgements
This research was funded by the US National Science Foundation (NSF ATM 0139491), the US National Oceanic and Atmospheric Administration (NOAA(NA05OAR4311109)), the Natural Science Foundation of China (90411003, 40401054) and the Chinese Academy of Sciences (‘Talents Project’ and the Innovation Programs: KZCX3-SW-339/344). We thank C.F. Raymond for reviewing an early version of the modeling discussion, and B. Hanson and J. Walder for insightful reviews.
Appendix
1. To obtain the least-squares solution we first specified values of m and w s and calculated

where t c and t o are the times of deposition calculated from Equation (6a) and obtained from the layer counting, respectively, and n is the total number of layers identified (465). We then incremented either m or w s and repeated the calculation. The procedure was implemented in Fortran. During each run of the program, 400 pairs of values of m and w s were tested. The starting values and increment were varied between runs to narrow down the interval within which the minimum S occurred. The final increment was 0.01 for both m and w s. The values that yielded the minimum S were m = 1.11 and w s = 0.49.
2. To obtain Equation (13) from Reference BolzanBolzan (1985), integrate our Equation (3) using his equation (7) for ![]() , and use the arguments in the paragraph containing Equation (13) to justify substituting λ(0) for his
, and use the arguments in the paragraph containing Equation (13) to justify substituting λ(0) for his ![]() and λ(z) for w(z).
and λ(z) for w(z).
3. To solve Equation (13) for p and w s using two known pairs of z and t, note the congruence between Equations (13) and (4) and use Equation (4) in Equation (5) to obtain Equation (6). Then substitute the known values of z and t in Equation (6) to get two equations in w s and m, and solve for these two unknowns. The resulting equation, given by Davis and Thompson (2005, equation (2)) but not derived by them, is:

where p = m – 1 and t 1, z 1, t 2 and z 2 are the known values. Inserting the known values, this can be reduced to:
where Ai = [H/(H – zi )], and B = t 1/t 2. Clearly, p = 0 is a trivial solution of no interest. The other solution for p must be obtained by trial and error, which is relatively simple using a spreadsheet. Equation (6) can then be used to obtain w s, thus:

Note that z = 0, t = 0 cannot be used as one of the pairs of known values, as one of the values of Ai then becomes 1 and B is either 0 or infinite. It is also important to note that if one of the known values of zi is at a relatively shallow depth and the corresponding ti is thus small, w s → z 1/t 1; in other words, w s approaches the accumulation rate. This can be seen by expanding the term in inner brackets in Equation (A3) in a Maclaurin series:

When p ≪ 1 and z 1 ≪ H, the second term on the right is negligible compared with the first term.
4. Values of m < 1 imply that ![]() increases with depth. This would require that the horizontal velocity increase with depth, which is highly unlikely in this situation.
increases with depth. This would require that the horizontal velocity increase with depth, which is highly unlikely in this situation.
5. To calculate layer thicknesses using Equation (13), we rearranged Equation (6a) to obtain

and solved this for integer values of t. We then obtained the accumulation rate for each year, ti , from
where zi and zi +1 are the depths to the top and bottom of the layer deposited between times ti and ti +1, calculated from Equation (A3), and Δzi is the measured thickness of ice between these two times measured in the core.









