1. Introduction
Since variations in stable oxygen isotopic compositions (δ18O) are a good indicator of past surrounding environments, these have been used for climate research (Reference HoefsHoefs, 2009). For example, the vertical profiles of δ18O preserved in ice cores from Greenland and Antarctica have revealed a detailed temperature record for the past 700 ka from the relationship between δ18O and surface air temperature (Reference DansgaardDansgaard and others, 1993; Reference Johnsen, Clausen, Dansgaard, Gundestrup, Hammer and TauberJohnsen and others, 1995), and the geographical distribution of the δ18O values of precipitation provides implications for the hydrological cycle on a global scale (Reference Joussaume, Sadourny and JouzelJoussaume and others, 1984; Reference Koster, de Valpine and JouzelKoster and others, 1993). In the case of sea ice, δ18O has been used to reveal growth processes mainly related to snow. Since snow usually has much lower values of δ18O (∼−20% to −5%) than sea water (∼−1% to 0%), it is a useful tool for distinguishing snow ice from ice of sea-water origin and quantifying the fraction of snow (Reference Lange, Shlosser, Ackley, Wadhams and DieckmannLange and others, 1990; Reference Jeffries, Shaw, Morris, Veazey and KrouseJeffries and others, 1994, Reference Jeffries, Worby, Morris and Weeks1997; Reference Worby and MassomWorby and Massom, 1995; Reference Granskog, Leppäranta, Kawamura, Ehn and ShirasawaGranskog and others, 2004; Reference Toyota, Takatsuji, Tateyama, Naoki and OhshimaToyota and others, 2007). In addition to its relevance to snow, δ18O also holds promise as a tool for deducing columnar ice growth rate (Reference Souchez, Tison and JouzelSouchez and others, 1987, Reference Souchez, Tison and Jouzel1988; Reference Eicken and JeffriesEicken, 1998; Reference Smith, Langhorne, Frew, Vennell and HaskellSmith and others, 2012).
During the freezing of sea water, the heavier O18-bearing isotopomer of water (H2 18O) is preferentially entrapped in the sea ice. Thus sea ice takes a somewhat larger value of δ18O than the underlying sea water. The degree of fractionation depends significantly upon the freezing conditions, mainly the freezing rate, and is usually represented by a fractionation factor (α si), defined by the isotope ratio of newly formed sea ice (R ice = (18O/16O) ice) divided by that of the underlying sea water (Rwater = (18O/16O)water). For simplicity here we use an effective fractionation coefficient (εeff, si), defined by 1000 ln (α si), which is approximately equal to δ18Oice–δ18Owater. If the relationship between εeff, si and the freezing rate is derived, it is expected that the growth rate history of sea ice can be retrieved from the vertical δ18O profiles of the sea-ice core, referenced to the δ18O of the sea water from which the sea ice formed. That would allow for the estimation of the seasonal variation of ice growth rate, providing useful information on the timing and magnitude of salt fluxes to the deep ocean. Since such salt fluxes drive the global thermohaline circulation, the investigation of δ18O of sea ice can contribute to climate research in the polar region. In addition,εeff,si is a critical parameter for estimating snow contribution quantitatively (Reference Jeffries, Worby, Morris and WeeksJeffries and others, 1997; Reference Toyota, Takatsuji, Tateyama, Naoki and OhshimaToyota and others, 2007) and examining water-mass formation processes from stable-isotopic ratios in the polar oceans (Reference Macdonald, Paton, Carmack and OmstedtMacdonald and others, 1995; Reference Melling and MooreMelling and Moore, 1995; Reference Yamamoto, Tanaka and TsunogaiYamamoto and others, 2001). In the Arctic Ocean there has been an attempt to reconstruct the ocean surface δ18O field using δ18O profiles from sea-ice cores (Reference Pfirman, Haxby, Eicken, Jeffries and BauchPfirman and others, 2004).
At the interface between continuous sea-ice cover and water, the fractionation coefficient between pure water and ice has been estimated at 2.91% under equilibrium laboratory conditions (Reference Lehmann and SiegenthalerLehmann and Siegenthaler, 1991). More widely varying values have been reported from observations at sea under varying freezing conditions. For example, Reference Macdonald, Paton, Carmack and OmstedtMacdonald and others (1995) estimated a fractionation coefficient of 2.57 ± 0.10‰ at slow growth rates in spring for ∼2 m thick ice. They studied the offset of δ18O between the bottom of the sea ice and the underlying water in the Canadian Beaufort Sea. Reference Melling and MooreMelling and Moore (1995) found a fractionation coefficient of 2.09 ± 0.38‰ for ∼1 m thick ice in nearly the same season and region. From wintertime observations, Reference Toyota, Takatsuji, Tateyama, Naoki and OhshimaToyota and others (2007) made a statistical estimate of the average εeff, si of 1.73 ± 0.23‰ from the difference in the δ18O distribution between sea ice (granular ice) and sea water for 0.1–2.5 m thick sea ice from the Sea of Okhotsk. Slightly higher values (1.91 ± 0.30‰) were obtained using a similar method for 0.6–2.4 m thick sea ice from the Weddell Sea, Antarctica (Reference Toyota, Haas, Nicolaus, Li and AokiToyota and others, 2008). Thus the range of εeff, si is ∼1‰ depending on the freezing rate. It is therefore important to correlate εeff, si with ice growth rates.
Since during sea-ice formation brine is partly entrapped in the sea ice and the expelled highly saline water induces convection underneath sea ice during freezing, the experimental results on the εeff, si–growth-rate relationship obtained with pure water and ice by Reference Lehmann and SiegenthalerLehmann and Siegenthaler (1991) cannot be simply applied. Although Reference Eicken and JeffriesEicken (1998) theoretically derived the formula that predicts the sea-ice growth rate from εeff, si based on the stagnant boundary-layer model (Reference Burton, Prim and SlichterBurton and others, 1953; Reference Weeks, Lofgren and OuraWeeks and Lofgren, 1967), the parameters used in the model still need optimization from direct measurement. In this model, the key parameters are the boundary-layer thickness (zbl) and equilibrium fractionation coefficient ![]() , and Reference Eicken and JeffriesEicken (1998) assumed these parameters to be zbl = 1.3 mm and
, and Reference Eicken and JeffriesEicken (1998) assumed these parameters to be zbl = 1.3 mm and ![]() . However, these values have not yet been validated over a full range of observational data. In McMurdo Sound, Antarctica, Reference Smith, Langhorne, Frew, Vennell and HaskellSmith and others (2012) showed from in situ measurements of δ18O and measured growth rates typical of sea ice >1 m thick that the Reference Eicken and JeffriesEicken (1998) formula underestimated the real growth rate and they suggested some modification of the parameters used in Eicken’s model. However, their data contained incorporated platelet ice in addition to columnar ice.
. However, these values have not yet been validated over a full range of observational data. In McMurdo Sound, Antarctica, Reference Smith, Langhorne, Frew, Vennell and HaskellSmith and others (2012) showed from in situ measurements of δ18O and measured growth rates typical of sea ice >1 m thick that the Reference Eicken and JeffriesEicken (1998) formula underestimated the real growth rate and they suggested some modification of the parameters used in Eicken’s model. However, their data contained incorporated platelet ice in addition to columnar ice.
One of the keys to resolving this issue is to collect δ18O data for sea ice over a wide range of growth rates. In the field, a large growth rate can be achieved only for relatively thin ice, making it dangerous to collect such ice samples, while slow growth rate data can be obtained safely at a site with relatively thick ice but long-term monitoring is required. From laboratory experiments, for technical reasons it is not easy to obtain very slow growth rates. Therefore, in this study relatively large growth rates (>2.2 × 10−7 m s−1) were obtained from laboratory tank experiments, while relatively small growth rates (<2.5 × 10−7 m s−1) were provided by in situ observations in McMurdo Sound and the southern Sea of Okhotsk. By combining these datasets, a wide range of growth rates was obtained. Only data from ice of columnar crystal structure from the McMurdo Sound observations are included here to simplify the analysis by removing possible confounding influences of crystal structure. Our purpose is to examine the theoretically derived formula that correlates fractionation of δ18O with growth rate based on real data, in order to find the best-fit parameters for use in the theoretical model. In addition, an empirical formula is derived that correlates fractionation of δ18O with growth rate over a wide range of growth rates. Since this issue is closely related to the microphysics of sea ice during freezing, we believe that our study might also provide some insights into freezing processes at the interface.
2. Laboratory Experiment
2.1. Apparatus
In order to collect samples for relatively large growth rates, we conducted a laboratory experiment with a thermally insulated rectangular tank (inner dimensions of 0.3 m depth × 0.3 m width × 0.65 m height) in a cold room (Fig. 1). The tank was made from transparent acrylic 0.01 m thick and was covered on all surfaces except the upper surface with a 0.1 m thick layer of StyrofoamTM to prevent freezing on the side walls and the bottom of the tank. Natural sea water (S = 32.5 on the Practical Salinity Scale 1978 (UNESCO, 1981); δ18O = −0.8‰) collected from the Pacific Ocean near the coastal region of Hokkaido, Japan, was poured into the tank up to 0.60 m depth, and sea ice was grown to ∼5 cm thickness under calm and steady conditions. We had to stop freezing at this thickness to minimize the change in the freezing conditions caused by the expelled brine, i.e. the decrease in the freezing-point temperature due to the increase in water salinity within the tank. Growth rates were controlled by changing the room temperature from −5°C to −20°C. The temperature of the air 5 cm above the ice surface and in the ice or water at tank depths of 0.5, 2.5, 5, 15, 35 and 55 cm was monitored using copper–constantan thermocouples mounted on the side wall (Fig. 1). These temperature data were logged on a data logger (YOKOGAWA, model DR230) at 1 min intervals. Ice thickness was measured visually at (mostly) 3 hour intervals with a measuring scale attached to the side wall. In order to monitor the salinity and δ18O of sea water, we made small holes on a side wall of the tank at depths of 5, 15, 25, 35, 45 and 55 cm and fitted them with a septum through which water samples were taken with a syringe before and after each experiment.

Fig. 1. Experimental apparatus: (a) photograph of the tank; (b) schematic picture. Ice thickness was measured visually by removing part of the StyrofoamTM at 3 hourly intervals.
2.2. Experiments and processing
Before starting this experiment, the tank was cooled uniformly to a room temperature of −1°C, with occasional stirring. After the water temperature had settled to about −1°C, we set the room temperature at −5°C, −7.5°C, −10°C, −12.5°C, −15°C or −20°C and began to grow sea ice at each temperature. When the ice thickness reached ∼5 cm, we used a saw to cut out a rectangular ice block with a basal area of 0.2 m × 0.2 m. Immediately after collecting the ice block, we transferred it to another cold room set to −15°C. It remained there until ready for ice structure analysis.
In the cold room, the ice block was divided into four sections with a basal area of 0.1 m × 0.1 m. One section was used for thick-/thin-section analysis of textural structure, two sections were used to measure ice density, salinity and δ18O and the fourth section was archived. Thin (<1 mm) and thick (5 mm) sections were analyzed to observe, respectively, the crystallographic alignments with crossed linear polarizers and the structure of inclusions with scattered light. One example grown at a room temperature of −15°C is shown in Figure 2. As shown in Figure 2b, ice texture is composed mainly of four types: (1) a vertical c-axis layer (0–0.5 cm depth), (2) a transition layer (0.5–2.0 cm), (3) an inner columnar layer (2.0–3.5 cm) and (4) a bottom columnar layer (3.5–5.0 cm). The ice section was sliced into these four segments to measure density, salinity and δ18O. A bottom columnar layer was categorized separately because it exhibited different properties (e.g. significantly higher salinity and brine volume fraction than the inner columnar layer, as shown in Table 1). The ice density was determined from the weight and dimensions of each segment, with an estimated accuracy of ∼1%. The salinity and δ18O were measured for the melted ice segments with a salinometer (TOWA Electronic Industry, model SAT-210) and an isotope ratio mass spectrometer (Thermo Finnigan DELTA plus), respectively. The measurement method of δ18O is dual inlet based on Reference Epstein and MayedaEpstein and Mayeda (1953). The instrumental accuracy of salinity is <0.05. The analytical precision of δ18O is estimated to be 0.02‰ from the root mean square of the differences in values of two measurements on the same sample for all samples. The brine volume fraction was calculated from ice temperature, density and salinity from the formula of Reference Cox and WeeksCox and Weeks (1983) at each layer.
Table 1. One example of the vertical profiles obtained for a room temperature of −15°C. See Figure 2 for the depths of layers 1–4


Fig. 2. One example of the textural structure of sea ice grown at a room temperature of −15°C. (a) Thick section (5 mm thick); (b) thin section (1 mm thick). 1. Vertical c-axis layer (0.0–0.5 cm depth); 2. transition layer (0.5–2.0 cm); 3. inner columnar layer (2.0–3.5 cm); 4. bottom columnar layer (3.5–5.0 cm).
An example set of results, obtained at a room temperature of −15°C, is shown in Table 1. This table shows that each layer has characteristic properties: the first layer is characterized by low density, low salinity and high εeff, si, the second layer by low εeff, si, the third layer by high density and the fourth layer by low density and significantly high salinity. In this study, particular attention is paid to the inner columnar layer (layer 3) as a commonly observed sea-ice type. Another noticeable result in Table 1 is the increase in salinity (2.14) and the decrease in δ18O (−0.15‰) of sea water during the experiment. Regarding the increase in salinity, the resultant decrease of the freezing point is estimated to be only 0.1°C, so its effect on the result is assumed to be negligible. On the other hand, the decrease in δ18O corresponds to about one-tenth ofεeff, si. Thus the effect is non-trivial and careful analysis is required to estimate εeff, si.
2.3. Estimation of effective fractionation coefficient (εeff, si )
In general, when we conduct a freezing experiment in a closed system, the isotope ratio of the remaining sea water (R SW) changes due to the formation of sea ice. To derive a relation for the effective fractionation coefficient in terms of the original sea-water δ18O and the δ18O of ice, the evolution of RSW should be calculated from the following Rayleigh equation (Reference HoefsHoefs, 2009):
whereRSW0 is the isotope ratio of the initial sea water and R SW is the instantaneous isotope ratio of the remaining sea water, f is the fraction of the remaining sea water (VSW) to the initial volume (VSW0) and α is the fractionation factor given by R ice /R sw.
Since ln ![]() , Eqn (1) can be expressed as
, Eqn (1) can be expressed as

where εeff, si is equal to δ18Oice–δ18OSW. Then the following equation can be derived:

The value of εeff, si at each layer can be obtained by substituting into Eqn (3) V SW/V SW0 = 59.8 cm/60 cm for the first layer, 58.8 cm/60 cm for the second layer, 57.3 cm/60cm for the third layer and 55.8 cm/60 cm for the fourth layer. The result applied to a room temperature of −15°C is presented in Table 1. By taking the thickness-weighted average, the bulk mean εeff, si of the total layer is estimated as 1.59‰. If this value is substituted into Eqn (2), the change in δ18O of sea water during the experiment is expected to be −0.14‰, which coincides approximately with the observed value of −0.15‰, obtained by taking the average of the δ18O of sea water at depths of 5, 15, 25, 35, 45 and 55 cm, within the measurement accuracy (Table 1). Therefore our method of estimating εeff, si seems reasonable.
2.4. Estimation of growth rates
The growth rates in each layer were calculated from the slope of the thickness-versus-time curve, within the layer, by a least-squares method. For example, in the case of an inner columnar layer we estimated the slopes and the confidence interval at the 95% level by using the thickness data between ∼2.0 and 3.5 cm (Fig. 3). The results for various room temperatures for each layer are listed in Table 2, which shows that the growth rates range from (2.25 ± 0.50) × 10−7 m s−1 for −5°C to (9.28 ± 2.08) × 10−7 m s−1 for −20°C for layer 3. For other layers, the growth rates ranged from 1.81 × 10−7 m s−1 (−5°C) to 6.75 × 10−7 m s−1 (−20°C) (layer 1), from 3.17 × 10−7 to 9.16 × 10−7 m s−1 (layer 2) and from 1.81 × 10−7 to 9.33 × 10−7 m s−1 (layer 4) (Table 2). Whereas the growth rate was relatively slow for layer 1, it was comparable in the other layers, indicating that the sea ice grew at a near-constant rate except at the early stage. The effect of ocean heat flux transferred from sea water to sea ice was not taken into account here since the sea water underlying sea ice was kept at ∼−2.0°C, somewhat below the freezing temperature (−1.7°C), in each case while sea ice was grown. Consequently a number of thin platelet ice crystals with a height of a few centimeters extended from the bottom of the sea ice into water that appears to be supercooled. Therefore, the ocean heat transfer from sea water to ice is considered not to be positive.
Table 2. Growth rates of each ice layer obtained for individual room temperatures


Fig. 3. Evolution of ice thickness as a function of time for each experiment. The growth rate at the inner columnar layer was obtained from the slope of the 2.0–3.5 cm thickness data.
3. Observations
3.1. McMurdo Sound, Antarctica
We have analyzed samples of columnar landfast sea ice from McMurdo Sound, Antarctica. Lying at the southwestern end of the Ross Sea, McMurdo Sound is bounded to the south by the McMurdo Ice Shelf, to the west by the Victoria Land coast and to the east by Ross Island (Fig. 4a).

Fig. 4. (a) Sampling locations in McMurdo Sound, Antarctica. The open triangle indicates the 1999 sampling site and the solid triangle indicates the 2009 sampling site. (b) Sampling locations in the Sea of Okhotsk with approximate ice edges. The dashed, thin solid and thick solid lines denote the ice edges for 2003, 2004 and 2005, respectively. Solid circles show the sampling sites during 2003–05, while the open circle and open square show the site of the sample in Figure 10 and the ERA-Interim gridpoint, respectively, for validation.
The landfast sea ice in McMurdo Sound has been the subject of intensive scientific investigation since the early 20th century (Reference Wright and PriestleyWright and Priestley, 1922). Most papers reporting on McMurdo Sound sea-ice structure have noted the presence of incorporated platelet ice, at least in the latter part of the growth season (e.g. Reference PaigePaige, 1966; Reference Crocker and WadhamsCrocker and Wadhams, 1989; Reference Jeffries, Weeks, Shaw and MorrisJeffries and others, 1993; Reference Gow, Ackley, Govoni, Weeks and JeffriesGow and others, 1998; Reference Purdie, langhorne, Leonard and HaskellPurdie and others, 2006; Reference Gough, Mahoney, Langhorne, Williams, Robinson and HaskellGough and others, 2012a). This paper focuses on columnar ice only; therefore, data from the latter part of the growth season when incorporated platelet ice was observed are not included in our analysis.
3.1.1. 1999 data
Two 1999 McMurdo Sound measurements of sea-ice growth rates for columnar ice were included in the analysis, along with the corresponding values of εeff, si, calculated from the δ18O sea-ice measurements in conjunction with the end-ofseason δ18O sea-water measurement. Core sampling was conducted on 24 August and sea-water sampling was conducted on 23 August. Full details of the equipment used, location and methodology are given by Reference Smith, Langhorne, Frew, Vennell and HaskellSmith and others (2012). The other growth-rate and εeff, si data reported in that paper are not included here due to the presence of incorporated platelet ice.
3.1.2. 2009 data
Seven 2009 McMurdo Sound measurements of columnar sea-ice growth rates were included in the analysis, along with the corresponding values of εeff, si, calculated from the mean of δ18O sea-ice measurements at each depth in cores taken throughout the growth season, in conjunction with the δ18O sea-water measurement taken close to the end of the observation period. Sea-ice cores were collected on 22 June, 10 August, 21 September and 27 September. Full details of the equipment used, location and methodology are given by Reference Gough, Mahoney, Langhorne, Williams, Robinson and HaskellGough and others (2012a). Samples in which incorporated platelet ice was observed are not included in the present analysis.
The sea-water sample used in the analysis was from 10 m depth below the water surface at the Erebus Bay site on 23 July 2009 (δ18O = −0.61‰). This sample was selected as it was collected when only columnar ice was present (i.e. it is not affected by the presence of platelet ice) (Fig. 4a; Reference Gough, Mahoney, Langhorne, Williams, Robinson and HaskellGough and others, 2012a). When sampling sea water, much care was taken to ensure that freezing did not occur. Seawater samples were collected sporadically from June to September in 2009 (N = 12) while the ice-core samples were collected. The sample statistics show the mean to be −0.61 ± 0.06‰. A Niskin bottle (NIO configuration) was used to sample water. Some water was allowed to drain from the bottle when it was brought to the surface before the sample water was sieved and used to double-rinse the 100 mL glass vials before two vials were filled (leaving a small air gap) and then sealed with lids that had rubber inserts. The vial lids were then taped tightly shut. The vials were stored in darkness at ∼15°C at Scott Base over the 2009 winter and transported by airplane to New Zealand for measurement of δ18O.
For sea ice, stable-isotope samples were retained from salinity samples after the salinity of the melted samples had been measured (Reference Gough, Mahoney, Langhorne, Williams and HaskellGough and others, 2012b). Sections of ice 10 cm in vertical thickness were cut from freshly extracted ice cores and quickly placed in plastic pots with lids. The pots were transported cold to Scott Base and melted over a 2 day period. Once melted, samples were opened, stirred and measured with a salinometer. The sample was then used to prepare two glass vials for later isotopic analysis using a similar procedure to that described above for the sea-water sample. Only one sample was retained from each segment of each core sampled, but on most occasions two cores taken at the same location and time were used to prepare independent stable-isotope samples.
Oxygen isotope analysis was carried out at the Department of Chemistry, University of Otago. Oxygen isotope ratios in the samples were analysed by continuous flow mass spectrometry. Aliquots (0.5 mL) of sample were equilibrated with CO2 (0.3% in He) for at least 18 hours at 25°C. After equilibration, the CO2 was analysed utilizing a GasBench (Thermo Finnigan, Bremen, Germany) interfaced to a Delta Plus Advantage mass spectrometer (Thermo Finnigan, Bremen, Germany). Three water standards of known value were run with each set of samples, and the isotope ratios of the samples were normalized to the Vienna Standard Mean Ocean Water (VSMOW) scale. Mean precision (the repeatability of a measurement on a single sample) for all ice and ocean samples was ±0.05‰.
3.2. Sea of Okhotsk
The southern Sea of Okhotsk is at one of the lowest latitudes in the world where a sea-ice cover exists. The sea-ice extent is at its largest at the end of February and the level ice thickness is mostly <1 m, with the mean being 0.3–0.5 m (Reference Toyota, Kawamura, Ohshima, Shimoda and WakatsuchiToyota and others, 2004), although ridged ice more than a few meters thick occasionally appears (Reference Fukamachi, Mizuta, Ohshima, Toyota, Kimura and WakatsuchiFukamachi and others, 2006). In this region, sea-ice observations have been carried out in collaboration with the Japan Coast Guard on board the icebreaker P/V Soya in early February every winter since 1996, corresponding to the ice growth season, to survey the ice and oceanographic conditions and to tackle ad hoc topics related to sea ice.
During 1996–99, focus was placed on the estimation of the surface heat budget to reveal the transformation process of the air mass that originates over Siberia (Reference Toyota and WakatsuchiToyota and Wakatsuchi, 2001). For this purpose, we conducted measurements of meteorological data (air temperature, pressure, relative humidity, wind, incident and reflected solar radiation, cloud) and of ice conditions (ice concentration, types, thickness) along the ship’s track. Ice concentration and types were observed visually according to the ASPeCt (Antarctic Sea Ice Processes and Climate) protocol, which was designed for ship-based observations in Antarctic seas (Reference Worby and AllisonWorby and Allison, 1999), and ice thickness was monitored using a video monitoring system (Reference Toyota, Kawamura, Ohshima, Shimoda and WakatsuchiToyota and others, 2004). While the observation period was limited to ∼1 week, the ship’s tracks covered a wide area of the southern Sea of Okhotsk. Therefore, we examined the representative diurnal variation of the surface heat budget in this area from hourly averaged meteorological data. In our calculations, we used a thermodynamic ice model similar to that of Reference MaykutMaykut (1978, Reference Maykut1982) based on the obtained ice thickness distribution. As a result, it was found that sea ice grows only at night-time due to abundant daytime solar radiation at low latitudes at that time of year. The averaged night-time growth rates were estimated to be 2.78, 1.61, 3.58 and 2.19 × 10−7 m s−1 for the years 1996–99, respectively (Reference Toyota and WakatsuchiToyota and Wakatsuchi, 2001). Taking the average of this result, we use (2.54 ± 0.83) × 10−7 m s−1 as a representative growth rate in this region.
During 2003–05, our major topic of investigation was the properties of sea ice and overlying snow in this region (Reference Toyota, Takatsuji, Tateyama, Naoki and OhshimaToyota and others, 2007). For this purpose, we collected 27 ice samples, ranging from 6 to 225 cm in thickness, with a core auger and then analyzed the crystallographic alignments and the vertical profiles of density, δ18O and salinity at 3 cm depth intervals. The sampling locations are plotted in Figure 4b. δ18O of columnar ice was shown to be 0.9 ± 0.3‰ (mean ± 1 std dev.; N = 301) (Reference Toyota, Takatsuji, Tateyama, Naoki and OhshimaToyota and others, 2007). In addition, the δ18O of the surface sea water was shown to be −1.0 ± 0.2‰ (mean ± 1 std dev.) from the samples collected over a wide area during the same cruises. Since the δ18O distributions of both sea ice and sea water follow an almost normal distribution, the representative effective fractionation coefficient (εeff, si) of columnar ice is estimated statistically to be 1.88 ± 0.10‰ from the difference of the distributions. Although the observation period is different from that for the growth rate estimation, there was no significant difference in the meteorological and ice conditions between these two periods: for example the mean air temperatures and level ice thicknesses were −5.2, −4.1 and −10.1°C and 0.42, 0.60 and 0.42 m for 2003–05 and −5.0, −5.4, −8.1 and −5.0°C and 0.18, 0.55, 0.30 and 0.29 m for 1996–99, respectively. Therefore we regard (2.54 ± 0.83) × 10−7 m s−1 and 1.88 ± 0.10‰ as the representative values of ice growth rate and εeff, si in winter in this region. Since the estimation of growth rate is not a direct measurement, these data are to be used mainly to provide some support for the derived parameterizations.
4. Summary of the Stagnant Boundary-Layer Model
Prior to showing the results, we briefly describe the stagnant boundary-layer (SBL) model. The SBL model was introduced by Reference Burton, Prim and SlichterBurton and others (1953) to explain theoretically the incorporation of impurity into single crystals frozen from melt. The model divides the sea water into a fixed-depth boundary layer adjacent to the bottom of the sea ice and an underlying well-mixed layer (Fig. 5). Within the boundary layer, δ18O is taken to decrease toward the ice as it is affected by fractionation due to bottom freezing, hence a purely diffusive process is dominant in this layer. Within the well-mixed layer, δ18O is kept constant by convection and advection.εeff, si is defined as the difference between the δ18O of the sea ice near the ice–water interface and the δ18O of the well-mixed layer. According to this model, the equation of the solute concentration (CL ) within the boundary layer is described as (Reference Burton, Prim and SlichterBurton and others, 1953)

Fig. 5. Schematic of the stagnant boundary-layer (SBL) model. z = 0 is set at the bottom of the sea ice and zbl is assumed to be constant. The effective fractionation coefficient of ice (εeff,i) is calculated from εeff, i = (αi ∼ 1) 1000 (‰).
where D is a molecular diffusivity, z is the vertical coordinate and v i is growth rate. In our case, CL corresponds to the isotope ratio normalized by VSMOW, i.e.

and D, the diffusivity of H2 18O at −2°C, is set to 1.20 × 10−9 m2 s−1 (Reference LevineLevine, 1983). The boundary condition is given by

at the interface (z = 0) CL = C LB at z = z bl, where C 0 is the value of CL at z = 0, C LB is the constant value of CL in the mixed layer and α eq *, the equilibrium fractionation factor, is equal to 1 + εeq * /1000. By solving these equations under the steady-state conditions, the following equation can finally be derived:

where εeff, i is the effective fractionation coefficient between pure ice and sea water and is described asi
![]() where CS
(0) is
where CS
(0) is  .
.
Furthermore, by taking into account the entrapment of brine into sea ice, Reference Eicken and JeffriesEicken (1998) derived the following formula correlating εeff, si with v i for sea ice:
where K eff, S denotes salt segregation in a newly grown ice layer and is given as a function of v i according to Reference Cox and WeeksCox and Weeks (1975) based on experimental data as follows:

Reference Cox and WeeksCox and Weeks (1975) set this threshold because their experimental data started to deviate from the line for growth rates less than 2.0 × 10−7 m s−1 (fig. 32 in Reference Cox and WeeksCox and Weeks, 1975). They inferred that the change in slope is probably due to a change in the morphology of the ice–water interface. However, as shown in Figure 6, there is some discontinuity at the threshold. To smooth this discontinuity, Reference Cox and WeeksCox and Weeks (1988) introduced a second formula with a new threshold of 3.6 × 10−7 m s−1. In this paper, we adopt the formula and threshold of Reference Cox and WeeksCox and Weeks (1975) because we place higher priority on the underlying physical processes than on obtaining a smooth curve fit at the threshold and these two predicted curves almost coincide except around the threshold (Fig. 6).

Fig. 6. Comparison of salt segregation (keff,S) between Reference Cox and WeeksCox and Weeks (1975) and Reference Cox and WeeksCox and Weeks (1988) as a function of growth rates. Note that although the thresholds are different between these two formulae (2.0 × 10−7 m s−1 for Reference Cox and WeeksCox and Weeks (1975) and 3.6 × 10−7 m s−1 for Reference Cox and WeeksCox and Weeks (1988)), the predicted curves almost coincide except around the threshold.
The application of the formula of Reference Cox and WeeksCox and Weeks (1975) to our experimental data was found to produce reasonable predictions of k eff, S based on an analysis of sea-ice salinity. For example, when it is applied for the cases of room temperatures of −10°C and −15°C (with corresponding growth rates of 4.24 and 5.83 × 10−7 m s−1 in the bottom columnar layer, respectively),k eff, S is predicted to be 0.32 and 0.35 and the corresponding layer salinity to be 11.3 and 11.9 psu, respectively. Our analysis shows that the salinity of this layer was 11.0 and 11.6 psu, respectively. Considering that some desalinization occurs when removing the ice block, the data are close to the values predicted by this formula.
Consequently, the key parameters in Eqns (7) and (8) are α eq * (or εeq *) and zbl. Reference Eicken and JeffriesEicken (1998) used εeq * = 2.91‰ from the experimental result for pure ice (Reference Lehmann and SiegenthalerLehmann and Siegenthaler, 1991) and deduced zbl = 1.3 mm. Our interest is to examine the applicability of the variables used in the model of Reference Eicken and JeffriesEicken (1998). It is well known that the interface between sea ice and sea water is more complicated than is shown in Figure 5, due to groove structure, brine rejection and advective fluid exchange between sea water and sea ice (e.g. Reference Niedrauer and MartinNiedrauer and Martin, 1979). Although mushy-layer theory is a physically realistic model capable of simulating the behavior of brine in sea ice (e.g. Reference WorsterWorster, 1997; Reference Feltham, Untersteiner, Wettlaufer and WorsterFeltham and others, 2006), its ability to predict sea-ice parameters has not been tested as extensively against measurements as the SBL parameterizations. Mushy-layer theory also requires several parameters, such as permeability or brine concentration, which are difficult to measure. We have therefore adopted the SBL model here for pragmatic reasons, since it is a useful way to parameterize the physical process that has been successfully used to explain the segregation processes associated with crystal growth.
5. Results
The columnar ice data obtained from field observations and the laboratory experiment are plotted in Figure 7a, which shows that although the data from Antarctica and the experiment cover separate ranges of growth rates, they can be connected at a growth rate of about 2.0 × 10−7 m s−1 (the threshold of Reference Cox and WeeksCox and Weeks, 1975) and that the data from the Sea of Okhotsk lie approximately on the line of the experimental data. We therefore combined the Antarctic field observations dataset and the laboratory experiment dataset in order to investigate processes over the full range of growth rates.

Fig. 7. Effective fractionation coefficients between sea ice and sea water as a function of ice growth rates, focusing on columnar ice, obtained by combining the data from field observations and laboratory experiments. (a) Data from field observations and laboratory experiments plotted with the curves of Reference Eicken and JeffriesEicken (1998) and modified Reference Eicken and JeffriesEicken (1998) based on the SBL model. The curves of modified Reference Eicken and JeffriesEicken (1998) (1) and (2) were drawn based on Antarctic field data, where z
bl = 0.90 mm and ![]() , and on laboratory experiments, where z
bl = 0.10 mm and
, and on laboratory experiments, where z
bl = 0.10 mm and ![]() , respectively, whereas z
bl = 1.3 mm and
, respectively, whereas z
bl = 1.3 mm and ![]() in Reference Eicken and JeffriesEicken (1998). (b) Fitting curve of Eqn (9) obtained for practical use from modified Reference Eicken and JeffriesEicken (1998) ((1) for v
i < 2.0 × 10−7 m s−1 and (2) for v
i > 2.0 × 10−7 m s−1) plotted with data from the field observations and laboratory experiments.
in Reference Eicken and JeffriesEicken (1998). (b) Fitting curve of Eqn (9) obtained for practical use from modified Reference Eicken and JeffriesEicken (1998) ((1) for v
i < 2.0 × 10−7 m s−1 and (2) for v
i > 2.0 × 10−7 m s−1) plotted with data from the field observations and laboratory experiments.
We then applied the model of Reference Eicken and JeffriesEicken (1998), which is based on the SBL model, to our results to examine the optimal values of the physical parameters used in the model. The curve of Reference Eicken and JeffriesEicken (1998) is superimposed on Figure 7a. It is found that overall the model of Reference Eicken and JeffriesEicken (1998) underestimates εeff, si, as pointed out by Reference Smith, Langhorne, Frew, Vennell and HaskellSmith and others (2012). The laboratory experiment and Sea of Okhotsk observational data presented here show significant deviation from the Reference Eicken and JeffriesEicken (1998) model at growth rates larger than about 2.0 × 10−7 m s−1.
To improve this model, we first attempted to use the form of the Reference Eicken and JeffriesEicken (1998) equation and performed regression analysis using least-squares fitting to select values of the parameters zbl and ![]() that fit all the growth rate data. However, that attempt proved unsuccessful because the slope of the curve at ∼2.0 × 10−7 m s−1 increased significantly for decreasing growth rates. Hence we separately examined the optimal parameters for field observations in Antarctica (v
i < 1.7 × 10−7 m s−1) and the laboratory experiment (v
i > 2.2 × 10−7 m s−1) to minimize the root-meansquare error (RMSE). As a result, we obtained
that fit all the growth rate data. However, that attempt proved unsuccessful because the slope of the curve at ∼2.0 × 10−7 m s−1 increased significantly for decreasing growth rates. Hence we separately examined the optimal parameters for field observations in Antarctica (v
i < 1.7 × 10−7 m s−1) and the laboratory experiment (v
i > 2.2 × 10−7 m s−1) to minimize the root-meansquare error (RMSE). As a result, we obtained ![]() and z
bl = 0.9 ± 1.9 mm at the 95% confidence level for v
i< 2.0 × 10−7 m s−1, and
and z
bl = 0.9 ± 1.9 mm at the 95% confidence level for v
i< 2.0 × 10−7 m s−1, and ![]() and z
bl = 0.1 ± 0.1 mm at the 95% confidence level for v
i > 2.0 × 10−7 m s−1. The curves for both cases are drawn in Figure 7a. Slight gaps seen at v
i = 2.0 × 10−7 m s−1 come from the discontinuity in k
eff, S of Reference Cox and WeeksCox and Weeks (1975), as mentioned before. Thus significantly different sets of parameters were obtained for the two ranges of growth rates. It is especially noticed that while the values of zbl and
and z
bl = 0.1 ± 0.1 mm at the 95% confidence level for v
i > 2.0 × 10−7 m s−1. The curves for both cases are drawn in Figure 7a. Slight gaps seen at v
i = 2.0 × 10−7 m s−1 come from the discontinuity in k
eff, S of Reference Cox and WeeksCox and Weeks (1975), as mentioned before. Thus significantly different sets of parameters were obtained for the two ranges of growth rates. It is especially noticed that while the values of zbl and ![]() are close to those of Reference Eicken and JeffriesEicken (1998) (1.3 mm and 2.91‰) and to Reference Smith, Langhorne, Frew, Vennell and HaskellSmith and others (2012) (2.2 mm and 3.4‰), which were estimated for lower growth rates (<1.3 × 10−7 m s−1) but including platelet ice, for higher growth rates z
bl is an order of magnitude smaller and
are close to those of Reference Eicken and JeffriesEicken (1998) (1.3 mm and 2.91‰) and to Reference Smith, Langhorne, Frew, Vennell and HaskellSmith and others (2012) (2.2 mm and 3.4‰), which were estimated for lower growth rates (<1.3 × 10−7 m s−1) but including platelet ice, for higher growth rates z
bl is an order of magnitude smaller and ![]() is also significantly smaller. Relatively significant errors of z
bl for both regimes may suggest the limitations of the SBL model.
is also significantly smaller. Relatively significant errors of z
bl for both regimes may suggest the limitations of the SBL model.
We next considered what may have led to the two regimes. One possibility might be that various factors could affect the fractionation process in field observations, whereas the laboratory experiment was much simpler. However, the fact that the datum from the Sea of Okhotsk lies approximately on the curve derived primarily from the experimental data in Figure 7a suggests that the growth rate may be a controlling factor in determining εsi, at least for v i > 2.0 × 10−7 m s−1. The detail is discussed further in Section 6.
Finally, for practical use we sought to derive an empirical formula that predicts εeff, si from v i in m s−1 with good accuracy over the range of velocities of both the Antarctic and laboratory experiment datasets. Although there were different regimes in the modified Reference Eicken and JeffriesEicken (1998) model at a threshold of 2.0 × 10−7 m s−1, for simplicity we obtained a single regression formula covering the whole range of v i by fitting the output of the modified Reference Eicken and JeffriesEicken (1998) model at intervals of 0.1 × 10−7 m s−1 with a least-squares method as follows.
For 0.8 × 10−7 m s−1 < v i < 9.3 × 10−7 m s−1
where a 1 = 1.2280‰, b 1 = 0.7311‰, c 1 = 8.0100 × 10−8 m s−1, d 1 = 0.8441‰ and e 1 = 0.7800 × 10−6 m s−1. Equation (9) is drawn in Figure 7b. In fitting the curve, we used modified Reference Eicken and JeffriesEicken (1998) model output instead of the measured values to ensure that all parts of the curve were equally biased. Using a similar procedure to that above, an inverse function for v i as a function of εeff, si was obtained from Eqn (9):
For 1.47‰ < εeff, si < 2.38‰
where a 2 = 2.7570 × 10−8 m s−1, b 2 = 1.1000 × 10−4 m s−1 , c 2 = 0.3226‰, d 2 = −1.5430 × 10−6 m s−1 and e 2 = 0.6800‰. Equations (9) and (10) are discussed further in a case study in the Sea of Okhotsk in Section 6.3.
6. Discussion
6.1. Effects of other factors
So far we have examined the dependence of ε on v i using Eicken’s model, which was derived from the SBL model. In general, it is known that fractionation is also affected by other factors such as grain size and grain shape due to differences in crystal structure (Reference HoefsHoefs, 2009). Here we examine the effect of these factors on εeff, si. This may provide some insight into how two regimes are apparent when εeff, si is plotted with respect to v i. To approach this issue, first we show the results of non-columnar ice types obtained from our laboratory experiment. As shown in Table 1, layer 1 (2) has significantly higher (lower) isotope fractionation than the inner columnar layer, layer 3. These layers, corresponding to vertical c-axis and transition layers, have significantly larger and smaller grain sizes, respectively, than the columnar ice layer. Therefore, it is likely that grain size and shape also affected εeff, si. However, since v i varied depending on each layer, we need to separate out the effect of v i. To do so, in Figure 8 we plot the data obtained from all the layers. Figure 8 clearly shows that even at the same growth rate, layers 1 and 2 tend to have higher and lower values of εeff, si, respectively, while layers 3 and 4, which are composed of similar columnar ice, have almost comparable εeff, si. This indicates that grain size and type (i.e. granular or columnar ice) affect εeff, si significantly and should be taken into account in the determination of εeff, si.

Fig. 8. Fractionation coefficients (εeff, si) at each layer as a function of growth rates. 0.5, 2.0, 3.5 and 5.0 cm denote the layers 0.0–0.5, 0.5–2.0, 2.0–3.5 and 3.5–5.0 cm, respectively. Growth rates were estimated for individual layers
Next we consider if the substructure of sea ice can affect εeff, si for the same columnar ice. The characteristic size in the substructure of columnar ice is represented by brine layer spacing (a
0). The results obtained from field observations in the Arctic by Reference Nakawo and SinhaNakawo and Sinha (1984) and Reference Sinha and ZhanSinha and Zhan (1996) showed that a
0 tends to be inversely proportional to v
i within the range 0.8 × 10−7 < v
i < 2.0 × 10−7 m s−1 in accordance with the theoretical prediction by Reference Bolling and TillerBolling and Tiller (1960). According to the observational results of Reference Nakawo and SinhaNakawo and Sinha (1984) and Reference Sinha and ZhanSinha and Zhan (1996), a
0 doubled from 0.5 to 1 mm with a decrease in v
i from 2.0 × 10−7 to 0.8 × 10−7 m s−1. Reference Bolling and TillerBolling and Tiller (1960) and Reference Lofgren and WeeksLofgren and Weeks (1969) suggested that the relationship becomes inversely proportional between a
0 and ![]() for large growth rates, which means less dependence of a
0 on v
i for large v
i. Therefore it may be possible that such a significant increase in grain size contributed to producing a different regime for small growth rates (v
i < 2.0 × 10−7 m s−1 ). Besides, observational results show that a
0 also depends somewhat on ocean current direction relative to the c-axis (Reference Nakawo and SinhaNakawo and Sinha, 1984) and ocean current speed (Reference Eicken, Thomas and DieckmannEicken, 2003), indicating that ocean current can also affect εeff, si. Consequently, various factors tend to affect the values of εeff, si especially for small v
i. This may also explain the large variability of εeff, si for the observation in the Antarctic observations in Figure 7a.
for large growth rates, which means less dependence of a
0 on v
i for large v
i. Therefore it may be possible that such a significant increase in grain size contributed to producing a different regime for small growth rates (v
i < 2.0 × 10−7 m s−1 ). Besides, observational results show that a
0 also depends somewhat on ocean current direction relative to the c-axis (Reference Nakawo and SinhaNakawo and Sinha, 1984) and ocean current speed (Reference Eicken, Thomas and DieckmannEicken, 2003), indicating that ocean current can also affect εeff, si. Consequently, various factors tend to affect the values of εeff, si especially for small v
i. This may also explain the large variability of εeff, si for the observation in the Antarctic observations in Figure 7a.
Another possible effect is the enhancement of the interface area (A i) between sea ice and sea water and the groove structure of the bottom surface. With an increase in the interface area, εeff, si is expected to increase compared with its value for a planar bottom. Normally the bottom surface of columnar ice is not flat but is composed of numbers of knife-edged cells with spacings (a 0) of ∼0.5–2.0 mm and depth (h) of a few to tens of millimeters (Reference KovacsKovacs, 1996; Reference Eicken and JeffriesEicken, 1998). A schematic is shown in Figure 9b. If we assume the two-dimensional (vertical and horizontal) structures and approximate them by triangles, the enhancement of the interface area is calculated as

where A 0 is the area of the flat bottom (Fig. 9a). The ratio A i/A 0 is shown as a function of h and a 0 in Figure 9c. As mentioned above, a 0 tends to decrease with an increase in v i. Besides, although the geometry of the groove structure of the sea-ice bottom surface has not yet been clarified, in metals the tip of the groove structure is known to become sharpened with the increase in v i (Reference WeeksWeeks, 2010), indicating the increase in h/a 0with v i in Eqn (11). Thus, if this is applicable to sea ice, the ratioAi/A0 is expected to become enhanced with an increase in v i from 0.8 × 10−7 to 2.0 × 10−7 m s−1. Noticeable in Figure 9c is that especially around a 0 ∼0.5 mm, corresponding to v i ∼ 2.0 × 10−7 m s−1, the sensitivity to both a 0 and h becomes enhanced significantly. This may explain why εeff, si for the experimental data takes significantly larger values than those predicted by the curve obtained from the Antarctic observations. The fact that the area enhancement is highly dependent on v i may also contribute to the strong dependency of εeff, si on v i, especially for v i > 2.0 × 10−7 m s−1 . Eicken’s model included the effect of change in brine volume entrapped in sea ice as a function of v i. Our results suggest that v i may play an important role in determining εeff, si, not only through a change in brine volume, but also via the change in geometric features such as grain size or brine layer spacing, not limited to the change in brine volume.

Fig. 9. Schematic of the effect of groove structure on ε eff,si. (a) Ideal sea ice with flat bottom; (b) real sea ice with groove structure at the bottom; (c) ratio of the bottom surface b to a as a function of groove depth (h) and spacing (a 0). 0.25, 0.50, 1.00, 1.50 and 2.00 denote the spacing of the groove (mm).
6.2. Response depth to the change of a growth rate
When we apply the εeff,i–v
i relationship of Eqn (7), obtained under steady-state conditions, to real sea ice that grows at various growth rates, we need to consider the response time, or response depth in sea ice, required to adjust to the change in v
i. Since the change in v
i leads to a gradual adjustment of C
0 and subsequently εeff,i, it is expected to take some time before εeff,i reaches a stable value determined by Eqn (7). If the ice growth amount during the adjustment period (referred to hereafter as response depth) is large enough, Eqn (7) would not necessarily be useful for estimating growth rates from the δ18O profile of sea ice. Thus the response depth is critical to the analysis of δ18O and needs to be examined. Here, as an example of a significant change in v
i, we estimate the response depth when sea ice starts to grow. This case is applicable to the Sea of Okhotsk, where ice growth is limited to night-time, as described in Section 3.2. For this purpose, we solved Eqn (4) numerically with the boundary conditions of Eqn (6) using an explicit scheme (forward in time, central in space). A time-step Δt and grid spacing Δz were set to 1.0 s and 0.05 mm, respectively, so that the computational condition Δt ≤ (Δz)2
/(2D) ∼ 1.04 s is satisfied. Physical parameters z
bl and ![]() were taken to be 2 mm and 2.91‰, respectively, as a possible large value for z
bl and after Reference Eicken and JeffriesEicken (1998) for
were taken to be 2 mm and 2.91‰, respectively, as a possible large value for z
bl and after Reference Eicken and JeffriesEicken (1998) for ![]() . Here the δ18O of bulk sea water is assumed to be −0.8‰, based on the tank experiment. According to Eqn (4), the isotope ratio CL
at the nth time-step and the ith layer within the boundary layer, CL
(n,i), is calculated by:
. Here the δ18O of bulk sea water is assumed to be −0.8‰, based on the tank experiment. According to Eqn (4), the isotope ratio CL
at the nth time-step and the ith layer within the boundary layer, CL
(n,i), is calculated by:

with the initial condition ![]() and the boundary condition
and the boundary condition

The profile of δ18O in sea water was obtained by converting CL
to δ18O with Eqn (5), while the profile of δ18O in sea ice was obtained by converting ![]() to δ18O and multiplying v
i by time. In Eicken’s model, including the effect of the entrapped brine, εeff, si is obtained by multiplying εeff,i by (1 – keff,S), as shown in Eqn (8). However, when a constant growth rate is considered, neglecting this effect will not alter the result since keff,S is kept constant. Numerical simulations were conducted for v
i = 1.4 × 10−7 and 8.3 × 10−7 m s−1,representative of low and high growth rates in real sea ice. The result obtained by integrating Eqn (12) for 5 hours from the beginning of freezing is shown in Figure 10. Note that in this figure ice grows from the left end and the two vertical thick solid lines denote the individual ice–water boundaries. It is confirmed from Figure 10 that εeff, si depends significantly on v
i as Eqn (7) assumes. Further it is noticeable that the response depth also depends on v
i and is estimated to be about 0.5 and 2.0 mm for 1.4 × 10−7 and 8.3 × 10−7 m s−1,respectively. On the other hand, simple scale analysis from Eqn (4) provides the adjustment time (T
R) with ∼z
bl
2/D. Thus, the response depth (R
D) is approximately predicted:
to δ18O and multiplying v
i by time. In Eicken’s model, including the effect of the entrapped brine, εeff, si is obtained by multiplying εeff,i by (1 – keff,S), as shown in Eqn (8). However, when a constant growth rate is considered, neglecting this effect will not alter the result since keff,S is kept constant. Numerical simulations were conducted for v
i = 1.4 × 10−7 and 8.3 × 10−7 m s−1,representative of low and high growth rates in real sea ice. The result obtained by integrating Eqn (12) for 5 hours from the beginning of freezing is shown in Figure 10. Note that in this figure ice grows from the left end and the two vertical thick solid lines denote the individual ice–water boundaries. It is confirmed from Figure 10 that εeff, si depends significantly on v
i as Eqn (7) assumes. Further it is noticeable that the response depth also depends on v
i and is estimated to be about 0.5 and 2.0 mm for 1.4 × 10−7 and 8.3 × 10−7 m s−1,respectively. On the other hand, simple scale analysis from Eqn (4) provides the adjustment time (T
R) with ∼z
bl
2/D. Thus, the response depth (R
D) is approximately predicted:
By substituting the values, Eqn (13) gives R D ∼ 0.46 and 2.78 mm for 1.4 × 10−7 and 8.3 × 10−7 m s−1, which almost coincides with the result of the numerical simulation in Figure 9, indicating that Eqn (13) is reasonable for predicting R D. According to Eqn (13), R D is proportional to v i and z bl 2 . Since our simulation was done with the largest possible values of v i and z bl, the estimated R D (∼3 mm) is considered to be close to a maximum value. Therefore, it follows that the effect of the response depth on the profile of δ18O is essentially negligible.

Fig. 10. Profiles of δ18O of ice and water, obtained by numerical calculation for growth rates of 1.4 × 10−7ms− 1 (solid line) and 8.3 × 10−7ms− 1 (dashed line) 5 hours after the beginning of freezing. z
bl and ![]() are set to 2 mm and 2.91 %, respectively.
are set to 2 mm and 2.91 %, respectively.
6.3. Case study: application to the Sea of Okhotsk sea ice
As a case study, here we apply Eqns (9) and (10) obtained in Section 5 with a sea-ice sample collected in the seasonal ice zone to reveal the growth history. The ice sample was collected in the southern Sea of Okhotsk (see Fig. 4b for location) on 8 February 2010 as part of a sea-ice observation program in collaboration with the Japan Coast Guard. As shown in Figure 11a, this sample, having a thickness of 23 cm, was composed entirely of columnar ice except in the top 5 cm, where snow ice was present judging from its granular crystal structure and negative δ18O (Reference Toyota, Kawamura, Ohshima, Shimoda and WakatsuchiToyota and others, 2004). This indicates that the sea ice grew simply by a thermodynamic process for depths between 5 and 23 cm. The vertical profiles of δ18O and εeff, si are shown in Figure 11b, where εeff, si was estimated from the difference in δ18O between sea ice and sea water (−1.02 ± 0.21‰).
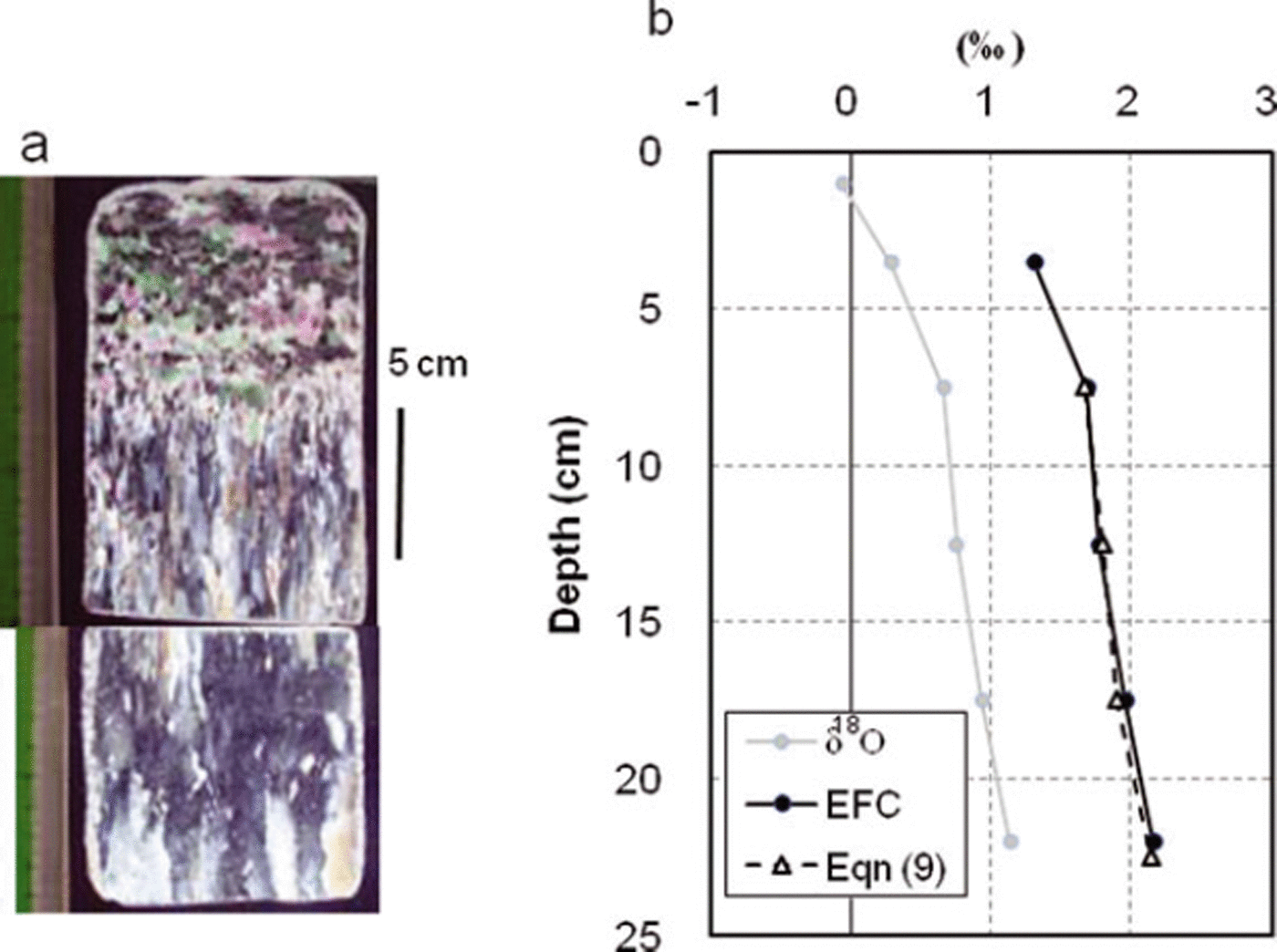
Fig. 11. Vertical profiles of sea-ice sample collected on 8 February 2010 in the southern Sea of Okhotsk (see Fig. 4b for location). (a) Crystal alignments by thin-section analysis. (b) δ18O (thin line), observed ε eff, si (solid circles with thick solid line) and predicted ε eff, si (triangles with thick dashed line). Observed ε eff, si at the top layer is omitted because it is snow ice. Predicted ε eff,si is obtained by calculating ε eff, si with Eqn (9) for night-time growth rate on each day and averaging the values for each 5 cm depth from the bottom.
Ice growth rates were estimated with a one-dimensional thermodynamic model in a similar way to that of Reference Toyota and WakatsuchiToyota and Wakatsuchi (2001). Meteorological data (air temperature, pressure, wind, cloud, relative humidity) were taken from the European Centre for Medium-Range Weather Forecasts Interim Re-analysis (ERA-Interim) dataset (1.5° × 1.5°) four times per day (03:00, 09:00, 15:00, 21:00 Japan Standard Time (JST)). Ice growth amount was calculated at a gridpoint (45° N, 144° E) near the observation site (Fig. 4b). Comparison between the ERA-Interim dataset at this gridpoint and observational data recorded on the ship in this area (44.4–45.5° N, 142.1–144.6° E) during the period 5–9 February 2010 showed that the ERA-Interim dataset reproduced the real meteorological conditions well, with an RMSE of 2.0 hPa for sea-level pressure, 1.5°C for air temperature and 3.8 m s−1 for wind speed. We assumed that ocean heat flux is negligible. This assumption is supported by the fact that the water temperature in the surface mixing layer, extending to ∼30 m depth, was shown to be nearly at the freezing point in this region from the expendable bathythermograph (XBT) and conductivity–temperature–depth (CTD) observations conducted during the cruise. We assumed snow depth is one-fifth of the ice thickness. This is based on observational results (Reference Toyota, Kawamura and WakatsuchiToyota and others, 2000). Longwave radiation flux was calculated from the empirical formula of Reference Maykut and ChurchMaykut and Church (1973). Calculation was started on 15 January when the sea-ice cover extended southward to the gridpoint, judging from the sea-ice concentration map of the Advanced Microwave Scanning Radiometer for Earth Observing System (AMSR-E), and was performed only during the night-time (21:00, 03:00 JST) because ice growth usually stops in the daytime due to abundant solar radiation. The estimated ice thickness evolution is shown in Figure 12a. Figure 12a predicts the ice thickness on 8 February as 16 cm, which approximately coincides with the thickness of the columnar ice layer of the sample (Fig. 11a). We confirmed that the error of the ERA-Interim dataset results in differences in the predicted ice thickness of ±1 cm. Therefore, we can safely regard as reasonable the growth rate profile predicted by the model (Fig. 12b).

Fig. 12. Results of thermodynamic model. (a) Thickness evolution predicted with ERA-Interim meteorological dataset. (b) Vertical profile of growth rate estimated from the model. (c) Effective fractionation coefficient derived by substituting the growth rate (b) with the empirical formula of Eqn (9).
Based on these datasets, we examine the applicability of the empirical formula, Eqn (9). The vertical profile of εeff, si calculated from Eqn (9) is shown in Figure 12c. To compare with the observed profile directly, the values averaged for each 5 cm depth from the bottom are superimposed in Figure 11b. Although εeff, si has detailed structure, Figure 11b indicates that overall the predicted εeff, si with Eqn (9) reproduced the observed profile well with an RMSE of 0.03‰. This result suggests that Eqn (9) is promising for correlating the observed vertical profile of εeff, si with the growth rate history for columnar ice.
Finally, we check the applicability of Eqn (10) by predicting the growth time from the δ18O profile. By estimating v i from the observed εeff, si in Figure 11b with Eqn (10), we can calculate how much time the ice took to grow for each layer (∼5 cm) except for the top snow-ice layer. By summing up the elapsed time, we can estimate the total number of days of growth before collection. As a result, 11.4 days was obtained. If we consider that the growth period is limited to night-time, the real period would be ∼23 days. This estimation shows that the growth period predicted by Eqn (10) almost coincides with the observed period of ice growth (24 days from 15 January to 8 February). Consequently, it is concluded that the empirical formulae, Eqns (9) and (10), are useful in revealing the growth rate history from the vertical δ18O profile of collected sea-ice samples.
7. Conclusion
In this study we examined the relationship between εeff, si and v i to apply the SBL model to real sea ice, focusing on columnar ice, and to improve understanding of the stable oxygen isotope fractionation process during the freezing of sea water through laboratory experiments and field observations. Our particular interest was in optimizing the parameters used in the model of Reference Eicken and JeffriesEicken (1998), which is based on the SBL model. Relatively low growth rates (v i < 1.7 × 10−7 m s−1) were covered by field observations in McMurdo Sound, Antarctica, while data for relatively high growth rates (v i > 2.2 × 10−7 m s−1) were obtained from the laboratory experiments. A case study on observational data from the southern Sea of Okhotsk supports the results.
In Antarctica, long-term monitoring observations allowed for the collection of ice samples and the measurement of growth rate data in the winters of 1999 and 2009. In the laboratory experiment, sea ice was grown in a tank under calm and steady conditions. Combining these datasets allowed evaluation of the relationship between εeff, si and v i for a wide range of growth rates for the first time. As a result, the optimum values of equilibrium pure-ice fractionation factor and boundary-layer thickness were estimated. We could not find a single set of parameter values that fit both the laboratory and field data, and the results show that the slope of the curve changed significantly for the growth rate of v i < 2.0 × 10−7 m s −1, and this change coincides with laboratory/field measurements. Therefore, different sets of physical parameters in the SBL model were estimated:

at the 95% confidence level. It was found that overall the model of Reference Eicken and JeffriesEicken (1998) tends to underestimate εeff, si, especially for v i > 2.0 × 10−7 m s −1 . The possible reason for the formation of these two regimes is that the relationship between v i and εeff, si is affected by various factors other than brine entrapment, such as grain size, ocean current and area enhancement due to groove structure at the bottom. Since the response depth required for adjustment to the change of v i was shown to be a few millimeters at most, it was confirmed that the vertical profile of εeff, si in sea ice corresponds approximately to the growth rate history of the sea ice.
For practical use, an empirical formula that correlates v i with εeff, si for the whole range of v i (0.8 × 10−7 < v i < 9.3 × 10−7 m s−1) was obtained.
where a 1 = 1.2280‰, b 1 = 0.7311‰, c 1 = 8.0100 × 10−8 m s−1, d 1 = 0.8441‰ and e 1 = 0.7800 × 10−6 m s−1. In the Sea of Okhotsk, an ice sample was collected in early February 2010 and the growth rates were estimated from the heat budget analysis. By applying this formula to a real sea-ice sample from the Sea of Okhotsk, it was shown that the εeff, si profile predicted from v i reproduced the observed profile well and that the δ18O profile is useful for estimating the growth rate history.
Thus the relationship between εeff, si and v i obtained from our study was revealed to be useful to climate research to some extent through the analysis of ice growth rate history. However, it should be noted that the analysis was focused on columnar ice. Observations show that whereas in the Arctic Ocean columnar ice prevails (e.g. Reference Gow, Tucker and WeeksGow and others, 1987), in a wide area of seasonal sea-ice zones frazil ice has been observed more frequently than columnar ice, for example in the Bellingshausen and Amundsen Seas (e.g. Reference Jeffries, Worby, Morris and WeeksJeffries and others, 1997), in the Weddell Sea (e.g. Reference Lange and EickenLange and Eicken, 1991) and in the Sea of Okhotsk (Reference Toyota, Takatsuji, Tateyama, Naoki and OhshimaToyota and others, 2007). Therefore, in order to apply the δ18O profile of sea ice to climate research in a wide range of regions, future study of the relationship between εeff, si and v i for frazil ice is required.
Acknowledgements
This research was supported by the FY 2011 Researcher Exchange Program between the Japan Society for the Promotion of Science and the Royal Society of New Zealand. We are sincerely grateful to the crew of P/V Soya of the Japan Coast Guard and our co-workers of the Institute of Low Temperature Science for their kind cooperation throughout the cruise in the Sea of Okhotsk. The measurement of δ18O for the laboratory experiment was done with the help of T. Nakatsuka. We thank Russell Frew and Dianne Clark of the Department of Chemistry isotope laboratory, University of Otago, for support and efforts in the isotope analysis and Joe Trodahl (Victoria University of Wellington) for providing access to the thermistor probe data used in this paper. Discussions with T. Kawamura, C. Haas, A. Sugimoto, D. Pringle, M. Kawai (Yamamoto) and G. Sazaki were very helpful. I.J.S. thanks Antarctica New Zealand for awarding her the 1999/2000 Antarctica New Zealand Sir Robin Irvine Postgraduate Scholarship, and the Foundation for Research Science and Technology, the University of Otago and the Blair Trust scholarship for financial support. Collection of the 2009 McMurdo Sound data was part of New Zealand’s contribution to the International Polar Year and was funded by the Foundation for Research Science and Technology, the University of Otago, Industrial Research Ltd and the National Institute of Water and Atmospheric Research Ltd. A.J.G. was supported by a University of Otago Postgraduate Scholarship. We thank Antarctica New Zealand for logistical support and Myles Thayer, Richard Sparrow and Peter Stroud for help constructing instruments. We thank Brian Staite and the Scott Base 2009 winter team for field support. Constructive comments by two anonymous reviewers are acknowledged.
















