Introduction
Taylor Dome (Fig. 1) is an ice dome located inland of the Transantarctic Mountains in south Victoria Land, East Antarctica. An ice core to bedrock was collected from near the summit of Taylor Dome in 1994 (Reference Grootes, Steig and StuiverGrootes and others, 1994). This core has provided a 150 kyr stable-isotope record (Reference SteigSteig and others, 2000; Reference Grootes, Steig, Stuiver, Waddington, Morse and NadeauGrootes and others, 2001) and an atmospheric CO2 record for the past 60 kyr (Reference Indermuhle, Monnin, Stauffer, Stocker and WahlenIndermuhle and others, 2000). Several short (<100m) firn cores were also collected in order to assess the spatial variability of climate and climate signal preservation in the area. One of these cores was collected approximately 30 km northeast of the main core site, at the head of Taylor Valley (Fig. 1), at a site that we call Taylor Mouth. Assuming the ice flow direction has not changed significantly in the Holocene, ice at the Taylor Mouth core site originated along a flowline from a saddle approximately 12 km to the northwest (Fig. 2).

Fig. 1. Taylor Dome study area. Solid dot marks the position of the 554 m Taylor Dome ice core, at elevation 2425 m; the surface-elevation contour interval is 50 m; box denotes Taylor Mouth study site (shown in Fig. 2); open dot marks Taylor Mouth core.

Fig. 2. Surface topography of Taylor Mouth area. Local coordinate system is based on an airborne radar survey described by D. Morse and others (unpublished information). Poles in strain grid (dots) were surveyed in several successive seasons to derive surface ice velocities (Morse and others, 2003); the flowline through the core site is inferred from these measurements. Stars mark locations of 10 m firn temperature measurements; core site is located at lower star (42.5 km, 11 km); shaded area in lower right is a nunatak.
The north side of Taylor Dome receives <4 cm ice equivalent accumulation per year (Reference MorseMorse and others, 1999). Consequently, the Taylor Mouth core, although only 100 m long, provides an isotope record spanning 2100 years (Waddington, unpublished data).
Although the two cores were collected only 30 km apart (Fig. 1), the Taylor Mouth and Taylor Dome oxygen isotope records show opposite trends in the late Holocene: Taylor Mouth becomes less negative towards the present, while Taylor Dome becomes more negative (Fig. 3). The other cores, collected within 2 km of the main Taylor Dome core, are isotopically similar to the Taylor Dome core.

Fig. 3. Two δ18O records from sites 30 km apart. The Taylor Dome record (a) and the Taylor Mouth record (b) are plotted on their own depth–age scales. Low-pass filtering with a cut-off at 1500 years produced the smooth dashed curves.
Because Taylor Mouth is a flank site, ice deeper in the core originated at higher, colder elevations. In this paper, we reject the idea that the trend in the Taylor Mouth core is due to spatial temperature variation following a standard δ18O–surface temperature relationship (e.g. Reference Dansgaard, Johnsen, Clausen and GundestrupDansgaard and others, 1973). Although other possible explanations may exist, we focus on two leading factors that could contribute to the observed differences between the two cores:
-
1. When compared to Taylor Dome, the Taylor Mouth area may receive varying percentages of accumulation from a wider variety of sources with distinct isotopic compositions. For example, precipitation at Taylor Mouth could come from storms passing over Taylor Dome, or from storms penetrating up Taylor Valley (Fig. 1). In addition, airborne or saltating snow could be blown from the polar plateau by the prevailing katabatic wind. Consequently, the Taylor Mouth isotope record may be more complicated than the Taylor Dome record.
-
2. Wind-driven ventilation of the firn near Taylor Mouth could modify stable-isotope ratios. Ventilation can redistribute and remove vapor in the firn, which causes modification of isotope ratios through sublimation and condensation, resulting in preferential loss of light isotopes. This process can be important in areas such as Taylor Mouth, where the accumulation rate is low, and snow remains near the surface, and within reach of ventilation for several years (Reference Waddington, Steig and NeumannWaddington and others, 2002).
Stable-Isotope Records
We have measured δ18O in the Taylor Mouth core. Using the depth–age model of Waddington (unpublished data), we can convert the measured δ18O(z) into a temporal record δ18O(t). We compare the Taylor Mouth isotope record with the Taylor Dome record. The oxygen isotope records for both cores were measured at the University of Washington Quaternary Isotope Laboratory;details of the measurement procedure are given by Reference Grootes, Steig, Stuiver, Waddington, Morse and NadeauGrootes and others (2001).
Figure 3a shows the stable-isotope record from Taylor Dome plotted on a time-scale based on measured firn compaction rates at Taylor Dome by Reference Hawley, Waddington, Morse, Dunbar and ZielinskiHawley and others (2002) for the most recent 1.3 kyr, and on matches of occluded gases with other well-dated cores by Reference MonninMonnin and others (2004) at earlier times. Figure 3b shows the Taylor Mouth stable-isotope record on its own depth–age scale (Waddington, unpublished data), which is based on a flow-band model that matches the depth and shape of an internal layer. In order to draw attention to the long-term trends evident in the records, we low-pass filtered both isotopic records to remove periods shorter than 1500 years (see bold dashed lines in Fig. 3).
The Taylor Dome δ18O record becomes progressively lighter in the late Holocene, showing an average decrease from –40‰ to –40.5‰ over the past 2100 years. In contrast, the Taylor Mouth δ18O becomes progressively heavier toward the present, increasing from –41 % to –38% . Spatial variation in the isotopic composition of precipitation and accumulation rate (‘deposition noise’) can result in uncorrelated isotopic records from adjacent cores (Reference Benoist, Jouzel, Lorius, Merlivat and PourchetBenoist and others 1982; Reference Fisher, Reeh and ClausenFisher and others, 1985; Reference JouzelJouzel and others, 1997; Neumann and others, 2004). At Dome C (accumulation rate ~4cmicea–1) Reference Benoist, Jouzel, Lorius, Merlivat and PourchetBenoist and others (1982) found that stable-isotope records from two cores collected <100 m apart were statistically correlated only for periods longer than about 500 years. In our case, the isotopic records from the Taylor Dome and Taylor Mouth cores remain uncorrelated after removing periods shorter than 1500 years.
Taylor Dome is a stable feature (Reference MorseMorse, 1997), with a relatively high net accumulation rate (~7.6cm ice a–1, Reference MorseMorse and others, 1999) compared with Taylor Mouth (Fig. 6a). Using internal-layer thickness data recorded by ice-penetrating radar, Reference Morse, Waddington and SteigMorse and others (1998) inferred that precipitation at Taylor Dome has come from the same direction over the past several thousand years. Therefore, we conclude that the Taylor Dome isotope record probably reflects changing local climate. This trend could result from gradual cooling in the late Holocene, from a slight elevation increase at the core site, from a shift in the transport pathway of precipitation to Taylor Dome, or from a change in the seasonality of precipitation (Reference Steig, Grootes and StuiverSteig and others, 1994). However, this climate trend is not evident in the Taylor Mouth record. This observation could be the result of non-climatic influences on the Taylor Mouth isotope record (which we explore here) or the manifestation of a substantially different climate at Taylor Mouth (e.g. Reference Waddington and MorseWaddington and Morse, 1994). However, due to the relatively short distance between the two cores (~30km), we assume that the sites experience similar changes in climate.
We subtract the trend of the Taylor Dome late-Holocene record (Fig. 3a), which we assume reflects only changing climate in the area (including Taylor Mouth), to remove the temporal climate signal from the Taylor Mouth record. This correction accentuates the trend in the Taylor Mouth record. The residual trend shown in Figure 4 must be due to processes other than climate change.
Isotope-Temperature Relation
Since both the Taylor Mouth and Taylor Dome core sites are higher than 1000ma.s.l., we might expect the annual average δ18O in this region to be correlated with mean annual temperature, as described by Reference Dansgaard, Johnsen, Clausen and GundestrupDansgaard and others (1973) and by other investigators. Sites that receive precipitation as a result of orographically induced cooling of storm systems may be expected to have a linear relationship between annual average δ18O values and mean annual temperature (Reference Dansgaard, Johnsen, Clausen and GundestrupDansgaard and others, 1973). Since the ice in the Taylor Mouth core was originally deposited over a range of elevation (Fig. 2), we might expect the stable-isotope record to include this elevation effect.
We use the same particle paths that provided ages for the Taylor Mouth core (Waddington, unpublished data) to calculate the elevation at the point of origin for ice at any depth in the core. These origin sites span 100 m vertically. Measured 10m firn temperatures at the two points marked by stars in Figure 2 indicate a surface temperature lapse rate of –2°C per 100 m elevation along the Taylor Mouth flowline. Since adiabatic cooling produces a lapse rate of –1°C per 100 m, the observed lapse rate suggests that other processes, such as isobaric cooling (Reference Grootes and StuiverGrootes and Stuiver, 1987) or katabatic effects, are also active at Taylor Mouth. The observed lapse rate together with the corrected δ18O trend in the core yields a temperature-isotope relationship of:
where T s is the mean annual surface temperature measured in degrees Celsius. In this analysis, we have made the critical assumption that the present slope of the δ18O-Ts relationship has been constant during the past 2100 years. Although Reference JouzelJouzel and others (1997) discuss several factors that can change this slope with time, we assume that this relationship has been stable over the period spanned by the Taylor Mouth core.
The slope of Equation (1) is significantly higher than other values reported for East Antarctica. Reference Dansgaard, Johnsen, Clausen and GundestrupDansgaard and others (1973) reported a slope of 0.76‰ per °C over a large range of surface temperatures in East Antarctica, while Reference Lorius, Merlivat, Jouzel and PourchetLorius and others (1979) reported a similar slope (0.75) for surface samples collected between Dome C and the coast. However, the variation in both surface temperature and surface δ18O values at Taylor Mouth is small compared with the range of values used by other studies, so the coefficients in Equation (1) are very poorly constrained. Consequently, it is unlikely that the entire trend in the residual of the Taylor Mouth ice core (Fig. 4) is due to advection by downslope ice flow and an orographically induced δ18O-Ts relationship.
Mixing of Snow from Different Sources
Most snow at Taylor Dome arrives as precipitation during storms from the south (Reference Morse, Waddington and SteigMorse and others, 1998). However, at Taylor Mouth several additional sources of accumulating snow could preclude a causal linear relationship between δ18O and Ts. Some precipitation could be delivered by storms as they pass over Taylor Dome. Without further orographic lifting, this snow would have a δ18O value comparable to, or perhaps slightly lighter than the summit snow. However, this source may be relatively unimportant, because Taylor Dome appears to create a precipitation shadow (Reference MorseMorse and others, 1999). Some precipitation may also occur with up-slope storm tracks from Taylor Valley; this snow may have a normal δ18O-Ts relationship given by (Reference Dansgaard, Johnsen, Clausen and GundestrupDansgaard and others, 1973):
The dominant wind direction at the Taylor Mouth core site is downslope, from Taylor Dome and the inland plateau (Fig. 1). Some accumulation at Taylor Mouth may be derived from wind-blown snow from Taylor Dome or the plateau having the isotopic signature of these higher-elevation source areas.
The distance that snow can be transported by wind is limited by sublimation of suspended grains. As described by Reference Déry and YauDéry and Yau (2001), sublimation rate is controlled by temperature, wind speed, relative humidity and energy input (sunlight and turbulence). For conditions at Taylor Mouth, order-of-magnitude estimates suggest that a characteristic distance for sublimation of blowing snow during wind transport is on the order of 30 km. Saltating grains could probably travel farther. These length scales are sufficient to allow isotopically light, plateau snow to reach Taylor Mouth, but not much farther.
We model accumulation at Taylor Mouth as a mixture of (a) up-valley orographically driven precipitation with δ18Ovalley(x) in Equation (2), and (b) blowing or saltating snow from the plateau or Dome, with uniform δ18O.
We define (x) as the decreasing fraction of the deposited snow that came from the polar plateau, as a function of x. We define δ18Oplateau as the isotopic value of that snow (treated as constant), δ18Ocore as the isotope record from the core after removing the temporal climate signal (Fig. 4), and δ18Ovalley(x) as Equation (2), using the measured Ts at Taylor Mouth. We represent the mixing of snow from these two sources (up-valley and plateau) by:
For a given δ18Oplateau and measured δ18Ocore, we vary the mixing ratio (x) to find a δ18Ovalley(x) that most closely matches Equation (2). Snow from Taylor Dome has an average δ18O of –40‰. Using this analysis, we find that snow from the summit of Taylor Dome cannot produce a δ18Ovalley(x) similar to Equation (2), regardless of the mixing ratio (x). In fact, any input snow that is isotopically heavier than the Taylor Mouth values from the base of the core (δ18O = –41.25‰, i.e. snow which accumulated close to the plateau, and may have a large fraction of wind-blown or saltated snow) generates a δ18Ovalley(x) with a larger slope than Equation (2). Measurements of δ18O from snow pits west of the Taylor Dome core site have average values of –45‰. Using δ18Oplateau = –45‰ is compatible with Equation (2), with mixing in which (x) = 0.45 at the upstream end of the flowline, and decreases linearly to (x) = 0 at the core site.
This analysis assumes the precipitation at Taylor Mouth arrives continually throughout the year. However, we know precipitation is episodic in both space and time (Reference McConnell, Bales and DavisMcConnell and others, 1997; Reference Van der Veen, Whillans and GowVan der Veen and others, 1999), and that δ18O values of precipitation reflect the season of deposition (Reference Steig, Grootes and StuiverSteig and others, 1994). Equation (3) uses annual average, rather than seasonally weighted, δ18O values. If snow is blown to Taylor Mouth from the plateau or Taylor Dome predominantly in one season, Equation (3) will not reflect this. For example, winter precipitation at Taylor Dome typically has δ18O = –45‰ (Reference Grootes and SteigGrootes and Steig, 1992), similar to the annual average δ18O of the plateau. Using this analysis, we are unable to distinguish between mixing snow from the plateau throughout the year and mixing snow from Taylor Dome only in winter.
This simple model illustrates two points: First, if the windblown snow deposited upstream of Taylor Mouth comprises only isotopically heavy snow from Taylor Dome (δ18O = –40‰) then an up-valley contribution of snow must have a very steep δ18O–Ts relationship. Second, a contribution of wind-blown snow from the plateau (δ18O = –45‰) is fully compatible with up-valley precipitation having a lower slope δ18O–Ts relationship, closer to what is seen elsewhere. We can explain the observed trend in the Taylor Mouth isotope record with this model if the source area for blown snow has a more negative δ18O value than the minimum Taylor Mouth values (δ18O = –41.25‰). In either case, the isotopic record from Taylor Mouth may not have a causal relationship with local temperature and is more complicated than the Taylor Dome record.
Post-Depositional Enrichment
Alternatively, the observed differences between the Taylor Mouth and Taylor Dome isotope records may result from post-depositional isotopic change at Taylor Mouth. Ice-core geochemistry, including stable isotopes, can be complicated by sublimation and redeposition of water within the upper few meters of the snowpack (Reference McConnell, Bales, Stewart, Thompson, Albert and RamosMcConnell and others, 1998; Reference Wagnon, Delmas and LegrandWagnon and others, 1999). Wind-driven ventilation increases the rate of water-vapor exchange in near-surface firn (Reference AlbertAlbert, 2002). Because these processes are most active in the uppermost few decimeters, a key predictor of the degree of post-depositional change is the length of time that snow remains in the near-surface. Therefore, we expect postdepositional enrichment to be most intense in areas of lowest accumulation rate, because that snow can undergo near-surface water-vapor exchange for several years (Wad-dington and others, 1996, 2002).
Reference Grootes and SteigGrootes and Steig (1992) measured δ18O in the upper 2 m at sites on a 10 km grid on Taylor Dome. The average isotopic values change from –42.7‰ along the south side of the dome where the accumulation rate is highest, to –41 ‰ at the summit, to –39.2‰ along the north side of the dome where the accumulation rate is lowest. Although it is possible that such differences in mean isotopic composition on relatively small spatial scales could be due to deposition processes, we also examine the possibility of postdepositional causes. Gradients of vapor pressure in firn can cause sublimation and redeposition; one commonly observed result is depth hoar. As noted by several authors (e.g. Reference Stichler, Schotterer, Fröhlich, Ginot, Kull and Gäggeler.Stichler and others, 2001), the formation of depth hoar causes isotopic change in firn. In fact, the snow pits along the north side of Taylor Dome showed extensive metamorphism and depth hoar formation along with isotopic enrichment (Reference Grootes and SteigGrootes and Steig, 1992). Two of the pits sampled by Reference Grootes and SteigGrootes and Steig (1992) showed greater isotopic enrichment than seen in the average pit data. Here, we investigate fractionation processes in the firn, and estimate the importance of firn ventilation on sublimation and redeposition rates, and explore post-depositional changes of stable-isotope ratios at Taylor Mouth.
Conventional models of isotopic diffusion in firn (e.g. Reference Whillans and GrootesWhillans and Grootes, 1985; Reference Cuffey and SteigCuffey and Steig, 1998) treat the firn as a closed system. Consequently, those models cannot produce a net isotopic change. A mechanism for removing light isotopes, such as isotopic exchange between the firn and the overlying atmosphere, is required if the isotopic trend seen in the Taylor Mouth core is due to postdepositional change. Reference Grootes and SteigGrootes and Steig (1992) suggested the isotopic enrichment observed along the north side of Taylor Dome may be caused by mass loss during firn metamorphism. Our model allows for isotopic exchange between the firn and the atmosphere through ventilation, i.e. airflow driven by pressure gradients (Reference ColbeckColbeck, 1989).
Model description
We assume that water vapor sublimates from ice with negligible isotopic fractionation, i.e. δ18Osubl = δ18Oice (Reference Friedman, Benson, Gleason, Taylor, O’Neill and KaplanFriedman and others, 1991). This assumption implies that sublimation is sufficiently rapid that the characteristic time to evaporate the quasi-liquid surface layer described by Reference HobbsHobbs (1974) and other investigators is shorter than the time for that layer to equilibrate isotopically with the underlying solid ice surface.
As vapor recondenses, the heavier isotope 18O is redeposited preferentially. Since the redeposited ice is isotopically heavier than the vapor from which it condenses, the remaining vapor is depleted in the heavy isotope. If we consider this as a Rayleigh process, we can quantify how the δ18O of the remaining vapor and the condensate change as a function of the amount of vapor remaining. In a Rayleigh process, the condensate forms at isotopic equilibrium with the vapor, and is immediately removed after condensation. Following Reference DansgaardDansgaard (1961):

where R v is the stable-isotope ratio in the vapor, R vo is its initial value, α is the temperature-dependent fractionation coefficient (e.g. Reference MajoubeMajoube, 1971), β is the fraction of vapor that has not condensed in the firn (i.e. the fraction of vapor remaining) and Rc is the average isotopic ratio of the total condensate. (See Appendix for details.) Using the above relations, we construct an analytical model of δ18O changes in a mass of firn as a result of airflow through the firn.
Reference Massey and GrootesMassey and Grootes (1991, Reference Massey and Grootes1992) studied the isotopic composition of water vapor above the snowpack–air interface at Summit, Greenland. The δ18O of the atmospheric water vapor (δ18O = –45‰) was approximately in isotopic equilibrium (Reference MajoubeMajoube, 1971) with the average δ18O of the snowpack (δ18O = –30‰). Reference Massey and GrootesMassey and Grootes (1992) forced this atmospheric vapor through 2 m of firn. By comparing the δ18O of the atmospheric vapor with the δ18O of the vapor that had been pumped through the snowpack, they found that the pumped vapor was a mixture of atmospheric vapor and vapor sublimated directly from the average snow grains.
Guided by this result, we model the pore-space vapor as a mix of vapor with the δ18O of atmospheric vapor (which is in isotopic equilibrium with the snow) and vapor sublimated from the firn with the δ18O of the snowpack. We assume that the air in the snowpack pore space is always at the saturation vapor density. The total mass mv of vapor in the pore space in a reference volume of firn is then constant (concentration of moles x pore-space volume × molar mass of water).
We let τ specify the characteristic residence time for air in firn. We define S as the fractional rate at which the remaining mass of firn sublimates. The fraction of the firn that sublimates per characteristic time is then Sτ . We again let β specify the fraction of the pore-space vapor that does not condense. The fraction (1 – β) of the pore-space vapor is therefore redeposited in the firn. The fraction of the pore-space vapor that is derived from sublimating snow grains is determined by the relative humidity H of the atmosphere. If H of the incoming air is close to unity (100%), then the fraction of the pore-space vapor that comes from sublimating snow grains is small. Conversely, if the H of the incoming air is low, then the fraction of pore-space vapor derived from sublimating snow grains is large. Consequently, the fraction of the firn Sτ that sublimates per τ is limited by the H of the air entering the firn.
Values of S are determined by the vapor density of air entering the firn, the saturation vapor density (determined by firn temperature) and the pore-space volume of the firn (determined by firn porosity). We assume that the time required for the pore-space air to reach saturation vapor density is small relative to the characteristic time τ an assumption addressed below. Consequently, the air in the pore spaces is always at saturation vapor density.
Using these parameters, we can calculate how the net solid mass of firn mf in a reference volume changes as a function of time, how the isotopic content of the condensate δ18Oc changes as a function of time, and how the bulk isotopic content δ18Of of the remaining firn changes with time.
We non-dimensionalize both mass terms (mass of firn mf and mass of vapor in pore space mv in a reference volume) by the mass of a reference volume (see Appendix for details):


where



δ18Ovo(f) is the isotopic composition of the pore-space vapor, α, b and Fare constants, β is defined above and α is the vapor-to-solid equilibrium isotopic fractionation coefficient. Although we derived this model for δ18O, we can also predict changes of δD in the firn by using the appropriate fractionation coefficient.
Discussion of assumptions
First, we assume that vapor condensation proceeds as a Rayleigh process. Reference Jouzel and MerlivatJouzel and Merlivat (1984) also explored an isotopic kinetic effect, based on the different diffusivities of heavy and light species of water in air. This difference is important in clouds, where the relative humidity (H) can exceed saturation. This additional fractionation factor modifies the fractionation coefficient α in the snowpack, where H is close to unity, by at most 4% and is not considered here.
Second, we assume that the average isotopic content of the vapor sublimated from the firn equals the average isotopic content of the firn, i.e. the molecules in the remaining snow grain are continuously well mixed. There are a number of processes that act to isotopically homogenize grains in the snowpack. Reference Whillans and GrootesWhillans and Grootes (1985) examined isotopic diffusion through solid ice grains. They found that the diffusion time-scale for isotopic perturbations within the grain to decay to half amplitude was:

where l is the path length from the interior of the grain to the air–ice interface, Dice is the temperature-dependent diffu-sivity of stable isotopes in ice (Reference HobbsHobbs, 1974, p. 379), and 0.057 is a geometric factor. Summer temperatures at Taylor Dome are typically –20°C. For a spherical grain of radius 0.25 mm, this diffusion time-scale is about 20days. In the winter, when the temperature is much lower, the diffusion time-scale is about 100 days. In addition, several grain-metamorphism processes will homogenize the remaining mass isotopically, as smaller grains are consumed and incorporated into larger grains;here we discuss two of them. (1) The differences in the radius of curvature of snow grains result in local differences in saturation vapor pressure (e.g. Reference Colbeck and ColbeckColbeck, 1980). At –40°C (the mean annual temperature at Taylor Dome), the time-scale for radius-of-curvature metamorphism (Reference Colbeck and ColbeckColbeck, 1980) ranges from 20min for small grains (radius = 1 μm) to decades for large grains (radius = 1 mm). (2) Temperature gradients in the snow also cause vapor-pressure gradients, which lead to grain metamorphism (Reference ColbeckColbeck, 1983). At –40°C and a temperature gradient of 5°Cm–1 per meter, the time-scale for grain consumption varies from 18 hours for small grains (radius = 1 μm) to 2 years for large grains (radius = 1 mm).
Clearly, diffusion within the grains acts to homogenize the grains isotopically more quickly than the above grain-metamorphism processes for an average grain-size of 100μm. We treat the grains as isotopically well mixed, an assumption that may be valid only in the summer season.
Third, we assume that α, mv, S, H and β are constant with respect to time. The fractionation coefficient α is an exponential function of temperature, which changes throughout the year. During the 30°C amplitude of the annual cycle at Taylor Dome, α varies from 1.014 to 1.018 (Reference MajoubeMajoube, 1971); in the results presented here, we use a value of 1.016, which corresponds to about –40°C.
S and β vary with the relative humidity, H, of the air entering the snowpack. When air enters the firn with H~ 1, the firn sublimation rate S will be low, since the air cannot hold much more vapor. Conversely, air entering with H < 1 results in a higher value for S. We assume that the time required for pore-space vapor to reach saturation density is much shorter than the residence time τ of air in the firn (Reference NeumannNeumann, 2003). Reference Massey and GrootesMassey and Grootes (1992) found that at Summit, Greenland, in 1990, the mixing ratio between vapor from the atmosphere and vapor from sublimating snow grains was 0.5–0.25. This suggests that the atmospheric relative humidity at the time of the study was 0.5– 0.75. Recent measurements of relative humidity at South Pole (personal communication from S. Warren, 2001) also fall in this range.
Furthermore, both mv and S will vary as the remaining mass of the firn, mf, and the porosity change with time. Our expression for the change in mass of firn (Equation (6)) is therefore only valid for small changes in the mass of firn. We also note that since changes in mf over time are small, the factor of exp[Sŕ(1 – Fa)] is the dominant time-dependent factor in Equation (8).
Our model also assumes that the firn is isothermal. Since saturation vapor density is a function of temperature, the temperature profile of the firn is important. Several authors (e.g. Reference Grootes and StuiverGrootes and Stuiver, 1997; Reference Stichler, Schotterer, Fröhlich, Ginot, Kull and Gäggeler.Stichler and others, 2001) have noted that diurnal temperature variation can induce vapor exchange between surface snow and the atmosphere due to the daily cycle of saturation vapor density of the firn. A model that accounts for variable temperature and the associated variation in saturation vapor density along a trajectory (e.g. Reference Albert and McGilvary.Albert and McGilvary, 1992), and through time, will be an important component of the full solution. The numerical model of Reference Neumann and WaddingtonNeumann and Waddington (2004) incorporated variable temperature and is a next step toward a physically based model of isotopic changes in firn.
This analysis does not include a full treatment of other physical processes in the firn. We have not explicitly calculated the time required for mass exchange from the ice crystals to the vapor, or airflow rates through the firn. The residence time, τ, of air in the firn depends on the physical properties of the firn such as surface microtopography and permeability (Reference Waddington, Cunningham, Harder, Wolff and BalesWaddington and others, 1996). These properties may change throughout the year, leading to variations in τ. Our model uses a constant τ. The ratio of the characteristic time for the mass exchange between phases to the characteristic residence time of air in the firn will determine to what extent saturation vapor density is reached as air moves through the firn, and whether isotopic equilibrium is reached between the vapor in the pore space and in the surrounding snow grains. Consequently, better understanding of the time-scale for mass exchange from ice grains to vapor will be another important part of a more complete solution in the future. Our analysis assumes that the air in the pore spaces is always saturated, and that the pore-space vapor can leave the firn before reaching isotopic equilibrium with the snow grains.
Model application
To estimate an upper limit for S, the fractional rate of snow mass sublimation, we consider the limiting case where all the pore-space vapor originates from sublimated ice grains (i.e. air enters firn with H = 0). We first estimate the saturation vapor density in the pore space using the Clausius–Clapeyron equation (Reference ColbeckColbeck, 1990):

where ρvo and T0 are reference vapor density and temperature (usually taken at the triple point), and T is absolute temperature. This formulation ignores the vapor density dependence on radius of curvature of snow grains. However, for average grain-sizes in snow (r = 100–1000 μm), the bulk temperature dominates the local saturation vapor density (Colbeck, 1982).
Surface snow at Taylor Dome has porosity on the order of 0.5–0.6 m3 of void space per m3 of snow. This leads to a total mass of vapor in the pore space of 10–4 kg of vapor per m3 of snow, or about 10–6 kg of vapor per kg of snow. This is the upper limit on the fraction Sτ of the firn that can be sublimated per characteristic time τ. Based on the ventilation modelling of Reference ColbeckColbeck (1989) and Reference Waddington, Cunningham, Harder, Wolff and BalesWaddington and others (1996), we expect τ will be on the order of 10 s for the upper 50cm of firn. These estimates result in an upper estimate of S (i.e. Smax) on the order of 10–7s–1, which is reached if the H of air entering the firn is zero.
In our model, air entering the firn typically has H > 0 and has some initial isotopic composition, which then mixes with vapor sublimated from the firn. Although H and S are independent parameters in our equations, physically we can link these parameters. If we assume that saturation vapor density in the firn cannot be exceeded, then S = (1 – H) x Smax. For example, for H = 0, we assume that all pore-space vapor is due to sublimating ice grains, and S takes its maximum value.
The parameter β, which defines the fraction of vapor lost to the atmosphere, is also poorly known. Reference Albert and McGilvary.Albert and McGilvary (1992) demonstrated that for moderate airflow speeds, air can exit firn with some super- or sub-saturation (on the order of 1%). By using a range of β, we study a range of both sub- and super-saturation of air leaving the firn. In this model, as β goes to zero, the relative humidity of air leaving the firn goes to zero, and all pore-space vapor is condensed in the firn.
Our model predictions of post-depositional isotopic change, using Equation (8), and given the above assumptions, are presented in Figure 5 for a range of (S,β) combinations. The horizontal axis represents a range of mass vaporization rates from a minimum of S = 0 (no sublimation) to Smax (all pore-space vapor due to sublimation). The vertical axis represents a range of possible β values, from a minimum of 0 (no vapor lost to atmosphere – all vapor is condensed in the firn) to a maximum of 1 (all vapor lost to atmosphere – no vapor is condensed in the firn).

Fig. 5. Change in bulk δ18O of idealized polar snow after 1 year, in units of ‰, for a range of β (fraction of vapor leaving the firn) and ST (fraction of firn sublimated in time τ). Contour interval is 0.25‰. Our models show that it is possible to either enrich or deplete heavy isotopes in the firn. With additional environmental information at a site, such as the temperature of the firn as a function of depth and time of year, this model can be used to predict patterns of post-depositional change.
We verify that this model behaves as expected for a few limiting cases. For β = 1, all pore-space vapor is lost to the atmosphere, and no vapor is condensed in the snowpack. Since there is no condensation, and therefore no isotopic fractionation, we expect that the average δ18O value of the snowpack will not change, regardless of the mass vaporization rate, S, since vapor is sublimated from snow grains, and does not recondense before leaving the firn. As Figure 5 shows, along the horizontal line β = 1, our model predicts that there is no change in δ18O of the firn, as expected.
If all the pore-space vapor is derived from sublimating snow grains, then S = Smax. If all of this vapor recondenses in the snowpack (β = 0), then we again expect that the average δ18O value of the snow will not change. This situation occurs in the lower right corner of Figure 5. As expected, the model predicts no change in δ18O.
Finally, if no snow sublimates (S = 0), and sub-saturated air leaves (β < 1), then atmospheric vapor is deposited in the snow. Atmospheric vapor is assumed to be in equilibrium with the snow, and therefore to be more negative than the snow. This situation, while not likely to be widespread in nature, would lead to a decrease in the bulk δ18O of the firn, as seen in the lower left corner of Figure 5.
Figure 5 allows us to explore many different environmental scenarios. If the relative humidity of air exiting the snowpack is approximately equal to the relative humidity of air entering the snowpack, then solutions are found near the diagonal from the upper left corner to the lower right corner. Furthermore, we anticipate that atmospheric relative humidity H will be greater than 50%, which corresponds to β > 0.5.
Figure 5 shows that, for a range of β, after 1 year the average isotopic content of the snowpack could change by a few tenths of 1 ‰. Even for very low S = 0.1 x Smax = 10–8 (corresponding to atmospheric H = 0.9), our model predicts a change of 0.05‰ after 1 year. For S = 0.3, Smax = 3 × 10–8 (corresponding to H = 0.7), our model predicts a change of 0.2‰ after 1 year. At Taylor Mouth, the net accumulation rate is low, as shown in Figure 6a. Firn remains near the surface, within reach of ventilation, for ~5 years or longer near the core site. Even though the post-depositional isotopic change proceeds slowly, the total offset could be as much as several per mil at Taylor Mouth.

Fig. 6. (a) Net accumulation-rate pattern along the Taylor Mouth flowline from Waddington (unpublished data). (b) Isochrones and particle paths to the core site. (c) δ18O below the ventilation zone along the flowline. Solid curve shows values tracked from core site using ice-flow model; dotted curve shows best fit if variation is due entirely to mixing of plateau snow (with fixed δ18O) and orographic precipitation from Taylor Valley (δ18O linearly related to surface temperature); dashed curve shows best fit if variation is due to post-depositional change that scales with accumulation rate. Since accumulation rate decreases upstream of x = 3.5 km, postdepositional processes would lead to enhanced enrichment there.
In general, we expect the magnitude of the ultimate isotopic change to scale inversely with accumulation rate. Although vapor exchange can occur down to the pore close- off depth, most water-vapor exchange occurs in the upper few decimeters of the firn, as a result of the large temperature gradients induced there by the diurnal temperature cycle (Reference AlbertAlbert, 2002). Instead of calculating the transient temperature and water-vapor pressure fields directly, our model assumes isothermal snow and prescribes the rate of water-vapor exchange. High accumulation rates bury surface snow before post-depositional isotope fractionation can significantly modify the δ18O values of the deposited snow. Conversely, low accumulation rates allow snow to remain near the surface, where it can be subjected to this process for several years. The general effect of this process is to remove the lighter isotope preferentially. Isotope values in the firn become higher (less negative) through time.
The accumulation rate along the Taylor Mouth flowline (see Fig. 6a) varies from a low of ~4cm ice equivalent a–1 near the core site, to a high of ~11 cm ice equivalent a–1 at 8 km upstream along the flowline. Consequently, we expect post-depositional modification to vary along the flowline. We can estimate the pattern of isotopic enrichment below the ventilation zone (i.e. ≈2 m depth) by scaling expected isotopic enrichment inversely with accumulation rate.
Using the flowlines in Figure 6b to match the ice in the Taylor Mouth core with accumulation rates (Fig. 6a) at the corresponding surface-origin sites, we can predict how postdepositional isotopic alteration varies with depth in the core. Ice that originated near the core site, where the accumulation rate is low, experienced the largest post-depositional modification. This ice may have been several per mil more negative when first deposited. Conversely, ice from deeper in the core originated farther up the flowline where the accumulation rate is higher; this ice experienced less post-depositional modification. Since the effect of this modification is to make δ18O values less negative (i.e. heavier) the surface snow along the flowline may have had a more uniform stable-isotope distribution when it was first deposited.
We can explain some of the residual trend in the Taylor Mouth δ18O record (Fig. 4) with this model of postdepositional isotopic enrichment. Based on our calculations, it is relatively easy to change the isotopic composition of surface snow by several per mil prior to deep burial at Taylor Mouth. The sign of the change will depend on poorly constrained factors, such as the relative humidity of the atmosphere above the snow surface and the isotopic composition of water vapor in the atmosphere. As shown in Figure 5, it is possible to either enrich or deplete the firn of heavy isotopes. If the firn temperature is lower than the air temperature, we may expect air leaving the firn to be subsaturated relative to the air, due to the temperature sensitivity of saturation vapor density (Equation (14)). This situation may result in a net transport of atmospheric vapor into the firn, and a corresponding decrease in the δ18O value of the firn. Conversely, if the firn is warmer than the atmosphere, air may leave the firn with some degree of super-saturation. The net result of this situation may be to remove water vapor from the firn into the atmosphere, and enrich the remaining firn in heavy isotopes.
In order to make a quantitative prediction about postdepositional changes in near-surface snow (upper 1 m), the firn evolution model should be coupled with models for other physical processes. We expect changes in firn temperature and vapor density on both diurnal and annual time-scales to be important components of vapor exchange between the firn and the atmosphere. Modelling the temperature of the firn as a function of depth and time, and investigating the time-scale for transfer of water molecules from the solid to the vapor phase will both be important. By using our equations with a two-dimensional model which solves the coupled equations of energy conservation and water-vapor movement (e.g. Reference AlbertAlbert, 2002; Reference Neumann and WaddingtonNeumann and Waddington, 2004) we will be better able to predict the pattern of post-depositional isotopic change with depth in the snowpack.
Our model suggests that isotope profiles from low-accumulation-rate areas (such as the north side of Taylor Dome) will show isotopic enrichment relative to areas with a higher accumulation rate. Other investigators have shown similar results. Assuming the initial isotopic composition of the snow, Reference Satake and KawadaSatake and Kawada (1997) used a Rayleigh model to determine that as much as 35% of precipitation was sublimated prior to deep burial in east Dronning Maud Land, Antarctica, leading to an isotopic enrichment of 6‰ for δ18O and 50‰ for δD. Their study site has a very low accumulation rate, with snow remaining near the surface (upper 1 m) for as long as 40 years. Our more detailed model supports the findings of Reference Satake and KawadaSatake and Kawada (1997), and further demonstrates the importance of understanding postdepositional changes in areas of low accumulation rate.
Discussion
The residual trend in the Taylor Mouth stable-isotope record (Fig. 4) is unlikely to result wholly from an orographically driven Dansgaard δ18O–Ts relationship similar to Equation (2). Further measurements may make it possible to differentiate between our two preferred remaining causes, i.e. mixing of isotopically distinct accumulation from at least two sources, and spatially variable post-depositional isotopic change. A combination of both processes is also possible.
If precipitation at Taylor Mouth is a mix of snow from different sources, we would expect surface snow to vary monotonically from isotopically heavy (reflecting an up- valley component to precipitation) at Taylor Mouth, to isotopically light (reflecting a polar-plateau source) near the topographic saddle (Fig. 2), as shown by the dotted curve in Figure 6c.
Alternatively, we expect the degree of post-depositional change to increase with decreasing accumulation rate. Ice at the bottom of the core (100 m depth) originates in an area of relatively high accumulation rate (Fig. 6a);snow deposited at this point should be modified least by post-depositional change. Several kilometers upstream, toward the nearby saddle (Fig. 2), the accumulation rate is again low. Snow deposited close to the saddle would have experienced more post-depositional modification, and should therefore have a heavier isotopic signature, than snow deposited farther downstream where the accumulation rate is higher. The dashed curve in Figure 6c shows the predicted variation in δ18O along the flowline if the variations seen in the core are due entirely to post-depositional changes.
Samples collected along the length of the flowline, from several meters depth, i.e. below the ventilated zone, could distinguish between these two options. A profile intermediate between the dotted and dashed curves in Figure 6c would suggest that both processes are active. These tests could also be carried out by sampling a longer core from the Taylor Mouth site.
In addition, measuring isotopic enrichment between the surface snow and snow at several meters depth could also quantify the degree of post-depositional change. However, depositional noise could make these data difficult to interpret. Recent measurements by Reference Neumann and WaddingtonNeumann and others (2004) at six sites in Antarctica showed that horizontal variability in δ18O (or δD) on a scale of 1 m in snow pits can be as large as, or larger than, the seasonal isotopic variation. Consequently, a single isotope profile may not be representative of a site. This uncertainty can be reduced by directly measuring the isotopic deposition noise at a site (e.g. Reference Neumann and WaddingtonNeumann and others, 2004), or by collecting replicate profiles.
Our results suggest that post-depositional processes could complicate the interpretation of stable-isotope records from low-accumulation-rate areas, where snow remains in the upper meter for several years. Records from relatively high-accumulation areas (e.g. much of West Antarctica) are probably only minimally influenced by these processes. In order to assess the importance of post-depositional isotopic change at other ice-core sites, estimates (or measurements) of key physical properties of the firn (microstructure, porosity, grain-size) and atmospheric variables (temperature, wind speed, relative humidity, isotopic content of the atmosphere) are required. In addition, replicate sampling to determine the small- and regional-scale isotopic variation should be conducted. Prior work (Reference JouzelJouzel and others, 1997) suggests that accumulation rate is the most important factor in small-scale isotopic variation, although more recent work (Reference Neumann and WaddingtonNeumann and others, 2004) demonstrates that significant meter-scale spatial variation is possible at relatively high (~10cm ice equivalent a–1) accumulation-rate sites.
Conclusions
Interpretation of the stable-isotope record from the Taylor Mouth ice core is non-unique, given the available data. However, we can comment on several possible complicating factors. First, the record is probably affected by snow accumulation arriving from multiple sources, including: snow blown from Taylor Dome and from the plateau surface inland of Taylor Dome, and snow precipitated from storms passing over the summit of Taylor Dome;and precipitation from storms coming up-slope from Taylor Valley. Only the last of these might be expected to show a conventional δ18O–Ts relationship. Second, the record may also be influenced by post-depositional modification of stable-isotope ratios as a result of near-surface ventilation (upper 1 m). We predict a post-depositional enrichment trend opposite to the trend in accumulation rate. Further measurements of stable-isotope ratios at the surface along the flowline to the core site would help to differentiate between these possibilities. The large accumulation-rate gradient across Taylor Dome makes it an attractive site for further study of post-depositional geochemical changes. The International Trans-Antarctic Scientific Expedition (ITASE) program (e.g. Reference Mayewski and GoodwinMayewski and Goodwin, 1997) explores spatial patterns of Antarctic climate by analyzing arrays of ice cores collected over large areas. However, in areas of low accumulation rate, this increased spatial sampling will lead to correctly inferred spatial climate patterns only when postdepositional processes are understood.
Acknowledgements
We thank Antarctic Support Associates for field support, and fellow participants in the Taylor Dome project for collecting data presented here. Discussions with K.M. Cuffey are appreciated. Comments by D. Wagenbach, an anonymous reviewer and scientific editor B. Hubbard have produced many improvements in the paper. This work was supported by US National Science Foundation grants OPP-8915924, OPP-9421644, OPP-0229416 and University of Washington Royalty Research Fund grant RRF-2503.
Appendix: Model for Post-Depositional Change
We can create closed-form solutions to predict the evolution of the remaining solid mass of firn mv (t) in a reference volume, the isotopic content of the condensate δ18Oc(f), and the bulk isotopic content of the remaining firn δ18Of(f). We begin with the equations of Dansgaard (1961) for condensation of vapor over an ice surface:
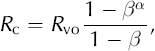
where R denotes the ratio of 18O to 16O in a sample of water, and the subscript refers to the type of sample. In this nomenclature R v denotes the ratio in water vapor, R c is the ratio in the condensate and R vo is the initial ratio in the vapor, β is the fraction of the initial mass of vapor remaining and α is a temperature-dependent fractionation coefficient (e.g. Dansgaard and others, 1973). Since isotopic composition is more commonly expressed on the δ18O scale, we convert Equations (A1) and (A2) to this scale. The δ18O of a sample is defined as:

where the standard is commonly Standard Mean Ocean Water (SMOW). We can manipulate Equation (A3) to find:

We use Equations (A2) and (A3) to find an expression for δ18Oc (Equation (7)):
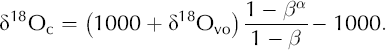
We model the pore-space vapor as a mix of atmospheric vapor, which we assume is in isotopic equilibrium with the average δ18O of the snowpack, and vapor derived locally through grain sublimation. The mixing ratio between these two sources is (1 - H), and the equation for δ18Ovo is Equation (9).
We now construct a model for the changes in remaining firn mass mf and isotopic content δ18Ovo, with time. By dividing the remaining firn mass, mf, by the mass of a reference volume, we non-dimensionalize the expressions involving mass. If we assume the time required for mass exchange between the solid and vapor phases in the firn (i.e. the mass-exchange time-scale) is short relative to the residence time of air in the firn, τ, then the normalized mass of firn decreases by the fraction S τin time τ, where S is the fractional rate at which the firn sublimates. The mass also increases due to redeposition. We assume air in the snowpack is always saturated. The normalized mass of vapor in the pore space of a reference volume is mv. The amount of mass redeposited in time τ is (1 - β)mv, and the remaining mass of the firn mf (t) in a reference volume changes through time as:
Assuming that the temporal derivative of mf can be approximated as:
Equation (A6) can be written as a first-order differential equation for mf(t):
The characteristic residence time of air in the firn, τ, is a function of depth (Reference ColbeckColbeck, 1989), though in this analysis, we treat it as constant. A closed-form solution for m f (Equation (6)) follows after integration.
The δ18O of the remaining firn (δ18Of) is a weighted average of the δ18O of the condensate and the δ18O of the remaining mass:

Substituting Equations (A5) and (9) into (A9), we get a differential equation for the isotopic content, δ18Of, of the remaining firn:

where F α and b are defined in Equations (10), (11) and (12). The solution to this first-order linear ordinary differential equation is presented as Equation (8).
Given appropriate choices for β and S, these equations can be used to calculate the changes in an idealized firn sample as a function of time. The assumptions made in this analysis are discussed in the text.









