List of Symbols
. List of Symbols

Introduction
Current estimates of global mean sea-level rise by 2100 span an order of magnitude from 0.2 to 2.0 m (e.g. Reference Willis and ChurchWillis and Church, 2012), and the greatest source of uncertainty in these predictions is the contribution from the Antarctic and Greenland ice sheets (e.g. Reference GregoryGregory and others, 2013). The poor constraints on ice-sheet mass loss exist due to (1) inadequate numerical descriptions within models of ice dynamic processes including deformation, fracture and sliding, and (2) uncertainty in ice-sheet boundary conditions including bedrock topography and lithological heterogeneity, grounding line location and geothermal flux (e.g. Reference Alley and JoughinAlley and Joughin, 2012; Reference GregoryGregory and others, 2013; Reference Vaughan and StockerVaughan and others, 2013; Reference Carson, McLaren, Roberts, Boger and BlankenshipCarson and others, 2014). The recent development of high- or variable-resolution ice-sheet models that solve the full system of Stokes equations describing the three-dimensional state of stress within an ice mass, or higher-order approximations to the full-Stokes equations, has led to an improved capability to simulate the dynamics of ice streams, ice shelves and outlet glaciers (e.g. Reference PattynPattyn and others, 2008; Reference Morlighem, Rignot, Seroussi, Larour, Ben Dhia and AubryMorlighem and others, 2010; Reference Gillet-ChauletGillet-Chaulet and others, 2012; Reference Seddik, Greve, Zwinger, Gillet-Chaulet and GagliardiniSeddik and others, 2012; Reference GagliardiniGagliardini and others, 2013).
In addition to the numerical scheme used to determine stress distribution within an ice mass, a crucial component of an ice-sheet model is the description of ice flow properties, which relates the flow rates to the stresses driving ice deformation. The flow relation most commonly used to describe the rheology of polycrystalline ice is the creep power law of Reference GlenGlen (1958),
where ![]() and
S
are the second-order strain-rate and deviatoric stress tensors respectively, and A(T) is a temperature-dependent flow parameter. The effective shear stress,
and
S
are the second-order strain-rate and deviatoric stress tensors respectively, and A(T) is a temperature-dependent flow parameter. The effective shear stress, ![]() (we use Einstein’s summation convention unless explicitly stated otherwise), is a function of the scalar second invariant of
S
(Reference NyeNye, 1957), and the stress exponent is typically taken as n = 3 (Reference Budd and JackaBudd and Jacka, 1989; Reference Cuffey and PatersonCuffey and Paterson, 2010).
(we use Einstein’s summation convention unless explicitly stated otherwise), is a function of the scalar second invariant of
S
(Reference NyeNye, 1957), and the stress exponent is typically taken as n = 3 (Reference Budd and JackaBudd and Jacka, 1989; Reference Cuffey and PatersonCuffey and Paterson, 2010).
Equation (1) was empirically derived from secondary (minimum) creep rates (Reference GlenGlen, 1955) on polycrystalline samples with an initially random distribution of c-axis orientations. Under conditions of constant stress and temperature, secondary creep occurs transiently at strains of ∼0.5–2%. At this point no significant changes to crystal size and orientation have occurred, and the bulk properties of samples with initially random c-axis orientations, including their rheology, remain isotropic (Reference Budd and JackaBudd and Jacka, 1989). Consequently, the Reference GlenGlen (1958) flow relation is isotropic and does not adequately describe the anisotropic rheology typical of the high-strain creep deformation that predominates within polar ice masses.
Terrestrial ice occurs in the low-pressure hexagonal Ih phase, and single crystals exhibit a high level of viscoplastic anisotropy due to the considerably lower resistance to slip on crystallographic basal planes compared with non-basal slip systems (e.g. Reference KambKamb, 1961; Reference Duval, Ashby and AndermanDuval and others, 1983; Reference Trickett, Baker and PradhanTrickett and others, 2000a). Turning to polycrystalline ice deformation, numerous laboratory and field observations indicate how microstructure evolves as a function of strain (e.g. Reference Gow and WilliamsonGow and Williamson, 1976; Reference Russell-Head and BuddRussell-Head and Budd, 1979; Reference Gao and JackaGao and Jacka, 1987; Reference Pimienta, Duval and LipenkovPimienta and others, 1987; Reference Budd and JackaBudd and Jacka, 1989; Reference Tison, Thorsteinsson, Lorrain and KipfstuhlTison and others, 1994; Reference DurandDurand and others, 2007; Reference Gow and MeeseGow and Meese, 2007; Reference MontagnatMontagnat and others, 2014a). A conspicuous feature of this evolution is the development of patterns of preferred c-axis orientations (fabrics), which through the anisotropy of single crystals engender a flow-induced polycrystalline anisotropy that influences large-scale ice-sheet dynamics. Laboratory ice-deformation experiments indicate how the polycrystalline anisotropy observed during tertiary creep (at strains ≥10%) is associated with enhanced flow rates relative to the secondary (minimum) creep rates. Furthermore, the strain rates, fabric and distribution of grain sizes (texture) are influenced by the flow configuration, stress magnitude and temperature (e.g. Reference LileLile, 1978; Reference Budd and JackaBudd and Jacka, 1989). Tertiary creep rates for unconfined compression are about three times greater than Reference GlenGlen (1958) estimates determined for isotropic ice under similar conditions of stress magnitude and temperature, while simple shear tertiary creep rates are a factor of about three times greater still (e.g. Reference Treverrow, Budd, Jacka and WarnerTreverrow and others, 2012; Reference Budd, Warner, Jacka, Li and TreverrowBudd and others, 2013).
A flow relation for ice-sheet modelling should provide a realistic description of anisotropic rheology while limiting the introduction of complexity that reduces computational efficiency and potentially restricts model resolution. Despite not adequately describing the observed anisotropic rheology of polycrystalline ice, the Reference GlenGlen (1958) flow relation remains widely used in large-scale simulations due to its simplicity and a lack of suitable alternatives. A common means of incorporating a simple representation of flow enhancement into models using the Reference GlenGlen (1958) relation is through a constant multiplying factor (e.g. Reference CalovCalov and others, 2010), sometimes referred to as a flow enhancement factor. Since the observed magnitude of flow enhancement varies according to the stress configuration, values ranging from ∼3 to 12 may be used depending on the chosen reference (e.g. Reference Budd and JackaBudd and Jacka, 1989; Reference Cuffey and PatersonCuffey and Paterson, 2010, ch. 3.4.7). Simulations of Antarctic ice-sheet evolution by Reference Golledge, Fogwill, Mackintosh and BuckleyGolledge and others (2012) demonstrate the sensitivity of predicted ice-sheet geometries to the value of the Reference GlenGlen (1958) flow relation enhancement factor.
Various anisotropic flow relations for polycrystalline ice have been proposed over recent decades and two broad approaches to their development can be identified. In the first, the flow is derived from consideration of grain-scale deformation (and possibly recrystallization and recovery) processes. The approaches taken vary in complexity due to the deformation processes considered and the manner in which the applied stresses are distributed onto individual grains (e.g. Reference LileLile, 1978; Reference Van der Veen and WhillansVan der Veen and Whillans, 1994; Reference Svendsen and HutterSvendsen and Hutter, 1996; Reference Morland and StaroszczykMorland and Staroszczyk, 2003; Reference Gillet-Chaulet, Gagliardini, Meyssonnier, Montagnat and CastelnauGillet-Chaulet and others, 2005; Reference FariaFaria, 2006; Reference Placidi, Greve, Seddik and FariaPlacidi and others, 2010). Where the deformation of individual grains is explicitly derived from their crystallographic orientation relative to the applied stresses, the bulk (polycrystalline) response is obtained via integration (or homogenization) of the individual grain responses (e.g. Reference Azuma and Goto-AzumaAzuma and Goto-Azuma, 1996; Reference ThorsteinssonThorsteinsson, 2002). For such relations, forward modelling requires a fabric evolution scheme, which adds numerical complexity that precludes their use in continental-scale ice-sheet models.
The second, more pragmatic, approach is to base the description of anisotropy on a parameterization of key rheological variables, such as the stress configuration or crystal c-axis orientation effects (e.g. Reference Wang and WarnerWang and Warner, 1999; Reference Wang, Warner and BuddWang and others, 2002; Reference Pettit and WaddingtonPettit and Waddington, 2003; Reference Budd, Warner, Jacka, Li and TreverrowBudd and others, 2013). Various perspectives and additional detail on anisotropic flow relation development can be found in reviews by Reference MarshallMarshall (2005), Reference Placidi, Hutter and FariaPlacidi and others (2006), Reference Gagliardini, Gillet-Chaulet, Montagnat and HondohGagliardini and others (2009) and Reference MontagnatMontagnat and others (2014b).
In this work we compare the predictions of four anisotropic flow relations using data from the Dome Summit South (DSS) ice-coring site at Law Dome, East Antarctica. Using a combination of ice-core, borehole and surface measurements the vertical distribution of stresses driving flow at the coring site is predicted. For brevity, acronyms are used to identify the flow relations investigated in the following, and usage of their associated citations is implied in each case. For the Reference Azuma and Goto-AzumaAzuma and Goto-Azuma (1996) flow relation we use AGA. The flow relation of Reference ThorsteinssonThorsteinsson (2002) incorporates a parameterization of nearest-neighbour grain interactions, so we adopt the acronym TNNI. Reference Placidi, Greve, Seddik and FariaPlacidi and others (2010) describe a Continuum mechanical Anisotropic Flow model based on an anisotropic Flow Enhancement factor and we adopt their acronym, CAFFE. For the Reference Budd, Warner, Jacka, Li and TreverrowBudd and others (2013) flow relation we use B2013.
Methods
Ice-core and borehole site input data
Temporally sequential measurements of borehole inclination, from which the vertical profile of the horizontal velocity is obtained, are a valuable adjunct to the ice-core and borehole data streams routinely obtained during deep drilling of ice cores for palaeoclimate records. The combined datasets are ideally suited to evaluating the dynamics of ice masses. Here we use data from the DSS ice core, drilled 4.7 km south-southwest of the Law Dome summit in East Antarctica (Fig. 1), to evaluate the AGA, TNNI, CAFFE and B2013 flow relations. For each relation we calculate depth profiles of the shear stress, aligned parallel to the surface flow direction, and the vertical compression deviatoric stress. Input data include strain rates derived from the borehole inclination; ice-core c-axis orientation fabrics; borehole temperatures; and surface measurements of the drill-site ice flow direction, velocity and strain rate (Fig. 2; Table 1). To assist assessment of the DSS-site stress estimates we use strain-rate and fabric data from laboratory ice deformation experiments (Reference Budd, Warner, Jacka, Li and TreverrowBudd and others, 2013) to calculate the corresponding applied stresses; unlike the stresses in an ice sheet, the applied stresses in laboratory experiments are known.
Table 1. DSS borehole site and ice-core information (Reference Morgan, Wookey, Li, Van Ommen, Skinner and FitzpatrickMorgan and others, 1997, Reference Morgan, Van Ommen, Elcheikh and Li1998)


Fig. 1. Location of the Dome Summit South (DSS) ice-core site (yellow star) at an elevation of 1370 m on Law Dome, East Antarctica (see inset). The red box indicates a 25 km × 25 km region surrounding the Law Dome summit. Within this region the blue line is a portion of the flowline which extends from the dome summit through the DSS ice-coring site and downstream towards Vanderford Glacier. The background image is from the Landsat Image Mosaic of Antarctica (Reference BindschadlerBindschadler and others, 2008); 100 m elevation contours are from Reference Bamber, Gomez-Dans and GriggsBamber and others (2009).

Fig. 2. DSS ice-core and borehole data as a function of ice equivalent depth. Bedrock is estimated to occur at an ice equivalent depth of 1198.5 ± 20 m. (a) Borehole temperature (Reference Morgan, Van Ommen, Elcheikh and LiMorgan and others, 1998). (b) Shear strain rate, derived from borehole inclination measurements projected onto the direction parallel to the drill-site surface flow direction (Reference Morgan, Van Ommen, Elcheikh and LiMorgan and others, 1998). The smoothed shear strain-rate profile (bold black line) is a five-point running mean. The vertical strain rate is derived from the horizontal velocity profile and surface accumulation rate using Eqn (3). (c) Orientation tensor eigenvalues, ai , were determined from the c-axis vector distributions measured for each of 185 thin sections obtained from the DSS ice core (Reference LiLi, 1995; Reference Morgan, Wookey, Li, Van Ommen, Skinner and FitzpatrickMorgan and others, 1997). The triplets of points at each depth are the eigenvalues, ai , of the second-order orientation tensor, where a 1 > a 2 > a 3. The bold lines represent eigenvalues determined from fivemember composite fabrics, typically containing N ≈ 500 individual c-axes.
In the following we present ice-core and borehole data as a function of ice equivalent depth,
where ρ(χ) is the firn/ice density at actual depth χ, ρ
ice = 917 kg m−3 is the ice density and ![]() is the total ice-sheet thickness. Below the firn–ice transition at ∼40 m the ice equivalent depth has a constant offset of −21.5 m relative to the actual depth (Reference Van Ommen, Morgan and CurranVan Ommen and others, 2004; Reference RobertsRoberts and others, 2015).
is the total ice-sheet thickness. Below the firn–ice transition at ∼40 m the ice equivalent depth has a constant offset of −21.5 m relative to the actual depth (Reference Van Ommen, Morgan and CurranVan Ommen and others, 2004; Reference RobertsRoberts and others, 2015).
Borehole and surface measurements
Figure 2a shows how ice temperature at DSS increases from a mean annual surface value of −21.8 C to −6.9 C at the bottom of the borehole. The DSS core was drilled to near bedrock, and small fragments of rock were recovered from the lowest core section. Comparison of the borehole depth (1195.6 m) and estimates of the total ice thickness based on radio-echo sounding (RES; 1220 ± 20 m (Reference Morgan, Wookey, Li, Van Ommen, Skinner and FitzpatrickMorgan and others, 1997)) suggest bedrock was <45 m below the bottom of the borehole. From this it may reasonably be assumed that the basal ice temperature is less than the in situ pressure-melting point, despite the relatively high geothermal flux of 72 mW m−2 at the DSS site (Reference Van Ommen, Morgan, Jacka, Woon and ElcheikhVan Ommen and others, 1999).
Figure 2b (grey line) shows the shear strain-rate profile derived from the borehole inclination projected onto a plane parallel to the ice surface velocity vector of 2.04 ± 0.11 m a−1 at 225 ± 3°, determined from 4 months of GPS measurements during the 1995/96 austral summer (Reference Morgan, Van Ommen, Elcheikh and LiMorgan and others, 1998). The small-scale fluctuations and negative values of the shear strain rate at depths above 300 m are a consequence of noise in the inclination data where deformation rates are low (Reference Morgan, Van Ommen, Elcheikh and LiMorgan and others, 1998). The borehole movement and hence shear strain rate in the direction transverse to the surface flow (not shown) has a similar magnitude to the total measurement error and is considered negligible (Morgan and others,1998). The surface strain-rate components are (3.22 ± 0.016) × 10−4 a−1 in the line of flow and (4.50 ± 0.027) × 10−4 a−1 transverse to the surface flow direction (Reference Morgan, Van Ommen, Elcheikh and LiMorgan and others, 1998). We specify a coordinate system at the DSS site where z is the vertical (upward) direction with x and y, respectively, parallel and transverse to the surface flow direction.
The shear strain rate does not increase monotonically to the bed; a broad maximum occurs at ∼1000 m depth, or ∼180 m above bedrock (Fig. 2b). The transition to lower shear strain rates below ∼1000 m is not accompanied by any corresponding large-scale changes in ice chemistry or soluble-impurity content, rather it is associated with stress relaxation towards the bed due to flow over undulating bedrock topography at Law Dome (e.g. Reference Budd and JackaBudd and Jacka, 1989; Reference Morgan, Wookey, Li, Van Ommen, Skinner and FitzpatrickMorgan and others, 1997). Similar maxima in the shear strain rate ∼130 m above the bed have been observed in the BHF, BHC-1 and BHC-2 boreholes drilled at near-coastal sites along a flowline from Law Dome summit towards Cape Folger (Reference Russell-Head and BuddRussell-Head and Budd, 1979; Reference EtheridgeEtheridge, 1989), where the ice thickness is ∼300–385 m. Modelling indicates that these peak shear strain rates are associated with a corresponding maximum in the shear stress and that the onset of a transition to lower shear strain rates (and stresses) with depth is related to the magnitude of the bedrock undulations.
Superimposed on the decreasing shear strain rate at depths below 1000 m is a narrow band between 1110 and 1124 m where the shear rate is about five times greater than that in ice immediately above and below (Fig. 2b). The ice-core δ18O record indicates this ice was deposited during the Last Glacial Maximum (LGM) and compared with the overlying Holocene ice has (1) significantly smaller mean grain area, (2) a strong vertical single-maximum crystal orientation fabric and (3) particle concentrations two orders of magnitude higher (Reference Morgan, Van Ommen, Elcheikh and LiMorgan and others, 1998). Reference Li, Jacka and MorganLi and others (1998) have shown that the higher insoluble impurity concentrations associated with this layer are sufficient to retard rates of microstructural evolution. Unlike the ice immediately above and below, this allows the vertical single-maximum pattern of c-axis orientations, which originated upstream of the DSS site, to persist within this narrow band of ice. This high level of polycrystalline anisotropy, combined with higher temperatures closer to the bed, results in a discrete band from 1100 to 1124 m with the highest shear strain rates within the DSS borehole (Fig. 2b).
Vertical strain rates
The vertical strain-rate profile, ![]() (Fig. 2b), was not determined by direct measurement and is obtained from Eqn (3) assuming steady-state conditions and ice incompressibility (e.g. Reference ReehReeh, 1988):
(Fig. 2b), was not determined by direct measurement and is obtained from Eqn (3) assuming steady-state conditions and ice incompressibility (e.g. Reference ReehReeh, 1988):
where ![]() is the annual accumulation rate,
is the annual accumulation rate, ![]() is the mean of the horizontal velocity depth profile, u(z), z
T is the ice thickness, and the horizontal velocity shape function ψ(z) relates u(z) to
is the mean of the horizontal velocity depth profile, u(z), z
T is the ice thickness, and the horizontal velocity shape function ψ(z) relates u(z) to ![]() as described below. Assuming that ψ(z) only varies gradually along the line of flow,
as described below. Assuming that ψ(z) only varies gradually along the line of flow,

and the last term in Eqn (3) can be neglected. As the surface slope at the DSS site is low (α ∼ 0.0051), the second term in Eqn (3) is also negligible since ![]() is about two orders of magnitude greater than
is about two orders of magnitude greater than ![]() (Table 1). The assumption that Law Dome is in steady state and has a stable geometry is reasonable since the DSS ice-core isotope and chemistry records indicate a stable annual accumulation rate over the past ∼6.8 ka (Reference Van Ommen, Morgan and CurranVan Ommen and others, 2004). It follows that the vertical strain rate can be estimated from the first term in Eqn (3).
(Table 1). The assumption that Law Dome is in steady state and has a stable geometry is reasonable since the DSS ice-core isotope and chemistry records indicate a stable annual accumulation rate over the past ∼6.8 ka (Reference Van Ommen, Morgan and CurranVan Ommen and others, 2004). It follows that the vertical strain rate can be estimated from the first term in Eqn (3).
The near-surface (75.6 m actual depth) vertical strain rate of ![]() , which was derived from the bore-hole inclination data, agrees favourably with the independently determined surface GPS value of
, which was derived from the bore-hole inclination data, agrees favourably with the independently determined surface GPS value of ![]() (Table 1; Reference Morgan, Van Ommen, Elcheikh and LiMorgan and others, 1998).
(Table 1; Reference Morgan, Van Ommen, Elcheikh and LiMorgan and others, 1998).
Ice-core measurements
The DSS ice-core fabric data used in this study include c-axis orientations from 185 thin sections obtained at ∼6m intervals between 117 m depth and the bottom of the ice core (Fig. 2c; Reference LiLi, 1995; Reference Morgan, Van Ommen, Elcheikh and LiMorgan and others, 1998). All fabrics were measured manually at the time of drilling using a Rigsby stage, with each fabric typically restricted to N ≈ 100 individual c-axis orientations due to the laborious nature of the measurement procedure (Reference Morgan, Wookey, Li, Van Ommen, Skinner and FitzpatrickMorgan and others, 1997). For certain sections, mainly at depths below ∼1040 m, the number of grains within an individual fabric was <100 due to the combined effects of higher temperatures and stress relaxation on grain growth, leading to higher mean grain sizes and a reduction in the total number of grains within a single thin section.
Following Reference WoodcockWoodcock (1977), the eigenvalues ai (i = 1, 2, 3) of the normalized second-order c-axis orientation tensor,

are used to illustrate fabric evolution with depth at DSS (Fig. 2c).
The eigenvalues of Λ are related as a
1 + a
2 + a
3 = 1, where by convention 0 ≤ a
3 ≤ a
2 ≤ a
1 ≤ 1. Because the eigenvalues describe the degree of clustering of c-axis orientations about their respective eigenvectors they are related to the fabric shape. The eigenvector, ![]() , of the maximum eigenvalue, a
1, is the direction about which the distribution of orientations is minimized, whilst
, of the maximum eigenvalue, a
1, is the direction about which the distribution of orientations is minimized, whilst ![]() is the direction about which the distribution is largest. As a
1 → 1, the distribution of orientations becomes smaller, i.e. fabrics become stronger or more concentrated. It follows for an isotropic (random) distribution of orientations that
is the direction about which the distribution is largest. As a
1 → 1, the distribution of orientations becomes smaller, i.e. fabrics become stronger or more concentrated. It follows for an isotropic (random) distribution of orientations that ![]() . The area of individual grains was not determined during orientation measurements (Reference LiLi, 1995), so volume weighting of the orientation data (e.g. Reference Durand, Gagliardini, Thorsteinsson, Svensson, Kipfstuhl and Dahl-JensenDurand and others, 2006) was not possible and all orientations contribute equally to (Fig. 2c).
. The area of individual grains was not determined during orientation measurements (Reference LiLi, 1995), so volume weighting of the orientation data (e.g. Reference Durand, Gagliardini, Thorsteinsson, Svensson, Kipfstuhl and Dahl-JensenDurand and others, 2006) was not possible and all orientations contribute equally to (Fig. 2c).
Several general comments can be made regarding the DSS ice core c-axis distribution:
-
1. Near-surface fabrics are not isotropic because a 1 ≫ a 2 ≈ a 3. Non-random patterns of orientations near the firn-to-ice transition are most likely influenced by a range of factors related to accumulation, grain growth and deformation processes.
-
2. All fabrics down to ∼1000 m are vertically clustered, with
 approximately parallel to the long axis of the core. The strength of the single-maximum fabrics increases with depth from 550 m to 1000 m. These fabrics are consistent with the increasingly high shear strain rates over the same depth range. Small-scale fluctuations in fabric strength (Fig. 2c) are closely coupled to changes in the grain size, with smaller grain sizes associated with stronger fabrics (Reference Morgan, Wookey, Li, Van Ommen, Skinner and FitzpatrickMorgan and others, 1997).
approximately parallel to the long axis of the core. The strength of the single-maximum fabrics increases with depth from 550 m to 1000 m. These fabrics are consistent with the increasingly high shear strain rates over the same depth range. Small-scale fluctuations in fabric strength (Fig. 2c) are closely coupled to changes in the grain size, with smaller grain sizes associated with stronger fabrics (Reference Morgan, Wookey, Li, Van Ommen, Skinner and FitzpatrickMorgan and others, 1997). -
3. Down to ∼1000 m, fabrics are approximately transversely isotropic. Based on the surface flow divergence, indicated by
 (Table 1), the consistent difference of ∼0.04 between a
2 and a
3 may be related to some transverse spreading of the fabrics; however, the azimuthal orientation of thin sections is not available to confirm this.
(Table 1), the consistent difference of ∼0.04 between a
2 and a
3 may be related to some transverse spreading of the fabrics; however, the azimuthal orientation of thin sections is not available to confirm this. -
4. Below ∼1040 m multiple-maxima fabrics are observed. These are consistent with topographically induced stress relaxation and increasing ice temperatures at depth resulting in recrystallization, including significant grain growth (Reference LiLi, 1995; Reference Morgan, Wookey, Li, Van Ommen, Skinner and FitzpatrickMorgan and others, 1997). Multiple-maxima fabrics are not well described by the orientation tensor eigenvalues; however, a reduction in a 1 and an increase in the difference between a 2 and a 3 below ∼1040 m are indicative of a transition from the single-maximum fabrics associated with the overlying high shear zone.
Background to the flow relations
The AGA, TNNI and CAFFE flow relations have been selected for comparison with the B2013 flow relation because each differs in the degree to which physically based interpretations of grain-scale deformation and recovery processes are incorporated into the formulation. These flow relations may be broadly classified as homogenization schemes since the strain-rate response of a polycrystalline aggregate is based on consideration of the orientation relationship between individual grains (represented by crystallographic c-axis vectors) and the macroscopic deviatoric stress tensor. Both the AGA and TNNI relations define the stress acting on an individual grain in terms of its c-axis orientation relative to the applied stress in conjunction with a consideration of neighbour grain orientation effects. The CAFFE flow relation is a generalization of the Reference GlenGlen (1958) flow relation using grain orientations in conjunction with the deviatoric stress tensor to specify a scalar anisotropic enhancement factor. The B2013 relation is an empirical parameterization based on deformation experiments conducted in a range of stress configurations using laboratory-made ice.
Several other anisotropic flow relations could have been considered for inclusion in this study (e.g. Reference LileLile, 1984; Reference Van der Veen and WhillansVan der Veen and Whillans, 1994; Reference Svendsen and HutterSvendsen and Hutter, 1996; Reference Gagliardini and MeyssonnierGagliardini and Meyssonnier, 2000; Reference GödertGödert, 2003; Reference StaroszczykStaroszczyk, 2003; Reference Gillet-Chaulet, Gagliardini, Meyssonnier, Montagnat and CastelnauGillet-Chaulet and others, 2005; Reference PettitPettit and others, 2011; Reference Martín, Gudmundsson and KingMartín and others, 2014). In many anisotropic flow relations, fabrics are represented by a c-axis orientation distribution function (ODF). For some flow relations (such as CAFFE) it is possible to also work directly with discrete c-axis vectors instead of an ODF. For other flow relations it is not straightforward to make the translation to a vector description of the c-axis distribution. For reasons of simplicity, a constrained form of ODF, where the anisotropy is described by a limited number of variables, is often specified. This can introduce symmetry limitations on the ODF (e.g. a restriction to only transversely isotropic orientation patterns), with the result that naturally occurring fabrics that do not satisfy these criteria are not adequately described. Since a specific aim of this study is to compare the empirical B2013 relation to microscale flow relations using the DSS ice-core crystal orientation fabric data, we have restricted our analysis to a subset of candidate flow relations where the deforming polycrystalline aggregate can be described by a discrete distribution of c-axis orientation vectors.
AGA flow relation
In the AGA flow relation individual grains are assumed to deform only by glide on crystallographic basal planes, normal to the c-axis. The outer product of the basal glide direction, m , and the crystallographic c-axis vectors, c , define a geometrical factor tensor G (g) for a grain,
G (g) is the origin of anisotropy in the AGA relation and describes the geometric connection between the applied stress tensor on a grain, σ (g), and the scalar magnitude of the resolved shear stress, τ (g), on the basal plane of a grain:
where X : Y denotes the generalized inner product X ij Y ji . Because grains are assumed to deform by basal glide alone, the temperature-dependent flow parameter, βS , for easy glide of single crystals is used in the definition of the strainrate tensor for a grain (Reference Azuma and Goto-AzumaAzuma and Goto-Azuma, 1996):
where ![]() is the symmetrization of
G
and
is the symmetrization of
G
and
Here ![]() is a material-dependent parameter, specific to single-crystal deformation, which is several orders of magnitude higher than corresponding values for polycrystalline ice deformation (e.g. Reference Cuffey and PatersonCuffey and Paterson, 2010, ch. 3.4).
is a material-dependent parameter, specific to single-crystal deformation, which is several orders of magnitude higher than corresponding values for polycrystalline ice deformation (e.g. Reference Cuffey and PatersonCuffey and Paterson, 2010, ch. 3.4). ![]() is largely determined by the concentration of soluble and insoluble impurities (e.g. Reference Jones and GlenJones and Glen, 1969; Reference Trickett, Baker and PradhanTrickett and others, 2000b), Q
s is a single-crystal creep activation energy and R is the universal gas constant. Equation (8) includes the single-crystal creep power-law stress exponent, n, and from the derivation of Reference Azuma and Goto-AzumaAzuma and Goto-Azuma (1996) this value should apply in Eqn (8) and later in Eqn (11). Based on Reference WeertmanWeertman (1983), Reference Azuma and Goto-AzumaAzuma and Goto-Azuma (1996) assume n = 3 for single crystal deformation. Analyses of single-crystal deformation by Reference Duval, Ashby and AndermanDuval and others (1983) and Reference TreverrowTreverrow (2009) demonstrate that a stress exponent of n = 2 is appropriate for easy glide of single crystals, suggesting that this value should have featured in the AGA relation. For consistency with the flow relation presented by Reference Azuma and Goto-AzumaAzuma and Goto-Azuma (1996), and the other relations considered in this study, we use the more widely accepted value of n = 3 for polycrystalline deformation.
is largely determined by the concentration of soluble and insoluble impurities (e.g. Reference Jones and GlenJones and Glen, 1969; Reference Trickett, Baker and PradhanTrickett and others, 2000b), Q
s is a single-crystal creep activation energy and R is the universal gas constant. Equation (8) includes the single-crystal creep power-law stress exponent, n, and from the derivation of Reference Azuma and Goto-AzumaAzuma and Goto-Azuma (1996) this value should apply in Eqn (8) and later in Eqn (11). Based on Reference WeertmanWeertman (1983), Reference Azuma and Goto-AzumaAzuma and Goto-Azuma (1996) assume n = 3 for single crystal deformation. Analyses of single-crystal deformation by Reference Duval, Ashby and AndermanDuval and others (1983) and Reference TreverrowTreverrow (2009) demonstrate that a stress exponent of n = 2 is appropriate for easy glide of single crystals, suggesting that this value should have featured in the AGA relation. For consistency with the flow relation presented by Reference Azuma and Goto-AzumaAzuma and Goto-Azuma (1996), and the other relations considered in this study, we use the more widely accepted value of n = 3 for polycrystalline deformation.
Reference Azuma and Goto-AzumaAzuma and Goto-Azuma (1996) proposed an empirical relationship for σ (g) as a function of the macroscopic stress tensor, σ , and the c-axis orientation of the grain and its nearest neighbours, based on experimental observations of polycrystalline ice deformation (Reference AzumaAzuma, 1995). This relationship, along with the assumptions

where N T is the number of grains in a polycrystalline aggregate, defines the macroscopic strain rate,
Thus the macroscopic anisotropy of the AGA relation is determined by the arithmetic mean of G
(g) for each grain. The assumptions leading to Eqn (10) are significant since they enable expressions for the redistribution of the applied stress on each grain, based on neighbour grain c-axis orientations, to be eliminated from the calculation of ![]() . This greatly simplifies numerical implementation of the AGA flow relation as c-axis data only enter into the calculation of
G
.
. This greatly simplifies numerical implementation of the AGA flow relation as c-axis data only enter into the calculation of
G
.
TNNI flow relation
Similar to the AGA flow relation, in the TNNI flow relation individual grains are assumed to deform only by glide on basal planes and the polycrystalline strain rate is determined from the homogenization of individual grain deformations. Of the flow relations considered in this study, the TNNI relation incorporates the most physically motivated description of grain-scale deformation processes. The deformation of individual grains is based on the slip rate for each crystallographic basal slip system and includes a parameterization of c-axis dependent nearest-neighbour grain interactions.
The anisotropy of the TNNI flow relation is derived from the Schmid tensor, R s , for each basal slip system within a grain,
where
c
is the crystallographic c-axis vector,
b
s
is the Burgers vector, parallel to the crystallographic slip direction, and the index s = 1, 2, 3 denotes quantities associated with each a-axis slip system within a grain. The Schmid tensor links the macroscopic stress,
σ
, to the shear stress, ![]() , resolved onto the basal plane of each grain,
, resolved onto the basal plane of each grain,

The quantity, ![]() , is analogous to τ
(g) in the AGA flow relation, Eqn (7). Reference ThorsteinssonThorsteinsson (2002) defined a parameterization of grain interaction that influences the magnitude of anisotropic flow enhancement in the TNNI flow relation. The softness parameter for a grain,
, is analogous to τ
(g) in the AGA flow relation, Eqn (7). Reference ThorsteinssonThorsteinsson (2002) defined a parameterization of grain interaction that influences the magnitude of anisotropic flow enhancement in the TNNI flow relation. The softness parameter for a grain,

is a function of the resolved shear stresses on a reference grain, ![]() , and each of its six nearest neighbours,
, and each of its six nearest neighbours, ![]() . The grain interaction parameters for the reference grain, C
0, and each of its nearest neighbours, C
n, define the extent to which neighbour grain interactions influence the redistribution of applied stresses onto each grain. Reference ThorsteinssonThorsteinsson (2002) specifies three levels of nearest-neighbour grain interaction (NNI):
. The grain interaction parameters for the reference grain, C
0, and each of its nearest neighbours, C
n, define the extent to which neighbour grain interactions influence the redistribution of applied stresses onto each grain. Reference ThorsteinssonThorsteinsson (2002) specifies three levels of nearest-neighbour grain interaction (NNI):
-
1. No NNI. C 0 = 1 and C n = 0. No neighbour grain interaction,
 , corresponding to a homogeneous stress condition.
, corresponding to a homogeneous stress condition. -
2. Intermediate NNI. C 0 = 6 and C n = 1. The relative contribution of the reference grain to
 is equivalent to that of all the neighbour grains combined.
is equivalent to that of all the neighbour grains combined. -
3. Full NNI. C 0 = 1 and C n = 1. The relative contribution of all grains to
 is equivalent.
is equivalent.
Full NNI produces the highest levels of anisotropic flow enhancement and is used in the following analyses.
The velocity gradient tensor, L (g), of a single crystal is the sum of the velocity gradient tensor for each slip system,
where the temperature dependent term,
is that specified in the Reference GlenGlen (1958) flow relation, Eqn (1). Q is an activation energy for the creep of polycrystalline ice and R and T are as previously defined. The pre-exponential term A 0 can be determined empirically from the secondary creep of isotropic polycrystalline ice and is assumed to be dependent upon material-specific factors including ice density and the size and concentration of soluble and insoluble impurities (e.g. Reference Budd and JackaBudd and Jacka, 1989; Reference Cuffey and PatersonCuffey and Paterson, 2010). The constant B (Eqn (15)) is an arbitrary tuning parameter that ensures the flow relation reproduces physically-accurate strain rates (Reference ThorsteinssonThorsteinsson, 2001). The macroscopic velocity gradient, L, for a polycrystalline aggregate of N T grains is the arithmetic mean of the individual grain velocity gradients (Reference ThorsteinssonThorsteinsson, 2002):

and the polycrystalline strain rate is
CAFFE flow relation
In the CAFFE flow relation, individual grains are also assumed to deform by basal glide; however, unlike the AGA and TNNI flow relations the polycrystalline strain rate is not derived from a homogenization of individual grain deformations. The magnitude of the applied deviatoric stress S resolved on the basal plane of a grain is used to define a deformability index, D( c ), for each grain, which quantifies the proportion of the applied stress able to drive deformation of a grain specified by its c-axis vector, c.
where St
is the magnitude of the resolved basal deviatoric stress component. An array of c-axis vectors can be described by an orientation distribution function (ODF) that quantifies the volume fraction of c-axis orientations. By integrating the single crystal deformability, D(
c
), weighted by the ODF over the unit sphere, ![]() , the polycrystalline deformability D is obtained (Reference Seddik, Greve, Placidi, Hamann and GagliardiniSeddik and others, 2008; Reference Placidi, Greve, Seddik and FariaPlacidi and others, 2010). By expressing integrals as summations over the N
T individual crystals in a polycrystalline aggregate, the macroscopic deformability, D, can also be determined directly,
, the polycrystalline deformability D is obtained (Reference Seddik, Greve, Placidi, Hamann and GagliardiniSeddik and others, 2008; Reference Placidi, Greve, Seddik and FariaPlacidi and others, 2010). By expressing integrals as summations over the N
T individual crystals in a polycrystalline aggregate, the macroscopic deformability, D, can also be determined directly,

The macroscopic deformability is used to determine a nonlinear, scalar enhancement function, E(D), for the Reference GlenGlen (1958) flow relation in Eqn (1). E(D) is defined over the interval ![]() ,
,

where E min and E max are user-defined limits of enhancement, such that E(D) has the following fixed points:
-
1. D = 0, E(0) = E min. The minimum enhancement value is returned when there is no resolved shear stress on the basal planes of grains. To avoid numerical issues Reference Placidi, Greve, Seddik and FariaPlacidi and others (2010) recommend selecting 0 < E min < 0.1.
-
2. D = 1, E(1) = 1. The factor of
 in Eqn (19) ensures that D = 1 for an isotropic c-axis distribution, resulting in an enhancement of E = 1. In this situation the CAFFE flow relation, Eqn (22), reduces to the Reference GlenGlen (1958) flow relation.
in Eqn (19) ensures that D = 1 for an isotropic c-axis distribution, resulting in an enhancement of E = 1. In this situation the CAFFE flow relation, Eqn (22), reduces to the Reference GlenGlen (1958) flow relation. -
3.
 . The maximum deformability returns the theoretical maximum enhancement, Emax, when the applied stress is entirely resolved onto the basal planes of all grains. This corresponds to an idealized scenario where all grains in a polycrystalline aggregate have identical c-axis orientations that are normal to an applied simple shear stress.
. The maximum deformability returns the theoretical maximum enhancement, Emax, when the applied stress is entirely resolved onto the basal planes of all grains. This corresponds to an idealized scenario where all grains in a polycrystalline aggregate have identical c-axis orientations that are normal to an applied simple shear stress.
Reference Placidi, Greve, Seddik and FariaPlacidi and others (2010) suggest E max ≈ 10, based on experiments by Reference Pimienta, Duval and LipenkovPimienta and others (1987) on samples from the Vostok (East Antarctica) ice core with a strong single-maximum crystal orientation fabric. Other field and laboratory observations of simple shear strain-rate enhancement suggest potential E max values ranging from ∼4 to 12 (e.g. Reference Russell-Head and BuddRussell-Head and Budd, 1979; Reference DuvalDuval, 1981; Reference Azuma and HigashiAzuma and Higashi, 1984; Reference LileLile, 1984; Reference Dahl-Jensen and GundestrupDahl-Jensen and Gundestrup, 1987; Reference Pimienta, Duval and LipenkovPimienta and others, 1987; Reference Li, Jacka and BuddLi and others, 1996; Reference Morgan, Van Ommen, Elcheikh and LiMorgan and others, 1998; Reference Thorsteinsson, Waddington, Taylor, Alley and BlankenshipThorsteinsson and others, 1999). Here we specify a mid-range value of E max = 8 based on the compilation of Reference Treverrow, Budd, Jacka and WarnerTreverrow and others (2012). This value is consistent with selection of E s = 8, for the conceptually similar E s parameter in the B2013 flow relation.
Reference FariaFaria (2008) has demonstrated how the polycrystalline deformability, D (Eqn (20)), provides the anisotropic foundation of the scalar enhancement factor, E(D). The polycrystalline strain rate is
where the temperature-dependent flow parameter A(T) is as defined previously and the stress exponent n = 3. Due to the collinear relationship between components of ![]() and S, the CAFFE flow relation, Eqn (22), can readily be inverted to express
S
as a function of
and S, the CAFFE flow relation, Eqn (22), can readily be inverted to express
S
as a function of ![]() ,
,
Here ![]() is the effective shear strain rate (Reference NyeNye, 1957). Equation (23) requires the deformability, D, to be redefined as a function of
is the effective shear strain rate (Reference NyeNye, 1957). Equation (23) requires the deformability, D, to be redefined as a function of ![]() and
c
(Reference Placidi, Greve, Seddik and FariaPlacidi and others, 2010). Following Eqn (20),
and
c
(Reference Placidi, Greve, Seddik and FariaPlacidi and others, 2010). Following Eqn (20),

In the present study the instantaneous state of stress is calculated from strain-rate and fabric data via Eqns (23) and (24), which does not require the time (or strain)-dependent description of fabric evolution. Consequently, those aspects of CAFFE associated with the description of fabric evolution through the parameterization of recrystallization processes, including rigid body rotation, local grain rotation, polygonization and grain boundary migration, are not considered.
B2013 flow relation
The B2013 flow relation is based on an empirical parameterization of tertiary creep rates from laboratory ice-deformation experiments conducted in a range of combined stress configurations, incorporating various proportions of simple shear and compression components (Reference Budd, Warner, Jacka, Li and TreverrowBudd and others, 2013). In these experiments the compression axis was normal to the planes on which the forces generating the simple shear act. The flow relation is based on the observation that during tertiary creep the various statistically steady-state fabric patterns that develop correspond to the particular stress configuration (termed ‘compatible’ fabrics; Reference Budd, Warner, Jacka, Li and TreverrowBudd and others, 2013). This allows anisotropic flow to be parameterized directly from the relative proportions of the deviatoric stress components. Therefore, unlike the AGA, TNNI and CAFFE flow relations, specification of viscoplastic anisotropy in the B2013 does not require consideration of the magnitude of stresses resolved onto the basal planes of individual grains, i.e. fabric patterns are not required as an input to determine the flow.
The B2013 flow relation describes simple shear alone, compression alone or combined shear and compression stress configurations. The observation of similar levels of tertiary creep strain-rate enhancement for unconfined and confined compression (Reference Budd, Warner, Jacka, Li and TreverrowBudd and others, 2013) enables a flow relation where the relative proportions of the normal stress components in the directions parallel and transverse to the flow can be varied. This flow configuration is described as

where the parameter ζ describes the proportions of the normal components, ![]() and
and ![]() , where 0 ≤ ζ ≤ 1. We specify a coordinate system (corresponding to that chosen earlier for description of the DSS flow) where x is the horizontal flow direction within the non-rotating shear plane, z is the vertical and y the transverse direction. Values of ζ = 0 and ζ = 1 correspond to vertical compression with confinement in the y and x directions respectively, and ζ = 0.5 corresponds to unconfined compression where
, where 0 ≤ ζ ≤ 1. We specify a coordinate system (corresponding to that chosen earlier for description of the DSS flow) where x is the horizontal flow direction within the non-rotating shear plane, z is the vertical and y the transverse direction. Values of ζ = 0 and ζ = 1 correspond to vertical compression with confinement in the y and x directions respectively, and ζ = 0.5 corresponds to unconfined compression where ![]() .
.
In the B2013 flow relation the components of ![]() (Eqn (25)) are
(Eqn (25)) are
Anisotropy enters the flow relation through the weighted mean shear stress, T o (Reference Budd, Warner, Jacka, Li and TreverrowBudd and others, 2013):
In providing the nonlinearity of the flow relation T
o is analogous to the octahedral shear stress, τ
o, which is the root-mean-square average of the principal stress deviators (or τ
e in the Reference GlenGlen (1958) and CAFFE flow relations). E
s = 8 and E
c = 3 are experimentally determined shear and compression component enhancement factors. The asymmetry of T
o, through the different values for E
s and E
c in Eqn (27), parameterizes the experimentally observed anisotropy of tertiary creep strain-rate enhancement. Owing to the collinear relationship between the ![]() and
S
tensor components, Eqn (26) can be inverted to allow the components of
S
to be calculated from
and
S
tensor components, Eqn (26) can be inverted to allow the components of
S
to be calculated from ![]() . Unlike the AGA, CAFFE and TNNI flow relations, the particular form of the B2013 flow relation used here is not generalized to describe arbitrary flow configurations. It only applies to combinations of simple shear and compression represented by Eqn (25). As described in the following subsections, the large-scale flow regime at DSS is also described by Eqn (25), so the B2013 flow relation is suited to the examination of ice dynamics at this site.
. Unlike the AGA, CAFFE and TNNI flow relations, the particular form of the B2013 flow relation used here is not generalized to describe arbitrary flow configurations. It only applies to combinations of simple shear and compression represented by Eqn (25). As described in the following subsections, the large-scale flow regime at DSS is also described by Eqn (25), so the B2013 flow relation is suited to the examination of ice dynamics at this site.
The requirements for implementation of the B2013 flow relation are greatly simplified in comparison with the AGA, TNNI and CAFFE flow relations, since the anisotropy is determined from the stress configuration without reference to patterns of c-axis orientations. Implementation of B2013 in large-scale ice-sheet models, as outlined by Reference Budd, Warner, Jacka, Li and TreverrowBudd and others (2013), requires a generalization of the flow relation, from the particular situation of combined stresses studied in the laboratory experiments, to one applicable to arbitrary states of stress.
Calibration of the flow relations
All the flow relations considered here were calibrated using values of the temperature-dependent flow parameter, A(T) in Eqn (16), determined from the comprehensive Reference Budd and JackaBudd and Jacka (1989) compilation of secondary (minimum) creep octahedral shear strain rates determined for stresses from 0.025 to 0.40 MPa and temperatures from −50°C to −0.05°C. These A(T) values (Fig. 3) are substituted directly into the CAFFE and B2013 flow relations. For a statistically isotropic distribution of c-axis vectors, the CAFFE enhancement, E(D) = 1 (Eqn (21)). In this situation CAFFE reverts to the Reference GlenGlen (1958) relation and returns strain rates consistent with the Reference Budd and JackaBudd and Jacka (1989) compilation.
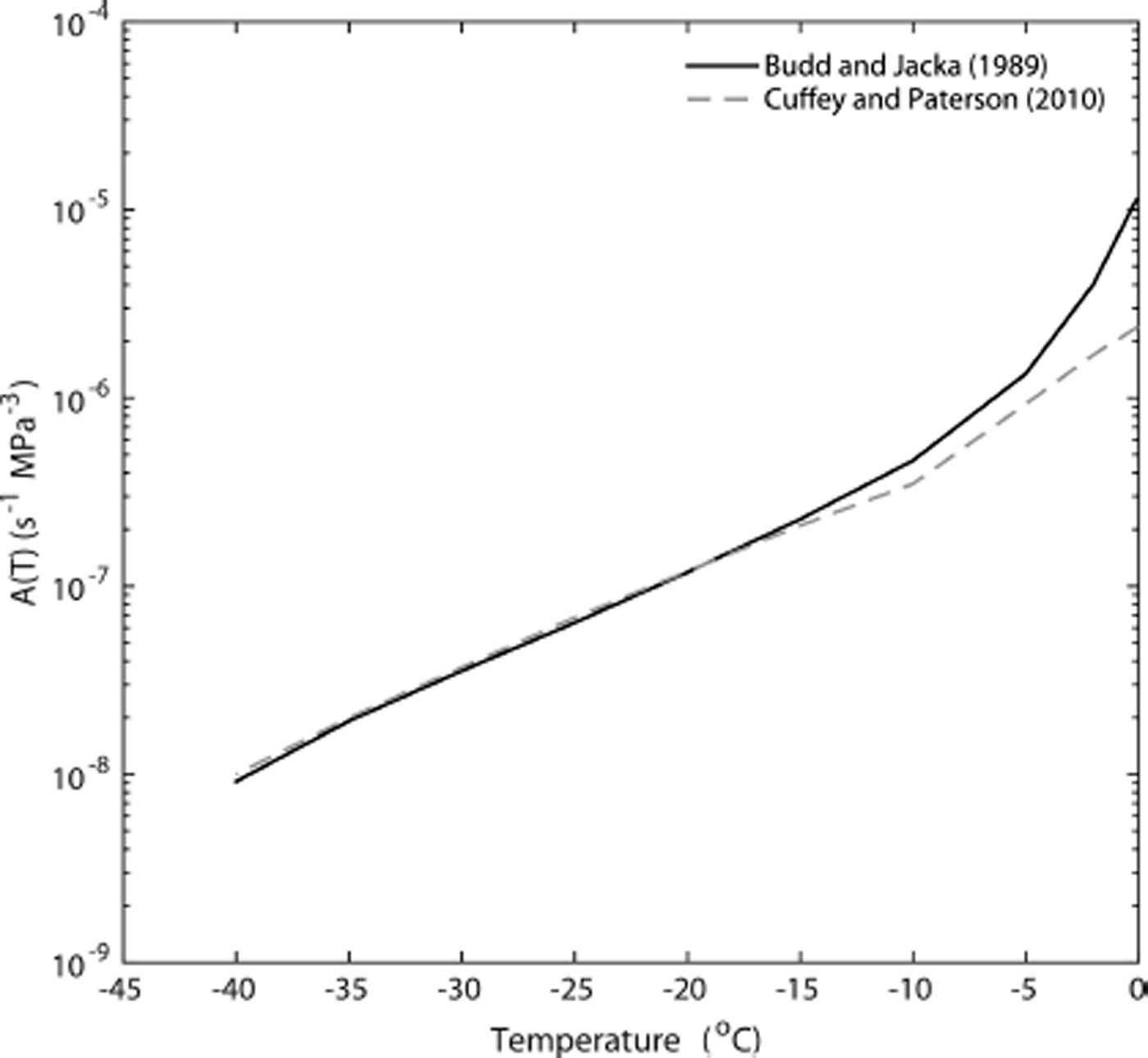
Fig. 3. Comparison of the Reference Budd and JackaBudd and Jacka (1989) and Reference Cuffey and PatersonCuffey and Paterson (2010) values of the temperature-dependent flow parameter, A(T) (Eqns (1) and (16)).
The A(T) values of Reference Cuffey and PatersonCuffey and Paterson (2010) are presented in Figure 3 for comparison with the values derived from the Reference Budd and JackaBudd and Jacka (1989) data. Over the temperature range in the DSS borehole of −21.8°C to −6.9°C the Reference Budd and JackaBudd and Jacka (1989) values are largely similar to those of Reference Cuffey and PatersonCuffey and Paterson (2010); however, above −15°C the Reference Budd and JackaBudd and Jacka (1989) derived values are more sensitive to increasing temperature, leading to higher values, particularly above −10°C.
In addition to A(T) values determined using the Reference Budd and JackaBudd and Jacka (1989) data, the TNNI flow relation, Eqn (18), is calibrated using the dimensionless parameter, B, to provide physically reasonable strain-rate (or stress) estimates (Eqns (15) and (16)). For strain rates calculated using a statistically isotropic distribution of N T ≈ 8.5 × 104 c-axes, the value of B required for strain rates to match the Reference Budd and JackaBudd and Jacka (1989) secondary (minimum) creep values varies according to the specified level of neighbour grain interaction, i.e. with the grain interaction parameters, C 0 and C n. Reference ThorsteinssonThorsteinsson (2001) provides an analytically derived value of B = 630 for homogeneous stress conditions with no neighbour grain interactions (e.g. C 0 = 1 and C n = 0), whilst for the case of full neighbour grain interaction, (C 0 = 1; C n = 1), we find B = 565.
In the derivation of the AGA flow relation, Reference Azuma and Goto-AzumaAzuma and Goto-Azuma (1996) used the temperature-dependent flow parameter, βS , specific to single-crystal deformation (Eqn (10)). For an isotropic distribution of c-axes this leads to strain rates three to four orders of magnitude higher than observed polycrystalline strain rates under similar conditions of temperature and stress (Reference TreverrowTreverrow, 2009). To correct this discrepancy we calibrate the AGA relation using a procedure similar to that for the TNNI relation. Using the same statistically isotropic distribution of N T ≈ 8.5 × 104 c-axes and the Reference Budd and JackaBudd and Jacka (1989) A(T), a scaling parameter is determined so that the isotropic strain rates match the Reference Budd and JackaBudd and Jacka (1989) secondary creep rates.
Calculation of stress profiles
Sensitivity of flow relations to fabric data array size
The parameterization of crystal orientation fabrics using an ODF may not adequately describe distributions where the number of c-axis orientations is <100. When implementing the flow relations to determine borehole stress profiles, we solve AGA, TNNI and CAFFE numerically, with discrete summations over the measured c-axis orientation data. This avoids any loss of fabric detail through conversion to a restrictive form of ODF.
Figure 4 illustrates how uncertainty in AGA, TNNI and CAFFE strain-rate predictions varies with the number of c-axis vectors in an isotropic fabric created by random selection from a simulated isotropic distribution of 8.5 × 104 axes. Normalized strain rates were calculated for simple shear on isotropic fabrics with N = 50 to 1.0 × 104
c-axes. For each N, 50 simulated fabrics were randomly selected from the original distribution and their normalized strain rates calculated. In each case the reference strain rates for normalization were calculated using the same isotropic distribution of 8.5 × 104 axes. These rates are equivalent to the analytically derived rates for an ideal isotropic distribution. For fabrics described by an array of c-axis vectors it is possible for the AGA and TNNI flow relations to predict ![]() components where there is no corresponding Sij
component. To incorporate the influence of this effect on the overall deformation, all normalized strain rates (Fig. 4) are calculated using octahedral shear strain rates.
components where there is no corresponding Sij
component. To incorporate the influence of this effect on the overall deformation, all normalized strain rates (Fig. 4) are calculated using octahedral shear strain rates.

Fig. 4. Variability in normalized octahedral shear strain rates as a function of N, the number of c-axes in simulated isotropic crystal orientation fabrics. Strain rates are for the (a) AGA, (b) TNNI and (c) CAFFE flow relations. For each value of N the mean and standard deviation of the octahedral shear strain rate were calculated for 50 simulated fabrics randomly selected from the same isotropic distribution of 8.5 × 104 axes. Strain rates calculated for each flow relation were normalized against rates determined using the reference isotropic fabric of 8.5 × 104 axes. Results for the TNNI flow relation were calculated with full neighbour grain interaction and CAFFE rates were calculated using E max = 8.
The uncertainty in strain rates predicted using the AGA, CAFFE and TNNI flow relations is highest for low-N fabrics due to the greater potential for individual grains, with a high degree of misorientation relative to the mean orientation, to influence the bulk strain rates. The values presented for isotropic fabrics (Fig. 4) represent an upper limit of c-axis orientation-based uncertainty in strain rates for each N. As fabrics become increasingly anisotropic the mean misorientation of c-axes decreases, reducing the potential for any individual grains to strongly influence the bulk strain rates. In this study we use fabric data measurements that predate modern automated ice crystal fabric analysers, so individual fabrics are restricted to N ≈ 100 orientations due to the arduous nature of conducting multiple Rigsby stage analyses (Fig. 2c). For anisotropic fabrics, measurement of N ≈ 80–100 c-axes is adequate to describe the distribution (e.g. Reference Durand, Gagliardini, Thorsteinsson, Svensson, Kipfstuhl and Dahl-JensenDurand and others, 2006; Reference Gow and MeeseGow and Meese, 2007); however, this value increases as fabrics become increasingly isotropic.
To minimize uncertainty in the flow relation stress estimates based on fabrics with N < 100, composite fabrics have been created by combining five sequential fabrics, resulting in N ≈ 500. This smooths the fabric data over an interval of ∼25–40 m (bold lines in Fig. 2c). The depth assigned to each of the 185 composites is the moving mean of the five contributing fabric depths. With this technique the number of individual fabrics contributing to the composites is lower for the uppermost and lowermost two cases, which are derived from three and four members respectively.
Flow configuration at DSS
From surface and borehole strain-rate observations (Reference Morgan, Van Ommen, Elcheikh and LiMorgan and others, 1998) the flow configuration at the DSS site is assumed to be horizontal simple shear parallel to the surface flow direction, combined with extension both parallel and transverse to the flow direction. This flow configuration corresponds to that specified for the B2013 flow relation in Eqn (25). The ζ parameter describing the relative proportions of the normal flow components can be determined from the ratio of the GPS-determined surface strain-rate components, i.e. ![]() (Table 1), leading to
(Table 1), leading to ![]() and
and

so that vertical profiles of ![]() and
and ![]() can be obtained from the
can be obtained from the ![]() profile. The agreement between the surface value of the vertical strain-rate profile,
profile. The agreement between the surface value of the vertical strain-rate profile, ![]() (Eqns (3) and (4)) and the GPS-determined
(Eqns (3) and (4)) and the GPS-determined ![]() (Reference Morgan, Van Ommen, Elcheikh and LiMorgan and others, 1998) provides validation of the borehole inclination derived
(Reference Morgan, Van Ommen, Elcheikh and LiMorgan and others, 1998) provides validation of the borehole inclination derived ![]() profile.
profile.
Procedures for estimating stress profiles
The procedures used to estimate Sxz
and Szz
profiles using the available strain-rate, temperature and crystal orientation data vary for each flow relation. We calculate the vertical deviator, Szz
, since ![]() links more directly to the calculated
links more directly to the calculated ![]() profile (Eqn (3)). In all cases a stress configuration of the form
profile (Eqn (3)). In all cases a stress configuration of the form

is assumed where ![]() is used. The borehole strain-rate
is used. The borehole strain-rate ![]() and temperature data (Fig. 2) are available at higher spatial resolution than the fabric data, so values corresponding to the composite fabric depths were determined by interpolation.
and temperature data (Fig. 2) are available at higher spatial resolution than the fabric data, so values corresponding to the composite fabric depths were determined by interpolation.
Owing to the collinear relationship between ![]() and
S
components in the B2013 flow relation, at each depth interval
and
S
components in the B2013 flow relation, at each depth interval ![]() . From the depth profile of
. From the depth profile of ![]() , substitution of
, substitution of ![]() into Eqns (26) and (27) gives
into Eqns (26) and (27) gives

from which Szz is easily obtained.
For the CAFFE flow relation Sxz and Szz are calculated using the composite fabric data appropriate to each depth (Eqns (21) and (23)).
For the AGA and TNNI flow relations a tensor relationship exists between ![]() and
S
, necessitating indirect calculation of stress profiles via a more complex two-step process. Firstly, temperature-independent
and
S
, necessitating indirect calculation of stress profiles via a more complex two-step process. Firstly, temperature-independent ![]() values were calculated for each fabric using
S
(Eqn (29)), where the proportions of Sxz
and Szz
were varied iteratively for values of a shear stress parameter (Reference Warner, Jacka, Li, Budd, Hutter, Wang and BeerWarner and others, 1999),
values were calculated for each fabric using
S
(Eqn (29)), where the proportions of Sxz
and Szz
were varied iteratively for values of a shear stress parameter (Reference Warner, Jacka, Li, Budd, Hutter, Wang and BeerWarner and others, 1999),
where 0 ≤ r
s ≤ 1. The shear parameter r
s = 0 when Sxz
= 0, and r
s = 1 when Szz
= 0. When Sxz
= Szz
(equal deviators) r
s = 0.5. For each composite fabric the rs
value that produces the strain-rate ratio, ![]() , which matches the borehole-derived value for that depth was determined. In this step, only the relative proportions of Sxz
and Szz
are required since
, which matches the borehole-derived value for that depth was determined. In this step, only the relative proportions of Sxz
and Szz
are required since ![]() is a function of the fabric and r
s, i.e. their magnitudes and the temperature dependence are unimportant, only their relative proportion matters. Secondly,
is a function of the fabric and r
s, i.e. their magnitudes and the temperature dependence are unimportant, only their relative proportion matters. Secondly, ![]() was recalculated for each composite fabric using the appropriate A(T) value (Eqn (16)), for the corresponding depth. For each fabric the magnitudes of Sxz
and Szz
were varied iteratively, according to the proportions described by the corresponding r
s value, until the correct borehole
was recalculated for each composite fabric using the appropriate A(T) value (Eqn (16)), for the corresponding depth. For each fabric the magnitudes of Sxz
and Szz
were varied iteratively, according to the proportions described by the corresponding r
s value, until the correct borehole ![]() and
and ![]() values were reproduced.
values were reproduced.
Results
The calculated vertical profiles of Sxz , Szz and τ o for the AGA, TNNI, CAFFE and B2013 flow relations are presented in Figure 5a, b and c respectively. The octahedral shear stress, τ o, provides a comparison of generalized stress magnitude for each flow relation. As a reference, Sxz , Szz and τ o profiles have also been calculated for the Reference GlenGlen (1958) flow relation, Eqn (1), using the borehole deformation and temperature data. The Glen Sxz profile is given by

Fig. 5. Stress profiles as a function of ice equivalent depth at the DSS borehole site (Law Dome), calculated using the AGA, CAFFE, TNNI and B2013 flow relations. (a) Shear stress, Sxz ; (b) compression deviatoric stress, Szz ; and (c) octahedral shear stress, τ o. Note the different horizontal scales. Estimates of the one standard deviation (σ) uncertainty intervals for Sxz , Szz and τ o are based on the variability in the borehole strain rate (Fig. 2b) and c-axis orientation fabric (Fig. 2c) datasets.

where ![]() and ζ are as defined previously. The collinear relationship between
and ζ are as defined previously. The collinear relationship between ![]() and
S
in Eqn (1) allows the vertical deviatoric stress component to be determined from
and
S
in Eqn (1) allows the vertical deviatoric stress component to be determined from ![]() .
.
In addition to the Sxz
, Szz
and τ
o profiles (Fig. 5), differences between the flow relations are illustrated through the calculation of the profiles for strain-rate-based flow enhancement ratios, Exz
and Ezz
(Fig. 6). Exz
and Ezz
were determined from the ratio of the DSS borehole strain-rate components, ![]() and
and ![]() , to the corresponding strain rates calculated using the Reference GlenGlen (1958) flow relation (Eqn (1)), and the Sxz
and Szz
profiles determined for each anisotropic flow relation (Fig. 5a and b). Here the Reference GlenGlen (1958) flow relation is used without any modification to account for flow enhancement effects. This provides a quantitative basis for comparison of the anisotropic flow relations with one another, and an assessment of the enhancement factors used with the isotropic Reference GlenGlen (1958) flow relation in ice-sheet models (e.g. Reference CalovCalov and others, 2010) that are typically independent of the flow configuration and may vary from E ≈ 3 to E ≈ 12, depending on the chosen reference value.
, to the corresponding strain rates calculated using the Reference GlenGlen (1958) flow relation (Eqn (1)), and the Sxz
and Szz
profiles determined for each anisotropic flow relation (Fig. 5a and b). Here the Reference GlenGlen (1958) flow relation is used without any modification to account for flow enhancement effects. This provides a quantitative basis for comparison of the anisotropic flow relations with one another, and an assessment of the enhancement factors used with the isotropic Reference GlenGlen (1958) flow relation in ice-sheet models (e.g. Reference CalovCalov and others, 2010) that are typically independent of the flow configuration and may vary from E ≈ 3 to E ≈ 12, depending on the chosen reference value.

Fig. 6. Vertical profiles of the simple-shear and vertical-compression strain-rate enhancement factors for the each of the anisotropic flow relations. The enhancements, Eij
, are the ratio of the borehole strain rates to the corresponding values calculated with the Reference GlenGlen (1958) flow relation using borehole temperature data and the stress estimates from each of the anisotropic flow relations (Fig. 5a and b). For the collinear CAFFE and B2013 flow relations (a), the same enhancement ratio applies for both the shear (Exz
) and compression (Ezz
) components. In the (b) AGA and (c) TNNI flow relations, the ![]() and
S
components are related by a tensor-viscosity term, resulting in separate Exz
and Ezz
profiles.
and
S
components are related by a tensor-viscosity term, resulting in separate Exz
and Ezz
profiles.
The small-scale fluctuations in the Sxz
, Szz
and τ
o profiles over intervals of ∼10–20 m (Fig. 5) are a direct consequence of measurement-related variability of the fabric and strain-rate data and are not expected to reflect the existence of corresponding noise in the in situ stress profiles. The magnitude of the small-scale fluctuations varies with the flow relations and is related to the manner in which fabric and strain-rate (or stress) data are incorporated into the flow predictions. The AGA and TNNI flow relations are most susceptible to this induced variability as the bulk deformation is based on the homogenization of individual grain responses. The enhancement factor profiles (Fig. 6) indicate how the small-scale variability in the AGA and TNNI stress predictions – in particular that due to fabric – is amplified for the minor flow component, i.e. when ![]() or vice versa. This is clearly demonstrated in the Exz
profiles above ∼300 m where
or vice versa. This is clearly demonstrated in the Exz
profiles above ∼300 m where ![]() and below ∼800 m where
and below ∼800 m where ![]() . For the CAFFE flow relation the potential for individual grain c-axis orientations, or groups of grains, to introduce noise into the stress profile is reduced since homogenization occurs through the scalar anisotropic enhancement factor. As c-axis orientation data are not a required input for the B2013 flow relation, the predicted Sxz
and Szz
, profiles are only influenced by noise in
. For the CAFFE flow relation the potential for individual grain c-axis orientations, or groups of grains, to introduce noise into the stress profile is reduced since homogenization occurs through the scalar anisotropic enhancement factor. As c-axis orientation data are not a required input for the B2013 flow relation, the predicted Sxz
and Szz
, profiles are only influenced by noise in ![]() and
and ![]() , which are derived from the borehole inclination data.
, which are derived from the borehole inclination data.
Discussion
The shear stress profiles are similar for all anisotropic flow relations (Fig. 5a). This result is not surprising since all the flow relations, despite their differing formulations, are optimized to predict enhanced shear deformation rates where the flow is shear-dominated. The CAFFE, AGA and TNNI flow relations derive their representation of polycrystalline anisotropy from the distribution of crystal c-axis orientations and their relationship to the applied stresses. Consequently predictions of enhanced shear deformation are to be expected at the DSS site where the flow is shear-dominated (at depths greater than ∼600 m) and the crystal orientation fabrics tend towards a strong vertical single maximum which is compatible with the flow regime. For all flow relations the predicted anisotropic flow enhancement reduces the magnitude of Sxz
required to drive the observed ![]() in comparison with the isotropic Reference GlenGlen (1958) flow relation. The magnitudes of the LGM shear strain rates at ∼1120 m are nearly double the rates associated with the broad maximum in shear rates at ∼1000 m (Fig. 2c). However, due to the effects of higher ice temperatures at depth on increasing the ice fluidity, the Sxz
values in these two zones are similar for all flow relations.
in comparison with the isotropic Reference GlenGlen (1958) flow relation. The magnitudes of the LGM shear strain rates at ∼1120 m are nearly double the rates associated with the broad maximum in shear rates at ∼1000 m (Fig. 2c). However, due to the effects of higher ice temperatures at depth on increasing the ice fluidity, the Sxz
values in these two zones are similar for all flow relations.
In combined stress configurations it is important that the magnitudes of all predicted stress components are considered simultaneously. While the Sxz profiles are similar for each flow relation, significant differences exist in their Szz profiles due to their varying representations of polycrystalline anisotropy, particularly in complex stress configurations.
The Szz
estimates for the B2013 flow relation are consistently lower than those for the other relations considered. This is a consequence of the underlying phenomenological basis of the flow relation using experimental tertiary creep rates. The effective enhancement (Fig. 6a) varies from a minimum of E ≈ 3 near the surface where ![]() , to E ≈ 8 below ∼800 m where
, to E ≈ 8 below ∼800 m where ![]() .
.
In the compression-dominated zone from the surface down to ∼550 m, where ![]() (Figs 2b and 5b), the depth-averaged compression enhancement for the B2013 flow relation is Ezz
= 3.38. This value is similar to observations of tertiary creep from compression alone or compression-dominated flow regimes. Over this same zone, the corresponding crystal c-axis fabrics are weakly clustered, displaying a broad single maximum. For the AGA, TNNI and CAFFE relations – where the description of anisotropy is at least partly based on the magnitude of applied stresses resolved onto the basal planes of individual grains – the resulting Ezz
values are lower. For both CAFFE and AGA, Ezz
= 1.44 and Ezz
= 1.27 for TNNI. These values are significantly lower than expectations from laboratory experiments in tertiary creep where
(Figs 2b and 5b), the depth-averaged compression enhancement for the B2013 flow relation is Ezz
= 3.38. This value is similar to observations of tertiary creep from compression alone or compression-dominated flow regimes. Over this same zone, the corresponding crystal c-axis fabrics are weakly clustered, displaying a broad single maximum. For the AGA, TNNI and CAFFE relations – where the description of anisotropy is at least partly based on the magnitude of applied stresses resolved onto the basal planes of individual grains – the resulting Ezz
values are lower. For both CAFFE and AGA, Ezz
= 1.44 and Ezz
= 1.27 for TNNI. These values are significantly lower than expectations from laboratory experiments in tertiary creep where ![]() . Data from both combined- and single-stress component experiments clearly demonstrate that during tertiary creep, all strain-rate components are enhanced relative to the expectations from the Reference GlenGlen (1958) flow relation (Reference Li, Jacka and BuddLi and others, 1996; Reference Treverrow, Budd, Jacka and WarnerTreverrow and others, 2012; Reference Budd, Warner, Jacka, Li and TreverrowBudd and others, 2013).
. Data from both combined- and single-stress component experiments clearly demonstrate that during tertiary creep, all strain-rate components are enhanced relative to the expectations from the Reference GlenGlen (1958) flow relation (Reference Li, Jacka and BuddLi and others, 1996; Reference Treverrow, Budd, Jacka and WarnerTreverrow and others, 2012; Reference Budd, Warner, Jacka, Li and TreverrowBudd and others, 2013).
Between ∼550 m and ∼1000 m, where the flow is increasingly shear-dominated and fabrics tend towards a single maximum, the CAFFE Szz
rapidly decreases towards values approaching those of B2013. This reduction is driven by an increase in the macroscopic enhancement from E ≈ 2 to E ≈ 7 and the collinearity of the ![]() and
S
components.
and
S
components.
In contrast to the collinear CAFFE and B2013 flow relations, the full tensor viscosities prescribed by the AGA and TNNI relations allow the component enhancements to differ. Consequently, the high levels of shear enhancement that evolve below ∼550 m do not contribute to a reduction in Szz . This leads to Szz predictions that are considerably higher than the B2013 and CAFFE values, particularly at depths below the upper compression-dominated region (≤550 m) at the DSS site.
Within the shear-dominated zone from ∼550 m to 1000 m the AGA and TNNI Szz predictions even exceed the estimates for the isotropic Reference GlenGlen (1958) flow relation, corresponding to component enhancements of Ezz < 1 (Fig. 6b and c). Because the high-strain deformation associated with tertiary creep processes prevails at Law Dome (Reference Russell-Head and BuddRussell-Head and Budd, 1979; Reference Budd and JackaBudd and Jacka, 1989; Reference EtheridgeEtheridge, 1989; Reference Morgan, Van Ommen, Elcheikh and LiMorgan and others, 1998), the AGA and TNNI predictions of Ezz < 1 are indicative of physically unrealistic descriptions of anisotropic ice rheology in complex flow regimes. In particular, their predictions of a resistance to vertical compression – that exceeds the expectations for the isotropic Reference GlenGlen (1958) flow relation – is contrary to observations of tertiary creep in combined simple shear and confined vertical compression experiments (Reference Li, Jacka and BuddLi and others, 1996; Reference Budd, Warner, Jacka, Li and TreverrowBudd and others, 2013). These effects are investigated further in the following subsection.
Comparison with observations from laboratory ice-deformation experiments
While prediction of Sxz and Szz profiles using ice-core and borehole data allows differentiation of the flow relations based on their description of anisotropic rheology, such a comparison does not provide an assessment of whether or not the relative proportions of the stress tensor components are physically realistic. In the following we use data from laboratory ice deformation experiments to support our analysis of the AGA, TNNI, CAFFE and B2013 flow relations.
In experiments on laboratory-made ice conducted in combined simple shear and confined vertical compression stress configurations, with different proportions of Sxz and Szz , Reference Li, Jacka and BuddLi and others (1996) and Reference Budd, Warner, Jacka, Li and TreverrowBudd and others (2013) demonstrated that during tertiary creep all strain-rate components were enhanced relative to the expectations from the Reference GlenGlen (1958) flow relation. In particular the compression rates were enhanced, even as the shear stress proportion increased and became dominant. Furthermore, this enhancement occurs despite the development of compatible fabric patterns that might be considered to contain a high proportion of hard-glide c-axis orientations with respect to the compressive deviatoric stress component. The general similarity of the DSS-site flow configuration and that of the experiments of Reference Li, Jacka and BuddLi and others (1996) and Reference Budd, Warner, Jacka, Li and TreverrowBudd and others (2013) allows for a comparison of DSS- and experimentally based flow relation predictions.
Strain-rate and c-axis orientation data from two experiments in the series of Reference Budd, Warner, Jacka, Li and TreverrowBudd and others (2013), and another conducted using the same apparatus and experimental techniques as Reference Budd, Warner, Jacka, Li and TreverrowBudd and others (2013), were used to calculate the ratio of the simple shear and confined compression deviatoric stresses, Sxz
/Szz
. In Table 2 these values are compared to the applied experimental stresses. We examine cases where the applied ratios of deviatoric stresses were Sxz
/Szz
= 0.5, 1.0 and 2.0. The corresponding strain-rate ratios for these experiments were ![]() , 1.05 and 1.59, respectively (Table 2). These values are generally consistent with a collinear relationship between the components of
, 1.05 and 1.59, respectively (Table 2). These values are generally consistent with a collinear relationship between the components of ![]() and
S
: the ≤20% difference between the stress and strain-rate component ratios is within the 95% confidence interval for the variability between replicate experiments (Reference Treverrow, Budd, Jacka and WarnerTreverrow and others, 2012).
and
S
: the ≤20% difference between the stress and strain-rate component ratios is within the 95% confidence interval for the variability between replicate experiments (Reference Treverrow, Budd, Jacka and WarnerTreverrow and others, 2012).
Table 2. The ratio of simple shear and vertical compression deviatoric stress tensor components calculated using experimental tertiary creep rate and c-axis orientation fabric data. The initially isotropic polycrystalline ice samples were deformed in combined stress configurations incorporating various proportions of simple shear and confined vertical compression. All experiments were conducted at −2°C. Experimental data for (b) and (c) are from Reference Budd, Warner, Jacka, Li and TreverrowBudd and others (2013) (table 1, experiments 22 and 24, respectively). The data for (a) were obtained using the same apparatus and experimental techniques as Reference Budd, Warner, Jacka, Li and TreverrowBudd and others (2013). (a) Compression-dominated with Sxz /Szz = 0.50, Sxz = 0.219 MPa and τ o = 0.40 MPa. (b) Equal shear and compression deviators, Sxz /Szz = 1.0, Sxz = 0.49 MPa and τ o = 0.57 MPa. (c) Shear-dominated with with Sxz /Szz = 2.0, Sxz = 0.49 MPa and τ o = 0.45 MPa. The experimental stress configuration is defined by a Cartesian coordinate system where the x-axis is the shear direction and the z-axis is normal to the plane of the page. The crystal orientation data are presented in lower-hemisphere Schmidt plots aligned with the xy-plane

Due to the collinearity of the B2013 and CAFFE flow relations the stress ratios calculated for the experiments are precisely the strain-rate component ratios. Thus, for the experiments where Sxz
/Szz
= 1.0 and 2.0 the B2013 and CAFFE relations return Sxz
/Szz
= 1.05 and 1.59 (cf. the corresponding strain-rate ratios of ![]() and 1.59, respectively, in Table 2). In contrast the AGA and TNNI relations predict significantly lower Sxz
/Szz
ratios that are only 40–49% of the B2013/CAFFE values. These low AGA and TNNI Sxz
/Szz
values in flow configurations where Sxz
≥ Szz
are consistent with the presented DSS borehole analysis. Figure 5 demonstrates how the four anisotropic flow relations predict similar Sxz
values using the DSS borehole and ice-core data: it is the marked variability in their Szz
predictions that drives differences in the Sxz
/Szz
ratio. Therefore, the Sxz
/Szz
values predicted by the AGA and TNNI relations are inconsistent with tertiary creep observations from combined simple shear and confined vertical compression experiments where
and 1.59, respectively, in Table 2). In contrast the AGA and TNNI relations predict significantly lower Sxz
/Szz
ratios that are only 40–49% of the B2013/CAFFE values. These low AGA and TNNI Sxz
/Szz
values in flow configurations where Sxz
≥ Szz
are consistent with the presented DSS borehole analysis. Figure 5 demonstrates how the four anisotropic flow relations predict similar Sxz
values using the DSS borehole and ice-core data: it is the marked variability in their Szz
predictions that drives differences in the Sxz
/Szz
ratio. Therefore, the Sxz
/Szz
values predicted by the AGA and TNNI relations are inconsistent with tertiary creep observations from combined simple shear and confined vertical compression experiments where ![]() .
.
For the compression-dominated experiment, where Sxz /Szz = 0.5 (Table 2), the predictions of the AGA and TNNI flow relations correspond more closely to the experimental observations and the B2013 and CAFFE relations. This improved performance is related to the generally decreasing strength of the c-axis fabrics in these flow configurations. The weakly clustered fabric for the experiment where Sxz /Szz = 0.5 exhibits a low level of compatibility with both the simple shear and confined compression components. For the AGA and TNNI flow relations this results in moderate enhancement of both strain-rate components and predicted stress ratios that agrees well with the expected value of Sxz /Szz = 0.5.
As the experiments become increasingly shear-dominated, i.e. where Sxz ≥ Szz , the fabrics evolve towards distributions containing a higher proportion of near-vertical c-axes. The very low vertical compressive stress components resolved on the basal planes of grains with near-vertical c-axes drive the high Szz values that are necessary to reproduce the experimental observations.
This assessment of the flow relations using experimental data is consistent with the analysis based on DSS borehole and ice-core data. For each experiment in Table 2, we identify the DSS borehole depths where the derived strain-rate ratios, ![]() , are equivalent to the experimental values. As was found for the stress ratios calculated using experimental data, the DSS borehole Sxz
/Szz
values, at the specific depths corresponding to the experiment-based simulations, indicate how the AGA and TNNI flow relations consistently overestimate Szz
, particularly where
, are equivalent to the experimental values. As was found for the stress ratios calculated using experimental data, the DSS borehole Sxz
/Szz
values, at the specific depths corresponding to the experiment-based simulations, indicate how the AGA and TNNI flow relations consistently overestimate Szz
, particularly where ![]() .
.
While data from the combined stress experiments necessary to investigate the collinearity of flow relations are currently sparse (e.g. Reference Li, Jacka and BuddLi and others, 1996; Reference Budd, Warner, Jacka, Li and TreverrowBudd and others, 2013), we are not aware of any data that support the low Sxz /Szz values predicted by the AGA and TNNI flow relations in complex stress configurations where the flow is shear-dominated. Further laboratory studies to investigate these combined-stress configuration effects are ongoing. More generally, this study demonstrates the difficulties associated with the development of flow relations based on a grain-scale description of deformation and recovery processes: unless all processes important to the flow are adequately described, the prescribed rheology will be incomplete and potentially unrealistic.
General comments on anisotropic flow relation formulation and polycrystalline ice deformation
Numerous field and laboratory observations indicate how polycrystalline ice rheology is influenced by a range of factors including the large-scale flow pattern, stress, temperature and microstructural evolution (e.g. Reference Russell-Head and BuddRussell-Head and Budd, 1979; Reference Dahl-Jensen and GundestrupDahl-Jensen and Gundestrup, 1987; Reference Wang and WarnerWang and Warner, 1999; Reference Wang, Warner and BuddWang and others, 2002; Reference DurandDurand and others, 2007). However, the conspicuous nature of fabric evolution, and its association with anisotropic deformation has led to the development of flow relations such as AGA, TNNI and CAFFE where the pattern of c-axis orientations and their relationship to the stress configuration is the principal control on the anisotropic flow.
The analyses presented here illustrate that anisotropic effects are more complex than may be explained by flow relations based (largely) on the magnitude of stresses resolved onto the basal planes of individual grains. More fundamentally, looking beyond anisotropy, it is demonstrated that fabric is not the dominant process in controlling the magnitude of polycrystalline strain rates.
The importance of micro-dynamic processes occurring at grain boundaries can be understood through a comparison of single and polycrystalline ice deformation rates. Under conditions of similar temperature and stress the secondary (minimum) creep rates for polycrystalline ice with randomly oriented grains are about three orders of magnitude less than those for single crystals oriented for easy glide on basal planes (Reference Duval, Ashby and AndermanDuval and others, 1983; Reference TreverrowTreverrow, 2009). During tertiary creep the microstructure (fabric and grain size) evolves in response to the stress configuration and magnitude (e.g. Reference LileLile, 1978), leading to higher strain rates and the development of polycrystalline anisotropy. Despite these microstructural changes, tertiary creep rates (e.g. Reference Gao and JackaGao and Jacka, 1987; Reference Budd and JackaBudd and Jacka, 1989; Reference Treverrow, Budd, Jacka and WarnerTreverrow and others, 2012; Reference Budd, Warner, Jacka, Li and TreverrowBudd and others, 2013) remain about two orders of magnitude below the corresponding easy-glide single crystal rates. This disparity illustrates the dissipative effect of grain-boundary processes and their proportionally greater influence on the magnitude of polycrystalline strain rates compared with the development of anisotropy. Discussion of the relative contribution of the various micro-deformation, recovery and recrystallization processes important to polycrystalline ice rheology is beyond the scope of this work (see, e.g., Reference Piazolo, Wilson, Luzin, Brouzet and PeternellPiazolo and others, 2013; Reference Faria, Weikusat and AzumaFaria and others, 2014; Reference MontagnatMontagnat and others, 2014b; Reference Wilson, Peternell, Piazolo and LuzinWilson and others, 2014). However, it is clear that if grain boundary processes were not important, polycrystalline deformation rates would more closely approach the corresponding single crystal values in tertiary creep situations, where strongly oriented fabrics result in a high proportion of c-axes in easy-glide orientations, relative to the applied stress.
The above considerations are important to the assessment of the AGA and TNNI flow relations, both of which incorporate grain orientation and nearest-neighbour grain interactions into their rheological description. The necessity for arbitrary scaling, using an additional term that is separate from the temperature-dependent flow parameter, to ensure that predictions for a random c-axis distribution match reference values for secondary (isotropic minimum) creep rates is indicative of an incomplete description of polycrystalline behaviour (e.g. the scaling parameter B in Eqn (15) for TNNI, and the requirement to discard βs in Eqn (9) for the AGA relation). This highlights the difficulty of developing a physically based flow relation which incorporates the description of micro-dynamic processes. Achieving a realistic rheology requires the identification of all relevant processes, and their incorporation via either explicit modelling or through parameterization of their effects.
While the CAFFE flow relation is similar to AGA and TNNI in that intracrystalline slip on basal planes is assumed to be the dominant deformation mechanism, and the source of polycrystalline anisotropy, it differs from these relations as orientation relationships between the fabric and applied stresses define a scalar anisotropic enhancement factor, rather than determining the strain rate of an individual grain. Owing to the experimentally observed complementary enhancement effect between simple shear and compression components during tertiary creep (Reference Budd, Warner, Jacka, Li and TreverrowBudd and others, 2013) the B2013 and CAFFE flow relations, where the ![]() and Sij
components are related by a scalar anisotropic function, are better suited to the description of polar ice dynamics.
and Sij
components are related by a scalar anisotropic function, are better suited to the description of polar ice dynamics.
Future flow relation developments
A primary consideration in the development of flow relations for ice-sheet modelling is to minimize the computational cost while improving the representation of anisotropic rheology. The CAFFE and B2013 flow relations are based on parameterizations of key rheological variables with resultant low computational overhead and, particularly for B2013, have relatively straightforward requirements for implementation within ice-sheet models. Of the flow relations investigated here, the CAFFE and B2013 flow relations provide the most physically realistic predictions of deviatoric stresses at the DSS site, despite their relative simplicity.
While the CAFFE flow relation has been implemented in the 3-D FEM full-Stokes ice-sheet model Elmer/Ice (Reference GagliardiniGagliardini and others, 2013), to investigate regional ice-sheet dynamics around deep ice-core drilling sites (Reference Seddik, Greve, Placidi, Hamann and GagliardiniSeddik and others, 2008) the computational cost and complexity of a scheme describing the spatial and temporal evolution of crystal orientation fabrics so far prohibit its application in long-term continental-scale simulations.
The anisotropy of the B2013 flow relation (Eqn (27)) is determined from the relative proportions of the deviatoric stress (or strain-rate) components, eliminating the requirement to simulate fabric evolution in forward modelling. The B2013 flow relation is based on data from laboratory deformation experiments conducted in stress configurations incorporating specific combinations of simple shear and vertical compression. While these stress configurations are relevant to describing the flow regime at DSS, a generalized form of the B2013 flow relation, as described by Reference Budd, Warner, Jacka, Li and TreverrowBudd and others (2013), is required for large-scale dynamic simulations where a wider range of stress configurations is encountered.
The physically motivated descriptions of intra- and intercrystalline deformation and recovery processes in the AGA and TNNI flow relations lead to complex rheologies with tensor descriptions of viscosity. Whilst some full-Stokes models provide the necessary framework to support anisotropic tensor viscosities, the additional complexity of the AGA and TNNI flow relations, including the requirement to simulate fabric evolution, precludes their application in continental-scale ice-sheet models. Application of the TNNI relation is further restricted by the explicit inclusion of nearest-neighbour grain interactions. Rather than being directly applied in ice-sheet models the future benefit of such physically motivated flow relations lies in their value as tools to improve understanding of intra- and intercrystalline deformation and recrystallization processes (e.g. Reference LlorensLlorens and others, 2014; Reference MontagnatMontagnat and others, 2014b). The identification of commonalities in the microstructure and deformation processes observed in laboratory and ice-core samples, in conjunction with microstructure modelling, will support the development of phenomenological flow relations for ice-sheet modelling, and their extrapolation to a broader range of temperature and stress conditions than can be readily achieved in laboratory studies.
The continued development of anisotropic flow relations for ice-sheet modelling relies on the availability of laboratory, field and remotely sensed observations of ice dynamics. In general, reliable experimental data for flow relation development are sparse, with tertiary creep observations even more limited. Additional statistically robust strain-rate data and microstructural observations are required to extend the range of stress configurations, magnitudes and temperatures over which an improved anisotropic flow relation can be reliably specified. For example, a creep power law stress exponent of n = 3 in Eqn (1) is well established for secondary (isotropic minimum) strain rates. Analysis by Reference Treverrow, Budd, Jacka and WarnerTreverrow and others (2012) of the limited available tertiary creep data from shear alone and compression alone experiments suggests a stress exponent of n = 3.5 may be appropriate for describing tertiary creep, at least for some stress configurations (and possibly stress magnitudes; e.g. Reference PettitPettit and others (2011) discuss the transition to a flow regime with n = 1 at low stresses). In the context of a Glen-type flow relation, a stress exponent of n = 3.5 may be paramaterized by a stress-dependent enhancement factor, ![]() , where
, where
Further experimental data are required to validate this effect over a wider range of stress configurations and temperatures. Prescription of a stress-dependent enhancement term to accommodate a flow relation where n = 3.5 would be straightforward for the CAFFE and B2013 flow relations, and others with an experimentally derived scalar enhancement term (e.g. Reference Pettit, Thorsteinsson, Jacobson and WaddingtonPettit and others, 2007).
Summary and Conclusions
Deep ice cores for which there are corresponding borehole temperature and strain-rate data are an extraordinarily valuable resource for evaluating polycrystalline ice flow relations. In this study the anisotropic CAFFE (Reference Placidi, Greve, Seddik and FariaPlacidi and others, 2010), AGA (Reference Azuma and Goto-AzumaAzuma and Goto-Azuma, 1996), TNNI (Reference ThorsteinssonThorsteinsson, 2002) and B2013 (Reference Budd, Warner, Jacka, Li and TreverrowBudd and others, 2013) flow relations were compared using data from the DSS ice core and borehole at Law Dome to calculate depth profiles of the stresses required to drive the observed ice flow.
The B2013 flow relation is an empirical parameterization of experimental tertiary creep rates where the magnitude of anisotropic effects is controlled by the relative proportion of strain rate (or stress components). This eliminates the requirement for a numerical fabric evolution scheme and simplifies the requirements for its implementation in an ice-sheet model.
The anisotropy of the AGA, TNNI and CAFFE flow relations is predominantly derived from the way applied stresses are resolved onto the basal planes of individual grains and the homogenization method used to determine the macroscopic strain rates. Despite differences in their rheological descriptions, the conceptual similarity of these relations results in the maximum levels of flow enhancement being predicted where the resolved stresses on the basal planes are highest (e.g. where vertical single-maximum fabrics coexist with a flow regime dominated by approximately bed-parallel shear). Such conditions occur at depths from ∼550 m to ∼1100 m at the DSS site, and the shear stress profiles, Sxz , for each of the anisotropic flow relations are similar. In each case the predicted Sxz values were lower than those for the isotropic Glen flow relation.
In complex flow regimes the relative magnitude of all stress components must be considered simultaneously, so while the Sxz
profiles are similar for the anisotropic flow relations considered significant here, differences in the Szz
profiles allow the flow relations to be distinguished. The lowest-magnitude Szz
values are predicted by the B2013 and then CAFFE flow relations. Through the collinearity of the and
S
components in these relations, the high levels of shear flow enhancement in the zone from ∼550 m to ∼1100 m, where shear strain rates are highest, contribute directly to reducing the magnitude of Szz
necessary to drive the observed ![]() . Based on a comparison of the anisotropic flow relations using data from laboratory ice deformation experiments conducted in combined simple shear and confined vertical compression, the B2013 and then CAFFE flow relations provided the most realistic stress estimates. In the CAFFE flow relation, grains less favourably aligned for basal shear decrease the macroscopic deformability, leading to a corresponding reduction in the scalar enhancement factor, which increases the magnitude of Szz
, compared with the B2013 estimates.
. Based on a comparison of the anisotropic flow relations using data from laboratory ice deformation experiments conducted in combined simple shear and confined vertical compression, the B2013 and then CAFFE flow relations provided the most realistic stress estimates. In the CAFFE flow relation, grains less favourably aligned for basal shear decrease the macroscopic deformability, leading to a corresponding reduction in the scalar enhancement factor, which increases the magnitude of Szz
, compared with the B2013 estimates.
Throughout the shear-dominated zone at the DSS site, values of the Sxz/Szz ratio for the AGA and TNNI relations are significantly lower than the B2013, CAFFE and Reference GlenGlen (1958) values. These low Sxz /Szz values are indicative of incomplete rheological descriptions, that lead to overestimates of Szz in combined stress configurations where shear is dominant. This view is supported by an analysis of the flow relations using data from combined stress experiments.
The results for the AGA and TNNI flow relations demonstrate that while orientation relationships between crystal c-axes and the applied stresses are important to polycrystalline ice rheology, other processes, particularly those occurring at grain boundaries, play a role in determining the anisotropy and magnitude of deformation rates. These results indicate that in descriptions of polycrystalline rheology based on the description of grain-scale processes, all relevant micro-deformation, recrystallization and recovery mechanisms must be adequately described or paramaterized to produce realistic flow predictions.
The greater emphasis on the parameterization of key rheological variables in the B2013 and CAFFE relations leads to less complex flow descriptions that may be more easily incorporated into ice-sheet models. In particular, the direct relationship between anisotropy and the tertiary-creep flow regime in the B2013 flow relation eliminates the requirement for explicit consideration of crystal c-axis orientations. This greatly simplifies its requirements for implementation in numerical ice-sheet models.
Acknowledgements
This work is supported by the Australian Government Cooperative Research Centres Programme, through the Antarctic Climate and Ecosystems Cooperative Research Centre (ACE CRC), and the by Australian Antarctic Science Program through AAS project 4289. We thank Ed Waddington, an anonymous reviewer and the scientific editor, Sérgio H. Faria, for detailed comments which improved the manuscript.











