Introduction
A large number of mass-balance reconstructions since the beginning of the century have been based on statistical relations or positive degree-day models from nearby meteorological station temperatures and precipitation data (Reference Kodakov,Kodakov, 1966; Reference Martin,Martin, 1977; Reference Dyurgerov, and Popovnin.Dyurgerov and Popovnin, 1980; Reference Tangborn,Tangborn, 1980; Reference Tvede, and Tvede,Tvede, 1982; Reference Gelbert,Gelbert, 1986; Reference Letréguilly,Letré-guilly, 1984; Reference Chen, and FunkChen and Funk, 1990). Generally, only mean monthly data are available and these studies give a linear relation, resulting from statistical analysis, between mass balance and summer temperatures and winter precipitation or annual precipitation
Most of these studies show a very good correlation; Reference Martin,Martin (1977) explained 77% of the Sarennes mass-balance variance with three parameters over a 27 year period; Reference Chen, and FunkChen and Funk (1990) explained 72% of the Rhonegletscher mass-balance variance with two parameters over a 28 year period.
Some of these correlations cover a very short time period and Reference Gelbert,Gelbert (1986) has found that periods of 5 – 10 years are insufficient to establish a reliable relationship giving unchanging explainable variables and stable regression coefficients.
On the other hand, the relations established for glacier d’Argentière in Mont Blane (Reference Vallon,, Vincent and ReynaudVallon and others, 1995) over 18 years, show a mass-balance explained variance percentage that is low, between 38% and 66% depending on the site.
For reconstruction over the past century, it seems important to test the stability of the statistical relation over time. The question is: are these relationships reliable enough for a long-term time-scale extrapolation and what are the constraints on the use of these models?
For this purpose, the Sarennes mass-balance—meteorological data relation (Reference Martin,Martin, 1977) has been reviewed and applied to the recent period. All the observations (1949 – 94) reported by Reference Valla,F.Valla (1989, Reference Valla,unpublished) have been incorporated in this new analysis.
Mass-Balance — Meteorological Data Relations from Sarennes Measurements
Glacier de Sarennes is a small glacier. located in the Grandes Rousses range, in the French Alps (45 °10′ N, 6 °10′ E). It covers an area of about 0.8 km2 between 2800 and 3150 m a.s.l. The mass balance has been measured since 1949 (Reference Valla,Valla, unpublished) from five or six ablation stakes, or drilling core when snow covered the glacier surface.
The Drift in Correlation Since 1973
Following the Reference Martin,Martin (1977) analysis, mass-balance analyses using the Lyon meteorological data relation have been applied to the recent period: the correlations have been determined for two periods (1950 – 70 and 1971 – 91) with two variables (summer temperature and winter precipitation). Surprising results have been obtained (Table 1).
Table.1. Sarennes mass-balance variance partly explained by Lyon – Bron meteorological data fluctuations

For the period 1950 – 70, the Martin mass-balance meteorological data relationship can be recognized but this relation disappears for the next period 1971 – 91. It is encouraging to see the increased precipitation variability imprint between 1971 and 1991 but it is surprising to see an important correlation decrease between snow/ice ablation and summer temperature although temperature variability is similar for both periods.
The comparison of the cumulative observed balances and cumulative balances calculated by Martin’s relation (Fig. 1) seems to show that the fluctuations of the calculated balances are smoothed. This relation attenuates the variations around a mean value. This phenomenon is particularly visible during the years of gain (1977 – 83) and during the years of loss (1985 – 90). These discrepancies raise doubts over the predictive power of such a relation.

Fig. 1. Sarennes cumulative specific net balance since 1949: measurements and Martin relation.
Moreover, it can be noticed that the criterion used by-Martin (balance regression (b) for the temperatures (θ) and/or the precipitation (P)) gives a lower regression co-efficient than the one which would correspond to the axis of symmetry of the group of points (b, θ) or (b, P). Therefore, the extrapolation of the relation outside the data domain gives an appreciable deviation.
Summer ablation and temperatures have been analysed in detail: for exact summer ablation observation periods, the cumulative positive degree-days have been calculated using daily Lyon – Bron temperature data and a temperature gradient fixed at 0.6 ° C/100 m. Therefore, summer ablation and cumulative positive degree-days can be compared over the same time intervals.
A fall in correlation coefficient is found around 1973 (Fig. 2). From 1974, this statistical relation has largely deteriorated: the strong contribution of the temperature changes to the summer ablation between 1949 and 1973 (80% explained ablation variance) becomes negligible between 1974 and 1991 (30% explained ablation variance).

Fig. 2. Explained Sarennes ablation variance with Lyon – Bron cumulative summer temperature ( only daily temperatures above 17.5 ° C are cumulated because of the temperature gradient).
What Triggers such a Phenomenon?
Is it linked to the mass-balance measurement method? Is it connected to the development of ski resorts on this glacier? Is it linked to the quality of meteorological data? Does it re-open the whole question of empirical summer temperature ablation relation reliability? (This relation is not a causality relation, since both terms are distinct surface-energy balance results.)
First, Lyon Bron summer temperature data have been tested from other meteorological stations (Saint Martin d’Hères 1973 – 91 and Lus la Croix Haute 1961 – 94.) These comparisons do not show discrepancies.
Secondly, the glacier de Sarennes measurements have been questioned; these measurements have been compared with the St Sorlin measurements (this glacier is located in the same range, 5 km away). For St Sorlin, long-term summer ablation measurements are not available but mass balance in the ablation zone has been measured since 1956. From these data, mass-balance variations from the mean (centred mass balance) have been calculated according to Reference Lliboutry,Lliboutry’s (1974) model and compared with the Sarennes data (Fig.3).

Fig. 3. St Sorlin and Sarennes centred specific net balance since 1956.
Small corrections on the St Sorlin data (less than 60 cm) have previously been made using the positive degree-day model to take account of the difference between measurement dates. Mass-balance fluctuations of these glaciers are highly correlated, with 84% of the variance being in common (σ = 31cm), and there is no reason to question the quality of the Sarennes measurements.
Lastly, one might think that a realistic relation should take into account the variations of the albedo during the season. In fact, it has been noted that the surface albedo of the small glacier de Sarennes varies greatly during the summer from year to year. In 1976, the glacier had no snow right from the end of June. In 1977, 1978 and 1980, ice never appeared during the whole summer. For each year, we have estimated the date with the balance equal to zero, using the measurements repeated during the summer (Reference Valla,Valla, unpublished). We have distinguished two periods, a snow-ablation period and an ice-ablation period, and established two relationships using the summer temperatures (Figs 4 and 5).These relations are very satisfactory (63.5% explained snow- ablation variance and 87.5% explained ice-ablation variance) and they do not deteriorate over time. In addition, these relations are improved even more when only one point of measurement is chosen on the glacier (because the surface of the glacier may be covered at the top and exposed at the bottom). The relation between snow ablation and summer temperature is not as good as the one for ice. This can be understood for several reasons:
The accumulation measurements, which were made with drill cores, are more delicate than the ablation measurements, since it is not always easy to identify the layer of the previous summer.
The accuracy of the density measurements is mediocre and given the numerous aberrant density values, it is preferable to set the density value at 0.5 for all the accumulation measurements.

Fig. 4. Summer snow ablation expressed as a function of cumulated temperature; cumulated temperature is the sum of temperatures higher than 16.5 ° C at Lyon – Bron (positive degree-day at Sarennes with a fixed temperature gradient of 0.6 ° C km−1). The relation is satisfactory (63.5% explained snow-ablation variance) only due to 1976 and 1983

Fig. 5. Summer ice ablation expressed as a function of cumulated temperature (87.5% explained ice-ablation variance).
Whatever the above relation, in the light of the results, the correlation fall observed from 1973 can now be understood: it is connected to the surface albedo. The ablation/degree-day coefficient value is all the higher when the albedo value is low; furthermore, these results are very close to those drawn from observations on a few Norwegian glaciers (Reference Laumann, and ReehLauman and Reeh, 1993).
During the past two decades, not only has the Variability of summer temperatures and winter precipitation increased (Figs 6 and 7) but the intra-annual seasonal rhythms have been very contrasted: exceptional seasons may succeed one another and this has been the case for the following years:


Fig. 6. Lyon – Bron summer mean temperature (June – September) since 1950. Only temperatures higher than 6.5 ° C are concerned (because of the temperature gradient).

Fig. 7. Lyon – Bron winter precipitation (October – May) since 1950. Only precipitation with temperatures below 16.5 ° C is concerned.
Over the first two decades, the snow ablation remains within a limited range (−1 to −2.2 m of water) and this group of points (Fig. 4) has actually little effect on the regression slope, i.e. on the ablation/degree-day coefficient:
On the one hand, the correlation is mediocre, since the accumulation variability is low for this period (33% explained variance between 1949 and 1973).
On the other hand, and it is also a consequence, this low correlation between snow ablation and temperature does not contradict the ice ablation-temperature relationship.
Over the past two decades, by contrast, the variability in winter precipitation is very high (thanks to the very dry-winter of 1976 and the very rainy winter of 1983). Thus, the snow ablation-temperature relationship is strong and contrasts with the ice ablation/degree-day coefficient. In order to clarify the differences of the surface conditions between 1949 and 1994, the snow-ablation periods and the ice-ablation periods during the summer are shown in Figure 8.

Fig. 8. Duration of snow- and ice-ablation periods at Sarennes (stake 3).
The variability of the duration of these different periods is as follows:

Reconstruction of Summer Ablation
Based on the daily Lyon – Bron meteorological data, the initial and final dates of the ablation season and two ablation/degree-day coefficients, one for the snow (3.8 mm ° C−1J−1) and one for the ice (6.2 mm ° C−1J−1), the summer ablation has been reconstructed by either of two means:
-
(i) Introducing the date when the balance was equal to zero. The explained variance percentage is 68.4% between measured data and reconstructed data, the standard deviation for the ablation is 0.6 m (Fig. 9).
-
(ii) Determining this date through calculation, when the snow ablation is equal to the winter accumulation measured on Sarennes (R2 = 58%), σ = 0.6 m) (Fig. 10).

Fig. 9. Measured summer snow and ice and reconstructed ablation (zero mass-balance date is known) for stake 3. 68% of the variance is explained.

Fig. 10. Measured summer snow and ice and reconstructed ablation (zero mass-balance date is unknown) for stake 3. 58% of the variance is explained.
Accumulation: Winter Precipitation Relationship
One of the biggest difficulties for the reconstruction of the balances using meteorological data concerns the accumulation data. Figures 12,13,14 and 15 show the winter precipitation recorded at different meteorological stations:
Besse en Oisans, a few kilometres from glacier de Sarennes, at an elevation of 1400 m (data from Electricité de France, Grenoble).
Bourg d’Oisans, a few kilometres from Sarennes, at an elevation of 700 m (EDF Grenoble data).
Lyon – Bron, 120 km from Sarennes, in the Rhône Valley, at an elevation of 200 m (Météo France data).
Lus la Croix Haute, 50 km from Sarennes, at an elevation of 1000 m (Météo France data).
Chamonix, 100 km from Sarennes, at an elevation of 1000 m, at the bottom of the Mont Blanc massif (Météo France data).

Fig. 12. Winter precipitation (October – May) at Besse en Oisans and at Lus La Croix Haute (m water). Only 61% of the variance is explained.

Fig. 13. Winter precipitation (October – May) at Besse en Oisans and at Chamonix (m water). Only 79% of the variance is explained.

Fig. 14. Winter precipitation (October – May) at Besse en Oisans and at Bourg d’Oisans (m water). Only 86% of the variance is explained.

Fig. 15. Measured winter accumulation at Sarennes and Lyon-Bron precipitation (October – May). Only rainy days with temperatures below 16.5 ° Care concerned.
It is reassuring to see that the winter precipitation between Besse and Bourg d’Oisans, a few kilometres from each other, is very well correlated. But it is surprising to see that the winter precipitation between Besse and Chamonix, 100 km from each other, is also well correlated!
These comparisons also show the limitations of using meteorological variables taken from very distant stations which are situated in a non-mountainous region. Winter precipitation of Lyon-Bron appears to bear little relation to Besse precipitation (Fig, 11). Since the nearest meteorological stations to Sarennes, Besse and Bourg d’Oisans, are very well correlated (correlation coefficient: 0.93), we have chosen the longer of these two precipitation series (Besse) to put it in relation to Sarennes accumulation (Fig. 16). Figure 15 represents Sarennes accumulation with respect to winter precipitation of Lyon – Bron, in order to show the mediocrity of this relation. By excluding the years 1976, 1977 and 1983, we could even say that there is no relation at all.

Fig. 11. Winter precipitation (October-May) at Besse en Oisans and at Lyon-Bron (m water). Only 25% of the variance is explained.

Fig. 16. Measured winter accumulation at Sarennes (stake 3) and Besse en Oisans precipitation (October – May). Only rainy days with temperatures below 16.5 ° C at Lyon are concerned. 56% of the variance is explained.
Reconstruction of the Accumulation, Ablation and Mass Balance
With the help of the statistical results above, these three terms have been reconstructed based on the following degree-day model:
winter accumulation = 2.40 PBresse(oct – May)
+ 0.13 m of water ablation = -6.2 × 10−3
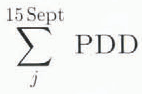 PDD
PDD
where j is 3.78 × 10−3
 PDD = winter accumulation.
PDD = winter accumulation.
(PDD is positive degree-day (Lyon – Bron temperature) and the day j is the day when the ice appears.)
The temperature data used are those from Lyon – Bron (we do not have long series of daily temperatures close to the glacier). The winter precipitation data used are those from Besse en Oisans. Figure 17 shows the values for the balances reconstructed in the manner outlined above, the observed balances and the extreme values of the balances reconstructed by applying to the model an error of ±0.5 m of water for both the accumulation and the ablation values.

Fig. 17. Measured and reconstructed specific net balance of glacier de Sarennes. The thin lines show the extreme values of the balances by applying to the model an error of 0.5 m of water for both the accumulation and ablation values.
The two curves are relatively well correlated (ρ = 0.81). There are big differences between the measured values and the calculated values only for a few years, such as 1983. That was a year with exceptional amounts of snow (Fig. 16), which is poorly represented by Besse en Oisans precipitation.
Conclusions
This paper shows the limits of mass-balance reconstruction drawn from meteorological data. In particular, the relation of the Sarennes balance, apparently strongly established over an observation period of more than 20 years (1949 – 74), is no longer the same over the past two decades (1974 – 94). More precisely, we have shown that the strong relationship between summer temperature and summer ablation between 1949 and 1974 completely deteriorated over the past 20 years.
By taking into account the state of the glacier surface (snow-ice) during successive summers, we have highlighted the importance of the albedo and the necessity to distinguish snow ablation from ice ablation. For small glaciers like glacier de Sarennes, whose whole surface is close to the equilibrium line, it is impossible to ignore this parameter. As far as large glaciers are concerned, the inter-annual changes of surface conditions probably play a less important role in the total ablation variations, since they only modify that part close to the equilibrium line.
In order to take into account the conditions of the glacier surface, reconstruction requires daily meteorological data and not only monthly data. Furthermore, for a reliable reconstruction, it seems important to check global volume variation by another method (cartographic means).
Acknowledgements
We should like to thank all those who collected data from St Sorlin and Sarennes over a long period, and especially, L. Reynaud and F. Valla. We should also like to express our gratitude to Μ. Tourasse and Μ. Debrieux, Grenoble DTG (Electricité de France), who gave us permission to use meteorological data from Besse en Oisans and Bourg d’Oisans.




















