Introduction
Since the early 1970s (Reference HughesHughes, 1973; Reference WeertmanWeertman, 1974), it has been recognized that marine ice sheets grounded below sea level may be unstable to small climate perturbations, particularly when the ice-sheet bed slopes down towards the interior of the ice sheet (Reference WeertmanWeertman, 1974; commonly termed a ‘negative bed slope’). With much of the West Antarctic ice sheet (WAIS) in such a configuration (e.g. Reference FretwellFretwell and others, 2013), there has long been widespread concern regarding the future of the WAIS and the amount of sea-level rise that would result from such loss of ice (Reference MercerMercer, 1978; Reference Mitrovica, Tamisiea, Davis and MilneMitrovica and others, 2001, Reference Mitrovica, Gomez and Clark2009; Reference Alley, Clark, Huybrechts and JoughinAlley and others, 2005; Reference Bamber, Riva, Vermeersen and LeBrocqBamber and others, 2009). This concern has grown steadily with time, culminating with a number of observations within the last year that demonstrate inevitable ice loss due to negative bed slopes in various regions of Antarctica (Reference FavierFavier and others, 2014; Reference Joughin, Smith and MedleyJoughin and others, 2014; Reference Mengel and LevermannMengel and Levermann, 2014; Reference Rignot, Mouginot, Morlighem, Seroussi and ScheuchlRignot and others, 2014).
Interest in ice-sheet stability has also prompted a number of theoretical investigations on the topic, starting with Reference WeertmanWeertman (1974) and more recently Reference Hindmarsh and Le MeurHindmarsh and LeMeur (2001), Reference WilchinskyWilchinsky (2001) and Reference SchoofSchoof (2007a). Although Reference Hindmarsh and Le MeurHindmarsh and LeMeur (2001) suggest neutral stability for a wide range of conditions, all of the other analyses predict that negative bed slopes at the grounding line (where the ice sheet reaches flotation and becomes an ice shelf) result in unstable ice sheets, whereas positive bed slopes (sloping down towards the ocean) are stable. In all of these analyses, except Wilchinsky’s, the ice sheet is assumed to slide on bedrock with a nonlinear power-law relationship between velocity and stress. Alternatively, Wilchinsky’s no-slip basal boundary condition can be thought of as an end-member case of the power-law relation. As such, none of these previous studies incorporate more general basal conditions, such as Coulomb friction behavior, which is thought to be applicable near the grounding line (Reference Iverson, Hooyer and BakerIverson and others, 1998; Reference Tulaczyk, Kamb and EngelhardtTulaczyk and others, 2000a; Reference SchoofSchoof, 2006).
The goal of this work is to address how the inclusion of both power-law basal stress and Coulomb friction dynamics modifies ice-sheet behavior. We take Reference SchoofSchoof’s (2007a) model as a starting point and provide side-by-side comparisons of our results throughout the text. We begin with a review of the traditional power-law assumption and the evidence for a Coulomb friction regime. Next, we provide an approximate analysis for the modified ice-sheet surface profile in the Coulomb case, which is then followed by a numerical calculation of the full stress balance. We find that the profiles differ substantially between the power-law and Coulomb cases near the grounding line. The change in the stress balance here results in a Coulomb boundary layer with different dependence on physical parameters than in the power-law case, and we discuss the implications for ice-sheet stability. Finally, we find that it is possible to arrive at the grounding-line ice-flux scalings in both the power-law and Coulomb cases via a simpler derivation using insights from the boundary-layer behavior.
The Traditional Power-Law Basal Rheology
We first introduce the power-law basal rheology, as well as the important implications of using this assumption. This standard power-law assumption on the basal boundary condition at the bed of an ice sheet can be written as
where u b is the basal velocity, C is a constant, τ b is the basal shear stress and m is usually related to the Glen’s flow law exponent, n (Reference GlenGlen, 1952). For example, in Weertman’s classic analysis of glacial sliding (Reference WeertmanWeertman, 1957), he finds that m = 2 when n = 3 due to competition between regelation and enhanced basal viscous ice flow. Other authors assume m ≈ 3 (e.g. Reference WeertmanWeertman, 1974; Reference SchoofSchoof, 2007a). Due to our later comparisons with Schoof’s results, it is worth noting that Schoof’s m is defined as the reciprocal of the m defined here, i.e. m Schoof ≡ 1/m ≈ 1/3.
A common approximation to the full-Stokes model of glacier flow, called the shallow-ice-stream approximation (SSA) or shallow-shelf approximation (Reference Bueler and BrownBueler and Brown, 2009), is particularly applicable to ice sheets near grounding lines, where the deformation of ice is responsible for a small fraction of the ice velocity (e.g. Reference SchoofSchoof, 2007a). Under the SSA, the vertically integrated stress balance in one horizontal dimension (1-HD) can be written as
where A and n are the standard rate factor and exponent in Glen’s flow law, u is the ice velocity, h is the ice-sheet thickness, b is the depth of the sea floor, ρ is the ice density, g is the gravitational acceleration, x is a horizontal coordinate and the strain rate, ∂u = ∂x ≡ ux
, is assumed to be positive (Reference SchoofSchoof, 2007a). (With negative strain rates, the term ![]() should be written as |ux
|1/n−1
ux
, but negative strain rates are not found in any numerical solutions, so we omit the absolute values for simplicity.) We refer to the three terms in Eqn (2) (from left to right) as the extensional stress term (or extensional stress divergence), the basal drag and the driving stress (Fig. 1). We also note that if internal ice deformation is assumed small, which is appropriate for ice streams near the grounding line, then u ≈ u
b and τ
b = C
1/m
u
1/m
, so the only unknowns in Eqn (2) are h and u.
should be written as |ux
|1/n−1
ux
, but negative strain rates are not found in any numerical solutions, so we omit the absolute values for simplicity.) We refer to the three terms in Eqn (2) (from left to right) as the extensional stress term (or extensional stress divergence), the basal drag and the driving stress (Fig. 1). We also note that if internal ice deformation is assumed small, which is appropriate for ice streams near the grounding line, then u ≈ u
b and τ
b = C
1/m
u
1/m
, so the only unknowns in Eqn (2) are h and u.
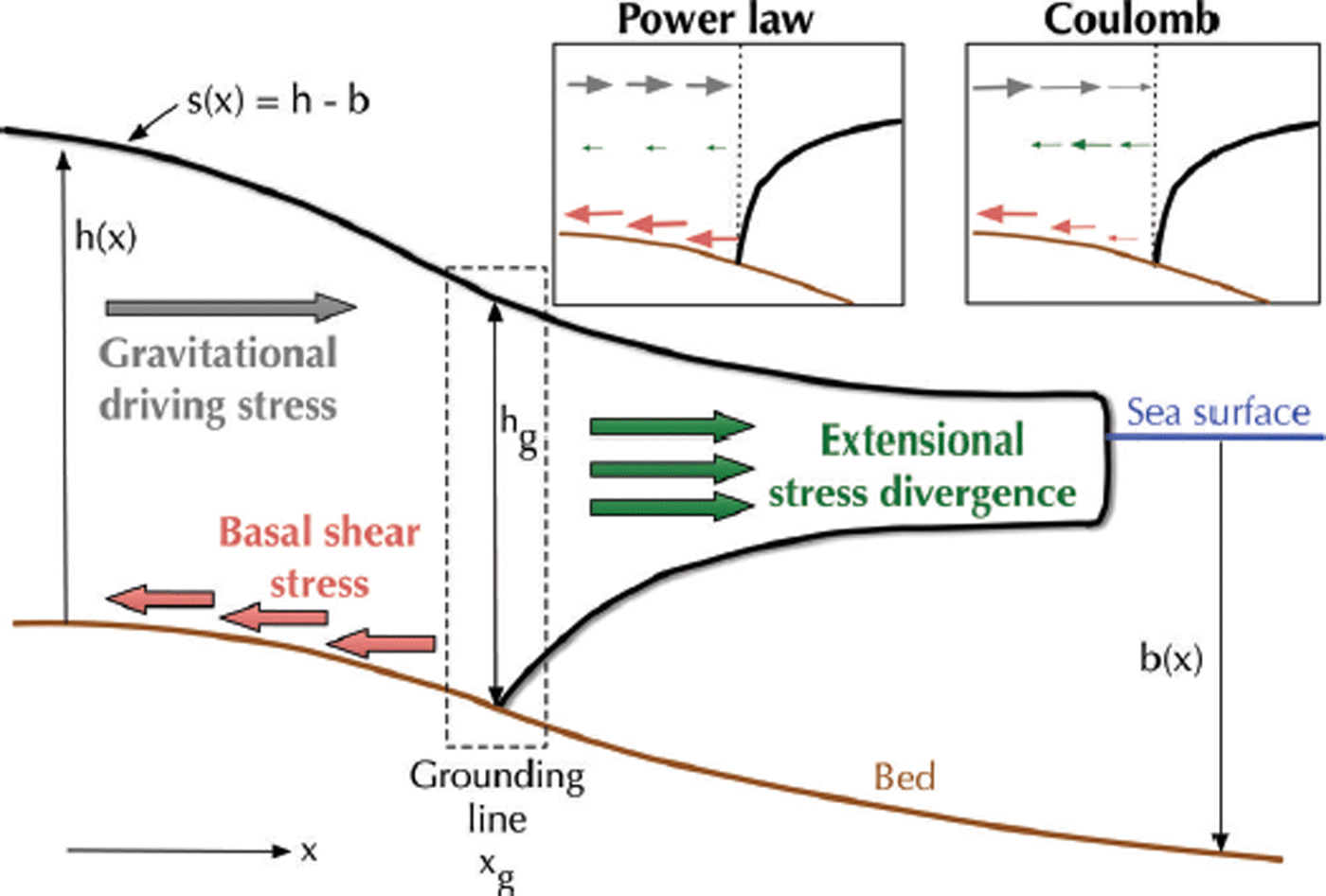
Fig. 1. Schematic of the one-horizontal-dimension ice-sheet model. The three terms of the governing force balance (Eqn (2)) are the extensional stress divergence term (green), the basal shear stress (or basal drag; red) and the gravitational driving stress (gray). The grounding line is where the ice sheet transitions into an ice shelf and therefore reaches flotation. The two insets schematically depict the approximate magnitudes of the three stress terms in the power-law case (left inset) and Coulomb case (right inset).
The shallow-ice approximation (SIA) stress balance can be obtained simply by deleting the extensional stress term, leaving a balance between basal drag and driving stress. In the SIA framework, a particularly simple solution for the ice-sheet profile, h(x), can be derived when the perfectly plastic approximation to Eqn (1) is assumed. This approximation corresponds to the limit m → ∞, resulting in u b = 0 below a yield stress, τ 0, and arbitrarily high velocities above the yield stress. With zero basal slope, bx ≡ 0, the stress balance in Eqn (2) reduces to
and an ice-sheet profile may be derived by integration (e.g. Reference NyeNye, 1951; Reference WeertmanWeertman, 1974) as
i.e. the classical parabolic ice-sheet profile, where H is the maximum height of the ice sheet (at x = 0). Note that this classic result will be compared with our approximate profiles in a later section.
Reference SchoofSchoof (2007a) showed that the SSA with the power-law basal rheology of Eqn (1) can be used to derive not only steady-state ice-sheet profiles, but also stability criteria for the grounding line. The system of equations is closed by adding continuity and boundary conditions. Ice mass conservation can be written as ht + (uh) x = a, where a is ice accumulation and t is time, and the boundary conditions at the ice-sheet interior are (h − b) x = 0 and u = 0. The boundary conditions at the grounding line, x = x g, are
where ρ
w is water density, h
f is the local ice thickness at flotation and ![]() denotes being evaluated at x = x
g. Here xref Eqn (5a) is the flotation condition, and Eqn (5b) ensures continuity with the stresses in the ice shelf (Reference SchoofSchoof, 2007a).
denotes being evaluated at x = x
g. Here xref Eqn (5a) is the flotation condition, and Eqn (5b) ensures continuity with the stresses in the ice shelf (Reference SchoofSchoof, 2007a).
Reference SchoofSchoof (2007a) applied boundary layer theory near the grounding line and found that the flux of ice, q = hu, at the grounding line, x g, can be written as

where the ‘PL’ subscript indicates ‘power law’ and ![]() is the ice-sheet thickness at the grounding line, which is equal to the flotation thickness through Eqn (5a). With n = m = 3, it follows that
is the ice-sheet thickness at the grounding line, which is equal to the flotation thickness through Eqn (5a). With n = m = 3, it follows that ![]() . This strong dependence of grounding-line flux on grounding-line ice thickness implies that the grounding line is stable for ‘positive’ bed slopes (i.e. sloping down away from the center of the ice sheet, bx > 0, dh
f/dx > 0) and unstable for reverse (‘negative’) bed slopes. This argument can be summarized as follows: If grounding-line flux is an increasing function of h
g and there is a positive bed slope (grounding-line thickness, h
f, increases with x, i.e. dh
f/dx > 0) then dq
g/dx > 0. Thus, if the grounding line retreats, then ice flux decreases, which causes the ice to thicken and therefore advance, stabilizing the system. However, for a reverse slope (dh
f/dx < 0), dq
g/dx < 0 and retreat of the grounding line causes an increase in flux, thinning, and thus further retreat, i.e. a positive feedback. This qualitative argument has been found to be quantitatively accurate (Reference SchoofSchoof, 2012).
. This strong dependence of grounding-line flux on grounding-line ice thickness implies that the grounding line is stable for ‘positive’ bed slopes (i.e. sloping down away from the center of the ice sheet, bx > 0, dh
f/dx > 0) and unstable for reverse (‘negative’) bed slopes. This argument can be summarized as follows: If grounding-line flux is an increasing function of h
g and there is a positive bed slope (grounding-line thickness, h
f, increases with x, i.e. dh
f/dx > 0) then dq
g/dx > 0. Thus, if the grounding line retreats, then ice flux decreases, which causes the ice to thicken and therefore advance, stabilizing the system. However, for a reverse slope (dh
f/dx < 0), dq
g/dx < 0 and retreat of the grounding line causes an increase in flux, thinning, and thus further retreat, i.e. a positive feedback. This qualitative argument has been found to be quantitatively accurate (Reference SchoofSchoof, 2012).
Coulomb Friction as an Alternative to Power-Law Basal Rheologies
The goal of this work is to demonstrate how some of the previous conclusions derived when using a power-law basal rheology are modified when complemented by Coulomb friction. Specifically, we compute revised ice-sheet profiles and the associated stresses, and provide an ice-sheet stability analysis in the form of a modified Eqn (6). Prior to these calculations, however, we briefly describe the evidence for Coulomb friction, the importance of using such a description, our specific quantitative modification to Eqn (1), and the likely regions of applicability.
While the use of power-law basal rheologies in glacier modeling has a long history (e.g. Reference Boulton and HindmarshBoulton and Hindmarsh, 1987; Reference MacAyealMacAyeal, 1989), more recent experimental evidence suggests that glacial tills are often better described by a Coulomb plastic rheology (Reference Iverson, Hooyer and BakerIverson and others, 1998; Reference Tulaczyk, Kamb and EngelhardtTulaczyk and others, 2000a; Reference Truffer, Echelmeyer and HarrisonTruffer and others, 2001). In this case, basal shear stress is proportional to the effective pressure, σ n, or
Here f is a friction coefficient (typically f ≲ 0.6), σ 0 = ρgh is the ice pressure, p = ρwgb is the water pressure, other symbols are as before, and the till is assumed cohesionless and hydrostatically connected to the ocean. While power-law basal rheologies have been proposed that include the effective pressure dependence in an ad hoc manner (e.g. Reference PatersonPaterson, 2002), the Coulomb law naturally has an effective pressure dependence, due to the fact that friction is only supported by the pressure on solid contacts. The predicted difference between the Coulomb law of Eqn (7) and the power law of Eqn (1) is especially large near the grounding line, where the Coulomb law predicts basal shear stresses that approach zero (since σ n → 0), whereas Eqn (1) predicts the largest basal shear stresses there, because velocities are greatest. Importantly, even in the ‘plastic’ case of Eqn (1), where m → ∞ and there is a constant yield stress, the two predictions are distinctly different, due to the effective pressure dependence of the Coulomb law. Finally, since Coulomb friction limits shear stresses in a till layer that lies underneath the basal layer where the power-law rheology applies, both mechanisms may act to limit shear stresses. To accommodate both mechanisms, we set the basal shear stress to the minimum of the two stresses, i.e.
Note that the form of Eqn (8) is common to any system where stresses are limited by two independent physical mechanisms (e.g. Reference Brace and KohlstedtBrace and Kohlstedt, 1980).
From this combined basal stress law, it is clear that τ b must obey the Coulomb law sufficiently near the grounding line, where fσn → 0. The power-law applies sufficiently far upstream of the grounding line, where the ice sheet is thick enough (i.e. σ 0 is large enough) that the Coulomb term is no longer important. To estimate where this transition occurs, we note that the power-law rheology can be approximated with its (m → ∞) yield stress, τ 0, which Reference PatersonPaterson (2002) suggests is ∼100 kPa. Thus, we can expect the crossover from Coulomb to power-law roughly when f ρg(h − h f) ≳ 100 kPa, or h − h f ≳ 17 m. While this difference in ice-sheet height is quite small, implying a narrow Coulomb regime in many cases (except when the thickness gradient is small, as with ice plains, which can have surface slopes less than 10−4), we will show that the transition to Coulomb behavior near the grounding line still results in significant modification of both the ice-sheet profile and ice-sheet stability criteria.
While the Coulomb basal rheology has been used in a limited number of glaciological studies, including the ice-stream model of Reference Tulaczyk, Kamb and EngelhardtTulaczyk and others (2000b), the theoretical treatment of Reference SchoofSchoof (2006) and the numerical glacier models of Reference Truffer, Harrison and EchelmeyerTruffer and others (2000) and Reference Bueler and BrownBueler and Brown (2009), none of these studies specifically address the question of ice-sheet profiles near the grounding line or the differences in stability criteria that result from the modification of stresses in this region. We focus on these points, and highlight the importance of the Coulomb modification for understanding grounding-line behavior, even in the absence of other physics. Our analysis closely follows the one-horizontal-dimension (1-HD) theory of Reference SchoofSchoof (2007a), and therefore has the same limitations of not including buttressing or other more complex geometric dependencies of less-idealized ice-sheet models (e.g. Reference Gudmundsson, Krug, Durand, Favier and GagliardiniGudmundsson and others, 2012; Reference PattynPattyn and others, 2013). Nonetheless, the model predicts novel ice-sheet behavior that needs to be understood before adding more complex modifications.
Approximate Ice-Sheet Profiles Under Coulomb Sliding
In this section we explore some of the consequences of the Coulomb modification of Eqn (8) under the simplifying assumption of a balance between the driving and basal stresses (e.g. Reference WeertmanWeertman, 1974). Though our later analysis shows that extensional stress is also important close to the grounding line, it is instructive to consider this approximate stress balance, because its solutions may be more readily understood and provide additional insight into the grounding-line behavior. As discussed above, close to the grounding line the basal stress must transition from a power-law drag to Coulomb friction, and in this region the basal stress is described by Eqn (7). Neglecting the extensional stress term in Eqn (2), the stress balance therefore becomes
Equation (9) is approximately valid for an ice sheet that is completely buttressed by its ice shelf, in which case the extensional stress vanishes at the grounding line (Reference Dupont and AlleyDupont and Alley, 2005; Reference SchoofSchoof, 2007b); the results of this section apply exactly in this special case.
An immediate consequence of Eqn (9) is that at the grounding line, where h = h
f, the slope of the ice sheet’s upper surface, s = h − b, must be zero. To determine how the ice sheet adjusts to such a condition, we first simplify Eqn (9) via a change of variables that describes its behavior close to the grounding line. First we write the distance relative to the grounding line as ξ = x − x
g, such that h
g = h
f|
ξ
=0, and we assume a locally constant bed slope, such that b = (ρ/ρw
)h
g + βξ. Then we rearrange Eqn (9) as a differential equation for ![]() , the surface height relative to the grounding-line surface height, s
g = h
g − b|
ξ
=0 = h
g(1 − ρ/ρ
w),
, the surface height relative to the grounding-line surface height, s
g = h
g − b|
ξ
=0 = h
g(1 − ρ/ρ
w),

Here, for convenience, we define a relative density parameter,
Similar to Reference WeertmanWeertman’s (1974) stress balance (Eqn (3)), Eqn (10) is an ordinary differential equation for surface height as a function of horizontal position. Unlike Eqn (3), however, Eqn (10) cannot, in general, be solved analytically, but we may obtain approximate solutions in certain limits.
First we consider the case of a vanishingly small bed slope (β → 0), as in Reference WeertmanWeertman’s (1974) parabolic solution, given by Eqn (4). For small excursions of the surface height, ![]() , Eqn (10) can be rewritten approximately as
, Eqn (10) can be rewritten approximately as

The analytical solution is ![]() , implying an exponential decay of the ice surface towards the grounding line. This differs substantially from the parabolic profile of Eqn (4) for a constant basal shear stress. Here the ice-sheet profile ‘tapers off’ toward the grounding line, instead of maintaining a steep surface slope. We show later that the inclusion of extensional stresses quantitatively changes this profile. However, the qualitative differences between the Coulomb case and the power-law-only case are the same and hence this approximate result provides a useful intuition regarding these differences.
, implying an exponential decay of the ice surface towards the grounding line. This differs substantially from the parabolic profile of Eqn (4) for a constant basal shear stress. Here the ice-sheet profile ‘tapers off’ toward the grounding line, instead of maintaining a steep surface slope. We show later that the inclusion of extensional stresses quantitatively changes this profile. However, the qualitative differences between the Coulomb case and the power-law-only case are the same and hence this approximate result provides a useful intuition regarding these differences.
The case of vanishingly small slope, β, is distinguished in that it cannot satisfy the boundary condition ![]() at the grounding line, ξ = 0; the only solution that can admit zero gradient at the grounding line is zero everywhere. For nonzero slope, the parameter dependence of the solution can be simplified by nondimensionalizing Eqn (10) using
at the grounding line, ξ = 0; the only solution that can admit zero gradient at the grounding line is zero everywhere. For nonzero slope, the parameter dependence of the solution can be simplified by nondimensionalizing Eqn (10) using ![]() and
and ![]() ,
,

where ![]() is a dimensionless friction coefficient and
is a dimensionless friction coefficient and ![]() is either equal to 1 for a positive bed slope or −1 for a negative bed slope. At the grounding line, the surface height perturbation vanishes
is either equal to 1 for a positive bed slope or −1 for a negative bed slope. At the grounding line, the surface height perturbation vanishes ![]() , so we seek a solution close to the grounding line by assuming
, so we seek a solution close to the grounding line by assuming ![]() . We further assume
. We further assume
![]() , so the terms in the numerator of Eqn (13) are asymptotically of the same order, though in reality there is no reason to expect such a relation to hold. At leading order in
, so the terms in the numerator of Eqn (13) are asymptotically of the same order, though in reality there is no reason to expect such a relation to hold. At leading order in ![]() , Eqn (13) becomes
, Eqn (13) becomes

which may be solved analytically to obtain

Note that at the grounding line, ![]() , this solution satisfies the boundary condition
, this solution satisfies the boundary condition
![]() , and additionally that the slope of the ice sheet vanishes,
, and additionally that the slope of the ice sheet vanishes, ![]() , as expected from the stress balance in Eqn (9).
, as expected from the stress balance in Eqn (9).
In Figure 2 we illustrate the shape of the ice sheet close to the grounding line under the stress balance of Eqn (9), and for positive bed slope, ![]() . We plot the dimensionless ice-sheet profile calculated analytically from Eqn (15) and numerically from Eqn (13), along with the bathymetry and the ice-sheet surface height at flotation s
f = h
f − b = (ρ
w/ρ − 1)b. There is relatively little scope for changes in the density parameter, δ, which we fix at δ = 0.1, so the range of possible ice-sheet profiles is essentially defined by the dimensionless friction parameter,
. We plot the dimensionless ice-sheet profile calculated analytically from Eqn (15) and numerically from Eqn (13), along with the bathymetry and the ice-sheet surface height at flotation s
f = h
f − b = (ρ
w/ρ − 1)b. There is relatively little scope for changes in the density parameter, δ, which we fix at δ = 0.1, so the range of possible ice-sheet profiles is essentially defined by the dimensionless friction parameter, ![]() , and the sign of the bed slope,
, and the sign of the bed slope, ![]() . Varying
. Varying ![]() simply expands or squeezes the ice-sheet profile horizontally, relative to the bed, so the characteristics of the solution are summarized by the cases
simply expands or squeezes the ice-sheet profile horizontally, relative to the bed, so the characteristics of the solution are summarized by the cases ![]() and
and ![]() .
.
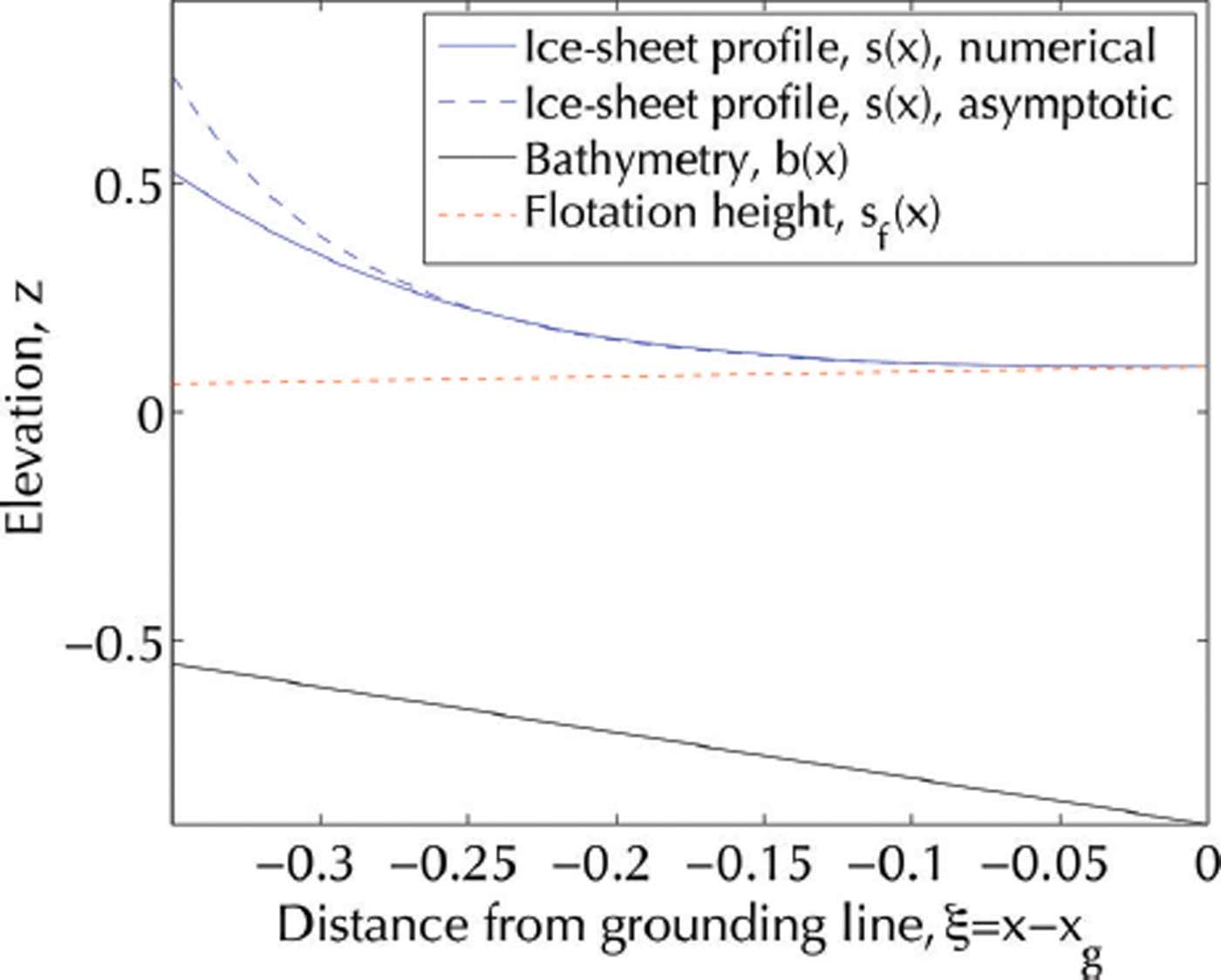
Fig. 2. Near-grounding line ice-sheet profile, prescribed by a balance between driving stress and Coulomb sliding, over linear topography with positive (β > 0) bed slope. We use dimensionless variables to illustrate the qualitative properties of the ice-sheet profile over a range of parameters. Note that we have chosen an unrealistically small Coulomb parameter, ![]() , in order to visualize the curve of the ice-sheet profile and the slope of the bathymetry together. The density parameter is set to δ = 0:1.
, in order to visualize the curve of the ice-sheet profile and the slope of the bathymetry together. The density parameter is set to δ = 0:1.
Figure 2 shows that Coulomb sliding at the bed results in a dramatic alteration of the ice-sheet profile close to the grounding line. The vanishing basal stress results in the ice sheet ‘tapering off’ towards the grounding line, in contrast to the steep surface gradient predicted by a uniform basal stress (Reference WeertmanWeertman, 1974) or power-law drag (Reference SchoofSchoof, 2007a). Another distinguishing feature of Coulomb sliding is that for negative bed slope (β < 0) the solution is unphysical, as the ice sheet lies below flotation everywhere. To understand this, recall that the surface height must have zero gradient at the grounding line, ds/dx = 0 at x = x g, but the gradient of the flotation height, ds f/dx = (ρ w/ρ − 1)db/dx = (ρ w/ρ − 1)β, depends on the sign of β. For the solution to be physical, we require d(s − s f) = dx < 0 at x = x g, so the ice is above flotation just upstream of the grounding line, but this condition is only satisfied for positive bed slope, β > 0. Thus, for a negative bed slope and vanishing extensional stress at the grounding line, the ice sheet cannot ground stably, as no physical steady solutions exist.
Steady-State Ice-Sheet Profiles with Coulomb Basal Conditions
Though the ice-sheet profiles discussed in the previous section provide a qualitative illustration of the effect of Coulomb friction close to the grounding line, the neglect of extensional stress is problematic. Unless the ice shelf is buttressed, the extensional stress must be sufficiently large to balance the driving stress, so we expect the effects of both Coulomb friction and extensional stress to become important close to the grounding line. In this section, we therefore expand our analysis to consider steady solutions of the full, one-dimensional, depth-integrated force balance in Eqn (2).
We begin by nondimensionalizing the force balance in Eqn (2), as this allows us to characterize the range of ice-sheet profiles using a small number of dimensionless parameters. We first select scales for horizontal distance, [x], ice thickness, [h], and ice accumulation, [a]. The steady ice conservation equation, (hu) x = a, motivates a velocity scale [u] = [a][x]/[h], such that in dimensionless variables (denoted by hats, ^) it becomes
For simplicity we have assumed the accumulation rate, a, to be spatially uniform. Substituting these scales into the stress balance (Eqn (2)) with the Coulomb-modified basal rheology of Eqn (8), we obtain
Here we define

as the dimensionless extensional stress coefficient, power-law coefficient and Coulomb friction coefficient respectively. Equations (17a) and (17b) are complemented by no-flux and zero-surface gradient boundary conditions at the upstream edge of the domain ![]() , and by stress continuity and basal flotation conditions (Eqns (5a) and (5b)) at the grounding line. With dimensionless variables, these conditions become
, and by stress continuity and basal flotation conditions (Eqns (5a) and (5b)) at the grounding line. With dimensionless variables, these conditions become


This nondimensionalization almost exactly mirrors that of Reference SchoofSchoof (2007a), except that he sets the power-law coefficient, ![]() , to 1, such that Eqn (18) provides an additional constraint relating the horizontal and vertical scales, [x] and [h].
, to 1, such that Eqn (18) provides an additional constraint relating the horizontal and vertical scales, [x] and [h].
We base the solutions discussed below on ‘typical’ Antarctic ice-sheet scales (Reference SchoofSchoof, 2007b): n = m = 3, [a] = 0.3 m a−1, [x] = 500 k m, [h] = 1 k m, A = 1.0 × 10−25 s−1 P a−3, C1/m
= 7.624 × 106 P a m−1/3 s1/3, ρ = 900 kg m−3, ρ
w = 1000 kg m−3, g = 9.8 m s−2 and f = 0.4. These scales yield dimensionless parameter values of ε ≈ 2.6 × 10−3, δ ≈ 0.1, ![]() and
and ![]() . These scalings suggest that the extensional stress term in Eqn (17a) should be much smaller than the driving and basal stresses, but condition Eqn (19d) requires the extensional stress itself to become
. These scalings suggest that the extensional stress term in Eqn (17a) should be much smaller than the driving and basal stresses, but condition Eqn (19d) requires the extensional stress itself to become ![]() at the grounding line. Reference SchoofSchoof (2007a) argues that this condition is met via the development of a boundary layer close to the grounding line. Meanwhile, the dimensionless Coulomb friction coefficient,
at the grounding line. Reference SchoofSchoof (2007a) argues that this condition is met via the development of a boundary layer close to the grounding line. Meanwhile, the dimensionless Coulomb friction coefficient,
![]() , appears as a very large term in Eqn (17b), whereas the dimensionless power-law coefficient,
, appears as a very large term in Eqn (17b), whereas the dimensionless power-law coefficient, ![]() , is
, is ![]() . As discussed above, this implies that the ice thickness must be very close to flotation, i.e.
. As discussed above, this implies that the ice thickness must be very close to flotation, i.e.
![]() , before the basal stress makes the transition from power-law to Coulomb sliding.
, before the basal stress makes the transition from power-law to Coulomb sliding.
The grounding-line position and stability of this model with power-law-only basal stress has been explored in detail by Reference SchoofSchoof (2007a,b). We therefore focus on the differences introduced by the modified basal stress (Eqn (17b)) that includes Coulomb friction. We obtain steady solutions by first numerically discretizing Eqns (16) and (17) and boundary conditions, Eqns (19a–19d), using second-order centered differences. Following Reference SchoofSchoof (2007a), we stagger the ![]() and
and ![]() gridpoints, such that the first
gridpoints, such that the first ![]() -point coincides with
-point coincides with ![]() and the last
and the last ![]() -point coincides with
-point coincides with ![]() . The gridpoints are uniformly spaced between
. The gridpoints are uniformly spaced between ![]() and
and ![]() , where the grounding-line position,
, where the grounding-line position, ![]() , and thus the grid itself, is allowed to change as the calculation proceeds. Finally, we employ Levenberg–Marquardt nonlinear least-squares optimization (Reference Moré and WatsonMoré, 1978) of the gridpoint velocities and layer thicknesses and the grounding-line position to obtain an optimal steady solution of the equations and boundary conditions. In the cases discussed here, we use Nx
= 4000 gridpoints for each of the
, and thus the grid itself, is allowed to change as the calculation proceeds. Finally, we employ Levenberg–Marquardt nonlinear least-squares optimization (Reference Moré and WatsonMoré, 1978) of the gridpoint velocities and layer thicknesses and the grounding-line position to obtain an optimal steady solution of the equations and boundary conditions. In the cases discussed here, we use Nx
= 4000 gridpoints for each of the ![]() and
and ![]() fields, which is sufficient to make the results insensitive to increased resolution.
fields, which is sufficient to make the results insensitive to increased resolution.
Figure 3 shows ice-sheet surface height and velocity profiles, with and without the Coulomb modification of the basal stress in Eqn (17b). For the purpose of illustration we have selected a simple parabolic bathymetry, ![]() . At the ice-sheet scale (
. At the ice-sheet scale (![]() horizontal scale) the profiles are qualitatively similar, with a parabolic-like thinning of the ice sheet and rapid increase of the ice velocity toward the grounding line. However, with Coulomb friction the position of the grounding line shifts upstream by a dimensionless distance of ∼0.2, equivalent to a dimensional distance of ∼100 km, using the horizontal length scale of [x] = 500 km given above. On our idealized bathymetry this corresponds to grounding-line thickness reduction from 0.648 to 0.472, or from 648 to 472 m using the height scale [h] = 1 km given above. The fractional reduction in grounding-line thickness exceeds the fractional reduction in total accumulation over the ice-sheet surface, resulting in a higher ice velocity at the grounding line. In the next section, we show that this migration of the grounding line is a consequence of the stress balance in the boundary layer, which implies a smaller grounding-line thickness under a Coulomb sliding law.
horizontal scale) the profiles are qualitatively similar, with a parabolic-like thinning of the ice sheet and rapid increase of the ice velocity toward the grounding line. However, with Coulomb friction the position of the grounding line shifts upstream by a dimensionless distance of ∼0.2, equivalent to a dimensional distance of ∼100 km, using the horizontal length scale of [x] = 500 km given above. On our idealized bathymetry this corresponds to grounding-line thickness reduction from 0.648 to 0.472, or from 648 to 472 m using the height scale [h] = 1 km given above. The fractional reduction in grounding-line thickness exceeds the fractional reduction in total accumulation over the ice-sheet surface, resulting in a higher ice velocity at the grounding line. In the next section, we show that this migration of the grounding line is a consequence of the stress balance in the boundary layer, which implies a smaller grounding-line thickness under a Coulomb sliding law.

Fig. 3. (a) Surface profiles and (b) velocities of a steady ice sheet computed using the dimensionless equations given by Eqns (16) and (17) and boundary conditions given by Eqns (19a–19d). The dimensionless parameters, ε ≈ 2.6 × 10−3, δ ≈ 0.1, ![]() and
and ![]() , correspond to the ‘typical’ Antarctic ice-sheet parameters given by Reference SchoofSchoof (2007b). The insets zoom in on the region very close to the grounding line, where the basal stress switches from power-law drag to Coulomb friction.
, correspond to the ‘typical’ Antarctic ice-sheet parameters given by Reference SchoofSchoof (2007b). The insets zoom in on the region very close to the grounding line, where the basal stress switches from power-law drag to Coulomb friction.
The insets in Figure 3 show that Coulomb friction also qualitatively changes the shape of the ice sheet close to the grounding line. Whereas the ice-sheet surface is steepest at the grounding line under power-law drag, with Coulomb friction it tapers off toward the grounding line, similar to the extensional stress-free solution shown in Figure 2. Ice conservation then requires that the velocity profile also tapers off toward the grounding line. The contrast between the solutions close to the grounding line may be understood by considering the different contributions to the stress balance, which are plotted in Figure 4 (Fig. 1 insets show schematics). With power-law drag alone, the extensional stress becomes sufficiently large to satisfy Eqn (19d), but its divergence always remains small compared with the driving and basal stresses, so the expected boundary layer is not apparent in the stress balance. By contrast, with the Coulomb modification to the basal stress in Eqn (17b), there is a rapid enhancement of the extensional stress divergence just beyond the transition from power-law drag to Coulomb friction. This occurs because the basal stress vanishes at the grounding line, and the extensional stress divergence alone must balance the driving stress. Though the ice-sheet profile does not taper to zero surface slope, as suggested by our earlier solution (shown in Fig. 2), the driving stress does decrease by around a factor of 4 across the boundary layer.
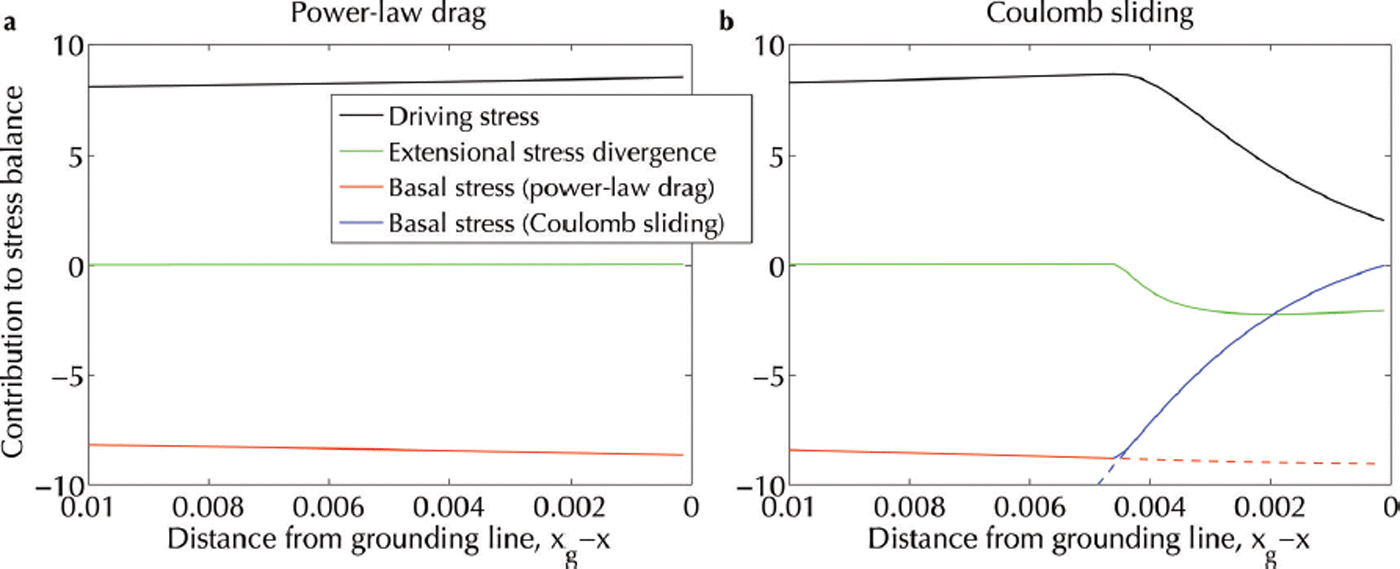
Fig. 4. Terms in the dimensionless stress balance in Eqn (17a) for the ice-sheet solution shown in Figure 3. In each case the plot covers only the region very close to the grounding line. (a) With only power-law drag no boundary layer is evident: the extensional stress divergence remains small all the way up to the grounding line, so the driving and basal stresses dominate. (b) With the Coulomb modification in Eqn (17b) there is a clear transition from power-law drag to Coulomb friction. The basal stress vanishes at the grounding line, and instead the extensional stress divergence becomes enhanced, ultimately balancing the driving stress at the grounding line. We note that the extensional stress is enhanced, but the driving stress also drops significantly compared with the power-law case.
Finally, we note that since the basal stresses in the Coulomb modification drop to zero at the grounding line, the shear stress is continuous across the grounding line. Thus, the stress singularity encountered at the grounding line in many numerical models (e.g. Reference WilchinskyWilchinsky, 2007; Reference Nowicki and WinghamNowicki and Wingham, 2008; Reference Durand, Gagliardini, De Fleurian, Zwinger and Le MeurDurand and others, 2009), which is inherent to the power-law description, may disappear in the Coulomb case. While the Coulomb regime would still need to be resolved for a numerical model to be accurate, the behavior of such a model in the Coulomb regime should be better behaved than in the pure power-law case.
Ice-Sheet Stability with Coulomb Basal Conditions
The numerical solutions discussed in the previous section show that the transition from power-law to Coulomb basal rheology close to the grounding line substantially alters the ice-sheet shape, velocity and stress balance in the boundary layer. In this section, we explore the impact of this change in boundary-layer structure on the stability of the ice sheet.
Following Reference SchoofSchoof (2007a), we use the small dimensionless extensional stress parameter, ε ≪ 1, to perform an asymptotic expansion of the ice-sheet equations (Eqns (16) and (17)). Away from the grounding line, the leading-order balance, corresponding to the limit ε → 0 in Eqn (17a), is simply between the driving and basal stresses. However, close to the grounding line, Eqn (19d) suggests that the extensional stress divergence term should become ![]() , which may be accommodated via the development of a boundary layer. We therefore seek a rescaling of Eqns (16) and (17) to describe the dynamics asymptotically close to the grounding line,
, which may be accommodated via the development of a boundary layer. We therefore seek a rescaling of Eqns (16) and (17) to describe the dynamics asymptotically close to the grounding line,
where α, ζ and γ are the exponents on ε for u, x and h respectively. The expectation, then, is that all of the terms in Eqn (17a) should appear at the same order in ε in the rescaled variables.
As explained above, sufficiently close to the grounding line, the basal sliding should follow a Coulomb rheology rather than a power-law rheology, so we assume that the basal shear stress is described by Eqn (7). First, anticipating that ζ > 0, we note from Eqn (16) that the ice flux, q = hu, should be approximately unchanged over the boundary layer,
so in the limit ε → 0 the ice flux must be equal to the ice flux far from the grounding line, ![]() . (Note that the subscript X in Eqn (21) refers to an X derivative, as before.) Under our scalings of Eqn (20), this is only possible if γ = −α, such that the rescaled ice flux, Q = HU, remains
. (Note that the subscript X in Eqn (21) refers to an X derivative, as before.) Under our scalings of Eqn (20), this is only possible if γ = −α, such that the rescaled ice flux, Q = HU, remains ![]() as ε → 0. This constraint simplifies Eqn (17a), which can be rewritten as
as ε → 0. This constraint simplifies Eqn (17a), which can be rewritten as

where ![]() should be interpreted as
should be interpreted as ![]() , because
, because ![]() is positive and thus UX
is negative. Here the depth of the bed,
is positive and thus UX
is negative. Here the depth of the bed, ![]() , is also assumed to be asymptotically small, which physically implies that the ice grounds in relatively shallow water. This is imposed by the requirement that the mass-conservation equation (Eqn (16)) remain balanced as ε → 0, as discussed above and by Reference SchoofSchoof (2007a). However, the length scale of bathymetry variations is comparable to that of [x] (i.e. the ice-sheet length scale), implying that BX
is
, is also assumed to be asymptotically small, which physically implies that the ice grounds in relatively shallow water. This is imposed by the requirement that the mass-conservation equation (Eqn (16)) remain balanced as ε → 0, as discussed above and by Reference SchoofSchoof (2007a). However, the length scale of bathymetry variations is comparable to that of [x] (i.e. the ice-sheet length scale), implying that BX
is ![]() , rather than
, rather than ![]() like HX
. In other words, the ice-sheet surface changes rapidly close to the grounding line, but the bathymetry does not. To first order in ε, then, the BX
term can be dropped and H
f = B/(1 − δ) can be set constant and equal to the scaled grounding-line thickness, H
g = ε
−γ
h
g. Balancing powers of ε in Eqn (22) we obtain the following exponents,
like HX
. In other words, the ice-sheet surface changes rapidly close to the grounding line, but the bathymetry does not. To first order in ε, then, the BX
term can be dropped and H
f = B/(1 − δ) can be set constant and equal to the scaled grounding-line thickness, H
g = ε
−γ
h
g. Balancing powers of ε in Eqn (22) we obtain the following exponents,
Thus, the ice-sheet thickness becomes asymptotically small relative to the thickness further inland, while the velocity becomes asymptotically large. As discussed above, the resulting scalings in Eqn (20) eliminate the dependence on the bathymetric slope in Eqn (22), resulting in the leading-order force balance,
and ice conservation equation,
where Q is constant across the boundary layer.
This boundary-layer scaling (Eqn (23)) differs from Reference SchoofSchoof (2007a) for a power-law grounding-line basal rheology, who obtained the following exponents

Note that we use an inverse definition of m, i.e. m = 1/m
Schoof, resulting in a different algebraic form in Eqn (26). For n = m = 3, our scaling in Eqn (23) estimates a grounding-line thickness of ![]() , whereas Reference SchoofSchoof’s (2007a) scalings in Eqn (26) yield
, whereas Reference SchoofSchoof’s (2007a) scalings in Eqn (26) yield ![]() . Thus, an immediate prediction of these boundary-layer scalings is that the grounding-line ice thickness should be smaller under a Coulomb basal rheology than under a power-law basal rheology (for sufficiently small ε), which is consistent with the numerical results shown in Figure 3.
. Thus, an immediate prediction of these boundary-layer scalings is that the grounding-line ice thickness should be smaller under a Coulomb basal rheology than under a power-law basal rheology (for sufficiently small ε), which is consistent with the numerical results shown in Figure 3.
In order to make further analytical progress with the boundary-layer force balance (Eqn (24)), we eliminate H using Eqn (25) and define ![]() , again following Reference SchoofSchoof (2007a). This allows us to write Eqn (24) as a pair of ordinary differential equations for U and W,
, again following Reference SchoofSchoof (2007a). This allows us to write Eqn (24) as a pair of ordinary differential equations for U and W,

The flotation and stress continuity conditions at the grounding line, given by Eqns (19c) and (19d), yield the rescaled boundary conditions for U and W,

and, in order to match with the region far from the grounding line, both U and W must vanish as X → ∞:
This matching condition arises in the limit ε → 0, in which the boundary layer becomes infinitesimally thin, and so the rest of the ice sheet approaches infinity in the boundary-layer coordinate, X. The rescaling in Eqn (20) then implies that the velocity outside the boundary layer is infinitesimally small relative to the velocity inside the boundary layer, and hence that U → 0 as X → ∞. It follows that a similar condition on UX , and thus on W, must also hold.
At this point, the boundary-layer problem (Eqns (27–29)) can be solved numerically to yield the results in Figure 5. Specifically, for a given Q, we find that there exists a unique choice of H g that satisfies the second boundary condition at (U, W) = (0, 0), with all other solutions diverging. The blue curve labeled ‘solution’ in Figure 5 is that unique numerical solution that satisfies both the grounding-line boundary conditions of Eqn (28) (at the blue circle) and the outer boundary condition of Eqn (29) as X → ∞. Unlike Schoof’s power-law case, different H g result in different governing equations for Eqn (27), so there is a different phase plane for each choice of H g. We therefore only show the phase plane with the correct choice of H g. For Figure 5, we use Q = 10 for the purposes of illustration, which implies H g = 34:9575. The solution is qualitatively similar for all choices of Q, which is confirmed by the further scaling analysis below. Note that, as with the extensional stress divergence in Figure 4, we observe that the magnitude of the scaled strain rate, W, does not increase monotonically towards the grounding line, but instead reaches a maximum prior to the grounding line and then falls off to a lower value. By substituting Eqn (28) into Eqn (27), one can show that WX > 0 at the grounding line and, hence, that there is always a strain-rate maximum in the boundary layer.
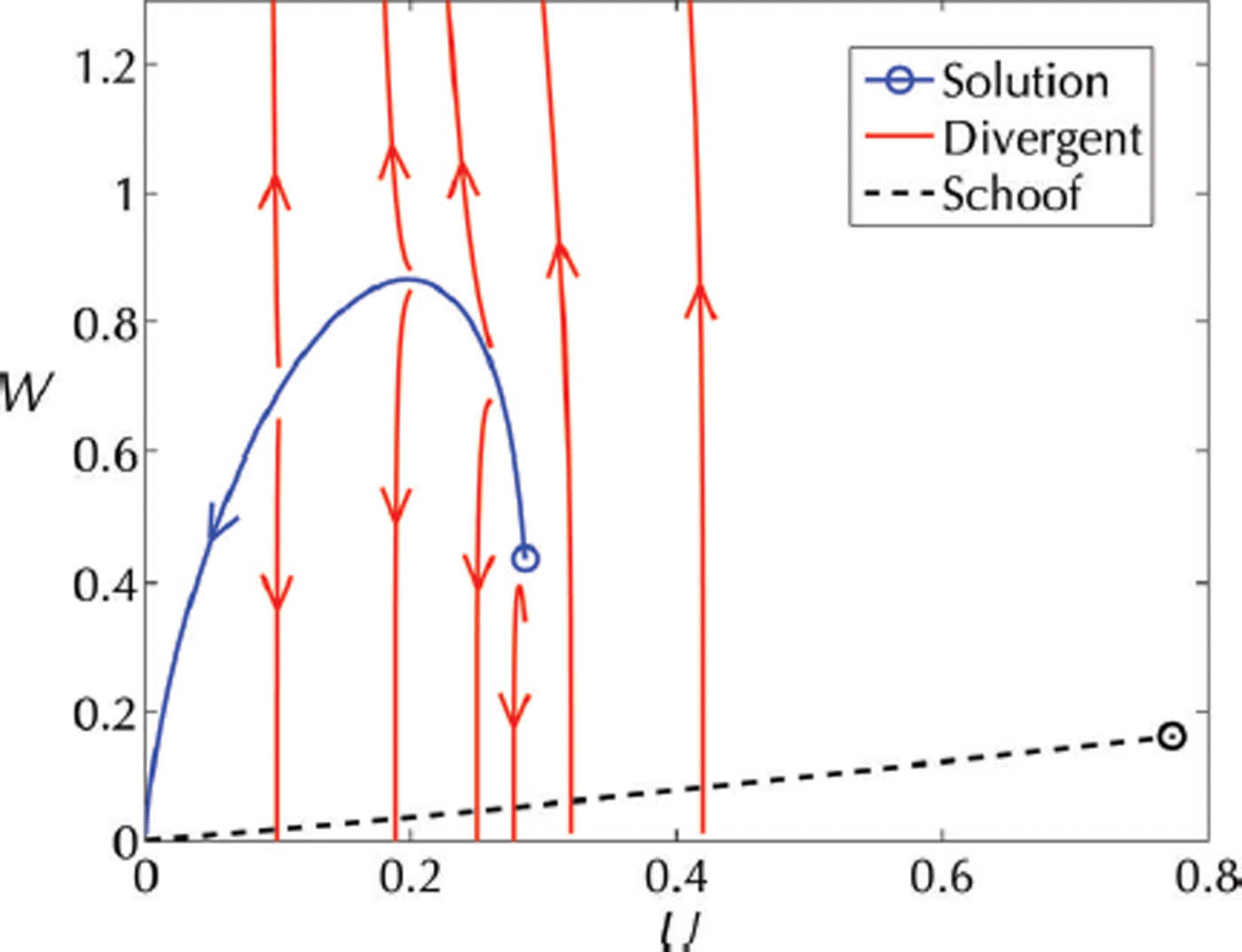
Fig. 5. Boundary-layer phase plane for scaled strain rate, ![]() , vs scaled velocity, U, with Q = 10, n = 3, δ = 0.1. Circles denote the grounding-line position in phase space. The dashed curve shows the result of Reference SchoofSchoof (2007a) for the power-law case, with m = 3, which has a scaling of W ∼ U
10/9, and hence is nearly linear. The blue solid curve shows the result with Coulomb friction, with
, vs scaled velocity, U, with Q = 10, n = 3, δ = 0.1. Circles denote the grounding-line position in phase space. The dashed curve shows the result of Reference SchoofSchoof (2007a) for the power-law case, with m = 3, which has a scaling of W ∼ U
10/9, and hence is nearly linear. The blue solid curve shows the result with Coulomb friction, with ![]() = 500, which has a scaling of W ∼ U
2/n
as (U, W) → (0, 0) to satisfy Eqn (27) as X → ∞. Near the grounding line, W drops so that (unlike in the power-law case) the maximum W is not at the grounding line. The red solid curves denote numerical solutions for the Coulomb case with initial conditions that diverge and therefore do not result in a solution.
= 500, which has a scaling of W ∼ U
2/n
as (U, W) → (0, 0) to satisfy Eqn (27) as X → ∞. Near the grounding line, W drops so that (unlike in the power-law case) the maximum W is not at the grounding line. The red solid curves denote numerical solutions for the Coulomb case with initial conditions that diverge and therefore do not result in a solution.
To determine a relationship between Q and H
g in the Coulomb case, we seek a further rescaling of Eqns (27–29) that removes the dependencies on H
g and ![]() . We find that this is uniquely achieved by setting
. We find that this is uniquely achieved by setting

where variables with tildes are the newly scaled variables. This choice then simplifies Eqns (27–29) to

which are indeed independent of H
g and ![]() . The dependence of Q on other variables is determined by Eqn (30), once Eqns (31–33) are solved to determine the appropriate
. The dependence of Q on other variables is determined by Eqn (30), once Eqns (31–33) are solved to determine the appropriate ![]() for a given δ (which is analogous to determining H
g for a given Q, as done previously). These numerically determined values of
for a given δ (which is analogous to determining H
g for a given Q, as done previously). These numerically determined values of ![]() are plotted in Figure 6 for a range of δ in the n = 3 case. As shown,
are plotted in Figure 6 for a range of δ in the n = 3 case. As shown, ![]() scales nearly as δ
2 and it is shown in the Appendix that
scales nearly as δ
2 and it is shown in the Appendix that ![]() generally scales as (δ/8)
n
−1. Thus, we rewrite the scaling for Q as
generally scales as (δ/8)
n
−1. Thus, we rewrite the scaling for Q as

Fig. 6. Scaled grounding-line ice flux, ![]() , vs δ, for n = 3 and
, vs δ, for n = 3 and ![]() = 500, where
= 500, where ![]() is defined in Eqn (30). The green circles are numerical solutions from solving Eqns (31–33), and the blue curve is the scaling of Eqn (34),
is defined in Eqn (30). The green circles are numerical solutions from solving Eqns (31–33), and the blue curve is the scaling of Eqn (34), ![]() , with Q
0 = 0.61 chosen to match the numerical solution at δ = 0.1. Since
, with Q
0 = 0.61 chosen to match the numerical solution at δ = 0.1. Since ![]() was constructed to be independent of
was constructed to be independent of ![]() , the figure is identical for all choices of
, the figure is identical for all choices of ![]() .
.

where Q
0 is a constant determined by numerically solving Eqns (31–33). For the special case of interest where δ = 0.1 and n = 3, Q
0 = 0.61; furthermore, 0:60 ≤ Q
0 ≤ 0.65 over the entire range of δ plotted in Figure 6. For n = 3, then, the ice flux, Q, in the Coulomb case scales as grounding-line thickness to the fifth power (i.e. ![]() ), and inversely with the scaled friction coefficient. This contrasts with the expression of Reference SchoofSchoof (2007a) (Eqn (6)) for the power-law case which, in scaled variables, can be expressed as
), and inversely with the scaled friction coefficient. This contrasts with the expression of Reference SchoofSchoof (2007a) (Eqn (6)) for the power-law case which, in scaled variables, can be expressed as

We note that our result in Eqn (34) is different to the m → ∞ (m
Schoof = 0) limit of Eqn (35), which has ![]() , and so the Coulomb result has distinctly different behavior to that of the ‘perfectly plastic’ limit of the power-law case. Our scaling of Eqn (34) is also different to the preferred choice of Schoof with n = m = 3, which gives
, and so the Coulomb result has distinctly different behavior to that of the ‘perfectly plastic’ limit of the power-law case. Our scaling of Eqn (34) is also different to the preferred choice of Schoof with n = m = 3, which gives ![]() , as well as different to the scaling of Reference WeertmanWeertman (1974) of
, as well as different to the scaling of Reference WeertmanWeertman (1974) of ![]() . The dependence of ice flux on grounding-line thickness for the Coulomb case is therefore stronger than in either the preferred Reference SchoofSchoof (2007a) or Reference WeertmanWeertman (1974) cases (but not as strong as in the perfectly plastic limit).
. The dependence of ice flux on grounding-line thickness for the Coulomb case is therefore stronger than in either the preferred Reference SchoofSchoof (2007a) or Reference WeertmanWeertman (1974) cases (but not as strong as in the perfectly plastic limit).
This increased sensitivity in turn implies that positive bed slopes (sloping down towards the ocean) are more stable than in the power-law case and negative bed slopes are more unstable. It also explains why the grounding lines in the Coulomb case (e.g. in Fig. 3a) generally lie upstream of the grounding lines in the power-law case, as a stable configuration is reached at a lower value of (positive) bed slope in the Coulomb case (Reference SchoofSchoof, 2012). Both of these conclusions can be understood better by comparing the two scalings for the non-dimensional grounding-line ice flux, ![]() , which may be expressed as
, which may be expressed as

and

for the Coulomb and power-law cases, respectively. One can use Eqns (36) and (37) to compare the sensitivities to perturbations for a given bed slope gradient, ![]() , since
, since ![]() . Substituting our reference parameters into Eqns (36) and (37) yields
. Substituting our reference parameters into Eqns (36) and (37) yields ![]() in the power-law case and
in the power-law case and ![]() in the Coulomb case, verifying that the Coulomb case is indeed more sensitive to bathymetry variations. This result is robust for realistic parameter variations. Additionally, solving for
in the Coulomb case, verifying that the Coulomb case is indeed more sensitive to bathymetry variations. This result is robust for realistic parameter variations. Additionally, solving for ![]() for a given value of
for a given value of ![]() (and n = m = 3) shows that
(and n = m = 3) shows that ![]() scales as ε
3/5 in the Coulomb case and as ε
9/19 in the power-law case, as suggested above, so that in the limit ε → 0,
scales as ε
3/5 in the Coulomb case and as ε
9/19 in the power-law case, as suggested above, so that in the limit ε → 0, ![]() will be smaller in the Coulomb case for the same grounding-line flux. For example, fixing
will be smaller in the Coulomb case for the same grounding-line flux. For example, fixing ![]() and using the reference values of parameters as earlier, we find
and using the reference values of parameters as earlier, we find ![]() in the Coulomb case and
in the Coulomb case and ![]() in the power-law case. Thus, the ice sheet should indeed ground in shallower water under Coulomb basal conditions, consistent with the numerical solution shown in Figure 3a. A shallower grounding is a robust result for realistic variations of the model parameters; an order-of-magnitude increase in ε would be required to produce a deeper grounding line in the Coulomb friction case than in the power-law case. Given that the ice sheet can only ground stably on positive bed slopes, this means that Coulomb friction typically produces a grounding line that lies upstream, closer to any negative bed slopes further inland.
in the power-law case. Thus, the ice sheet should indeed ground in shallower water under Coulomb basal conditions, consistent with the numerical solution shown in Figure 3a. A shallower grounding is a robust result for realistic variations of the model parameters; an order-of-magnitude increase in ε would be required to produce a deeper grounding line in the Coulomb friction case than in the power-law case. Given that the ice sheet can only ground stably on positive bed slopes, this means that Coulomb friction typically produces a grounding line that lies upstream, closer to any negative bed slopes further inland.
As shown in Figure 7, there is also excellent agreement between the grounding-line position predicted from the boundary-layer theory result of Eqn (34) and the numerical results over a wide range of ε. This agreement demonstrates that the boundary-layer theory can be used to accurately predict the location of the grounding line.

Fig. 7. Scaled grounding-line position, x g, vs ε. The red solid curve is from numerically solving Eqns (16–19), as described for Figure 3. The black dashed curve is predicted using the boundary-layer scaling by solving for the position at which the flux determined by integrating accumulation matches the theoretical ice flux of Eqn (29).
Finally, we note that the scaling of Eqn (34) can be substituted back to determine the dimensionally correct grounding-line ice flux in the Coulomb case to be

where Q 0 ≈ 0:61 is a numerical coefficient determined by the boundary-layer analysis.
A Posteriori Simplified Derivations of Ice-Sheet Stability
The boundary-layer analysis of the previous section provides a rigorous analysis of the force balance near the grounding line. The results, however, provide a basis for presenting a simplified analysis of the key balances at the grounding line. Specifically, we find that neglecting the boundary layer altogether leads to similar scalings for the ice flux at the grounding line. We first present this approximation for the power-law case and then describe the Coulomb analog. In the power-law case, we neglect the extensional stress term throughout the boundary layer, although we include this term to satisfy the grounding-line condition given in Eqn (5b). As discussed above, the apparent contradiction here is due to the fact that the divergence of the extensional stress remains small compared with the other stresses at the grounding line (see Fig. 4a). We also justify this approach based on the recovery of results from the full boundary-layer analysis.
After neglecting the extensional stress term in Eqn (2) and applying the power-law basal stress law, Eqn (1), we further assume that hx ≫ bx within the boundary layer. This approximation, which is in agreement with our numerical solutions, leads to
The additional constraints include continuity of stress across the grounding line (Eqn (5b)), which simplifies to

and mass conservation

This simplified set of equations (Eqns (39–41)) is a closed system that determines the ice-sheet profile, ice flux and position of the grounding line. Combining the three yields
This relationship can then be used to solve for the ice flux at the grounding line, ![]() , which exactly reproduces the relationship given in Eqn (6). Again, the insight here is that even in the boundary layer, the extensional stress divergence makes a relatively small contribution to the force balance, as shown schematically in Figure 1 and numerically in Figure 4a. This result follows from the boundary-layer analysis of Reference SchoofSchoof (2007a), since the limit of small H
f requires a balance between driving stress and power-law basal stress at the grounding line.
, which exactly reproduces the relationship given in Eqn (6). Again, the insight here is that even in the boundary layer, the extensional stress divergence makes a relatively small contribution to the force balance, as shown schematically in Figure 1 and numerically in Figure 4a. This result follows from the boundary-layer analysis of Reference SchoofSchoof (2007a), since the limit of small H
f requires a balance between driving stress and power-law basal stress at the grounding line.
A similar analysis can be carried out for the Coulomb case, but the assumptions necessary cannot be rigorously justified, as in the power-law case. Introducing Coulomb friction to the left-hand side of Eqn (39) and again neglecting horizontal gradients in the bed profile gives
This balance is valid at the upstream edge of the Coulomb boundary layer where, additionally, h ≫ h f (for a thin grounding line), resulting in hx = −f. Although the extensional stress divergence cannot be neglected over the boundary layer in this case, it is still expected to be relatively small. This suggests that hx ∼ −f is a reasonable scaling near the grounding line as well. However, at the grounding line itself, the Coulomb case requires zero basal stress, so that driving stress is balanced by the extensional stress term, which in turn is locally set by the stress boundary condition of Eqn (19d). This suggests that hx scales with δ near the grounding line, but retains the same dependence on f. Thus, the profile ‘tapers off’ by a factor of δ as it approaches the grounding line, i.e. hx ∼ −δf. We therefore postulate that hx ≈ −δf is a reasonable guess for the slope dependence at the grounding line (within the boundary layer). While this assumption is not rigorously justified, the choice is shown to reproduce the boundary-layer scaling. The result is presented as additional intuition for how the flux scales with different parameters (e.g. h f) but should not be viewed as a way to bypass the full boundary-layer analysis.
Substituting the conditions for stress across the grounding line (Eqn (40)) and mass conservation (Eqn (41)) we have
which results in the relationship for ice flux at the grounding line as a function of grounding-line thickness,
which is identical to the exact boundary-layer theory result of Eqn (38), except without the ![]() factor of 8Q
0 ≈ 4.9.
factor of 8Q
0 ≈ 4.9.
The full boundary-layer analysis offers insight into the principal balances near the grounding line. The simplified analysis presented here provides a more intuitive understanding of how the scaling differs between the power-law and Coulomb cases.
Conclusions
In this work, we have presented a one-horizontal-dimension model of ice-sheet dynamics in which the basal stresses near the grounding line are governed by Coulomb friction rather than the more commonly assumed power-law basal rheology. This transition in stress regime is a consequence of the flotation condition at the grounding line, and results in a somewhat narrow ‘Coulomb’ region near the grounding line, where the ice sheet has distinctly different properties to those it would have had without Coulomb friction. Specifically, the ice sheet grounds at a substantially different location, ice-sheet surface profiles take on a distinctly different shape, with a tapering off nearly exponentially towards the grounding line, and the basal stresses reduce to zero at the grounding line, potentially removing the stress singularity inherent to a power-law rheology. Unlike the standard power-law case, this implies that the largest extensional stress terms are not at the grounding line, but instead reach a maximum prior to reaching the grounding line and subsequently diminish in magnitude. These differences in the predicted surface profiles and stresses could be verified with high-resolution data near the grounding line.
Despite the general narrowness of the region where Coulomb basal friction dominates over the power-law behavior, including Coulomb friction nonetheless results in substantially different conclusions for ice-sheet stability. In particular, we find that the inclusion of Coulomb friction results in a boundary layer at the grounding line that has a distinctly different scaling of ice flux with grounding-line thickness (![]() for n = 3), compared with the power-law case (
for n = 3), compared with the power-law case (![]() for n = m = 3). The stronger dependence of ice flux on grounding-line thickness in turn causes positive bed slopes (sloping down towards the ocean) to be more stable and negative bed slopes (sloping down towards the interior of the ice sheet) to be more unstable to climate perturbations. Furthermore, with Coulomb friction, the ice sheet grounds in shallower water, placing the grounding line closer to highly unstable regions of negative bed slope. Thus, ice sheets are generally more sensitive to perturbations than previously recognized. With the large number of recent observations of parts of the Antarctic ice sheet with negative or near-negative bed slopes (e.g. Reference FavierFavier and others, 2014; Reference Joughin, Smith and MedleyJoughin and others, 2014; Reference Mengel and LevermannMengel and Levermann, 2014; Reference Rignot, Mouginot, Morlighem, Seroussi and ScheuchlRignot and others, 2014), our stability results may have important implications for the future of the Antarctic ice sheet.
for n = m = 3). The stronger dependence of ice flux on grounding-line thickness in turn causes positive bed slopes (sloping down towards the ocean) to be more stable and negative bed slopes (sloping down towards the interior of the ice sheet) to be more unstable to climate perturbations. Furthermore, with Coulomb friction, the ice sheet grounds in shallower water, placing the grounding line closer to highly unstable regions of negative bed slope. Thus, ice sheets are generally more sensitive to perturbations than previously recognized. With the large number of recent observations of parts of the Antarctic ice sheet with negative or near-negative bed slopes (e.g. Reference FavierFavier and others, 2014; Reference Joughin, Smith and MedleyJoughin and others, 2014; Reference Mengel and LevermannMengel and Levermann, 2014; Reference Rignot, Mouginot, Morlighem, Seroussi and ScheuchlRignot and others, 2014), our stability results may have important implications for the future of the Antarctic ice sheet.
Acknowledgements
We thank G.H. Gudmundsson for useful discussions, and two anonymous reviewers for helpful suggestions. This research was carried out at the Jet Propulsion Laboratory and the California Institute of Technology under a contract with the National Aeronautics and Space Administration and funded through the President’s and Director’s Fund Program. Partial support was also provided by the Stanback Discovery Fund for Global Environmental Science.
Appendix
To determine how Q scales with δ, we start with Eqns (31– 33) and first observe that δ ≪ 1 implies that ![]() , so
, so ![]() is approximately constant within the boundary layer, to order δ. Yet the UX
term must become
is approximately constant within the boundary layer, to order δ. Yet the UX
term must become ![]() at the grounding line in a boundary-layer theory with δ as the parameter that approaches zero, so we seek a further rescaling for the boundary-layer equations. Introducing Δ ≡ δ/8, we then introduce a new scaling of variables with Δ as
at the grounding line in a boundary-layer theory with δ as the parameter that approaches zero, so we seek a further rescaling for the boundary-layer equations. Introducing Δ ≡ δ/8, we then introduce a new scaling of variables with Δ as

which results in

if r
1 and r
2 are chosen as r
1 = 0, r
2 = n − 1. This choice ensures that the terms in Eqn (A2) balance at leading order in Δ. We note that the far-field condition analogous to Eqn (33) can be satisfied by an appropriate choice of ![]() . This analysis therefore suggests that
. This analysis therefore suggests that
![]() , where
, where ![]() is an
is an ![]() quantity that is independent of δ as δ → 0. As shown in Figure 6, this scaling is numerically verified in the case where n = 3.
quantity that is independent of δ as δ → 0. As shown in Figure 6, this scaling is numerically verified in the case where n = 3.









