Introduction
During the last several decades, the kinematics of ice glaciers has been studied intensively. This work has involved formulation of a flow law for glacier ice, assessment of strain patterns on glaciers, and development of an understanding of relationships between these patterns and dynamic controls related to glacier mass balance and geometry (Reference PatersonPaterson, 1994). In recent years, understanding of rock glacier kinematics has also progressed, as a result of borehole, laboratory and surface studies, particularly in the Alps, but it continues to lag behind our knowledge of ice glaciers. We currently lack a clear understanding of the constitutive relationship for rock glacier material. Understanding of patterns of surface strain in rock glaciers and explanation of these patterns in terms of mass balance, geometry, surface morphology and flow characteristics is also incomplete. Our less developed understanding of rock glacier deformation reflects several factors. Because they are complexly structured mixes of ice and rock, it is to be expected that rock glaciers will have complex and diverse flow characteristics. Additionally, there are many impediments to detailed study of rock glacier deformation, including difficulties of coring, of conducting laboratory experiments on heterogeneous ice–debris mixtures, and of making accurate and representative measurements of small differential movements of typically unstable surface materials.
In this paper, we present data from a 14 year (1985–99) survey of surface strain and its relationship to rock glacier morphology at Spruce Creek rock glacier, in the Ten Mile Range of the Colorado Rockies, USA. The work was conducted as part of a broader project on rock glacier flow, which also examined flow velocities over interannual to millennial time-scales. We utilized simple but precise steel-tape measurements to assess strain.
Previous Work on Rock Glacier Kinematics
Since the pioneering work of Reference Wahrhaftig and CoxWahrhaftig and Cox (1959), many workers have examined rock glacier surface flow velocities, using field-survey (e.g. Reference WhiteWhite, 1971; Reference PotterPotter, 1972; Reference Benedict, Benedict and SanvilleBenedict and others, 1986; Reference Konrad, Humphrey, Steig, Clark, Potter and PfefferKonrad and others, 1999), photogrammetric (e.g. Reference Messerli and ZurbuchenMesserli and Zurbuchen, 1968; Reference Barsch and HellBarsch and Hell, 1975; Reference Haeberli, King and FlotronHaeberli and others, 1979; Reference Kääb, Haeberli and GudmundssonKääb and others, 1997, Reference Kääb, Gudmundsson, Hoelzle and Allard1998, Reference Kääb, Isaksen, Eiken and Farbrot2002; Reference Frauenfelder and Kääb.Frauenfelder and Kääb, 2000; Reference Kaufmann, Ladstadter, Springman and ArensonKaufmann and Ladstädter, 2003) or synthetic aperture radar (SAR) methods (Reference Rignot, Hallet and FountainRignot and others, 2002; Reference Kenyi, Kaufmann, Springman and ArensonKenyi and Kaufmann, 2003). Subsurface deformation has been examined in several borehole studies (Reference Johnson and NicklingJohnson and Nickling, 1979; Reference WagnerWagner, 1992; Reference Hoelzle, Wagner, Kääb, Vonder Mühll. and AllardHoelzle and others, 1998; Reference Arenson, Hoelzle and SpringmanArenson and others, 2002, Reference Arenson, Springman, Hawkins, Phillips, Springman and Arenson2003a), and rock glacier material has been deformed experimentally in the laboratory (Reference Arenson, Almasi, Springman, Springman and ArensonArenson and others, 2003b). A few studies have examined surface strain in detail, assessing strain either related to particular surface features by making repeated steel-tape measurements (Reference PotterPotter, 1972; Reference White, Giardino, Shroder and VitekWhite, 1987) or by photogrammetry. Reference Haeberli, King and FlotronHaeberli and others (1979) used photogrammetry to assess strain rates at Gruben rock glacier, Swiss Alps, and Kääb and his coworkers (Reference Kääb, Haeberli and GudmundssonKääb and others, 1997, Reference Kääb, Gudmundsson, Hoelzle and Allard1998; Reference Kääb and VollmerKääb and Vollmer, 2000) continued and refined this approach, using high-precision photogrammetry to determine principal strain axis orientations and strain rates at several Swiss rock glaciers.
Field Area
Spruce Creek rock glacier is located on the eastern flank of the Ten Mile Range of Colorado (Fig. 1). It is fed by rockfall from the back- and side-walls of the northeast cirque of 4252m Pacific Peak (Fig. 2). The back wall rises steeply 250 m from talus at the head of the rock glacier to the peak. Bedrock is almost exclusively Proterozoic high-grade meta-morphic rock, primarily biotitic gneiss (Reference TwetoTweto, 1974), with pegmatite and other dike rocks present in low abundance. Rock glacier surface material is overwhelmingly coarse, angular gneiss. Clasts several meters in diameter are common. The rock glacier surface is generally nonvegetated, except for sparse lichen cover.

Fig. 1. Location map. Heavy lines are drainage divides; light lines are streams. Insert maps shows the state of Colorado. Lines on insert map are crests of mountain ranges.

Fig. 2. Spruce Creek rock glacier. Dashed lines indicate the down-valley extents of two lobes impinging on the lower portion of the rock glacier. Dotted line indicates the position of the pronounced longitudinal furrow in the lower portion of the rock glacier. Photograph by US Department of Agriculture Forest Service, taken on 3 October 1972.
No meteorological data are available for the Spruce Creek valley. The nearest station with continuous records is Climax, Colorado (Western Regional Climate Center, http://www.wrcc.dri.edu/cgi-bin/cliMAIN.pl?coclim), 8–9km to the southwest at 3460 m a.s.l. Combining data from this station with regional annual and summer lapse rates of approximately 0.62ºC(100mΓ 1 and 0.73ºC(100mΓ 1 respectively (Leonard, unpublished information) indicates annual and July mean temperatures at the rock glacier of about –4ºC and 7ºC respectively. No data are available on ground temperatures at the rock glacier.
Rock Glacier Morphology
The rock glacier extends about 700 m down-valley, from its head in steep talus and semi-permanent snowfields at ~4000ma.s.l., to a terminus at ~3870ma.s.l. Its width ranges from about 200 m in its upper portion to 280 m near the terminus. Surface slope of the uppermost 150 m of the rock glacier, where it grades into talus, averages about 15º. The slope of the lower 550 m of the rock glacier averages 5.9º, but varies along two gentle rolls evident in a center-line longitudinal profile (Fig. 3). At the terminus, there is a sharp break between the top and frontal slopes. The 40–45 m high frontal slope ranges from 40º to 46º, excluding a basal talus apron, closely comparable to slopes on active rock glacier fronts in the Colorado Front Range (Reference WhiteWhite, 1971).

Fig. 3. Center-line longitudinal profile of the lower 550 m of Spruce Creek rock glacier. Solid arrows indicate the position of surveyed cross-rock-glacier velocity transects; open arrows indicate major morphological features of the rock glacier surface. Letters show the approximate positions of strain diamonds projected to the center line, and dashed lines and angles indicate changes in surface slope of the rock glacier. Profile was produced photogrammetrically.
Surface morphology of the rock glacier suggests that its upper portion consists of two lobes that are impinging upon the lower portion (Figs 2 and 3). The down-glacier margin of each lobe is a steep, 3–6m high, down-glacier-facing scarp that is convex down-glacier. A sharp gradient in lichen size occurs across each scarp, suggesting abrupt down-glacier increases in surface age or stability (Leonard and others, unpublished information). As will be discussed below, measured flow velocities are higher up-glacier from the scarps than down-glacier, further supporting the suggestion that more active, up-glacier lobes are impinging upon less active material down-glacier.
Ridge and furrow topography is well developed on some parts of the rock glacier. Transverse ridges are best developed where the upper portion of the rock glacier impinges on the lower. Longitudinal ridges are developed along both sides of the rock glacier, particularly the southern (right) margin. A well-developed longitudinal furrow bisects the lower portion of the rock glacier (Fig. 2). Patterns of transverse ridges are not continuous across this furrow, and there is some indication in velocity measurements that the two sides of the rock glacier may move somewhat independently of one another across the furrow (Leonard, unpublished information).
Many aspects of the morphology of the rock glacier, particularly its steep frontal slope, surface and frontal instability and lack of vegetation cover, suggest that it is active at present. As is discussed below, however, measured flow velocities and strain rates are quite low.
Study Aims
The principal aims of this study were to assess patterns and variations in surface strain on Spruce Creek rock glacier and to relate these patterns to the rock glacier morphology. We hoped to document the relationship of surface strain to position on rock glacier, changes in slope, transverse ridges and impinging up-glacier lobes.
Methodology
Measured strain rates at Spruce Creek rock glacier (discussed below) are typically on the order of 10–4a–1. To examine strain patterns related to rock glacier morphology, it was necessary to measure differential movements over distances of no more than a few tens of meters. Thus, we needed to measure accurately differential movements of only a few mm a–1. Even if strain were measured over several-year time intervals, cm-scale accuracy was necessary. Of the two methods previously utilized in strain analysis of rock glaciers, only steel-tape measurements are capable of cm- scale accuracy (Reference White, Giardino, Shroder and VitekWhite, 1987). Photogrammetric methods are capable of only decimeter-scale accuracy (Reference Kääb, Haeberli and GudmundssonKääb and others, 1997), too coarse to document strain over short distances on a very slowly deforming feature. In recent years, development of total station survey instruments and SAR has made available additional means of assessing differential movement at cm-scale accuracy, possibly mm scale under optimal conditions with SAR (Reference Rignot, Hallet and FountainRignot and others, 2002). These methods were not available at the time of initiation of this study, and while future studies of low-strain-rate rock glaciers will undoubtedly make use of these methods, they do not yet offer data of the time depth of the current steel-tape study.
Field methods
Reference NyeNye (1959) proposed using steel-tape measurements to evaluate strain on ice glaciers and we used a modified version of his method. Nye’s method involved placing five stakes in the ice, four in a square, or ‘strain-diamond’, pattern with the diagonals of the diamond parallel and perpendicular to ice-flow direction. The fifth stake was located in the center of the diamond. Repeat steel-tape distance measurements between the stakes provided eight independent measures of linear strain from which the strain tensor was calculated. In theory, the tensor could be calculated from three non-parallel measurements, but this would yield reliable results only if strain were homogeneous over the area measured. The five additional measurements allowed Nye to average data to reduce the effect of nonhomogeneity. In this study, marked boulders were used in the place of Nye’s stakes. Unevenness of the rock glacier surface and the necessity of having clear lines of sight between the marked boulders in each diamond made it very difficult to arrange the diamonds with the ideal configuration outlined by Nye. Because the layout of many of the diamonds differed markedly from the ideal geometry, we needed to develop an alternative method of solving for principal strain orientations and magnitudes, and for establishing confidence intervals for these solutions, to that used by Nye. Our method is discussed below.
Strain diamonds were established at 12 sites on the rock glacier (Fig. 4). Nine diamonds (A, B, C, D, E, F, G, H, J) were located along three surveyed velocity transects to allow comparison of strain and velocity data. In addition, three diamonds (I, K and L) were sited to provide fuller coverage of the rock glacier surface. Two diamonds (D and K) were in locations of well-developed transverse ridges and a third (E) in an area of moderately developed ridges.

Fig. 4. Location of strain diamonds and velocity transects. Strain diamonds are indicated with idealized geometry but accurate center position.
At all but one location, five boulders were chosen that most closely approximated the geometry specified by Nye (1959). As there was no suitable boulder in the center of diamond G, only the four corner points were marked. Sides of the diamonds were approximately 25 m long, but varied considerably. Each boulder was marked at a high point with a 5 mm diameter circle of black paint, within a larger circle of brightly colored paint. Distances between marked boulders were measured to the nearest 0.01 ft (~3 mm) with a Lufkin steel tape during windless or very low-wind intervals. Initial measurements were made in September 1985, with subsequent remeasurements in late boreal summer or early fall of 1987, 1989, 1992, 1996 and 1999. Line-length measurements were converted to strain magnitudes by dividing the change in line length by the original length of a line, and to strain rates, expressed in units of a–1, by dividing by the time interval between measurements.
There are several potential sources of error in our method; some related to the measurements themselves, others to the assumption that the measurements are indicators of strain across each diamond. Potential measurement errors include (1) imprecision of steel-tape readings, (2) error in locating the center of the 5 mm black mark at each survey point, (3) error due to application of unequal tension on the steel tape, (4) error due to the effect of wind on measurements, and (5) error due to thermal expansion of the tape. Error related to imprecision of steel-tape readings is approximately ±1.5 mm, and that due to locating the center of the mark is probably about the same. Even with different people applying tension to the tape under different (still-to-gentle) wind conditions, measurements were almost always replicable within 0.02ft (~6mm), similar to the replicability of 5 mm reported by Reference White, Giardino, Shroder and VitekWhite (1987). Thermal expansion of the tape over a 15–20°C temperature range is about 6 mm for the longest measurements. Pooling these independent terms, measurement error should be <1 cm.
Use of these measurements as indicators of strain across a diamond introduces additional sources of error. Our basic assumptions are that, over the scale of individual diamonds, the rock glacier deforms homogeneously and that movement of individual clasts is translational and reflects this overall strain field. Each of these assumptions may be incorrect. Strain may be heterogeneous across diamonds, and individual marked clasts may tilt, rotate or slide with respect to the material below. It may be difficult to separate the effects of broadly non-homogeneous strain across a diamond from such movement of individual clasts. To address these uncertainties, we developed a statistical approach that allows us to find best-fit principal strain axis orientations and magnitudes and to assess confidence intervals around those solutions.
Down-valley movement measurements were made along three bedrock-to-bedrock cross-glacier transects at 2–5 year intervals from 1985 to 2000. Each transect consisted of 8–10 marked clasts on the rock glacier surface. Measurements were made initially using an optical transit and subsequently using a total station.
Mathematical methods
Our statistical approach to assessing strain is based on the fact that a two-dimensional strain tensor for homogeneous strain can be described as an ellipse, with lengths and orientations of the semi-major and semi-minor axes corresponding to the magnitudes and orientations of maximum and minimum principal strains. For homogeneous strain, the magnitudes and orientations of strains in directions other than principal axis directions will also fall on the ellipse. Because surface strain at the rock glacier is almost certainly non-homogeneous, actual strains will deviate from this ideal relationship. Our approach is to find ellipses that best fit the measured strains at each diamond and to calculate confidence intervals for the orientation and magnitude of the ellipse axes.
An ellipse can be written in polar coordinates as

where θ0 is the angle the major axis makes with the positive x axis, and A and B are the semi-major and semi-minor axes respectively. The angle θ0 will be reported between 0° and 180°. Rotating the ellipse by 90° (shifting θ0 by 90° in either direction) will switch the major and minor axes. In the current work, we select θ0 such that A corresponds to the major axis and B to the minor axis.
The best-fit ellipse to the data {Ri, θ i} can be found by minimizing the sum of squares total,
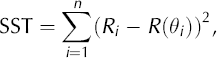
where R(θi) is found using Equation (1). SST is the sum of the squares of the radial distance between the datum and the ellipse. The goal is to find the minimum (specifically the absolute or global minimum) of Equation (2). However, since the global minimum is difficult to find for many functions, we seek a local minimum that occurs when
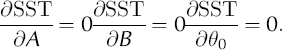
Newton’s method (Reference Burden and FairesBurden and Faires, 2001) is used to solve Equation (3). This technique takes an initial point and, using an iterative formula, converges to a solution to Equation (3). Since a global minimum of Equation (2) is sought, we use 100 random initial points, iterate Newton’s method to solve Equation (3), and select the solution among these that produces the smallest value of Equation (2). Although this does not guarantee a global minimum of Equation (2), in this investigation it does produce the desired result. The values of A, B and θ0 that produce this solution are the best-fit estimators and are denoted A, β and θ0. A standard measure of fit of data to a given curve is r2, the regression coefficient. The model sum of squares (SSM) is
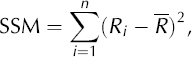
where R is the mean of the radii. Using the two sums of squares listed above, the regression coefficient for the ellipse is
The calculation of many statistical inferences of A, β and θ0 can be found using a bootstrapping method (Reference GoodGood, 1999). This technique is used instead of standard confidence interval calculations because in the latter an assumption is made concerning the underlying distribution of the data. In this analysis, we make no assumption about character of strain and consequently can make no assumption about the underlying distribution of data. Instead, the actual data are used and are randomly resampled to produce a large number of additional datasets. The desired statistical measure is then calculated from these sets. Below we describe the procedure used in this case to calculate the confidence intervals and hypothesis tests for A, B and θ0.
Starting with a set of data (R i, θi) we generate a large set of additional data using the following Monte Carlo procedure:
-
1. The best-fit parameters
 and θ0 are found using the procedure above.
and θ0 are found using the procedure above. -
2. The residuals, εi = Ri – R(θi ) are calculated for each i in the set. The best-fit estimates are used in the calculation of R(θi) using Equation (1).
-
3. A new set of data is created using

 where j is chosen randomly from 1 to n, the size of the dataset.
where j is chosen randomly from 1 to n, the size of the dataset. -
4. The best-fit parameters for the ellipse are found for the dataset
 Again, we use the procedure discussed above.
Again, we use the procedure discussed above. -
5. Steps 3 and 4 are repeated ktimes (we use k = 2000), to generate a distribution of possible values of
 and
and  This procedure is executed for each of the 12 strain diamonds. For each diamond, the procedure yields 2000 values for A, B and θ0. The 95% confidence interval is found by taking the 50th and 1950th points in a ranked list of these values.
This procedure is executed for each of the 12 strain diamonds. For each diamond, the procedure yields 2000 values for A, B and θ0. The 95% confidence interval is found by taking the 50th and 1950th points in a ranked list of these values.
Results
Strain was measured along 93 lines in the 12 diamonds. Measured strain rates were highly variable from line to line and over different time intervals along individual lines. Spatially and temporally averaged measured strain rates for the rock glacier are summarized in Table 1. Averaged over the 14 year period of record, measured strain rates ranged by two orders of magnitude, from 1.0 × 10–5a–1 on the most slowly deforming line to nearly 1.5 × 10–3a–1 on the most rapidly deforming line. Minimum measured strain rates were smaller than the uncertainty of about 4 × 10–5a–1 due to potential measurement error. The rock-glacier-wide mean measured strain rate was (2.8 ± 0.3) × 10–4a–1 (± two standard errors). Measured strain rates (both mean and maximum) decreased by about 20% between the first 7 years of the survey and the last 7 years.
Table 1. Measured strain rates at Spruce Creek rock glacier, 1985–99

Best-fit ellipse calculations were made for each strain diamond based on the entire period of survey. Measured differential movement during individual 2–4 year measurement intervals averaged only 1–2 cm, not much greater than the measurement error. When the entire record was used, however, measured differential movement was typically 5– 10 times the error. Results of the best-fit ellipse calculations are shown in Figure 5, which plots strain rate along measured lines as a function of line orientation for each diamond, and shows the calculated best-fit relationships. Table 2 summarizes results of these calculations and the character and rate of longitudinal (flow-parallel) strain.

Fig. 5. Plots of orientation and strain rate for all measured lines in all strain diamonds. The curve plotted for each diamond is the statistical best-fit ellipse (see text). The r2 value for the fit is given in each plot. The small arrow at the bottom of each plot shows the approximate down-flow direction at that diamond.
Table 2. Calculated principal strain axis orientation and magnitudes. Numbers in parentheses are 95% certainty ranges

For six diamonds (A, B, E, F, G, J) the calculations yielded a close fit to measured data (r2 ≥ 0.790), for three (D, I, K) there was a moderately good fit (0.470 < r2 < 0.560), and for the remaining three (C, H, L) the fit was poor (r2 < 0.240). In the first group, uncertainty in orientation of calculated principal strain axes is generally less than 10°, in the second group it is about ±20° and in the final group it is ±50° or more. The poorness of fit in the latter group could reflect either inhomogeneity of strain across these diamonds, or tilting or sliding of one or more of the marked clasts at a diamond. While the poor fit at these diamonds precludes the use of these best-fit ellipse result for assessing the orientation of principal strain axes and the strain rate along these axes, data from the diamonds are of some use, indicating, for example, that at diamond L, shortening is occurring in all directions, including the flow direction.
Strain parameters are plotted by diamond location in Figure 6. Figure 6a shows the calculated orientations of principal strain axes and their sense of strain (extension or shortening). Lengths of the arrows indicate the relative rates of strain along the principal axes within, but not between, individual diamonds. Strain axes from the three diamonds that yielded poor strain ellipse fits are not plotted. At a first glance, the pattern of principal strain orientations in Figure 6a is complex and it is difficult to deduce an overall pattern. The high r 2 values for the nine diamonds plotted indicate that this complexity is not an artifact of nonhomogeneous strain, or tilting or sliding of measured clasts, but reflects variations in local strain field across the rock glacier. Much, but not all, of the variation is explicable in terms of patterns of longitudinal strain and shearing along the margins of the rock glacier as discussed below. Figure 6b shows the character of longitudinal strain in the flow direction (‘extending flow’ or ‘compressing flow’) at each diamond. Lower-case letters indicate <95% certainty on the character of the longitudinal flow regime at a diamond. A clear pattern of longitudinal strain is evident, with an alternation of compressing and extending flow regimes down-glacier. Figure 6c and d show the maximum measured strain rate and the maximum strain rate determined from the best-fit ellipse calculations respectively for each diamond, both in units of 10–4a–1. The three diamonds yielding poor fits are not plotted in Figure 6d. In both figures, maximum strain rates occur at diamond J, along the north side of the rock glacier, and strain rates are higher in the upper portion of the rock glacier than in the lower portion. Figure 6e shows the per cent change in measured strain rates between 1985–92 and 1992–99. Although strain rates decreased by about 20% overall (Table 1), with rates decreasing by up to 57% at individual diamonds, along the southern margin of the rock glacier strain rates increased by 9–18%.

Fig. 6. Measured and calculated strain parameters including (a) calculated principal strain axis orientations and relative strain rates along the principal axes; (b) calculated longitudinal flow regime, extending (E) or compressing (C), with lower-case letters indicating certainties of <95% in flow regime determination; (c) maximum measured strain rate (×10–4a–1); (d) maximum calculated strain rate (×10–4a–1); (e) per cent change in strain rate between the first 7 years (1985–92) and the second 7 years (1992–99) of the study; and (f) measured mean velocities (1985–2000) along three transect lines.
Down-valley movement profiles along the three surveyed transects are shown in Figure 6f, and calculated down-glacier velocities for the three lines are given in Table 3. Over the 15 year survey interval (AD 1985–2000) down-glacier flow averaged only 4–7 cm a–1 along the three lines, with somewhat higher rates (6–10 cm a–1) near the center line. These rates are near the lower end of the range of rates reported elsewhere for active rock glaciers (Reference Vitek, Giardino, Shroder and VitekVitek and Giardino, 1987; Reference BarschBarsch, 1996; Reference Frauenfelder, Haeberli, Hoelzle, Phillips, Springman and ArensonFrauenfelder and others, 2003). Measured velocities on the upper portion of the rock glacier are 25–50% higher than those on the lower portion, and a reduction of about 2 cm a–1 takes place down-glacier. The difference in flow rate between the upper and lower portion of the rock glacier appears to have decreased through the survey period, due mainly to a slowing of the upper portion of the rock glacier.
Table 3. Down-valley velocities across three surveyed transects

Discussion
Patterns of strain
The principal strain orientations (Fig. 6a) and the resultant character of longitudinal strain (Fig. 6b) yield information on the first-order controls on rock glacier surface strain. The overall pattern of longitudinal strain indicates a strong control by changes in surface slope, with down-valley steepening resulting in extending flow, and down-valley reduction in slope resulting in compressing flow. Gentle rolls in the surface profile of the rock glacier (Fig. 3) are reflected in changes in longitudinal strain. Flow is compressing in the upper portion of the rock glacier (diamond I) where steep talus above gives way to the much flatter rock glacier surface, and then becomes extending somewhat further down-glacier (diamonds G, H and J) where gradient increases again. The central portion of the rock glacier is a broad zone of compressing flow. This compression is related to another shallowing of the surface slope, particularly near diamonds D–F. Near the terminus, where surface gradient again increases, another region of extending flow (diamonds A–C) is evident. Reference Kääb, Gudmundsson, Hoelzle and AllardKääb and others (1998) previously noted a strong control on rock glacier flow regime exerted by changes in surface slope. Compressing flow at diamonds K and L appears to be related less to a change in slope than to the presence of an impinging up-glacier lobe (Fig. 3). While there is no significant slope change near these two diamonds, they are located near the lower end of the upper of two apparent faster-moving lobes that are impinging on the lower portion of the rock glacier. This situation appears to have generated compressional conditions in the frontal portion of the lobes.
Shear strain reflecting low flow velocities along the sides of the rock glacier modifies the overall strain pattern driven by alternations of longitudinal extension and shortening (Fig. 6a). Shear strain at the rock glacier margins is particularly evident at diamonds A, D, G and J, where the maximum (extensional) principal strain axes are ‘rotated inward’ 22–50° from the flow direction and side of the rock glacier. Of the diamonds near the margins, only diamond F does not show evidence of such shear. Down-valley flow measurements (Fig. 6f) also indicate that there is little shear at this site.
Strain rates
Strain rates found in this study were at the low end of the range of rates determined photogrammetrically for Swiss rock glaciers (Reference Haeberli, King and FlotronHaeberli and others, 1979; Reference Kääb, Haeberli and GudmundssonKääb and others, 1997, Reference Kääb, Gudmundsson, Hoelzle and Allard1998). This is not surprising in view of the low overall flow velocity of Spruce Creek rock glacier, which is similarly at the low end of the range determined for the Swiss rock glaciers. Relatively high strain rates at the rock glacier are associated with either overall higher velocity or localized large differential velocities. On the upper portion of the rock glacier, 15 year averaged velocities (Table 3) are about 35% higher than on the lower part of the rock glacier, and maximum strain rates (Fig. 6c and d) are 2–3 times as high. On the lower part of the rock glacier, highest strain rates occur, not where overall velocities are highest, but where the faster-moving upper portion of the rock glacier is impinging on the lower portion (diamonds E and F).
The overall decrease in strain rate during the second half of the survey period was associated with a slowing of the upper part of the rock glacier and a decrease in the rate of differential movement between the upper and lower portions of the rock glacier (Table 3). It is unclear why the reduction in strain rate was limited to the central and northern portions of the rock glacier, while strain rates along the southern margin increased.
There are several possible explanations for the low overall flow velocities and strain rates.
-
1. Low rates may reflect the low slope of the rock glacier, an explanation consistent with the observation that longitudinal strain state at the rock glacier is closely related to slope variations. Reference Frauenfelder, Haeberli, Hoelzle, Phillips, Springman and ArensonFrauenfelder and others (2003) have argued, however, that there is little correlation between average slope of a rock glacier and its surface velocity.
-
2. Reference Frauenfelder, Haeberli, Hoelzle, Phillips, Springman and ArensonFrauenfelder and others (2003) suggest that temperature may be the dominant control on flow rate. Following Reference Hoelzle, Wagner, Kääb, Vonder Mühll. and AllardHoelzle and others (1998), they suggest that internal (‘ground’) temperature is the key control, but their data show a strong relationship between mean annual air temperature (MAAT) at the rock glacier terminus and flow velocity, with all rock glaciers with MAAT <–3°C having mean flow velocities <10 cm a–1. Low flow velocities at Spruce Creek rock glacier, where MAAT is approximately –4°C, are consistent with this observation.
-
3. Low flow rates may reflect the internal structure, if deformation is limited to an ice-rich upper portion of the rock glacier above debris-rich, non-deforming material (Reference Haeberli, Hoelzle, Kääb, Keller, Vonder Mühll, Wagner, Lewkowicz and AllardHaeberli and others, 1998). In the absence of information on the internal structure of Spruce Creek rock glacier it is not possible to evaluate this possibility.
-
4. Low rates may reflect recent stagnation of the rock glacier. Photogrammetric and lichen measurements indicate that flow has slowed by a factor of about five during the last century, possibly as a result of ice loss due to post-Little Ice Age temperature increase (Leonard and others, unpublished information).
Based on available data, it is not possible to determine what factor, or what combination of factors, is responsible for the current low flow and strain rates.
Transverse ridges
It has long been believed that transverse ridge and furrow systems on rock glaciers are products of compressing flow, generally related to down-glacier decreases in surface slope (Reference Wahrhaftig and CoxWahrhaftig and Cox, 1959; Reference Loewenherz, Lawrence and WeaverLoewenherz and others, 1989). Steel-tape measurements by Reference White, Giardino, Shroder and VitekWhite (1987) across a series of transverse ridges at Arapaho rock glacier, Colorado, confirmed that longitudinal shortening was occurring across the ridges. Reference Kääb, Gudmundsson, Hoelzle and AllardKääb and others (1998) also confirmed the association of transverse ridges with compressing flow and decreased surface slope at Murtèl rock glacier, Switzerland. However, they also noted that the relationship between compression and transverse ridge development was not simple and that up-glacier areas of compressing flow did not exhibit transverse ridges.
Data from Spruce Creek confirm both the general association of transverse ridges with slope decrease and compressing flow, and the lack of a one-to-one correlation. Transverse ridge/furrow systems are well developed only in the middle portion of the rock glacier (Fig. 2) near strain diamonds D, E and L, an area of strongly compressional flow where (1) there is a significant down-glacier reduction in slope and (2) the more rapidly flowing upper portion of the rock glacier impinges on the slower lower portion. Where transverse ridges are well developed, they are approximately perpendicular to the calculated direction of greatest shortening (Table 4). Transverse ridges are absent or poorly developed in areas of extending flow, but also in the area of compressing flow at the head of the rock glacier (near diamond I) and in some mid-rock-glacier areas where flow is strongly compressional (near diamonds F and L). It is unclear why transverse ridges are well formed in some areas of compressing flow but not in others. The difference does not appear to be related to either rate of longitudinal shortening or the differential strain rate (Table 4). Occurrence of transverse ridges is also not related purely to position down-glacier, which might reflect a progressive down-glacier increase in total magnitude of shortening (Ka¨a¨b and others, 1998).
Table 4. Relationship between transverse ridges and shortening strain. Numbers in parentheses are 95% certainty ranges

Conclusions
Patterns of strain at Spruce Creek rock glacier are related primarily to changes in surface slope, with longitudinal extension resulting from down-glacier increases in slope, and longitudinal shortening from down-glacier slope decrease. This pattern is modified by shear along the sides of the rock glacier. It is also complicated by the presence of two slightly faster-moving lobes in the upper section of the rock glacier that appear to be impinging on a slower-moving lower section, resulting in a broad middle zone of longitudinal shortening. Strain rates are relatively high in the upper, faster-moving portion of the rock glacier and in the mid-rock-glacier zone of longitudinal shortening, and relatively low in the lower portion of the rock glacier. During the survey period, the velocity difference between the upper and lower portions of the rock glacier decreased, due primarily to a reduction of flow in the upper area, a change accompanied by an overall decrease in strain rate. This slowing of the upper portion of the rock glacier is consistent with a previously noted reduction of flow velocities since the mid-20th century (Leonard and others, unpublished information).
Analysis of strain in portions of the rock glacier with well-developed transverse ridges confirms the general association of such features with longitudinal shortening. However, as previously suggested by Reference Kääb, Gudmundsson, Hoelzle and AllardKääb and others (1998), the relationship between longitudinal shortening and transverse ridge development is not simple, and in several areas of strong shortening, no transverse ridges have developed.
Acknowledgements
S. Janke got us started thinking about statistical analysis of strain measurements. L. Vierling produced surface profiles of the rock glacier, under the guidance of J. Messerich at the US Geological Survey photogrammetry laboratory in Denver, Colorado. W. Haeberli and B. Hubbard provided very helpful reviews of the manuscript. More than a dozen Colorado College undergraduate geology students assisted us in the field.














