Introduction
Glaciers are important for storage of water resources (Reference Jansson, Hock and SchneiderJansson and others, 2003). Changes in long-term storage from climate change are of interest to, for example, water-stressed societies that depend on glacier melt for agricultural production. Hence, providing accurate glacier mass-change estimates (Reference Dyurgerov and MeierDyurgerov and Meier, 1997) becomes important and with that mass-balance determination on reference glaciers (Reference Fountain, Jansson, Kaser and DyurgerovFountain and others, 1999). This paper deals with the contribution of so-called internal accumulation to glacier mass balance.
Internal accumulation can be defined in two ways. It can be viewed as mass added to the firn by freezing percolating water and water trapped in temperate firn. This is the definition commonly used for mass-balance work (Reference Trabant and MayoTrabant and Mayo, 1985; Reference Østrem and BrugmanØstrem and Brugman, 1991) since it involves mass added to the glacier that would escape detection by traditional mass-balance measurement techniques. However, from the point of view of an energy-balance approach, internal accumulation can also comprise water refreezing in the annual snowpack. This water is generated by melting at the snow surface but may re-freeze lower down only to again be subject to melting at a later stage of a melt season. Hence such water is melted several times and may be accounted more than once when comparing mass loss to melt potential. The term internal accumulation is thus ambiguous between disciplines.
In this paper, we define internal accumulation as ice formation within a glacier due to freezing of liquid water that is not accounted for by traditional mass-balance measurements. Hence, internal accumulation is produced through two processes: (1) freezing of percolating water in cold snow and firn, and (2) freezing of water trapped by capillary action in snow and firn by the winter cold. This formation becomes significant for mass balance when the winter cold wave in the accumulation area penetrates below the summer surface of the previous year and when the firn layer is warmed to temperate conditions through refreezing of percolating water in summer. Internal accumulation introduces a systematic error into the mass-balance calculation, and methods to determine whether the contribution is significant or not need improvement.
Internal accumulation and superimposed ice formation are caused by the same processes. Whereas superimposed ice forms above the previous year’s summer surface and hence does not evade accounting in standard mass-balance measurements (Reference Østrem and BrugmanØstrem and Brugman, 1991), internal accumulation occurs below the previous year’s summer surface and hence adds to mass accounted for during past mass-balance measurements but not accounted for during the year in question. Hence this adds mass to a glacier which by standard techniques (Reference Østrem and BrugmanØstrem and Brugman, 1991) is considered lost through ablation.
Internal accumulation was recognized in many early studies (Reference Hughes and SeligmanHughes and Seligman, 1939; Reference Ahlmann and EriksonAhlmann and Eriksson, 1946; Reference ShumskiiShumskii, 1964) but was often regarded as insignificant for mass balance. Often, only refreezing of percolating water was considered (Reference PatersonPaterson, 1994). Reference Trabant and MayoTrabant and Mayo (1985) extended the work of Reference BazhevBazhev (1973) and developed a method for estimating internal accumulation from minimum firn temperature at the snow–firn interface. Trabant and Mayo found that internal accumulation contributed 7–64% of the annual accumulation on Alaskan glaciers and that internal accumulation occurs in all glaciers with water percolation and seasonal negative temperature in the firn layer. Reference Trabant and BensonTrabant and Benson (1986) estimated internal accumulation together with superimposed ice formation on McCall Glacier, Alaska, to ~40% of the annual net accumulation for the years 1969–72.
Our aim was to improve on methods of quantifying internal accumulation in firn and to determine its significance for the mass balance of Storglaciären. Storglaciären (Fig. 1) is a small polythermal valley glacier in northern Sweden with a cold surface layer in the ablation area (Reference Pettersson, Jansson and HolmlundPettersson and others, 2003). The cold surface layer is analogous to permafrost, and results from a negative energy balance at the glacier surface. In the accumulation area, the cooled surface layer can easily be warmed to melting temperature each year through percolation and refreezing of surface meltwater (Reference SchneiderSchneider, 2001), thus maintaining the accumulation area of the glacier under temperate conditions. Detailed mass-balance measurements have been carried out since 1946 (Reference Holmlund and JanssonHolmlund and Jansson, 1999). Reference Fountain, Jansson, Kaser and DyurgerovJansson (1999a) estimated uncertainties in measured variables on the calculated mass balance to be ~0.1 m w.e. Reference Östling and HookeÖstling and Hooke (1986) calculated refreezing of percolating water from the cold content of the snow layer on Storglaciären in spring (Reference Hooke, Le, Brzozowski and BrongeHooke and others, 1983) to 0.02 m w.e. However, they did not consider refreezing of capillary water during winter. Reference HolmlundHolmlund (1987) used the term internal accumulation for the spring component only and estimated refreezing of percolating water from mean values of air temperature, mass balance and firn density to 0.03 m w.e. (2% of annual winter balance, b w).

Fig. 1. Location map of Storglaciären (67.9°N, 18.5°E) showing locations of temperature measurements and core drillings.
Accurate determination of internal accumulation requires information on both temperature and water content in the firn layer. Therefore, we measured temperature profiles in several boreholes in the accumulation area; physical characteristics and water content of firn were determined from a firn core. We obtained values for internal accumulation of 0.04–0.06 m w.e. (3–5% of b w), indicating that the contribution of internal accumulation in firn may be of similar magnitude to that in snow. Although the annual contribution of internal accumulation to the mass balance of the glacier is small, its systematic nature indicates a significant influence in the longer term.
Theory and Processes of Internal Accumulation
Internal accumulation, b I, occurs by two processes: refreezing of percolating meltwater in cold firn, b p, and freezing of water held by capillary forces, b c. (Terminology and abbreviations in the following largely follow Reference Mayo, Meier and TangbornMayo and others (1972) and Reference Trabant and MayoTrabant and Mayo (1985).) Thus, b I can be described by
b I = b p + b c.
b p is the maximum internal accumulation for a given temperature profile and given by
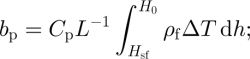
b c is calculated from the irreducible water content by
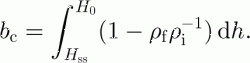
In Equations (1) and (2), ρ f is firn density, ρ i is ice density, C p is specific heat of ice, ΔT is temperature increase in K at depth h, due to refreezing of percolating water, L is latent heat of fusion of ice, H sf is the depth of the snow–firn interface, H ss is the depth of the previous year’s summer surface, H 0 is the maximum depth of the 0°C isotherm at the end of winter and S wi is irreducible water saturation, which is the volume of water divided by pore volume when all free water drained the firn.
Firn porosity, n, is the ratio of pore volume to total volume. It can be calculated from firn density, ρ f, and gravimetric water content, θ m, by
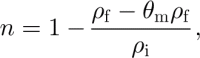
where θ m is defined as the ratio between the mass of liquid water in the firn and the mass of the total firn sample and ρ i is density of ice. When all free water has drained, the remaining water is held in firn, against gravity, by capillary and adhesive forces; this is called irreducible water content, θ mi. According to Equation (2), S wi is needed to calculate the capillary component of internal accumulation. S wi can be calculated from θ mi as
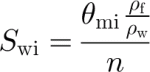
where ρ w is density of water. Equation (2) differs from the definition of Reference Trabant and MayoTrabant and Mayo (1985) who used H sf as the upper boundary of the active layer for both components of internal accumulation. Reference Trabant and MayoTrabant and Mayo (1985) did not consider that liquid water in the annual snow layer is determined as part of the summer balance when density is measured in fall.
To visualize the processes acting in the firn area, we can use the following conceptual model. In spring, a cold, dry snow-and-firn cover overlies a temperate firn layer (Fig. 2a). There is no free water. In late spring–early summer, temperature in the firn layer rapidly rises to 0°C from the heat released as percolating meltwater refreezes (Fig. 2b). Due to refreezing of percolating meltwater in the layer between H sf and H 0, additional ice is accumulated which was not measured by normal mass-balance methods (Reference Østrem and BrugmanØstrem and Brugman, 1991). The cold content of the firn layer determines the magnitude of this component (Equation (1)). Surplus meltwater is trapped in small pores, veins and three-grain intersections (Fig. 2c). Melting continues and water saturation in the firn layer rises from 0 at the end of winter (Fig. 2a) to S wi in early summer (Fig. 2c). When water saturation exceeds S wi, an outflow of water from the firn layer starts (S w≽S wi). In fall (Fig. 2c), water input at the surface ceases, all movable water drains, and water saturation reaches its minimum, S wi. Summer balance is determined in fall (Fig. 2c) and snow density is measured down to the depth of the previous year’s summer surface, H ss. Trapped capillary water in the snow layer is part of measured snow density and does not need to be considered for internal accumulation. Capillary water below H ss down to H 0, on the other hand, is not measured. This water freezes during the following winter (Fig. 2d) and thus contributes to accumulation. The mass of internally accumulated capillary water is calculated using Equation (2). At the end of the following winter a new cycle of refreezing of percolating meltwater, firn warming and wetting and refreezing of capillary water starts. The active layer of internal accumulation can undergo several cycles until it leaves the zone of subfreezing temperatures. Refreezing of capillary water below the previous year’s summer surface extends the mass-balance year to the following winter, and the annual layer to the depth of the 0°C isotherm.

Fig. 2. Processes of internal accumulation in firn of a temperate glacier. Sw is the water saturation; Swi is the irreducible water saturation; T is the firn temperature; Hsf is the depth of the snow–firn interface; Hss is the depth to the previous year’s summer surface; H0 is the depth to the temperate snow or firn. See text for a detailed explanation.
As mentioned above, H sf and H 0 delimit the active layer of internal accumulation. This is different along the firn line, which is where the transition between firn and ice emerges on the glacier surface. In this zone, maximal firn depth, H, is smaller than H 0, and confines the active layer. The accumulation area can thus be divided into an area of maximum internal accumulation A max, in which H>H 0, and an area with reduced internal accumulation A red, where H ≼ H 0 (Fig. 3). Total internal accumulation in firn,
was estimated by
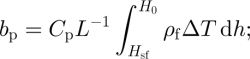
where A is the total area of the glacier.

Fig. 3. Active layer of internal accumulation along a profile across the firn limit. H is total firn depth and the firn limit is the line where the firn–ice transition emerges at the glacier surface, H sf is depth of snow–firn interface and H 0 is depth of the 0°C isotherm.
Methods
In order to estimate the contribution of internal accumulation to the mass balance of Storglaciären, we need to establish the necessary parameters for Equations (1) and (2) and apply the calculations to the entire accumulation area. Because of the complexity of the measurements needed to establish the internal accumulation at a point, we have concentrated on careful sampling at one site and investigated how these measurements can be extrapolated for the accumulation area.
Water content
In order to determine internal accumulation, firn samples must be collected just before surface melting and percolation of water commence. Two firn cores were therefore drilled at site 29 (Fig. 1) in May 1998 and 1999, a few weeks before melting started in each year. A Polar Ice Coring Office (PICO) auger was used, obtaining a 7.5 cm diameter core. The cores were weighed immediately after drilling with a digital scale (±1 g) to determine density.
Because the active layer of internal accumulation (Fig. 2) was frozen, water content could not be determined in this layer. Water content in snow decreases with decreasing porosity (Reference Coléou and LesaffreColéou and Lesaffre, 1998). As porosity usually decreases with depth, water content measured just below the 0°C isotherm should thus yield a minimum value for the water content in the active layer.
Measurements of water content and porosity are difficult. The most critical point for measuring the free-water content of temperate firn is that the temperature has to be kept at 0°C throughout the analysis. To minimize melting of ice or freezing of free water, analyses must be carried out in the field. Due to such problems, only the 1999 core could be used to determine water content. Reference ColbeckColbeck (1978) reviewed different methods and showed through an error analysis that only direct measurements of liquid volume gave reasonable results and that, for example, calorimetric measurements were inaccurate. Today, methods based on time-domain reflectrometry and microwaves are reliable enough for measuring liquid-water content in snow (Reference Schneebeli, Coléou, Touvier and LesaffreSchneebeli and others, 1998) but they are not suited for measurements in boreholes or on firn cores.
Liquid-water content in firn in the present investigation was determined by adapting a dilution method originally developed for snow (Reference Davis, Dozier, LaChapelle and PerlaDavis and others, 1985). An aqueous salt solution is diluted when mixed with wet snow or firn.
The change in concentration is the base for the measurements. The temperature of all tools and solutions was held constant at 0°C (±0.1°C) by placing them in plastic bottles in an ice bath. A section of a firn core (3×20 cm) of mass m f was crushed with a wooden stick in a 1.5 L stainless-steel thermos bottle. The firn sample was weighed with a digital scale with an accuracy of 0.01 g. A stock solution (0.01 N HCl) of mass m s and of known impurity concentration, c s, was mixed thoroughly for 30–60 s with the firn sample and was diluted by the liquid water in the sample. The mixed solution was decanted into a plastic beaker and extracted using a syringe with a 40 μm filter to eliminate small ice grains. The impurity concentration of the mixed stock solution, c m, was then measured. The gravimetric liquid-water content of the firn sample, θ m, was then calculated as
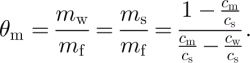
Concentration was determined from electrical conductivity, κ, of the solution measured with a standard conductivity meter (WTW Lf 340). Conductivity depends on temperature and is not linear to the concentration of HCl. All measurements were carried out at 0°C and the measurements were normalized to 25°C automatically by the conductivity meter. The relationship between concentration ratio and conductivity ratio is

The exponent, q, was determined from tables to be 1.0133 for HCl in the concentration range 0.005–0.01 N and a temperature of 25°C (Reference Hammer and DeWaneHammer and DeWane, 1970). Electrical conductivity of liquid water stored in the firn, κ w, was 10–3 mS–1, whereas electrical conductivity of the stock solution and the diluted stock solution, κ s and κ m, were in the region of 4.8 mS cm–1, resulting in c w/cs<0.002, whereas c m/cs ~ 0.95. Accordingly, the term c w/cs in Equation (6) could be neglected.
Temperature measurements
Firn temperature was measured continuously in 1 m intervals along a vertical profile by type-K thermocouples and a Campbell Scientific CR10 data logger from May 1997 to December 1999 (29 in Fig. 1). A reference temperature was measured with a Campbell Scientific T107 probe with an accuracy of ±0.2°C. In addition, temperature was measured in several boreholes in the firn area in spring 1998 and 1999 (Fig. 1). These boreholes were drilled with a steam drill (Reference HeuckeHeucke, 1999) and had a diameter of ~3.5 cm. A platinum thermistor (Pt100) was lowered into the hole and pressed against the hole wall by a spring. Temperature was measured with an accuracy of ±0.1°C in 0.2–1 m intervals to determine the depth of the 0°C isotherm.
Air temperature was measured at 28S3 (Fig. 1) with a Pt100 thermistor and a Campbell Scientific CR10 data logger during the periods May–November 1997 and May–October 1998 and 1999. The measurements during the available winter months, September, October and May, were correlated with air temperature at Tarfala Research Station (TRS). The regression equation was used to estimate mean winter air temperature in the accumulation area. The site could not be occupied during the remaining months because of the accumulating snow and logistic difficulties in regularly visiting the site.
Firn limit and firn depth
According to Equations (1) and (2) H ss, H sf and H 0 must be known to calculate internal accumulation. H 0 was determined from the firn temperature profile. H ss and H sf were determined from snow probings and stake readings carried out by the TRS.
In order to use Equation (5), the firn–ice transition depth must be determined. Minimum water level in spring, which can be used as a measure for the firn–ice transition (Reference FountainFountain, 1989), was determined in several boreholes at location 29 to ~18.5 m below the snow surface. These point measurements were augmented by ground-penetrating radar measurements to determine the spatial distribution of the firn–ice transition. The radar sounding profile from stake 29 to stake 20 (Fig. 4) shows several radar reflections, which are caused by variations in density, firn structure and water content. The white line follows a layer, which could be the firn–ice transition. It correlates with minimum water level at 29 and the depth where firn density reached 850–900 kg m–3 (Fig. 5). The layer intersects the 0°C isotherm ~400 m down-glacier of stake 29 and emerges at the surface just above stake 20 (Fig. 4).

Fig. 4. Altitude, snow depth, 0°C isotherm and depth to firn–ice transition along a profile 29–20. Firn depth was derived from a radar sounding profile (Reference Richardson-NäslundRichardson-Näslund, 2001). See text for more details.

Fig. 5. Firn density, ρ, at location 29 in 1998 (C1-98) and 1999 (C2-99). IL is ice lens; WL is water level in the bore-hole. H sf and H 0 shows the approximate depth of the snow–firn interface and the penetration depth of the winter cold wave, respectively.
The location of the firn limit was determined from aerial photographs taken in 1998 and 1999. Note that the firn limit is not the annual snowline. The firn limit is similar to the mean equilibrium line when the glacier is in balance with the present climate. On a glacier with negative mass balance, the snowline is located higher than the firn limit, and vice versa on glaciers with positive mass balance. The firn-free areas are shaded dark in Figure 6. The firn area is ~49% of the total glacier area. The mapping shows that the radar profile was located in a corridor of firn between areas of net mass loss, which explains the shallow firn depth (Fig. 4). The reflecting layer in the radar image changes inclination ~150 m from the firn limit. Using this inclination in Figure 3, the horizontal distance between the firn limit and the border between A max and A red was estimated to be 100 m. A 100 m transition zone was then drawn around all firn-free areas (light shaded in Fig. 6) in which H < H 0. The remaining firn area (white) is where H > H 0 and where internal accumulation was not limited by the firn–ice transition.

Fig. 6. Areas of maximum, reduced and no internal accumulation on Storglaciären. Firn limit determined from aerial and terrestrial photographs in August 1998 and September 1999.
Results
Water content
Densities of the firn cores drilled in different years, C1-98 and C2-99, were relatively similar (Fig. 5). Both cores showed frequent ice lenses, with no systematic increase of ice lenses with depth. S wi and n were calculated according to Equations (4) and (6). Porosity decreased with depth due to increasing overburden pressure and progressive snow metamorphism (Fig. 7). Gravimetric water content varied between 2% and 6%, with higher values above ice lenses than below, but with no systematic correlation with porosity. Water saturation increased from ~8% just below the 0°C isotherm to 50–80% in the water-saturated part of the firn. In zones with ice lenses, water saturation was generally higher. Constant water content with depth, combined with decreasing porosity, leads to increasing water saturation (Fig. 7; Equation (4)). The firn in the zone of the active layer (~4.5–12 m; Fig. 5) had a density of 600–750 kg m–3, which corresponds to a porosity of 0.18–0.35 when ignoring free water (Equation (3)). Using the results above (Fig. 7), θ m is 4–7%, which compares to a volumetric water content (pore volume divided by total volume) of 2–3% or a water saturation of 6–8% (Equation (4)).

Fig. 7. Firn density, ρ, porosity, n, gravimetric water content, θm, and water saturation, Sw, in core C2-99 at location 29, Storglaciären, May 1999. Ice lenses are shown as shaded areas.
Irreducible volumetric water content of dense snow (550–600 kg m–3) reaches its minimum at 2–3% of unit volume (Reference LemmeläLemmelä, 1973) which corresponds to a water saturation of about 7% (Reference ColbeckColbeck, 1974). Irreducible water content decreases with decreasing porosity. Reference Coléou and LesaffreColéou and Lesaffre (1998) investigated repacked homogeneous snow with porosity of 0.7–0.4 and found that between irreducible gravimetric water content, θ mi, and porosity, n, there was a relationship of θ mi = 0.0143e3.3022n . Figure 8 shows the results of the present investigation in comparison with the results of Reference Coléou and LesaffreColéou and Lesaffre (1998). It is evident from this graph that irreducible water content is higher in firn than in snow. This can be explained by retention of water in smaller firn pores which manage to hold more water against gravity because of a larger capillary force, or water in isolated pores which cannot drain. However, no systematic change in water content with porosity was found within the firn layer. This indicates that probably microstructure and degree of connectivity between pores and not porosity are the governing factors for water drainage and retention processes in firn.

Fig. 8. Irreducible water content, θmi, and porosity, n. Snow data from Reference Coléou and LesaffreColéou and Lesaffre (1998) (open circles) and firn data from core C2-99 at location 29 on Storglaciären at 11.5–18.6 m depth (filled circles).
At 18.8 m the firn at C2-99 was water-saturated (Fig. 7). The minimum water level at the end of winter is often taken as the firn–ice transition (Reference FountainFountain, 1989), which is the depth at which firn becomes practically impermeable. This concept assumes that water which is not retained in the firn due to capillary forces drains from the firn layer. During drilling through the firn into underlying impermeable ice, water in the borehole cannot escape and water level indicates the firn–ice transition. In both firn cores (Fig. 5) this level coincides with the depth at which density reaches 830–850 kg m–3, which is the theoretical value for pore close-off (Reference PatersonPaterson, 1994).
Temperature
Firn temperature (Fig. 9) was measured in the southern cirque of the accumulation area (Fig. 1); no temperature measurements are available from the northern cirque. Cooling of the firn layer during winter is forced by the temperature gradient in the firn, which mainly depends on air temperature and snow depth. Air temperature was derived from measurements at TRS by establishing a rating equation from simultaneous measurements at 28S3 during parts of the investigation period. 28S3 is located at ~1500 ma.s.l. and TRS at 1130 m a.s.l., giving an altitude difference of 370 m. The mean temperature difference between 28S3 and TRS during the period of simultaneous measurements was 1.7°C, which results in a temperature lapse rate of –0.46°C / 100 m in altitude. Extending this lapse rate to the northern cirque (~1600 m a.s.l.), air temperature was ~0.5°C colder than in the southern cirque. From Figure 10 we can estimate that a temperature decrease of 0.5°C would cause the 0°C isotherm to penetrate 0.2–0.5 m deeper. Mean snow depth in the northern and southern parts of the accumulation area was 4.4 and 3.1 m, respectively (Reference Fountain, Jansson, Kaser and DyurgerovJansson, 1999b). As shown in Figure 11, higher snow accumulation reduces cold-wave penetration. This can be explained by a smaller temperature gradient in the firn layer due to a larger distance between snow surface and the 0°C isotherm. However, it must be remembered that the forcing occurs while the snow-pack is accumulating and that the temperature at the transient snow surface and in the new snow is part of this forcing. The effect of lower air temperature at higher altitude, as described above, can be partly compensated by a lower heat flux due to higher accumulation. In the same way, large temperature gradients in firn layers with lower accumulation at lower altitudes are compensated by higher air temperature. Mean snow depths at measurement sites 29 (4.5 m) and 28S3 (3.2 m) were in same range as the mean values for the southern and northern cirques. It therefore seems justifiable to assume that the firn temperature profile in the northern cirque was similar to those measured at location 29, only yielding lower temperature. The two averaged temperature profiles (Fig. 9) therefore represent minimum and maximum temperature profiles, respectively, of the firn area.

Fig. 9. Late-winter firn temperature profiles, 1997–99. Hsf is depth below snow–firn interface (Fig. 2). Filled circles are firn temperature profiles from five different boreholes around location 29 (1997–99); triangles are measurements from bore-holes 27S2, 27S4, 29S4, 28S3 and B. Different boreholes were measured in different years (see Fig. 1).
Firn temperature was plotted against depth below the snow–firn interface (Fig. 9). Results from locations in the central part of the investigation area (28S3 in Fig. 1) gave a cold-wave penetration depth into firn of 7.9–8.3 m, whereas penetration depth at location 29 was 6.6–7.0 m (Fig. 9).
The effect of maximum snow depth on cold-wave penetration depth was investigated using mean values of the boreholes around 29 and in the center of the southern cirque respectively. Results show no clear functional relationship between penetration depth and snow depth (Fig. 11). However, the cold wave penetrated significantly deeper into the firn layer in the central part of the cirque around location 28S3 than at location 29 (Fig. 1). Mean air temperature calculated for different periods during winter was tested for correlation with mean cold-wave penetration depth. Mean air temperature of the entire winter (September–May) gave the best results, indicating a relationship where cold-wave penetration increased with decreasing air temperature (Fig. 10).
Internal accumulation
Internal accumulation was calculated from the two averaged temperature profiles presented in Figure 9, a water saturation of 6–8% and a density profile calculated as the arithmetic mean of both measured profiles (Fig. 5). b I was on the order of 0.09–0.16 m w.e. (Fig. 12). b p was 30–50% of b c (Table 2).

Fig. 12. Internal accumulation, bI, on Storglaciären at location 29 and 28S3 in relation to irreducible water saturation, Swi. bI was calculated from the temperature profiles in Figure 9 and Swi of 6–8%.
Total internal accumulation was calculated using Equation (5) with the data in Tables 1 and 2. Depending on S
wi, the temperature profile and
![]() was 0.04–0.06 m w.e. Adding these results to measured accumulation (Reference Fountain, Jansson, Kaser and DyurgerovJansson, 1999b), total internal accumulation in firn accounted for 3–5% of annual accumulation of the entire glacier.
was 0.04–0.06 m w.e. Adding these results to measured accumulation (Reference Fountain, Jansson, Kaser and DyurgerovJansson, 1999b), total internal accumulation in firn accounted for 3–5% of annual accumulation of the entire glacier.
Table 1. Areal extent of the accumulation area, and area of maximum (Amax) and reduced (Ared) internal accumulation on Storglaciären, September 1998. Corresponding areas are shown in Figure 6

Table 2. Internal accumulation on Storglaciären. bw is winter balance, Hss is snow depth, bp is the percolation component and bc the capillary component of internal accumulation, and Swi is irreducible water saturation. Locations 29 and 28S3 are shown in Figure 1

Reference Trabant and MayoTrabant and Mayo (1985) developed a method to estimate internal accumulation from minimum temperature at the snow–firn interface, T sf. From Figure 9, T sf can be determined as –3.5 to –5°C. Using this value and the method of Reference Trabant and MayoTrabant and Mayo (1985) yields a b c of 0.11–0.15 mw.e. and a b p of 0.03–0.04 m w.e. The value of capillary refreezing calculated with Trabant and Mayo’s method is higher than the results from measured data given above. Trabant and Mayo considered that water in the previous year’s snow layer is not measured when summer balance is determined in autumn, and that it therefore does not contribute to that internal accumulation which influences mass balance.
Our calculations show that air temperature, maximum snow depth in winter and minimum snow depth in summer are the main parameters determining internal accumulation. This is true if (1) thermal properties and water-holding capacity of the firn layer can be assumed stable from one year to another, and (2) the extent of the firn area is stable if the glacier is in near-steady state. Winter temperature at TRS and the mass balance of Storglaciären in 1997/98 were compared with the mean values of the period 1965–99 (Reference Grudd and SchneiderGrudd and Schneider, 1996; Table 3). Both temperature and mass-balance parameters in 1997/98 and 1998/99 are similar to the respective mean values for the period 1965–99. The results from 1997/98 and 1998/99 can therefore be regarded as representative of internal accumulation in the firn of Storglaciären for the mentioned period, 1965–99. Under current climate conditions, traditional mass-balance methods underestimate accumulation on Storglaciären by ~0.05 mw.e. due to internal accumulation in firn. Even if this result is within the uncertainty of measured mass-balance parameters (±0.1 mw.e.; Reference Fountain, Jansson, Kaser and DyurgerovJansson, 1999a), it underestimates accumulation systematically. An additional source for underestimating accumulation is the formation of superimposed ice in the ablation area. Superimposed ice formation on Storglaciären in the area of the equilibrium line accounted for 10% of annual accumulation in 1948 and 1949 (Reference SchyttSchytt, 1949). Superimposed ice below the equilibrium line can easily be distinguished from glacier ice, but superimposed ice that forms at the bottom of the firn layer just above the equilibrium line is difficult to recognize since it is not visible and contributes to even larger errors (Reference Trabant and BensonTrabant and Benson, 1986). Detailed snow probings and stake readings could help to identify this source of accumulation.
Table 3. Winter temperature (September–May), Tw, at TRS, and annual winter balance, bw, and annual net balance, bn, of Storglaciären

The significance of internal accumulation for glacier mass balance depends on the areal extent of the accumulation area, the thickness of the active layer and the winter air temperature. Glaciers with a positive mass balance have high accumulation or low ablation (or both) due to large winter precipitation or low summer temperature. On such glaciers, a growing accumulation area results in a larger areal extent of the active layer. A thicker firn layer increases the area of maximum internal accumulation. At the same time, higher accumulation insulates the firn layer and decreases cold-wave penetration. Falling winter temperatures would compensate this insulation effect. In addition, due to low ablation, the remaining snow layer at the end of summer becomes thicker which decreases the active layer because a larger part of the firn layer is measured when determining summer balance. To summarize, the active layer becomes spatially more extensive and thinner on glaciers with increasing accumulation or decreasing ablation rates (or both), holding winter temperature constant. With lower winter temperature, internal accumulation will increase overall.
Glaciers with a negative mass balance have low accumulation and high ablation due to low winter precipitation or high summer temperature or both. Consequently, the accumulation area diminishes. Steady winter temperatures and low accumulation rates cause the cold wave to penetrate deeper. However, raising temperature compensates this effect. High ablation rates diminish the annual snow layer, which increases the active layer of internal accumulation. On retreating glaciers the active layer becomes spatially smaller but thicker. With increased winter temperatures, internal accumulation will decrease.
Conclusions
Internal accumulation has two components: (1) refreezing of percolating meltwater in cold firn in spring and (2) re-freezing of retained water due to capillary forces in firn during winter when the cold wave penetrates into the firn layer. The magnitude of internal accumulation therefore depends on firn temperature and irreducible water content. Firn temperature can be related to snow depth and air temperature where low accumulation and low air temperature cause the cold wave to penetrate deeper. This is explained by large temperature gradients in the firn layer and a corresponding high heat flux from the firn layer to the atmosphere. The 0°C isotherm is the lower boundary of the active layer for internal accumulation in areas where firn depth is larger than the 0°C isotherm. In the remaining area, along the firn limit, the active layer is confined by firn depth. Irreducible gravimetric water content in the firn of Storglaciä-ren was 2–3%, which corresponds to an irreducible water saturation of 6–8%. These values are slightly higher than those of compact snow, possibly due to retained water in isolated pores of the firn that cannot be drained. Internal accumulation in firn plays a significant role for the mass balance of Storglaciären. Traditional mass-balance measurements underestimate annual accumulation by ~0.05 m w.e. (~4%) when neglecting internal accumulation in firn under present climate conditions.
Acknowledgements
The staff of the Tarfala Research Station are gratefully acknowledged for their support in the field. C. Richardson-Näslund, K. Grust and M. Nyman assisted during the core drillings. C. Richardson-Näslund and R. Pettersson provided the radar images. P. Holmlund, S. Jonsson and A. Fountain made valuable comments on earlier versions of the manuscript. We especially thank R. Hock for providing valuable discussions and comments at all stages of this work. L. Stearns checked the language. Financial support was obtained from the Axel Hamberg Fund of the Royal Swedish Academy of Sciences, the André Fund of the Swedish Society for Anthropology and Geography, the Helge Ax:son Johnson Foundation, the Göran Gustafsson Foundation for the Environment and Research in Lappland, the Carl M:son Mannerfelt foundation, and the Lillemor and Hans W:son Ahlmann and Axel Lagrelius funds of Stockholm University. The comments of two anonymous referees improved the final paper.



















