1. INTRODUCTION
The decline in mass of the Earth's glaciers has profound implications for society, involving sea-level rise (Gardner and others, Reference Gardner2013; Vaughan and others, Reference Vaughan and Stocker2013) and water security in hydrologically vulnerable catchments (Jansson and others, Reference Jansson, Hock and Schneider2003; Vergara and others, Reference Vergara2007). In the context of climate change, there is consequently a pressing need to understand how glacier mass balance, and specifically melt, is coupled with climatic variability. For this purpose, models have been employed that adopt either a physical or empirical approach to simulating surface melting (Hock, Reference Hock2005 provides a review). Physical models resolve the surface energy balance (SEB) using principles of heat conservation (e.g. Hock and Holmgren, Reference Hock and Holmgren2005; Reijmer and Hock, Reference Reijmer and Hock2008; Rye and others, Reference Rye, Arnold, Willis and Kohler2010), whereas empirical methods seek statistical linkages between the melt rate and indices of meteorological variability (e.g. De Woul and Hock, Reference De Woul and Hock2005; Fealy and Sweeney, Reference Fealy and Sweeney2007; Rasmussen and others, Reference Rasmussen, Andreassen and Conway2007).
The greater physical realism of SEB approaches makes such techniques conceptually appealing, but data scarcity (both spatially and temporally) often prohibits their implementation. This is particularly true for studies that seek to simulate melt in a changing climate. For these applications, gridded output from general circulation models (GCMs) must be applied. Such data are spatially coarse, and do not resolve microclimatic variability in the topographically complex environments where glaciers reside. Hence, there is a mismatch of scale between GCM output and the information required to resolve the SEB (Machguth and others, Reference Machguth, Paul, Kotlarski and Hoelzle2009; Kotlarski and others, Reference Kotlarski, Jacob, Podzun and Paul2010; Mölg and Kaser, Reference Mölg and Kaser2011).
Empirical techniques, on the other hand, are not necessarily so compromised by this scale problem. The most popular methods for simulating melt empirically utilize the well-established correspondence between positive air temperatures and the melt rate (Braithwaite, Reference Braithwaite1981; Ohmura, Reference Ohmura2001; Sicart and others, Reference Sicart, Hock and Six2008). As a driving variable, air temperature varies slowly and predictably through space, and is therefore amenable to interpolation (Hock, Reference Hock2003), meaning that temperature-driven models are better placed to utilize spatially coarse GCM output. This attribute has seen global-scale melt simulations performed using ‘temperature-index’ methods to quantify sea-level rise for a changing climate (e.g. Raper and Braithwaite, Reference Raper and Braithwaite2006; Radić and Hock, Reference Radić and Hock2011; Marzeion and others, Reference Marzeion, Jarosch and Hofer2012, Radicć and others, Reference Radić2014).
A simple form of the temperature-index melt model can be written:
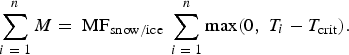 $$\mathop \sum \limits_{i\; = \; 1}^n M = \; {\rm MF}_{{\rm snow/ice\;}} \mathop \sum \limits_{i\; = \; 1}^n {\rm max}(0,\;T_i - T_{{\rm crit}} ).$$
$$\mathop \sum \limits_{i\; = \; 1}^n M = \; {\rm MF}_{{\rm snow/ice\;}} \mathop \sum \limits_{i\; = \; 1}^n {\rm max}(0,\;T_i - T_{{\rm crit}} ).$$
Hence, melt (M, mm w.e.) during the n-time intervals is calculated by multiplying the concurrent sum of temperatures (T, °C) above T crit (the threshold temperature above which melting occurs), by the scaling factor MF (mm w.e. t−1°C−1). The snow/ice subscripts in Eqn (1) indicate that different values of MF are applicable, depending on the classification of the melting surface. When a daily time step is used as the time interval and T crit = 0°C, the sum of air temperatures above T crit in Eqn (1) is termed the positive degree-day sum (PDD), and MF is known as the degree-day factor (DDF) (with units of mm w.e. d−1°C−1). The simplicity of Eqn (1) is a major attraction for melt simulations, and this appeal is made stronger given the good performance such models can achieve, sometimes exceeding the performance of data-demanding SEB models at the basin scale (Hock, Reference Hock2005).
1.1. Degree-day factors
Consistent with Eqn (1), DDF is defined:
That is, DDF is simply the total observed melt divided by the PDD accumulated during the same period. In interpreting Eqn (2), it is important to note that melt is a function of the SEB, which can be written:
where Q (W m−2) is the net balance of energy available, resulting in surface melting (if positive) or surface cooling (if negative). The subscripted Qs on the right-hand side of Eqn (3) denotes the k individual energy fluxes (W m−2). These are, respectively (from left to right): sensible heat, latent heat, net shortwave radiation, net longwave radiation, and the rain and subsurface heat fluxes.
Melt can be obtained from Eqn (3) by summing the contributions made by the k energy fluxes:
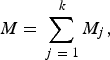 $$M = \mathop \sum \limits_{\,j\; = \; 1}^{\; k} M_j, $$
$$M = \mathop \sum \limits_{\,j\; = \; 1}^{\; k} M_j, $$
where melt quantities, M j , from the individual energy fluxes, Q j , are given by:
The Heaviside function, H(Q) adopts a value of 1 when the SEB (Q) is positive, and zero otherwise. Conversion from W m−2 to mm w.e. is achieved through dividing by L f (the latent heat of fusion, 334 kJ kg−1) and the number of seconds in the period over which melt is to be calculated, Δt.
Combining Eqns (2) and (4), DDF can be written:
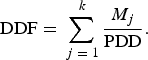 $${\rm DDF} = \mathop \sum \limits_{\,j\; = \; 1}^{\; k} \displaystyle{{M_j} \over {{\rm PDD}}}.$$
$${\rm DDF} = \mathop \sum \limits_{\,j\; = \; 1}^{\; k} \displaystyle{{M_j} \over {{\rm PDD}}}.$$
So it can be seen that each of the energy components contributes to the value of DDF, and importantly, static DDF is contingent upon the summed ratio of melt contributed by the individual energy fluxes to PDD remaining constant.
1.2. DDFs and climate change
Although degree-day melt models are generally lauded for their good performance and minimal data requirements, the use of temporally static DDF has been acknowledged as questionable. The relationship between PDD and the melt rate (Eqn (6)) will vary as different components of the SEB rise and fall in their relative importance with changes in the prevailing weather. This renders constant DDF unrealistic (Lang and Braun, Reference Lang, Braun and Molnar1990; Braithwaite, Reference Braithwaite1995; Hock, Reference Hock2003), and challenges the transferability of calibrated values in time and space (Macdougall and others, Reference MacDougall, Wheler and Flowers2011). However, an issue that has received relatively little attention is the long-term stability of DDF. It is argued here that such focus is very much required. For example, Huss and others (Reference Huss, Funk and Ohmura2009) observed a systematic decline in DDF during the latter-half of the 20th century in the European Alps, while Gabi and others (Reference Gabbi, Carenzo, Pellicciotti, Bauder and Funk2014) also found evidence for decreasing 20th-centuryDDF from modelling the mass balance of Rhonegletscher (Switzerland). Conversely, Braithwaite and others (Reference Braithwaite, Raper and Candela2013) used long-term mass-balance datasets to suggest that the temperature sensitivity of Alpine glaciers' had increased during the latter-part of the past half-century, while van den Broeke and others (Reference van den Broeke, Bus, Ettema and Smeets2010) noted an increase in DDF during the briefer 2003–07 period on the Greenland Ice Sheet.
Changes in the relationship between the temperature and melt rate are evidently to the detriment of melt simulations in a changing climate. If DDF is non-stationary with respect to the climate, then studies that seek to project melt (e.g. Flowers and others, Reference Flowers, Marshall, Björnsson and Clarke2005; Radić and Hock, Reference Radić and Hock2011; Marzeion and others, Reference Marzeion, Jarosch and Hofer2012), or those that attempt to hindcast past glacier balances using the degree-day model (e.g. Flowers and others, Reference Flowers2008; Engelhardt and others, Reference Engelhardt, Schuler and Andreassen2013) will be compromised by this behaviour. Thus, there is much need for research that addresses DDF variability explicitly, in order to shed light on the extent to which the assumption of a temporally constant DDF is valid.
2. AIMS
Considering the above, our aim here is to contribute to knowledge on the long-term (interdecadal) variability of DDF. We address this by examining an SEB series from Vestari Hagafellsjökull (detailed below), which permits any observed changes in DDF to be attributed to, and explained by, changes in the surface energetics. Because the 34 year period explored here overlaps that studied by Huss and others (Reference Huss, Funk and Ohmura2009), we additionally seek to compare our results with those of this earlier study, which observed a decline in DDF since the mid-1970s. Our coincident, more detailed record from Iceland contributes a much-needed insight into the possible extent of this behaviour.
3. DATA AND METHODS
To analyse DDF variability we used the 34 year SEB record presented by Matthews and others (Reference Matthews, Hodgkins, Gudmundsson, Pálsson and Björnsson2014a: they term this record ‘REANh’ in that study). Full details of how this dataset was produced are provided in the reference, so we only recap the main points here. SEB series were generated for two locations on Vestari Hagafellsjökull (an outlet of the Langjökull ice cap: Fig. 1) where Automatic Weather Stations (AWSs), maintained by the Institute of Earth Sciences (University of Iceland), are located. Situated at 500 and 1100 m, these AWSs are hereafter referred to as VH 500 and VH 1100, respectively. Further details of the meteorological campaign on Vestari Hagafellsjökull can be found in Guðmundsson and others (Reference Guðmundsson, Björnsson, Pálsson and Haraldsson2009) and Matthews and others (Reference Matthews2014b). SEB series were produced for these locations for June–August (JJA) 1979–2012 by using the 0.75° × 0.75° daily fields from the ERA-Interim reanalysis archive (Dee and others, Reference Dee2011) to force a physically based model. Such a long period of simulation permits low-frequency changes to the SEB to be assessed; in this instance allowing exploration of DDF stationarity. However, the reanalysis data do not capture the glacier microclimate and so must be downscaled before SEB modelling. Matthews and others (Reference Matthews, Hodgkins, Gudmundsson, Pálsson and Björnsson2014a) achieved this by implementing empirical quantile mapping to bias correct the incident radiative fluxes, air temperature, vapour pressure and wind speed relative to AWS reference series available for JJA 2001–2007 and 2001–2009 at VH 500 and VH 1100, respectively. As these bias correction functions are temporally invariant, their use assumes that the relationship between the local (AWS) and large-scale (reanalysis grid-point) climate does not change through time. This carries the implicit assumption that glacier hypsometry is temporally invariant. For example, changing elevation (e.g. from glacier thinning) would adiabatically modify the thermal and moisture properties of the local microclimate and could also impact insolation through changing shading patterns or slope. This complexity was neglected by Matthews and others (Reference Matthews, Hodgkins, Gudmundsson, Pálsson and Björnsson2014a). A summary of the resulting downscaled climate at our study sites is provided in Table 1.

Fig. 1. Location of study sites. (a) Shows Langjökull in a SPOT satellite image (a subsection from image GES 08-024, acquired 19th August, 2004), with map inset indicating Langjökull's position within Iceland. (b) Shows the position of the two AWSs, VH 500 and VH 1100 on Vestari Hagafellsjökull. Note the position of (b) is indicated on (a).
Table 1. Average meteorology during the period 1979–2012

± indicates 1 SD of daily means.
a Cloud cover is defined as the ratio of received to potential (top of atmosphere) incident shortwave radiation (calculated following Iqbal (Reference Iqbal1983)).
b Atmospheric emissivity is defined as the received incident longwave radiation divided by a blackbody radiator at the 2 m air temperature.
c Albedo is held constant during the hindcast and the values are prescribed based on averages measured at the AWSs during the JJA period 2001–07 (VH 500) and 2001–09 (VH 1100).
d Surface roughness is also held constant for the hindcast simulation.
The SEB was calculated at daily resolution from the bias-corrected reanalysis data by summing the sensible, latent, shortwave and longwave heat fluxes. Details as to how the energy components were computed in the model can be obtained from Table 2 in Matthews and others (Reference Matthews, Hodgkins, Gudmundsson, Pálsson and Björnsson2014a). The surface roughness lengths for momentum provided in that reference (and taken from Guðmundsson and others (Reference Guðmundsson, Björnsson, Pálsson and Haraldsson2009)) have been demonstrated as appropriate for our study sites by Matthews and others (Reference Matthews2014b), who highlighted that, when driven with in situ AWS data, the SEB model produced cumulative ablation estimates in agreement with those measured by echo-sounders within ranges of instrumental uncertainty. Albedo for the 34 year SEB simulation was held constant at the average values observed at the respective locations during the period of AWS observation (see Table 1). The uncertainty in simulating the SEB with the bias-corrected reanalysis data, rather than the in situ AWS data, was evaluated by Matthews and others (Reference Matthews, Hodgkins, Gudmundsson, Pálsson and Björnsson2014a; Table 5) by comparing their ‘REF’ (driven by AWS data) and ‘REANv’ (driven by reanalysis data) SEB series, and was reported as RMSEs. The uncertainty in melt totals translates to ±2.66 and 5.28% of mean annual melt at VH 500 and VH 1100, respectively.
Table 2. Contributions to the term dDDF/dt from the individual energy fluxes (see Eqn (6)) at VH 1100. se, t, and p, respectively denote the standard error, t-statistic and associated p-value for the regression coefficients used to approximate the derivatives (Section 3)

The SEB was simulated for the 34 year period using the bias-corrected reanalysis data under the assumptions of invariant glacier-surface conditions (hypsometry, albedo, surface roughness) and surface temperatures of 0°C. The resulting SEB record therefore represents potential melt energy, rather than actual energy balances over the past 34 years. This setup facilitates an examination of how the relationship between air temperature and the SEB varies as a function of the prevailing weather, without complications that arise from variable glacier surface conditions.
The DDF series were derived at annual (JJA) resolution via Eqn (2) using this potential melt record and PDD obtained from the bias-corrected reanalysis series. The albedo and roughness lengths selected for the SEB simulation mean that DDF should be interpreted as representing dirty ice and melting snow/firn at VH 500 and VH 1100, respectively (Table 1 and Matthews and others (Reference Matthews2014b)). This interpretation stays constant with time because the glacier surface is held constant throughout the hindcast. The uncertainty in DDF was estimated analogously to the uncertainty in SEB components, by calculating RMSEs between values derived from the ‘REF’ and ‘REANv’ series reported in Matthews and others (Reference Matthews, Hodgkins, Gudmundsson, Pálsson and Björnsson2014a). These uncertainties in DDF were not actually reported by Matthews and others (Reference Matthews, Hodgkins, Gudmundsson, Pálsson and Björnsson2014a), but are given here as ±0.65 and 1.39 mm w.e.°C−1 d−1 at VH 500 and VH 1100, respectively. Note that all reference to meteorological data and the SEB hereafter refers to the bias-corrected reanalysis and potential melt energy series, respectively. For clarity, we highlight that the 34 year potential melt record is referred to simply as ‘melt’ hereafter. Thus, note that the cross-validation procedure (described below) uses the modelled (potential) melt series as its reference.
To explain DDF variability through time, we analysed the role of the k individual energy fluxes in contributing to this behaviour, using (from Eqn (6)):
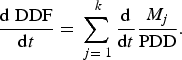 $$\displaystyle{{{\rm d}\;{\rm DDF}} \over {{\rm d}t}} = \mathop \sum \limits_{\,j = \; 1}^{\; k} \displaystyle{{\rm d} \over {{\rm d}t}}\displaystyle{{M_j} \over {{\rm PDD}}}.$$
$$\displaystyle{{{\rm d}\;{\rm DDF}} \over {{\rm d}t}} = \mathop \sum \limits_{\,j = \; 1}^{\; k} \displaystyle{{\rm d} \over {{\rm d}t}}\displaystyle{{M_j} \over {{\rm PDD}}}.$$
Hence, any trend in DDF with respect to time (T), can be attributed to individual trends in the fraction M j /PDD. To evaluate Eqn (7) we used regression: the slope term is a linear approximation of the derivatives.
The consequences of variability in DDF for melt simulations were assessed with a cross-validation procedure. Values for DDF were calibrated for each year in turn (using melt and PDD according to Eqn (2)) and the remainder of the melt series was then simulated using these DDF estimates and the respective PDD accumulated during each year. Errors in the cross validation were evaluated through comparison with the melt series for each location at annual resolution. Thus, DDF for both locations was calculated for 34 times, and for each iteration the remaining 33 years' melt was simulated and RMSE calculated. This procedure therefore quantifies the effects of variable DDF (resulting from changes in the prevailing weather only) on melt simulation error.
Where statistical significance is reported, we used a two-tailed t-test and a threshold p-value of 0.05 to indicate a ‘significant’ result. While the majority of the analysis presented here assesses DDF using melt and PDD accumulated at annual resolution, we also explore the daily SEB and temperature series to help shed light on the physical processes driving DDF variability (Section 4.3).
4. RESULTS
4.1. The SEB and DDFs
Figures 2 and 3 illustrate the meteorological and SEB series over the 1979–2012 period. Note that the SEB series displayed were also summarized by Matthews and others (Reference Matthews, Hodgkins, Gudmundsson, Pálsson and Björnsson2014a). The most significant trends for both locations were in air temperature and vapour pressure over the 1979–2012 period, which resulted in significant increases in the turbulent heat fluxes. Insolation displayed slightly weaker upward trends, which, because albedo is invariant, translated to similar increases in the net shortwave heat flux at both sites. Wind speed and incident longwave radiation remained essentially unchanged over the period assessed, and the latter is consistent with the lack of a trend in the net longwave heat flux at either location.

Fig. 2. The meteorological variables at the respective sites for the period 1979–2012. Best fit lines from a linear regression are plotted as solid lines, and the magnitude/significance of the respective slope parameters are indicated adjacent to the appropriate panel. Note that the colour of the text indicates which series (VH 500 = black; VH 1100 = grey) the slope parameters relate to.

Fig. 3. The SEB components at the respective sites for the period 1979–2012. The format of this figure is the same as Figure 2.
The DDF series for VH 500 and VH 1100 are illustrated in Figure 4. The mean of the 34 annual values for DDF is somewhat high at both locations (13.3 ± 0.49 and 14.5 ± 2.47 mm w.e.°C−1 d−1, at VH 500 and VH 1100 respectively, where uncertainty =±1 standard deviation (SD)) when compared with values reported in the literature (e.g. Braithwaite and Zhang, Reference Braithwaite and Zhang2000; Hock, Reference Hock2003), but these values are in reasonable agreement with those reported by Hodgkins and others (Reference Hodgkins, Carr, Pálsson, Guðmundsson and Björnsson2012), who derived DDF from AWS air temperatures and coincident measurements of surface elevation change detected by acoustic sounders during the summer of 2003 (mean DDF at 490 m = 11.8 ± 3.5 mm w.e.°C−1 d−1; mean DDF at 1100 m = 12.8 ± 4.5 mm w.e.°C−1 d−1, in which uncertainty ranges indicate ± 1 SD of daily values). Somewhat high mean DDF at VH 500 is perhaps unsurprising given the relatively low albedo found here (0.1), which reflects the presence of dirty ice due to wind-blown sand/dirt (Guðmundsson and others, Reference Guðmundsson, Björnsson, Pálsson and Haraldsson2009). While mean DDF at VH 1100 appears large, it should be noted that this reflects a melting snow/firn surface, and comparisons with existing studies are challenged by the fact that values of DDF are typically not reported along with snowpack state (dry/wet).

Fig. 4. (a) DDF evolution over the 1979–2012 period. Vertical bars indicate uncertainty as described in Section 3. The solid lines provide an 11 year, centred moving average to highlight low-frequency variability. End-points are smoothed with the maximum odd-length window possible. (b) Box plots of DDF. The notches indicate the respective medians, while the boxes span the interquartile range (IQR); the whiskers extend to the minimum/maximum values within 1.5 × IQR of the box limits.
4.2. Non-stationarity of DDFs
Examining DDF evolution through time, it is evident that interannual variability at VH 1100 is considerably greater than at the lower-elevation station. The SDs of the series in Figure 4 are 0.49 and 2.47 mm w.e. d−1°C−1 at VH 500 and VH 1100, respectively; hence, variability of DDF is more than five times greater at the higher-elevation site during this period. Close examination of Figure 4, does, however, indicate that DDF variance is decreasing at this location. The pronounced variability of DDF observed at VH 1100 means that factors calibrated on individual years do not transfer well for melt simulation in other years. Applying the cross-validation procedure resulted in RMSEs up to 70% of the mean annual melt at this location. This largest error was encountered when DDF from 1983 (22.51 mm w.e. d−1°C−1) was used to simulate melt in the remaining 33 years. Errors of this magnitude caution against transferring values of DDF between years at this location.
Trends in DDF during the period studied differ in magnitude between elevations. The trend at VH 500 (−0.86 ± 0.63% decade−1, in which uncertainty is the standard error of the slope coefficient when DDF is regressed with respect to year) is not significantly different from zero, whereas at VH 1100 a significant decline in DDF of −10.8 ± 2.3% decade−1 is apparent. This figure is in reasonable accord with the −7% decade−1 reported by Huss and others (Reference Huss, Funk and Ohmura2009). Contributions to the term dDDF/dt from the individual energy sources at VH 1100 are given in Table 2. It is evident that the largest contributor to the left-hand side of Eqn (7) is made by the net shortwave radiation, as the fraction M j /PDD decreased at a rate of −0.23 mm w.e. d−1°C−1 a−1 during the 34 year period studied. This decline more than offset the modest, positive contributions from the longwave and latent heat fluxes.
The reduction in DDF at VH 1100 is coincident with a rise in air temperatures at this location. Indeed, if DDF is plotted against PDD, a very clear relationship emerges (Fig. 5). It is this dependence on air temperature which explains the decline in DDF observed during the 34 year record. The cause of such behaviour can be explained by following Braithwaite (Reference Braithwaite1995), and writing melt as a linear function of PDD:
in which melt (M) contributed by the jth SEB component in year y is calculated by multiplying the factor of proportionality, β j , by PDD accumulated in the same year, with constant (α j ), and error term (ε jy ) added. From this, DDF for each year can be written (recalling Eqns (2) and (6)):
 $${\rm DDF}_y = \mathop \sum \limits_{\,j\; = \; 1}^{\; k} \beta _j + \displaystyle{{\alpha _j \;} \over {{\rm PDD}_y}} + \displaystyle{{\varepsilon _{\,jy}} \over {{\rm PDD}_y}}. $$
$${\rm DDF}_y = \mathop \sum \limits_{\,j\; = \; 1}^{\; k} \beta _j + \displaystyle{{\alpha _j \;} \over {{\rm PDD}_y}} + \displaystyle{{\varepsilon _{\,jy}} \over {{\rm PDD}_y}}. $$

Fig. 5. The relationship between DDF and PDD at VH 1100. The reference line is given by
![]() $\sum\nolimits_{j = 1}^k {\beta _j + (\alpha _j /{\rm PDDs}_y )} $
. Vertical error bars represent uncertainty in DDF, while horizontal error bars give uncertainty in PDD.
$\sum\nolimits_{j = 1}^k {\beta _j + (\alpha _j /{\rm PDDs}_y )} $
. Vertical error bars represent uncertainty in DDF, while horizontal error bars give uncertainty in PDD.
Assuming that the error has a conditional mean of zero, DDF can be approximated well with the last term on the right-hand side omitted from Eqn (9): it is this function which forms the reference line in Figure 5. Importantly, it then follows from Eqn (9) that if the sum of all α j is non-zero, DDF will be non-stationary with respect to PDD. The derivative is given by:
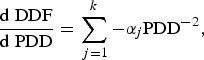 $$\displaystyle{{{\rm d}\;{\rm DDF}} \over {{\rm d}\;{\rm PDD}}} = \mathop \sum \limits_{\,j = 1}^k - \alpha _j {\rm PDD}^{ - 2}, $$
$$\displaystyle{{{\rm d}\;{\rm DDF}} \over {{\rm d}\;{\rm PDD}}} = \mathop \sum \limits_{\,j = 1}^k - \alpha _j {\rm PDD}^{ - 2}, $$
and the term d DDF/d PDD will approach zero asymptomatically as PDD increases.
Slope (β j ) and constant (α j ) terms were obtained for VH 500 and VH 1100 using linear regression (Table 3; Fig. 6). At both sites, the sum of all α j is positive, meaning that, according to Eqn (9), DDF should be expected to decline as PDD increases (because the term α j /PDD y becomes smaller). Equation (10) then indicates that the rate at which this decline occurs should be faster where air temperatures are lower (due to the term PDD−2). Importantly it is this relation that explains why the observed downward trend in DDF is much steeper at VH 1100. This location is appreciably cooler, and hence typically has much smaller PDD than VH 500 (less than one-third; Table 1). According to Eqn (10), this translates to a derivative of the DDF with respect to PDD more than 9 times larger than at VH 500, even if both locations were to have identical values of summed α j . It is therefore evident that the presence of non-zero α is of more importance for degree-day melt simulations in environments characterized by lower temperatures.

Fig. 6. Results from regressing the energy fluxes with respect to PDD at both elevations. The coefficients for the resulting lines are provided in Table 3. Vertical and horizontal bars indicate uncertainty estimates for the variables on the y- and x-axes, respectively. Abbreviations in the legend are: SHF, sensible heat flux; LHF, latent heat flux; LW, net longwave radiation; SW, net shortwave radiation.
Table 3. Results of regression performed on each of the energy fluxes with respect to PDD

β is the slope and α is the intercept. The values in brackets indicate the standard error of the regression coefficient and its associated p-value, respectively.
Physically, the α j terms represent the contribution to melting of the respective energy fluxes when PDDs are zero. Examining the individual values obtained for both VH 500 and VH 1100 yields results that are physically plausible. Only the net shortwave heat flux has intercept terms that are significantly greater than zero. The large, positive α j for net shortwave radiation is to be expected, as this flux is independent of air temperature. If this energy term is sufficient to offset the cooling of the temperature-dependent fluxes, melt may persist at 0°C (and below). Note that it is because α j is large for net shortwave radiation, that this energy flux contributes so heavily to the term d DDF/dt at VH 1100 (see Table 2; (10)).
4.3. Avoiding non-stationary DDFs
The analyses so far have demonstrated that DDF will only be stationary with respect to PDD if melting does not persist when PDD is zero. Where this condition is not satisfied, the sensitivity of melt to changes in air temperature (i.e. the β parameter) will be estimated wrongly if DDF is prescribed according to Eqn (2).
From the above, it follows that the undesirable non-stationarity of DDF may be corrected by adjusting the critical air temperature (T crit), beyond which melting occurs (i.e. the zero coordinate from which to calculate the PDD sum). A judicious choice would result in a zero α term and ensure DDF and β are equivalent. To explore the extent to which varying T crit improves the degree-day model at VH 1100 for simulating melt, the same cross-validation procedure described previously was employed. For this experiment, however, it was run repeatedly, and at each iteration, a different value of T crit was used to calculate PDD and DDF. Specifically, T crit was incremented in steps of 0.01°C over the range −5 to 1°C, and for every value of T crit, the average RMSE between simulated and observed melt for the 34 year series was calculated. A low error indicates stable DDF exhibiting little interannual variability.
Figures 7a and b demonstrate vividly the benefit of lowering the threshold air temperature at VH 1100. The optimum T crit is found to be −1.83°C. At this value, the average RMSE is reduced by ~70% relative to the usual choice of 0°C. For completeness, the results from applying the cross-validation procedure at VH 500 are also displayed in Figure 7b. DDF is considerably less sensitive to the choice of threshold air temperature employed at this location (due to the higher temperatures found here; Eqn (10)) but a slight reduction in simulation error is still recorded (average RMSE is reduced by ~12%) if T crit is adjusted to the optimum value (−1.03°C).

Fig. 7. (a) Comparison of RMSEs at VH 1100 when simulating melt with DDF calibrated using T crit values of 0°C and with the optimum value determined for this location, determined to be −1.83°C. Note that the RMSEs are overlain. (b) The results from repeatedly running the cross-validation procedure while varying T crit. Dotted lines in this panel highlight the mean respective errors when T crit = 0°C is applied. (c) The probability of daily melting for the respective air temperatures. The solid black line and shaded area respectively provide the median and ±1 SD across the 100 bootstrap realizations.
Temperatures below 0°C are very rare at VH 500 (occur on <1% of days), but more common at VH 1100 (occur on ~17% of days), which permits analysis of the SEB around the freezing point at this location, thus facilitating further exploration of the results shown in Figures 7a and b. We did this by examining the daily melt and temperature record to assess the probability of melting as a function of air temperature, which was pursued by using a sliding window, incremented in steps of 0.25°C, to assess the frequency of melting for air temperatures ±0.5°C of the window centre (Fig. 7c). To estimate the sampling distribution we conducted a bootstrap, by repeating the sliding-window analysis 100 times. For each realization 25% of the dataset was selected at random and the probabilities of melting were assessed. Evidently melting is common at 0°C (91.27 ± 2.53%; where uncertainty is 1 SD of melt probabilities calculated across the bootstrap realizations), but much less so at −1.83°C (11.75 ± 6.23%). Thus, at the optimum T crit determined from the cross-validation procedure, melting is indeed rare. This means that, when calculating PDD from this threshold, a regression of annual (JJA) melt upon concurrent PDD yields an intercept very close to zero (slope = 6.50 ± 0.32 mm w.e. a−1°C−1; intercept = 22.88 ± 95.48 mm w.e. a−1, in which uncertainty is given as the standard error of the fitted coefficients). PDD is also higher when this lower threshold air temperature is used, and these factors combined means that DDF is essentially stationary with respect to PDD (see Eqn (10)). To illustrate this point, we plot DDF at VH 1100 as a function of both time and PDD in Figure 8, which highlights the absence of any trends once T crit = −1.83°C is adopted. The mean DDF (6.58 ± 0.31 mm w.e. d−1°C−1) is now within 2% of the regression slope parameter.
Using the optimized values of T crit, the variability of DDF is reduced at both locations (Table 4). This change is relatively modest at VH 500, where the coefficient of variation (cv) decreases by ~11%, but DDF was already relatively stable over the 34 year period at this location (Section 4.2). At VH 1100 the reduction is more prominent, as cv is reduced by ~78%. In Table 4, we also show the sensitivities of DDF to the different energy-balance components calculated from linear regression. At VH 500 sensitivities are somewhat low, irrespective of the value of T crit adopted. The maximum absolute sensitivity found here is to the longwave heat flux (−2.39 ± 0.48% σ −1, where σ denotes SD). Sensitivities at VH 1100 are much higher when T crit = 0°C is applied, with the largest absolute value witnessed for the sensible heat flux (−25.00 ± 3.14% σ −1), but all sensitivities reduce considerably when the lower value of T crit is employed. The greatest sensitivity for T crit = −1.83°C is exhibited with respect to the latent heat flux (5.44 ± 1.57% σ −1). When the optimum threshold air temperature is applied, DDF at both locations is clearly rather stable with respect to changes in the SEB over the 34 year period investigated.
Table 4. Summary of DDF and SEB sensitivities before and after adjustment to the optimum T crit. cv is the coefficient of variation (SD divided by the mean – multiplied by 100 for display), while the sensitivities to the SEB components, calculated as slope coefficients from linear regression, are reported as % per SD change in melt contribution from the respective SEB component

‘Rad.’ and ‘turb.’ denote the radiative and turbulent SEB components, respectively, while ‘temp. dep.’ refers to the temperature-dependent heat fluxes (turbulent and longwave heat fluxes).
5. DISCUSSION
There are two particularly important points emerging from this research. The first of these is that the threshold air temperature is of significant importance for degree-day melt simulations, particularly at lower air temperatures. Incorrect specification of T crit results in non-stationary DDF as air temperature changes, and melt simulations may be compromised as a result. Braithwaite (Reference Braithwaite1995) observed similar results from modelling investigations in western Greenland, noting that high DDF was possible with low air temperatures if melting persisted at 0°C. This study also outlined the possibility that such high DDF was likely to decrease as air temperatures increased. Hence, the analyses presented here have supported this insight experimentally.
While it is generally assumed that the onset of melt occurs at 0°C (Hock, Reference Hock2003), consideration of the SEB and the typical meteorological conditions encountered on glaciers suggests that melting may actually be possible over a wide range of air temperatures (Kuhn, Reference Kuhn1987; Braithwaite, Reference Braithwaite1995). Our finding of subzero T crit is supported by both van den Broeke and others (Reference van den Broeke, Bus, Ettema and Smeets2010) and Senese and others (Reference Senese, Maugeri, Vuillermoz, Smiraglia and Diolaiuti2014), who report threshold daily mean air temperatures of ~−5°C at the onset of melting. However, we emphasize that different values of T crit should be expected between locations, as this parameter is determined by the respective microclimate.
The importance of the local climate conditions in determining the temperature at which melting initiates is highlighted if careful consideration is given to the surface energy fluxes around the melting point. At the onset of melting, Q = 0 W m−2 and the glacier surface is at 0°C (Kuhn, Reference Kuhn1987). Hence, to find T crit is to find the air temperature, T, which satisfies this condition. For subzero T crit, the only component that can act as an energy source is the shortwave heat flux. Ignoring energy transferred by rain, and assuming no ground heat flux and constant atmospheric pressure, the SEB at the onset of melting can be written as a function of the relevant meteorological variables:
where Ws is the wind speed, RH is relative humidity, and ε is the atmosphere's thermal emissivity. The remaining symbols retain their meaning from Eqn (3). A detailed review of the form of the relations summarized in Eqn (11) can be found in Hock (Reference Hock2005); the purpose of its inclusion here is to highlight qualitatively the role of the different meteorological variables in determining T crit. For constant wind speed (Ws), humidity (RH) and thermal emissivity (ε), the value of T required to satisfy Eqn (11) decreases as Q SW increases; for fixed Q SW, lower T is required if RH and ε are higher, and if Ws is lower. It is therefore evident that variability of T crit should indeed be anticipated, even across a single glacier, as changes in Q SW (which itself depends on the incident shortwave flux and albedo), Ws, RH and ε will alter the temperature at which Eqn (11) is satisfied.
While the decision to neglect the ground heat flux (Q G) in Eqn (11) has some support for temperature Icelandic glaciers (Flowers and others, Reference Flowers, Marshall, Björnsson and Clarke2005), others have highlighted the potential importance of this flux, particularly for snow-covered sites that experience ablation season temperatures close to the melting point (Greuell and Oerlemans, Reference Greuell and Oerlemans1986; Pellicciotti and others, Reference Pellicciotti, Carenzo, Helbing, Rimkus and Burlando2009). Including Q G in Eqn (11) would act to raise T crit if all other terms were kept constant, as higher temperature-dependent heat fluxes would be required to offset any energy lost via conductive heat flow to the subsurface. Because we omitted Q G in our SEB simulation, it is possible that we obtained optimized values of T crit that are on the low side. This is perhaps more likely at VH 1100, which is colder and snow-covered (hence more likely to experience non-zero Q G). Our results may therefore provide a pessimistic view of the discrepancy between the appropriate values of T crit determined for our study sites, and the 0°C often assumed.
It follows from the above that a constant T crit is implausible in both space and time, which is perhaps problematic given the importance of this parameter noted in our study. In this regard, though, determining average values based on climatological considerations of the meteorological variables given in Eqn (11), may provide a solution that is more appealing than the usual zero-degree assumption encountered in degree-day melt modelling. While the development of such an approach is beyond the scope of this study, we note that techniques such as the coupling of remote sensing methods used to detect melt occurrence (e.g. Mote and others, Reference Mote, Anderson, Kuivinen and Rowe1993) with gridded climate data products (e.g. Dee and others, Reference Dee2011), may yield insight in this respect.
The second important point raised by this research is the stationarity of DDF once T crit had been adjusted appropriately. That is, despite the fact that air temperatures have changed appreciably during the 34 year period studied, the ratio between melt totals and air temperature remained approximately constant, and we detected a very low sensitivity of DDF to changes in the SEB. This is interesting because it is inconsistent with the results reported from the Swiss Alps by Huss and others (Reference Huss, Funk and Ohmura2009) who cautioned against applying values of DDF beyond their calibration period, due to a marked decline in DDF since the mid-1970s. The downward trend was observed to be coincident with rising air temperatures, and as a consequence it was cautioned that degree-day melt models may be unsuitable for projecting melt in a changing climate. Without insight into the SEB, Huss and others (Reference Huss, Funk and Ohmura2009) were not able to diagnose the cause of this non-stationarity. However, we suggest here that as the authors prescribed T crit to be 0°C, it is possible that an incorrect specification of the threshold air temperature may explain the downward DDF trend; this would be consistent with the results from VH 1100.
Our results indicate temporal transferability of DDF values in the context of a changing climate, supporting studies that have utilized this assumption for Icelandic mass-balance modelling in particular (Flowers and others, Reference Flowers, Marshall, Björnsson and Clarke2005, Reference Flowers2008). However, the experimental framework our results are based on does not consider some important feedback processes in the SEB and our findings are site-specific. This may also contribute to the discrepancy between the results reported here and those of Huss and others (Reference Huss, Funk and Ohmura2009). The 34 year SEB series we analysed was produced under the constraint of constant surface conditions (hypsometry, roughness and albedo: Section 3; Matthews and others (Reference Matthews, Hodgkins, Gudmundsson, Pálsson and Björnsson2014a)). In reality, however, the glacier surface state is dynamic and in fact influenced by the SEB. For example, cumulative melting has been shown to increase surface roughness lengths and decrease surface albedo (Brock and others, Reference Brock, Willis and Sharp2000, Reference Brock, Willis and Sharp2006). The latter process can be expected to increase the ratio between melt and PDD, and hence increase the DDF, while the former is likely to contribute in the same manner, depending on the sign and magnitude of the near-surface vapour pressure gradient. The possible impact of dynamic hypsometry on DDF is more challenging to estimate. Such changes have the potential to influence the local microclimate (and hence the SEB) in multiple ways: for example as glaciers retreat, insolation could be affected by changing shading patterns, while the thermodynamic properties of glacier boundary layers may change as the surface elevation is reduced and the cooling effect of glaciers is diminished (cf. Shea and Moore, Reference Shea and Moore2010). In neglecting these sources of complexity, we provide a simplified view of DDF variability over the period 1979–2012, which only considers the influence of changes in the prevailing weather in driving SEB variability.
It should also be noted that our reconstruction of potential melt energy assumes that the bias correction applied to the reanalysis data remains suitable for the duration of the hindcast, but this assumption cannot be verified. Matthews and others (Reference Matthews, Hodgkins, Gudmundsson, Pálsson and Björnsson2014a) did however find that very little of the reanalysis data in the hindcast period lay beyond the bounds of the data used to calibrate the quantile-mapping adjustment they applied, which adds confidence to the bias correction. Moreover, as we use the ERA-Interim reanalysis – which only covers the recent observation-rich data period (1979 onward, Dee and others, Reference Dee2011) – the quality of this dataset (in terms of representing the synoptic circulation) is likely to be high throughout the simulation period. Thus, we conclude that this source of uncertainty in our reconstructions of potential melt energy is likely to be small.
In summary, we highlight that our experimental framework does provide a simplified view of DDF variability. However, the physically consistent approach to the analysis has permitted a more-detailed view of interdecadal variability in this parameter variability than has been offered to date. This insight suggests that DDF at our study sites is relatively insensitive to the recent variations in potential melt energy that accompanied climate change.
6. CONCLUSIONS
A critical assumption invoked when applying the degree-day model to simulate interannual variability in melt is that DDF remains constant in time. Because records of the SEB or indeed contemporaneous measurements of surface melt and air temperature are seldom available over suitably long periods of time, it is often problematic to falsify this assumption experimentally. In this study, we have made a contribution in this regard by examining DDF variability over a 34 year period characterized by a changing climate.
We observed a significant downward trend of this model parameter at VH 1100, but this was found to be spurious and could be attributed to an incorrect specification of the air temperature from which to initialize the positive-degree-day sum (T crit). Our results highlight that an inappropriate choice of this parameter has a larger effect on the non-stationarity of DDF in environments characterized by lower air temperatures, and it is for this reason that substantial errors in simulated melt were noted in a cross-validated melt simulation at VH 1100.
The spurious trend that we attributed to misspecification of T crit is also troubling for studies that seek to investigate the validity of the assumption that DDF remains constant as the climate changes. Unless the role of T crit is addressed explicitly, we conclude that misspecification of this parameter cannot be ruled out as an alternative explanation for apparent violations of this assumption. Indeed, once T crit had been adjusted appropriately, we observed no trend in DDF at our locations during a 34 year period characterized by climate warming.
Given the importance of T crit observed in this work, it is recommended that future research should attempt to constrain this parameter explicitly. Integrating such an approach into long-term studies of DDF variability on other glaciers worldwide will be an important contribution in further understanding the extent to which the assumption of constant DDF is valid in a changing climate.
ACKNOWLEDGEMENTS
We acknowledge S. Guðmundsson, F. Pálsson and H. Björnsson (Institute of Earth Sciences, Reykjavik) for the use of AWS data from Vestari Hagafellsjökull. We also thank two anonymous reviewers whose comments improved this work substantially.















