Introduction
The West Antarctic ice sheet (WAIS) contains 11 major ice streams moving at speeds 10–100 times faster than the surrounding ice, with the exception of the lower part of Kamb Ice Stream (former Ice Stream C) that slowed considerably about 150 years ago (Reference Retzlaff and BentleyRetzlaff and Bentley, 1993). These are speeds much higher than can be explained by internal deformation of the ice alone. Additional mechanisms, like basal sliding and basal bed deformation, have to contribute in order to account for the remarkable dynamics of these ice currents. For these mechanisms to become active, the base of the ice streams has to be at the pressure-melting point and well lubricated by water at high pressure. The contribution from sliding can be substantial, sometimes close to 100% of total speed (Reference Engelhardt and KambEngelhardt and Kamb, 1998). The causes for melting or freezing conditions at the base are: (a) the climate history at the surface, namely temperature and snow accumulation; (b) the thermal and flow history of the ice, namely internal and basal frictional heating, heat conduction and heat advection; and (c) the geothermal flux.
The purpose of this work is to present measurements of the temperature profiles in the ice at Siple Dome (SD), especially the basal temperature gradient that reflects the geothermal flux. The latter can be measured unequivocally only at a place where the ice was frozen to the bed for a long time, so that the freezing front has penetrated deep into bedrock and sources of latent heat from water are absent. The best location for such measurements on the WAIS is at the summit of SD (81.658° S, 148.809° W; 601 m a.s.l.) (Fig. 1). SD is the largest interstream ridge, located between Kamb Ice Stream and Bindschadler Ice Stream (former Ice Stream D). The ice at SD is moving very slowly, by internal deformation, of the order of 0–10 m a-1. Precisely at the summit, the horizontal speed is zero because the surface slope and therefore the driving stress is zero. Although the exact location of the summit may have shifted with time due to changing accumulation patterns, it is assumed that the central part of SD has existed in the same vicinity since the last ice age or longer (Reference Nereson, Raymond, Waddington and JacobelNereson and others, 1998).

Fig. 1. Five major West Antarctic ice streams flow from the WAIS into the Ross Ice Shelf. SD is part of an interstream ridge between Kamb Ice Stream (C) and Bindschadler Ice Stream (D). Mercer Ice Stream (A), Whillans Ice Stream (B), and MacAyeal Ice Stream (E) also belong to the WAIS system. The dots indicate borehole locations.
The absence of, or very low, velocity at or near the summit of SD removes shear heating, heat advection and basal friction as sources in the heat-balance equation, providing a much simplified case of the general heat-flow problem, and also making interpretation less complicated. Previous measurements of temperature profiles from the WAIS surface to the bed were made at Byrd Station and at Whillans Ice Stream (Reference Gow, Ueda and GarfieldGow and others, 1968; Reference Engelhardt and KambEngelhardt and Kamb, 1993). Other temperature measurements were taken on the Ross Ice Shelf at drill siteJ9 (Reference MacAyeal and ThomasMacAyeal and Thomas, 1979) and Crary Ice Rise (Reference Bindschadler, Roberts and IkenBindschadler and others, 1990). However, in most boreholes, the bottom temperature is fixed at the pressure-melting point. In these cases, the water available at the bed or in the till provides sources of latent heat. The ice is flowing and produces shear heating within the ice and at the base. So many heat sources in addition to the geothermal flux make the separation of the geothermal contribution impossible. In contrast, SD is frozen to its base so that the same heat flux in the rock beneath the ice can flow through the ice–rock interface into the ice. Extensive modeling has been done to elucidate the influence of the geothermal flux on the non-steady-state temperature profiles in ice sheets (Reference Robin and deRobin, 1955, 1976; Reference Jenssen and RadokJenssen and Radok, 1961; Reference LliboutryLliboutry, 1963; Reference MüllerMüller, 1963; Reference WeertmanWeertman, 1968; Reference Budd, Young and AustinBudd and others, 1976; Reference Paterson and ClarkePaterson and Clarke, 1978; Reference Dahl-Jensen and JohnsenDahl-Jensen and Johnsen, 1986; Reference RitzRitz, 1987,1989; Reference WaddingtonWaddington, 1987; Reference PatersonPaterson, 1994).
Measurements
To measure the vertical temperature profile through the ice at the summit of SD during the 1997/98 field season, we drilled two boreholes specifically for this purpose, one to the bed at 1004.6 m depth, and a shallow one to 120 m depth, using the Caltech hot-water drilling system that allows completion of a 1000 m deep, 10 cm diameter borehole in 16 hours. Forty additional boreholes were drilled for the measurement of vertical strain rates (Reference ZumbergeZumberge and others, 2002).
During and after drilling, meltwater from the drilling was standing in the boreholes up to a depth of about 27 m below the surface, which is the depth of the base of the permeable firn layer. As the ice-sheet bed was reached, the hot-water drill came to a sudden stop, normally indicating a hard rock bed. A subsequent attempt to obtain a soil sample from beneath the bed using a piston corer produced a very small amount of debris but also a smashed cutting head, again showing the hard rock bottom of the borehole. Had the ice been underlain by a layer of glacial rock debris (till) or debris-laden ice as is the case in most boreholes drilled to the base of the ice streams, the hot-water drilling jet would have melted and hydraulically mined through it for several meters, and the piston corer would have picked up a good sample of debris. Also, in ice streams, when the bottom of the ice is reached and the drill encounters a wet bed with a hydraulic system at a water pressure close to the ice overburden pressure, the water level in a 1000 m borehole would drop from 27 m to about 100 m below the surface. Other boreholes reaching the bed in the vicinity of SD did not encounter a soft water-saturated bed either, which is a good indication that at SD the ice sheet is solidly frozen to a rock bed. Such observations allow one to ascertain, before making any temperature measurements, that water sources that could contribute latent heat are not present at or near the ice–bed interface at SD.
To measure borehole temperatures, we use thermistors with temperature-dependent resistances of nominal 5 kΩ at 25°C, which were carefully calibrated to ±0.02°C for the expected temperature range, using an ice bath and certified precision thermometers. The measured thermistor resistances vs temperatures were least-squares fitted to the Stein- hart thermistor equation. Several thermistors recalibrated 2 years later showed no drift. The thermistors are enclosed in pressure-tight tubings closed off with soldered glass metal electrical feed-throughs. This was necessary to protect the thermistors from being crushed by transient very high pressure during borehole freeze-in and also to avoid possible changes in response to high ice-overburden pressure. The transient pressure increase depends on the freeze- in rate. We tried to measure the additional pressure, but it exceeded our limit of 27 bar. Previously, we also used unprotected thermistors, but the failure rate was high and unpredictable, while the sealed thermistors survived at least 4 years frozen in the ice at all depths. The thermistors were connected to individual wires of different length bundled together to form thermistor strings. Malfunction of one thermistor would not compromise the whole string.
The thermistor strings were deployed into the water- filled borehole immediately after completion of drilling. Complete freeze-in occurred in <1 day in the upper cold part of the borehole. The thermistor 25 m above the bottom needed 10 days, and the bottom thermistor was not frozen at the end of the season 2 months later. Thermistor resistances were recorded on a data logger daily, and again 1 and 2 years later in November 1998 and 1999 when the drill site was revisited. It takes a long time, especially near the bed, for the temperature disturbance introduced by hot-water drilling to dissipate. The resistance measurements of frozen-in thermistors can be carried on for several years until the temperature has nearly equilibrated with the environment. Temperature measurements in mechanically drilled boreholes filled with drilling fluids other than water are more difficult because the increasing temperature with depth can cause convective cell mixing and because of the long time required to get the sensor in equilibrium with the surrounding ice temperature, especially when a precision of 0.02°C is required. The effect of temperature distortion is especially severe in air-filled shallow boreholes or in crevassed areas where cold-water air pools at the bottom and stays there. Temperatures measured in crevasses were up to 12 K lower than in the uncrevassed ice (Reference Alley and BentleyAlley and Bentley, 1988; Reference Harrison, Echelmeyer and LarsenHarrison and others, 1998).
Temperature Profiles and Geothermal Flux
Final ice temperatures are obtained by plotting temperature vs inverse time and linearly extrapolating to the temperature at inverse time equal to zero (infinite time) (Reference Engelhardt and KambEngelhardt and Kamb, 1993). Most temperatures reached after 2 years come to within a few hundredths of a degree of the extrapolated final value, except the bottom temperature, that needed an extrapolation of-0.2°C.
The observed temperatures are tabulated in Table 1 and plotted in Figure 2. The bottom temperature is -2.54°C, well below the pressure-melting point for clean ice at -0.7°C.
Table 1. Observed temperatures at discrete heights above bottom of the Siple Dome ice sheet


Fig. 2. Observed and calculated temperature profiles. Steady-state profile for present climatic conditions at right, and for ice-age conditions at left. Transient temperature profiles from left to right in two 1kyr steps and eight 2 kyr steps after a temperature jump at the surface. Observed temperatures lie on the 10 kyr profile.
The basal temperature gradient of-32°C km-1 could be converted into a heat flux in the ice of 70.4 mW m-2 using a thermal conductivity of 2.2 W m-1 K-1 near 0°C. In the following we want to evaluate how closely this heat flux reflects the geothermal flux.
To elucidate the thermal state of the ice sheet evolving over time, both steady-state and transient calculations were performed. The temperature profile at SD was calculated using a coupled heat- and ice-flow equation that was simplified by the absent horizontal advection and shear heating (Reference PatersonPaterson, 1994).

where T is the temperature, t the time, k the thermal diffusivity (1.1 × 10-6 m2s-1), z the vertical coordinate, vz the vertical flow velocity of the ice, f the heat from internal deformation, ρ the density of ice and c the heat capacity of ice. k and c vary with temperature according to the parameterization given by Reference PatersonPaterson (1994). According to Reference Paterson and ClarkePaterson and Clarke (1978) and Reference WaddingtonWaddington (1987), the influence of the internal deformation from the vertical compression is minimal. Its influence on the basal temperature is about 0.1°C. We therefore follow the usual practice and drop the last term in our calculations. Instead of a normally assumed linear dependency of vz on z, we use a more appropriate dependence derived by Reference RaymondRaymond (1983) for the special case of an ice divide like SD summit. This choice is suggested by the shape of the internal layering of radar reflectors, which shows a peculiar bump in the vicinity of the dome.

where a is the accumulation rate and h is the ice thickness. This type of relationship is confirmed by direct measurements (Reference ZumbergeZumberge and others, 2002). The steady-state temperature profile (∂T/∂t = 0) is given by

where
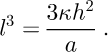
The subscript s designates surface, and b stands for basal values. The averaged mean annual surface temperature is -24.9°C as measured 20 m below the surface, and the temperature actually measured at the surface, averaged over 2 years from 1997 to 1999, was -24.4°C. The recent accumulation rate is 0.1 ma-1 (Reference Nereson, Raymond, Jacobel and WaddingtonNereson and others, 2000). First, we tried to fit our borehole temperature measurements to the steady-state equation. This could only be done with an unrealistic accumulation rate of twice the present value. A linear dependence of vz on z would give a better fit, but is not satisfactory for the reasons Reference RaymondRaymond (1983) presented. This led to the conclusion that the temperature distribution in the ice is not in steady state, because surface temperature and accumulation changes in the past may not have allowed the temperature to equilibrate fully. In fact the profile will never reach complete equilibrium since climate will keep changing and the ice sheet has such a long-term memory. Daily variations, seasonal changes and annual fluctuations in surface temperature average out fairly quickly in the ice with depth. Usually the ice temperature at 20 m below the surface is taken as the mean annual surface temperature averaged over decades. Any temperature trend over this short time period is ignored in our calculation. Millennial temperature changes reach much deeper into the ice. They are responsible for the variations in the upper 200 m in the temperature-depth profile. Using the time-dependent heat- transport equation from above and applying a finite-differencing scheme, a sequence of temperature profiles is calculated. The time sequence starts by calculating an initial steady-state temperature profile reaching 4 km into bedrock by using boundary conditions representing the last ice age when, on average, temperatures were about 10 K lower and the accumulation rate was about 0.05 m a-1, half the present value. This profile is shown in Figure 2 as the leftmost in the family of profiles. At 10 000 years (10 kyr) ago, we let the surface temperature and the accumulation rate jump to the present-day values. The time for the change to take place is short compared to the overall model time, 10 kyr for an ice sheet of 1000 m thickness. The observation of melt layers in ice cores extracted from our boreholes at SD indicates that high temperatures were already reached at least 10 kyr ago. This is confirmed by the work of Reference DasDas (2003) who showed that melt layers started to appear about 11 kyr ago after the end of the last ice age.
It is also assumed in our calculations that the ice thickness did not change, because colder temperatures and lower accumulation rate have opposite effect on ice thickness. If the ice were 100 m thicker, the temperature at the base would increase by about 1°C. The temperature profiles evolve over time as shown in Figure 2. After 7000 years, half of the temperature jump at the surface has propagated to the bed. The temperature profiles in the sequence are 2 kyr apart, except the first two time-steps are 1 kyr. It takes about 16 kyr for the basal temperature to reach the melting point. The last profile at right is again a steady-state calculation with the bottom temperature fixed at the melting point of -0.7°C. In all of the transient calculations, we choose a constant geothermal flux deep in the earth of 69 mW m-2. From the sequence of temperature profiles, the one obtained 10 kyr after the initial jump in surface conditions fits best the presently measured profile, at least in the lower half of the borehole. The basal temperature gradients vary from initially -31.4 to -32.0 Kkm-1, corresponding to the present situation, to -32.17 K km-1 in the future when the bed reaches melting temperature. The temperature profiles are almost linear and almost parallel at great depths because they are controlled by conduction of the geothermal flux. They are curved at shallow depths because they are strongly influenced by surface accumulation. If we converted the present basal temperature gradient directly into a geothermal flux, we would obtain -70.4 mWK-1, thus making an error of about 1mWK-1. To explain the upper part of the borehole in detail would require a much more realistic surface condition history that is not very well known. Additional temperature-profile calculations show that a surface temperature jump even larger than 10 K or one occurring more gradually and a slightly thicker ice sheet during the last ice age keeps the uncertainty within about 1 mW K-1.
Discussion
The geothermal flux of 69±1mW m-2 at SD is significantly higher than the typical flux for old stable continental crust, 17–31 mW m-2 (Reference Sclater, Jaupart and GalsonSclater and others, 1980), and also much higher than the flux found for Greenland, 51.3 mW m-2 (Reference Dahl-JensenDahl-Jensen and others, 1998), except for a local caldera structure under a large ice stream in northeast Greenland (Reference Fahnestock, Abdalati, Joughin, Brozena and GogineniFahnestock and others, 2001), or the average flux estimated for Antarctica of 54 mW m-2 (Reference Sclater, Jaupart and GalsonSclater and others, 1980). More recent work by Reference Shapiro and RitzwollerShapiro and Ritzwoller (2004) uses a global seismic model and the structural similarity of crust and upper mantle to create a heat-flow map of Antarctica. They show that the WAIS has a heat flow three times higher than that of East Antarctica. For a point in West Antarctica (78° S, 110° W) they calculate an average heat flow of 110 mW m-2 with a standard deviation of 60 mW m-2.
This result suggests that the WAIS is based on relatively young crust, which is in agreement with the fact that West Antarctica is a rift system with volcanism (Reference Blankenship, Bell, Hodge, Brozena, Behrendt and FinnBlankenship and others, 1993; Reference BehrendtBehrendt and others, 1996, 1998). In a rift system with blocks of crust or sediments of varying thickness, the geothermal flux is normally not only higher but also more variable. In West Antarctica it is likely that in some areas, especially near volcanos, much higher fluxes than measured at SD are possible. Our precise measurement of the geothermal flux at one point is probably only representative of the SD area and its adjacent ice streams (Reference Gades, Raymond, Conway and JacobelGades and others, 2000), but it fits well into the global picture envisioned by Reference Shapiro and RitzwollerShapiro and Ritzwoller (2004).
The elevated geothermal flux probably is the root cause for the dynamics of the WAIS by making it easier to bring the basal ice up to the melting point, without which the great number of active and now relatively shallow ice streams, as compared to East Antarctica, would not have started in the first place.
From our transient temperature calculations it also becomes clear that not only is geothermal flux important for the present basal conditions, but also global warming, which took place after the last ice age 10 kyr ago, influences the basal temperatures thousands of years later at present. A drastic temperature change at the surface is barely felt 1000 years later at the bottom of a 1000 m deep ice sheet. During the last 10 kyr the surface temperature rose from an ice-age value to the present-day temperature. This translates into an equivalent rise in bottom temperature with a delay of thousands of years. Today’s temperatures at the bed of the WAIS, which are at or close to the melting point, are the result of postglacial temperature increases. They are the highest in the last 10 kyr and still rising. The surface temperature may have been temporarily a few degrees higher during the last climatic optimum 8–5 kyr ago, but this effect was too small to be felt at the bottom.
More recent temperature changes like the warm period around 1000 BP, followed by the Little Ice Age from 1550 to 1850 and the warming trend during the last 100 years especially in the 1930s and 1990s, show up as temperature variations in the upper part of the temperature profile. However, the density of data points in the upper part is not high enough to allow a precise quantitative reconstruction. They are real because they show up in a number of boreholes. They have no immediate and direct impact on the bottom temperatures. Indirect consequences of further global warming, however, can be quite significant. Breakup of the large floating ice shelves, especially the Ross and Ronne Ice Shelves, will be accelerated in a warming climate by meltwater filling crevasses on the ice shelves and in the shear margins of the ice streams, and by increasing basal melting from warmer ocean currents reaching under the ice shelves. Some ice streams formerly protected by the ice shelves are thinning, speeding up and disintegrating at an accelerated rate similar to the large tidewater glaciers in Alaska, U.S.A., that have catastrophically receded during recent decades (Reference MeierMeier and others, 1994; Reference RignotRignot, 2002; Reference RignotRignot and others, 2002). The recent break-up of the Larsen Ice Shelf, the calving of immense icebergs from West Antarctic ice shelves and also the ominous shrinking of the seasonal sea-ice cover may be more than regularly recurring episodes, and could be indicators of more dramatic changes ahead. The break-up of the floating ice shelves would not contribute to a rise in sea level per se, but a later consequence could be a speed-up of the ice streams and the disintegration of the entire WAIS, which would increase sea level by about 6 m.
The fact that the base of SD will reach the melting point indicates that it probably melted at the base during the last warm age about 120 000 years ago. Extensive melting at that time may have removed older ice, which agrees with the fact that we find no debris in the lowest ice core at SD. In that case, the oldest ice at SD is not older than about 120 000 years. The same argument may also apply to other places in West Antarctica. Reference Scherer, Aldahan, Tulaczyk, Possnert, Engelhardt and KambScherer and others (1998) argue that most of the WAIS must have been open ocean during the late Pleistocene, because of the age of the diatoms found in till samples collected at WAIS borehole sites.
The geothermal flux determined at SD near fast-moving ice streams in the lower reaches of the WAIS may be different elsewhere. A few hundred kilometers further upstream in the catchment areas of the ice streams, subglacial volcanos have been located by aerogeophysical surveys (Reference BehrendtBehrendt and others, 1996, 1998). It would be reasonable to assume much higher basal geothermal fluxes in the vicinity of volcanos than under SD. They may have produced subglacial water reservoirs where ice-stream surges could have been triggered, similar to glacier surges where water-pressure lubrication plays the decisive role (Reference KambKamb and others, 1985). They may continue to provide lubrication water for the active ice streams with very high basal sliding speeds. Basal friction is not strong enough to resist the driving stresses. Friction at the shear margins and, at several bedrock humps, sticky spots within the ice streams make up the difference (Reference RaymondRaymond, 1996). At present, the interstream ridges like SD, still frozen at the bed, provide the major resistive forces. The temperature increase with time for the base of SD from the transient calculations is given in Figure 3. The pressure-melting point would be reached in about 6000 years from present. SD and likewise other interstream ridges would be lubricated by meltwater and would start to slide. The ice-stream shear margins, already weakened by shear heating and surface meltwater penetration in a warmer climate, would lose their grip on the ice streams. This would be the long-term scenario for the WAIS to disintegrate as it did in the past (Reference Scherer, Aldahan, Tulaczyk, Possnert, Engelhardt and KambScherer and others, 1998), but the experience of the last 10–20 years is that things can surprisingly happen much faster. More borehole drilling and ongoing full three-dimensional modeling of the dynamics of the WAIS will reveal interesting details about its future evolution, especially when constrained by borehole measurements of temperature profiles and a better understanding of basal conditions (Reference Hulbe, Payne, Alley and BindschadlerHulbe and others, 2001; Reference Tulaczyk, Kamb and EngelhardtTulaczyk and others, 2001; Reference Joughin, Tulaczyk and EngelhardtJoughin and others, 2003).

Fig. 3. Bottom temperature for a 1000 m deep ice sheet with time in kyr after a 10 K temperature jump at the surface, using a deep geothermal flux that fits best the present observed basal temperature gradient.
Acknowledgements
I wish to thank B. Kamb for his invaluable support that made this work possible. I admire the incredible perseverance of our field assistants R. Bolsey, A. Blanchard, D. Reusch, A. Bucki, S. Colley, B. Farrow, E. Mueller and H. Schwaiger who participated in the Siple Dome hot-water drilling project. This work was supported by a grant from the U.S. National Science Foundation Office of Polar Programs. Antarctic Support Associates and the U.S. Navy provided logistics support.






