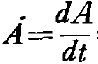Introduction
Previous discussion of this subject by Brockamp Reference Brockamp 1 , Reference Brockamp 2 has considered the effect of the outflow of heat from the Earth, and of internal friction on the temperature of the ice sheet. The effect of accumulation in modifying the winter “cold wave” in a snowfield has been considered in detail by Benfield.Reference Benfield 3 A large accumulation was shown to affect the form of the cold wave appreciably, but the effect with a small accumulation was not significant.
The object of this paper is to show for a polar ice sheet (that is one where the layers of ice or firn near the surface remain below freezing point throughout the year) that even a small accumulation will produce a considerable effect on the temperature gradient in the ice. A quantitative expression for the variation of this gradient with accumulation, ice thickness and depth has been derived which should be applicable near the centre of a stable ice sheet. Under certain circumstances, which probably apply in the southern half of the Greenland Ice Cap, it is shown that a negative temperature gradient (i.e. temperature decreasing downwards) may be formed as a stable feature.
Theory
It is necessary to make certain assumptions regarding an ice sheet as a starting point from which to tackle this problem. We consider only the case of a stable ice sheet, that is one which is of constant size, and in which the temperature distribution does not vary with time. We will regard the ice sheet as having a two-dimensional form of a type outlined by Nye.Reference Nye 4 Fig. 1 (p. 525) shows a cross-section of such an ice sheet, and serves to explain the various symbols.

Fig. 1. Symbols used in discussion of an ice sheet
At the centre of the ice sheet H is the total thickness and h the height above the base of the ice sheet, H′ and h′ are the corresponding quantities at distance r from the centre, R being the half width. Other symbols used are:
-
θ = temperature
-
t = time
-
q = rate of outflow of geothermal heat per unit area
-
K = thermal conductivity of ice (5.3 × 10−3 cal./cm./sec./degree C.)
-
k = thermal diffiusivity of ice (1.18 × 10−2 cm.2/sec.)
-
= rate of accumulation of ice on upper surface of ice sheet. This is assumed constant over the ice sheet.

The upper surface of the ice sheet is assumed to fit the equation Reference Nye 4
where h 0 is a constant.
The rate of outward movement of a column distant r from the centre is

We also assume that any vertical column remains vertical in spite of movement over the sub-glacial floor. We consider that the effect of accumulation, or of decreasing thickness due to outward movement, increases the cross-section of a vertical column uniformly at all depths. Thus at the centre of the ice sheet, if we neglect effects of compression, which are only significant close to the surface, the rate of vertical movement of the ice at any level h due to surface accumulation is given by

The above mechanism approximately fits that proposed by Nye Reference Nye 4 and some such simplified picture is necessary to facilitate analysis. Alternative mechanisms can be used which require modification of (3), as is done in the case of ice shelves later.
Temperature Gradient at the Centre of an Ice Sheet
Consider a vertical prism near the centre of an ice sheet. The general equation of heat flow is

We will consider the horizontal temperature gradient in the ice sheet as negligible, as in the case of central Greenland, its mean value cannot exceed 1° C. per 10 km. We can then simplify (4) to

By substituting (3) in (5) and integrating we can obtain a solution for the temperature gradient at any level as

e being the exponential function and


Tables (1) and (2) show how these temperature gradients vary near the centre of two ice sheets, of thickness 3000 m. and 400 m. respectively.
Table I Central Thickness of Ice Sheet (H) 3000 m.

Table II Central Thickness of Ice Sheet (M) 400 m.

Tables I and II
Fraction of the upward flow of heat through the base at the centre of an ice sheet passing through a horizontal surface at a height h above the base.
The rate of outflow of geothermal heat (q) is roughly uniform over the world at about 38 cal./cm.2/year Reference Jeffreys 6 which gives a gradient of 1° C. per 44 m. at the base of the ice sheet. By integration of (6) we find that the temperature difference between any height h and the surface of the ice sheet is
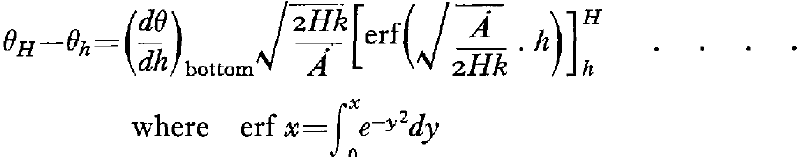
Results corresponding to a number of different values of annual accumulation are shown graphically in Figs. 2 and 3 (p. 527), corresponding to values of H of 3000 m. and 400 m. respectively, taking q as 38 cal./cm.2/year.
Equation (8) gives an estimate of ice temperature only if the calculated value of the bottom temperature (θ b.c. ) is equal to or below the melting point of the ice at the appropriate pressure (θ m ). If the value of θ b.c. is above θ m then it appears that bottom melting will take place. As relative changes in temperature gradients will remain the same, all the excess supply of geothermal heat should be used in bottom melting. Equation (7) should then be modified to allow for this effect and becomes

while the heat being used for bottom melting is

The foregoing considerations are also relevant to small polar (cold) glaciers in those regions where the ice movement is small, for example in a large, flat firn field feeding a glacier. Mr. Joel E. Fisher has pointed out, and his results on pages 583–91 of this Journal indicate, that in mountain glaciers, where appreciable areas of nearby rock are exposed, conduction of heat through the rock plays an important part, and may lower the basal ice temperature.
Heat Supply and Effect of Ice Movement Away from Centre of Ice Sheet
In discussing the results of the German Greenland expedition,Reference Brockamp 1 , Reference Brockamp 2 Brockamp has considered that internal friction due to settling and sinking of the snow should provide a considerable source of internal heat. He shows that the change in potential energy as the ice sinks is sufficient to produce a temperature gradient of 0.5° C. per 100 m. throughout the ice mass. However, it follows from the more detailed study of ice motion made by Nye Reference Nye 4 that the available “potential energy” due to the outward and downward movement of the ice mass is mainly used in producing relatively rapid shear in the bottom layers of ice, with very little shear at higher levels. It seems reasonable therefore to interpret the work done in producing this shear as producing the equivalent amount of heat at the ice-rock interface, rather than as distributed throughout the ice mass as Brockamp has done. As Nye Reference Nye 5 has shown that the shearing stress at the bed of the Greenland Ice Cap is approximately constant at 0.88 bars, we can calculate the work done in unit time (W)
where v is the velocity of ice movement above the bed. Converting this into calories, we find that the additional heat supply for an ice movement of 10 m. per year=21 cal./cm2/year or that our heat supply due to an ice movement of 18 m. per year will equal the geothermal heat supply (taken as 38 cal./cm.2/year).
To consider the temperature distribution away from the centre of the ice sheet, we must take into account this extra source of heat. We must also consider different effects due to ice movement. In addition to the settling of ice due to accumulation, as described by equation (1), we have a downward movement of ice, due to its outward motion to regions where the total thickness of ice is less.
If other factors such as surface temperature and heat supply did not change, we could deal with this problem by considering the extra downward movement of the ice as equivalent to an extra accumulation at the surface. However, this is not the case, but it follows that our limit of penetration of heat from the base of the ice sheet as shown in Tables I and II will be lowered. We can therefore use these tables as an upper limit of such penetration over the whole ice sheet, as a calculation of this limit away from the centre is not attempted in this paper. We can also estimate the maximum possible gradient at the bottom of the ice sheet away from its centre from equation (10) plus the geothermal heat flux. A rough estimate of the speed of ice movement due to accumulation indicates that results from (8) will approximately apply for a distance of about 1/10 to 1/5 of the radius of the ice sheet around its centre. Also within a few kilometres of the centre of an ice sheet, our mechanism differs very much from that outlined by Nye, so some differences may arise here.
Downward Heat Flow from Surface
In addition to the factors mentioned so far, the temperature of the surface layers of ice and firn varies with its height above sea level. Brockamp 1 gives 0.9° C. per 100 m. elevation as the change in ice temperature due to height which agrees approximately with the Antarctic results of Schytt Reference Schytt 10 . Due to outward and downward movement of ice away from the centre of the ice sheet, the mean temperature at which each annual layer of firn accumulates will be slightly warmer than that of the layer of firn of the previous year. In the simplest case, where the velocity of ice movement is V, the surface slope α, the net rate of accumulation

provided α is small.
We can estimate the magnitude of this effect for our simplified ice sheet as follows:
Differentiation of (1) gives



This simple expression indicates that one should get an increase in the negative temperature gradient close to the surface as one moves out from the centre of an ice sheet, provided the upward flow of heat from the base is negligible. If the upward flow of heat is appreciable, one would anticipate a decrease in the negative gradient shown by (11) or (14), a positive gradient being formed when the upward flow of heat outweighs this tendency to form a negative gradient. While (14) indicates the order of magnitude of such a negative gradient close to the surface, it does not take account of thermal conduction. This has been done however for one paricular case later in this paper.
Comparison with Observed Temperatures
Bottom Temperatures
Near the centre of the Greenland Ice Cap we can take H = 3000 m., A = 30 cm. per year and the surface temperature θ H = 29° C. Use of Fig. 2 or equation (8) then gives a bottom temperature of about −12° C. Both Haefeli Reference Haefeli 11 and Holtzscherer Reference Holtzscherer 12 conclude that the base of at least part of the ice sheet is below freezing point. Holtzscherer estimates the basal temperature near the centre at around −10° C. from seismic shooting information. Away from the centre Haefeli believes the bottom temperature may rise to freezing point, but Holtzscherer’s refraction shooting results indicate a layer which may consist of frozen moraine or similar material at Camp IV and VI near the edge of the ice sheet.
Qualitatively this paper agrees with the picture presented by Haefeli, as it suggests that the basal temperature will increase as we move out from the centre of the ice sheet. However, Holtzscherer’s observations suggest that this increase is not sufficient to raise the basal temperature to melting point.
In the case of a small ice hill Reference Robin 13 near the base of the Norwegian British Swedish Antarctic Expedition 1949–52, with an annual accumulation around 40 cm. of ice, one would expect a basal temperature around −14° C. as the data in Fig. 3 fit this case. Calculations of the shear stress at the base of the ice hill suggest that the ice there is a few degrees below melting point.Reference Robin 13
Temperature Gradients near the Surface
Measurements of temperature gradients close to the surface are available. Ahlmann Reference Ahlmann 15 has summarized earlier measurements, and works presented by Bauer Reference Bauer 14 and Heuberger,Reference Heuberger 17 Schytt,Reference Schytt 10 and Fisher Reference Fisher 7 , Reference Fisher 8 , Reference Fisher 9 give more recent data. Temperature gradients obtained by the German Greenland expeditions Reference Ahlmann 15 close to the edge of the ice sheet at Borg in 1912–13 and West Station in 1931 were found to be four or five times the anticipated gradient due to the geothermal supply alone. This appears to fit the concept of a heat supply due to the rapid shear in the lowest layers of ice, but it will also be due in part at least to the increase of temperature gradient caused by the relatively rapid thinning of the ice during it’s outward motion. The negative gradient first suggested by the German results at Eismitte has now been confirmed and amplified by the results of Expéditions Polaires Françaises Reference Bauer 14 , Reference Heuberger 17 . Comparison of their results with those given by equation (14′) are shown below:

Qualitatively the increase in negative gradient with distance from the centre of the ice sheet is shown, but the quantitative agreement is not good.
In the case of Camp VI, a more detailed analysis than that given by (14) has been made, which also takes into account the term due to thermal conduction.
We make the simplifying assumption, that as the ice moves outwards over a limited region the temperature gradient near the surface remains constant, although the temperature as a whole changes in proportion to the change of surface elevation, then we can express the heat balance by the equation as follows:

The coefficients in (15) can be determined for a given temperature depth curve by fitting the polynomial
to a series of points on the observed curve. From these points the coefficients in (15) can be determined. This has been done for the smoothed temperature-depth curve published by Bauer Reference Bauer 14 for Camp VI. Two sets of results were obtained by including terms of the third degree in (16) as follows:

using C.G.S. units.
Taking k = 1.18 × 10−2 cm.2/sec. as the value for ice,
and H = 1370 m.—as measured by seismic shooting,
we get
This agrees reasonably well with the observed accumulation.
If we take α=0.01 radians (as indicated approximately on Holtzscherer’s profile)
and λ = 9 × 10−5° C.
we get V = 113 m. per year.
For comparison equation (2) gives V = 100 m. per year if we take A =30 cm. per year and r = 450 km. This figure is probably too high, as at Camp IV the observed surface movement Reference Bauer 14 was 30 m. per year compared with a calculated movement of 196 m. per year.Reference Bauer 14 However, in view of the presence of streams of faster flowing ice in the ice sheet,Reference Bauer 14 we cannot base conclusions on the surface velocity at Camp VI on observations at Camp IV. A more accurate calculation should also allow for the effect of climatic change on the shape of the temperature-depth curve.
No attempt has been made to use observations at Station Centrale to determine probable accumulation and velocity, as the form of the temperature-depth curve there would not give consistent results over different sections of the curve. Instead it appears that climatic changes have more effect on the shape of the curve than the slight effect given by (14). The upper portion of this curve would certainly agree with the hypothesis of a warming of this region in recent decades, and could perhaps be used to make a quantitative estimate. In addition, the slight temperature-depth change shown on this curve agrees within limits such as may be imposed by the above factors with the appropriate temperature-depth curve of Fig. 2.
Fisher Reference Fisher 7 , Reference Fisher 8 , Reference Fisher 9 has provided figures for the temperature-depth variation of the cold glacier on the north face of Monte Rosa. The temperatures observed in his 1952–53 tunnel fit (11) qualitatively at least, but the picture for the 1954 tunnel is too complicated to agree with this analysis.
The curves for the U.S. West Base in 1940,Reference Ahlmann 15 and for Maudheim in 1951 Reference Schytt 10 are those for floating ice shelves. The problem is somewhat different, and instead of assuming a constant geothermal supply of heat, we can assume a constant temperature of the base of the floating ice shelf equal to the freezing point of sea water. In Fig. 4 (p. 531) two curves have been calculated for Maudheim. For curve (1), it is assumed no bottom melting of the ice shelf occurred, and the ice shelf was assumed to spread out so that equation (1) applied. For curve (2) the bottom melting of the ice has been assumed equal to the surface accumulation so that equation (1) now becomes


Fig. 4. Temperature-depth curves for ice shelves.
-
A. Maudheim, 1951, observed.
-
B. Bay of Whales, 1940, observed.
-
Maudheim, calculated for no bottom melting.
-
Maudheim, calculated for bottom melting equal to accumulation
-
Neither curve (1) nor curve (2) fits the observed value at Maudheim, but (2) seems to fit the observed values at the Bay of Whales (U.S. West Base) if we assume that accumulation and ice thicknesses are similar, which is very approximately true.
It appears the ice movement and accumulation at Maudheim are not entirely in a state of equilibrium as defined by these hypotheses. Other factors which we should also consider are changing surface temperatures of ice shelves due to their northward motion and increasing proximity to the sea, or due to climatic change. Also a considerable time would be needed for inland ice pushed out into an ice shelf to attain thermal equilibrium under the new conditions.
As regard applying figures obtained in Greenland to our basic assumption of a stable ice sheet, it is worth noting that Bauer Reference Bauer 14 estimates that the Greenland ice sheet is losing ice equivalent to 100 Km.3 per year in a total annual budget of around 500 Km.3. The accuracy of the observations is not sufficient to definitely exclude the possibility that the ice sheet is stable, as was earlier proposed by Loewe.Reference Loewe 18 Gravitational observations over the Greenland Ice Cap made by Expéditions Polaires Françaises, and the British North Greenland Expedition should help to show whether or not the ice sheet is in isostatic equilibrium, and consequently whether the ice sheet has been relatively stable over a long period.
Temperature Distribution in The Ice Cap of Central Greenland
To estimate the temperature distribution throughout an entire ice sheet involves studying the integrated sum of all the factors previously mentioned on a column of ice during its journey from the centre to the boundary of the ice sheet. The picture is a complicated one, but Fig. 5 (p. 531) provides a sketch which attempts to combine the observations near central Greenland with the arguments in this paper.

Fig. 5. Sketch of the temperature distribution in a simplified ice sheet similar to central Greenland
Consequences of Proposed Hypotheses
(a) Basal temperatures of ice sheets
At the centre of the Greenland Ice Cap, if the accumulation dropped to 10 cm. of ice per year, the basal temperature for equilibrium would rise to 0° C., and any further drop would result in melting of the base of the ice at the centre of the ice sheet. Our estimate of the magnitude of the geothermal heat flow here is of course very approximate. However, the decrease in accumulation believed to occur as one moves further north over the ice sheet may produce a rise in basal ice temperature in spite of lower surface temperatures. This would facilitate the flow of ice and may help to explain the lower height of the ice sheet in northern Greenland on the basis of the work of Nye Reference Nye 4 and Glen Reference Glen 19 even though the base of the ice sheet remains at around sea-level according to Holtzscherer,Reference Holtzscherer 12 contrary to Nye’s predictions.Reference Nye 5 An alternative explanation for the difference between the north and south of the Greenland Ice Cap could be that the two portions are in different phases of long-period cyclic variations of thickness as outlined below in section (b). The gravitational observations previously mentioned should help settle this point.
(b) Catastrophic advances of glaciers
If circumstances outlined in this paper produce basal ice temperatures below melting point, a greater shear stress will be required to produce ice flow. This means that greater surface slopes and ice thickness will be formed. Now if the basal ice temperature in such an ice sheet or glacier is raised by some phenomenon—the most likely one being by an increase in ice movement over the bed—the shear stress due to the greater ice thickness formerly accumulated will be in excess of that required to make the ice flow at this higher temperature. As this is an unstable state the flow may continue to increase until the basal temperature reaches melting point, leading finally to a relatively rapid advance of the glacier front. With basal temperatures now at melting point the flow and ice thickness may remain similar to that of a temperate glacier until conduction and the downward “advection” of cold ice again start to lower the temperature of the ice rock interface with consequent thickening of the glacier. Such a chain of events may well be cyclic with a very long period. The mechanism may be the explanation of such catastrophic glacier advances as those of Bråsvelbreen in Svalbard and of the Kutiàh Glacier Reference Desio 20 in the Karakoram recently.
Such a mechanism may not be uncommon in polar glaciers. Ahlmann Reference Ahlmann 16 in his Bowman Memorial lecture on Glacier Variations and Climatic Fluctuations says the following:
“It has already been mentioned that in Spitsbergen conditions are in many respects peculiar. A summary prepared for me by Liestöl, points out that glacier snouts that have receded over a hundred years or so, suddenly begin a rapid advance, sometimes reaching as far as the outermost, recent teminal moraines. Every glacier has its own period of variation, which is, however, dependent on the more pronounced climatic fluctuations and changes.”
Both Matthes and Liestöl are quoted by Ahlmann as putting forward similar explanations for such surges. He quotes Liestöl as follows:
“Over a long period of time a surplus may be built up in the accumulation area, while the lower part of the glacier concurrently wastes away until the frictional limit is exceeded, and the ice slides forward. Such a condition, he says, is most evident in polar and sub-polar glaciers and, it may also be added, is especially applicable to glaciers whose accumulation areas are situated on plateaus high above the valleys constituting their main ablation areas.”
Thus the existence of such long-period surges has been observed and an explanation has been outlined. The importance of the temperature variations of the bed of the glacier has not however been stressed, but it appears to provide the essential key to the mechanism. It is admittedly difficult to prove this by direct measurements of basal ice temperatures, but observations may be possible on the base of glaciers which have recently surged forward. It would of interest to know whether such surges also appear as intermittent ice streams, large or small, flowing out of the main Antarctic and Greenland ice sheets.
The exceptional advance of the Kutiàh glacier, reported by Professor A. Desio Reference Desio 20 in this Journal appears to fit into the pattern of Spitsbergen glaciers as outlined by Liestöl. One concludes that the glaciers feeding it must have an interconnected accumulation zone of sufficient elevation, say 6000 m. or more, to ensure the supply of firn being appreciably below freezing point. Also one would presume that this high accumulation zone is sufficient in area, say three square kilometres or more, to provide the large volume of ice necessary for the reported advance. At present there is no evidence to show that the Kutiàh glacier has previously shown such an exceptional advance, but a search for such evidence, and a knowledge of the accumulation zone of the glacier, would obviously help our understanding of this advance. In such an area with a considerable expanse of exposed rock, climatic change may trigger off an advance more quickly by conduction of heat through the rock, rather than by the slow process of modifying the firn temperatures. This would agree with Professor Desio’s proposed explanation.
While this paper has not given the full solution to a complex problem, I hope it has drawn attention to the large effect of ice movement on the transfer of heat. Further field results are needed which include measurements of surface velocity in addition to accumulation and temperature gradient data.
I wish to acknowledge the help of Dr. G. Field in fitting equation (14) to field measurements, and of an Imperial Chemical Industries Research Fellowship during the tenure of which the ideas outlined in this paper were formed.