1. Introduction
Motivated primarily by investigations of global change, the scientific community has become increasingly aware that low-latitude mountain environments are highly sensitive indicators of climate change (e.g. Reference ThompsonThompson and others, 1995; Reference BroeckerBroecker, 1997). Glaciers, especially, have become the subject of intensive observation. Corresponding to global trends, they have retreated significantly since the mid-19th century (e.g. Reference HastenrathHastenrath, 1995; Reference KaserKaser, 1999). Several analyses show that it is not only increased temperature and/or decreased precipitation that are responsible for these retreats, but also changes in air humidity (Reference Kaser and NogglerKaser and Noggler, 1991; Reference Hastenrath and KrussHastenrath and Kruss, 1992; Reference Kaser, Georges and AmesKaser and others, 1996b; Reference Kaser and GeorgesKaser and Georges, 1997; Reference KaserKaser 1999; Reference Wagnon, Ribstein, Kaser and BertonWagnon and others, 1999).
A few attempts have been made to derive climate scenarios from reconstructed paleo-glaciations in low latitudes (e.g. Reference Klein, Seltzer and IsacksKlein and others, 1999; Reference Hostetler and ClarkHostetler and Clark, 2000), but they do not deal adequately with the particular circumstances of different low-latitude glacier regimes. In this paper I outline these regimes and propose a model which simulates the basic characteristics of low-latitude glacier–climate interaction. Different climate regimes and their respective glacier regimes are distinguished and defined. Then the model and the derived vertical profiles of specific mass balance (VBPs) for each regime are presented, and the model results are compared with the few available measured VBPs. Finally, the sensitivity of the equilibrium-line altitude (ELA) of low-latitude glaciers to changes in various climate variables is discussed. Preliminary elements of this concept, concerning the tropics, were published earlier (Reference KaserKaser, 1995; Reference Kaser, Hastenrath and AmesKaser and others, 1996a). The concept is herein extended to the subtropics.
2. Climate and Glacier Regimes at Low Latitudes
The following is a generalized and simplified depiction of climate regimes at low latitudes. Although there are various deviations from this idealized scheme in reality, the simplifications are justified by the attempt to address the basic differences between the regimes.
Two principal features of global zonal circulation characterize low latitudes, the Inter-Tropical Convergence (ITC) and the trade winds. Whereas the ITC is part of a humid climate, trade winds are connected with particularly dry conditions. The respective climate zones are known as the tropics and the subtropics. The annual cycle of solar radiation leads to an oscillation in the dynamic circulation pattern, which is smaller above water surfaces and greater on continents. Hence, only the inner tropics have continuously humid conditions. At the outer limits of the tropics, there is only one rainy season per year. Thus, the outer tropics can be treated as an intermediate zone between the tropics and the subtropics; during the humid season they have tropical conditions, and during the dry season, subtropical conditions.
From the glaciological perspective of this paper, the following requirements must be met for an area to be considered to lie in the tropics (inner and outer): it must be within: (i) the astronomical tropics (radiative delimitation); (ii) the area where the daily temperature variation, ΔT d exceeds the annual temperature variation, ΔT y (thermal delimitation); and (iii) the oscillation area of the ITC zone (ITCZ) (hygric delimitation) (Reference KaserKaser, 1995; Reference Kaser, Hastenrath and AmesKaser and others, 1996a). The resulting delimitations for tropical glaciers and the distribution of glacier area by country are shown in Figure 1. The ITC and the frontal activities of the westerlies reach the subtropics only sporadically. Thus the subtropics are quite dry. The seasonality of low latitudes can only be delimited by hygric considerations as there is an absence of major thermal seasonality. As a model assumption, this applies to the area where daily variations of air temperature exceed annual variations. This area, especially over South America, reaches rather far into the subtropics (Fig. 1). Hence, three glacier regimes can be derived:
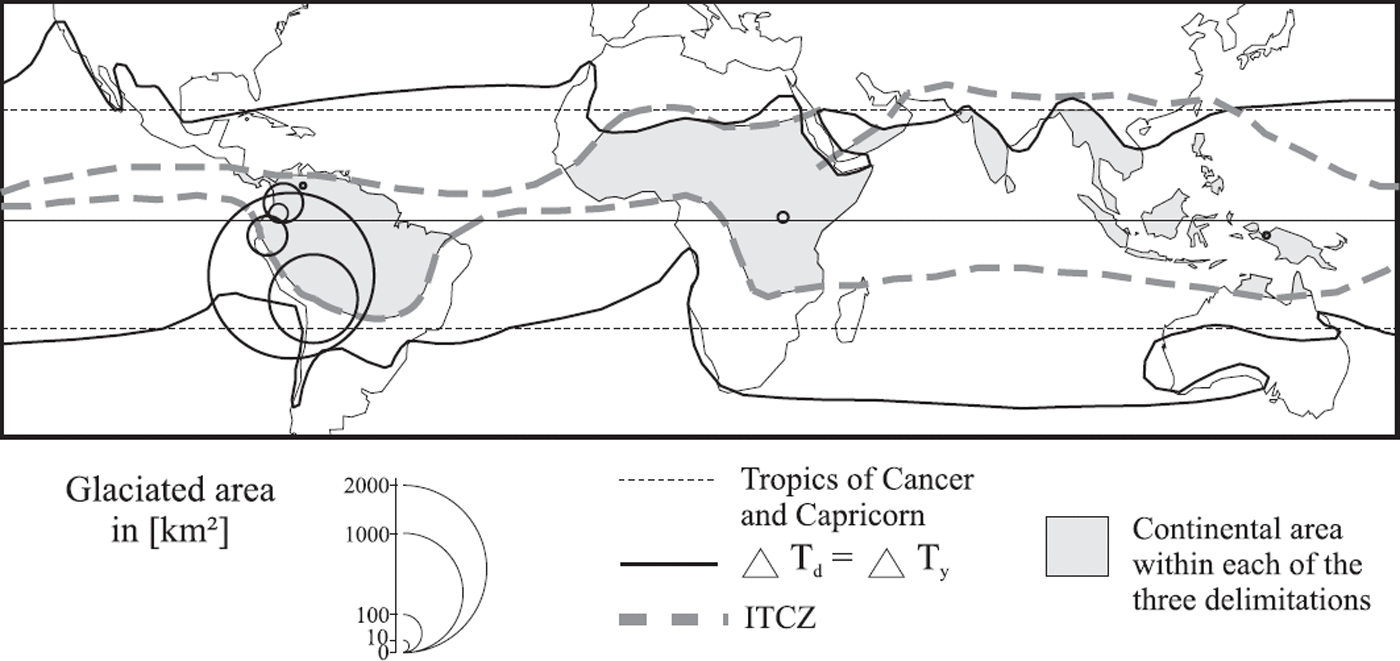
Fig 1. The tropics and their delimitations from a glaciological point of view, and the distribution of glacier areas by country (after Reference Kaser, Hastenrath and AmesKaser and others, 1996a). The circles are centered on the respective country with the exception that all East African glaciers are represented by a single circle. The bold dashed lines show the boundaries of the seasonal oscillation of the ITCZ.
In the humid inner tropics, stable humidity and temperature conditions cause accumulation and ablation to occur simultaneously throughout the year. Such conditions can be expected on the Ruwenzori Mountains in East Africa, and on Irian jaya in New Guinea (Reference Kaser, Hastenrath and AmesKaser and others, 1996a).
In the outer tropics, notable accumulation occurs only during the wet season. During the dry season, there is little or no accumulation, and ablation is also reduced. Because of the dry air, much of the available energy is consumed by sublimation, and therefore little remains for melting. This has been shown by Reference Kaser, Ames and ZamoraKaser and others (1990) through an analysis of ablation measurements from glaciers of the Cordillera Blanca, and by Reference Wagnon, Ribstein, Kaser and BertonWagnon and others (1999) through energy-balance investigations on Glaciar Zongo, Bolivian Cordillera Real. It is noteworthy that most of the tropical glaciers are found in the outer-tropical regime mainly because of the meridional lengthening of the austral summer ITCZ over South America (Fig. 1).
Under extreme subtropical conditions, as in southern Bolivia and northern Chile, almost all ablation can be presumed to result from sublimation (Reference KnocheKnoche, 1931). The sparse accumulation is from sporadic precipitation which is distributed over the year and is related to either the ITCZ or the westerly frontal zone (e.g. Reference Vuille and AmmannVuille and Ammann, 1997). The annual temperature variation increases with latitude, so the ablation season becomes slightly shorter than in the tropics.
Thus, two variables describe the principal differences between the three low-latitude glacier regimes and serve to distinguish them from mid-latitude conditions: (i) the ratio of melting to sublimation, and (ii) the duration of the ablation period. These two variables are vital components of any model which seeks to depict the characteristic differences of such glacier regimes.
3. Modelling the VBP
The VBP of a glacier is the variation of the specific mass balance with altitude (i.e. the vertical profile of specific mass balance). The VBP emphasizes the relation between a glacier and its climatic setting. The climatic setting is a combination of widely homogeneous regional factors which can be parameterized from variables of the free atmosphere, and local factors which are unique for each glacier. Both have been discussed and introduced in glacier climate models of varied sophistication (Reference KuhnKuhn, 1981,Reference Kuhn and Oerlemans1989; Reference Oerlemans and OerlemansOerlemans, 1989; Reference Oerlemans and HoogendoornOerlemans and Hoogendoorn, 1989; Reference Ohmura, Kasser and FunkOhmura and others, 1992).
Here, the glacier–climate interaction is simplified to the regional climate variables since the aim of the model is to depict the characteristic differences between large-scale glacier regimes. A synthetic VBP is first modelled and calibrated for a mid-latitude glacier (Hintereisferner, Austrian Alps) from selected variables. The model is then exposed successively to inner-tropical, outer-tropical and subtropical conditions. The basic structure of the model is adopted from Kuhn’s model describing the response of the ELA to climatic fluctuations (Reference KuhnKuhn, 1981, Reference Kuhn and Oerlemans1989).
The specific mass budget b at any altitude z on a glacier over a specific period is composed of the sum of specific accumulation (c(z), positive) and specific ablation (a(z), negative)
The vertical mass-balance gradient is thus
with positive z vertically upward. The differential of the specific balance is then
Ablation at any given altitude results from the available heat flux per horizontal surface unit, Q A, in J m−2 d−1, thus:
where L is the heat of fusion (L M = 0.334 MJ kg−1) and/or sublimation (L S = 2.835 MJ kg−1), and τ(z) is the duration of the ablation season at the given altitude, in days. Consistent with Equation (1), a(z) is negative, so all heat fluxes toward the surface are positive. In a linear approximation, τ(z) can be calculated from a given τ(z ref) at a reference altitude as
The duration of the ablation period τ must be known in order to convert energy into mass-balance terms. It is not an entirely independent variable but should always be treated together with the mean energy flux over that period. If, hereinafter, τ is changed while the energy fluxes are kept constant, a constant daily mean of the energy fluxes over different time periods and at different altitudes is assumed for simplification.
The vertical ablation gradient at a given altitude z is

Considering that (1/L) Q A(z) = a(z)/τ(z), Equation (6) becomes

For the large-scale regional objectives of this model, which is intended to calculate the shape but not the absolute position of the VBP, the following are assumed:
The sensible-heat flux is described by C S[∂(T a − T s)/∂z],where C S is the heat-transfer coefficient for turbulent exchange of sensible heat between atmosphere and glacier surface, in MJ m−2 d−1 °C−1. Under melting conditions, the term is reduced to C S ∂T a/∂z; ∂T a/∂z is the atmospheric lapse rate. Under non-melting conditions the vertical gradient of the surface temperature is ∂T s/∂z = ∂T a/∂z; thus the vertical gradient of the sensible-heat flux becomes 0. The value of C S is discussed below.
Similarly, the vertical gradient of the net longwave radiation is reduced to the incoming flux under melting conditions. The incoming longwave radiation is, using a linearized form of the Stefan–Boltzmann equation, 4ε a σ(273.15)3 ∂T a/∂z, where ε a is the emissivity of the atmosphere and σ is the Stefan–Boltzmann constant. By analogy to the heat-transfer coefficient, the constant part of the equation is 4ε a σ(273.15)3 = C R = 0.28 MJ m−2 d−1 K−1 with ε a = 0.7 and σ = 4.9 × 10−9 MJ m−2 d−1 K−4. The vertical gradient of the incoming longwave radiation thus obtained matches well the measured values reported by Reference MullerMuller (1984). Again, if the surface is frozen, ∂T a/∂z = ∂T s/∂z and the vertical gradient of incoming longwave radiation is compensated by the gradient of longwave emission. Thus, no input to the model comes from net longwave radiation.
The vertical gradient of the global radiation, ∂G/∂z, is 0. Mean values of albedo, α, on snow and ice have been known for some time (e.g. Reference Sauberer and DirmhirnSauberer and Dirmhirn, 1952; Reference WagnerWagner, 1979). At the transient snowline, the albedo of a glacier surface changes more or less abruptly from low values on bare ice (α ice) to the relatively high values of the snow surface (α snow). If the snowline is assumed to rise more or less continuously, at a rate dz/dt, from the tongue to its highest position (equal to the ELA) during an ablation season of length τ, the annually averaged vertical gradient of albedo is approximately

Above the ELA, ∂a/∂z = 0.
The contributions of melting and sublimation to ablation are described by the term

where

L M and L S are the heat constants for fusion and sublimation, and Q M and Q L the heat fluxes consumed by melting and sublimation. It is stressed that this approach ignores a possible variation of the ratio f with elevation. However, it allows for the consideration of sublimation as a crucial variable when comparing humid and dry climates. The reference level, z ref, from which calculations start is defined as the elevation at and above which ∂a/∂z = 0 kg m−2 m−1. This does not necessarily mean that a = 0 kg m−2. From z ref, calculations proceed upward (z = +) and downward (z = −). It is assumed that ∂T s/∂z = ∂T a/∂z above the mean 0°C (273.15 K) level of the ablation period. Consequently, the vertical gradient of the sensible-heat flux becomes zero and the vertical gradient of the incoming longwave radiation is compensated by the gradient of longwave emission. ∂a/∂z becomes zero above the ELA. Thus, ideally, z ref, the 0°C level and the ELA should all be the same altitude. On the mid-latitude Hintereisferner, the mean ELA lies clearly below the mean 0°C level of the mean ablation period (from longterm ELA and temperature records in Reference Kuhn, Kaser, Markl, Wagner and ScheiderKuhn and others (1979)). The same is true in the inner tropics (Reference KuhnKuhn, 1980; Reference Ohmura, Kasser and FunkOhmura and others, 1992). Hence, z ref is set equal to the altitude of the mean 0°C level for the VBP model of both the mid-latitude Hintereisferner and the inner-tropical glaciers. The area over which ∂a/∂z > 0 is thereby extended up to the 0°C level, leading to an overestimate of the gradient in specific mass balance in this altitudinal step. In the subtropics, the ELA lies up to 1 km above the 0°C level (Reference KuhnKuhn, 1980; Reference Ohmura, Kasser and FunkOhmura and others, 1992), so z ref = ELA.
Thus, the vertical gradient in ablation at any altitude, z = − (i.e. below the equilibrium line (EL)), is

where the contributions to the vertical gradient in the energy for ablation, ∂Q A/∂z, are reduced to those from the vertical gradients of the net global radiation, the incoming longwave radiation and the sensible-heat flux. From Equation (3), the change in specific mass balance between discrete altitude steps Δz, above and below any level z, is then

3.1. The VBP in the mid-latitudes
Let us now calculate a VBP from climatic data and calibrate it with a measured profile. Both the climate data and the measured profile are from the Hintereisferner. Based on Reference KuhnKuhn (1979, Reference Kuhn1981), Reference Kuhn, Kaser, Markl, Wagner and ScheiderKuhn and others (1979), Reference WagnerWagner (1979) and some additional references mentioned below, the following model input data are representative for Hintereisferner under mass-equilibrium conditions:
The mean duration of the annual period of ablation at the altitude of the summer mean 0°C level (June–September) is τ ref = 100 days. This is thought to be the number of days, not necessarily successively, during which ablation takes place.
The duration of the ablation period changes with the altitude at a rate of ∂τ/∂z = −0.1 day m−1.
Accumulation increases with altitude at a rate of ∂c/∂z =1 kg m−2 m−1.
The air temperature decreases with altitude at a rate of ∂T a/∂z = −0.0065 °C m−1.
At Hintereisferner, the ELA is about 100–150 m below the summer mean 0°C level. Because we do not have sufficient knowledge, annual ablation at the altitude of the summer 0°C level, a(z ref), is approximated by the ablation at the mean EL. This, in turn, is equal to the accumulation there, which is approximately 1600 kg m−2 at Hintereisferner. (Note that the effect of an inaccurate determination of a(z ref) on Δb is small because ∂τ/∂z is small.)
The mean daily amount of energy from global radiation is G = 20 MJ m−2 d−1.
Reference MullerMüller (1984) gives a compilation of measured albedo values for different Alpine glacier surfaces including Hintereisferner. According to his data the mean values for glacier ice and old snow are α ice = 0.27 and α snow = 0.6, respectively It is further assumed that the snowline rises continuously from the glacier terminus (2450 m) to its location at the end of the ablation season (which is approximately the mean ELA (3050 m)). Thus, dz/dt = 5 m d−1 and ∂a/∂z = 0.000 66 m−1. Even though the albedo changes little above the snowline, ∂a/∂z is kept constant up to z ref. This overestimates db/dz between the ELA and z ref, but the effect is minor when comparing the modelled and measured VBPs in Figure 2.
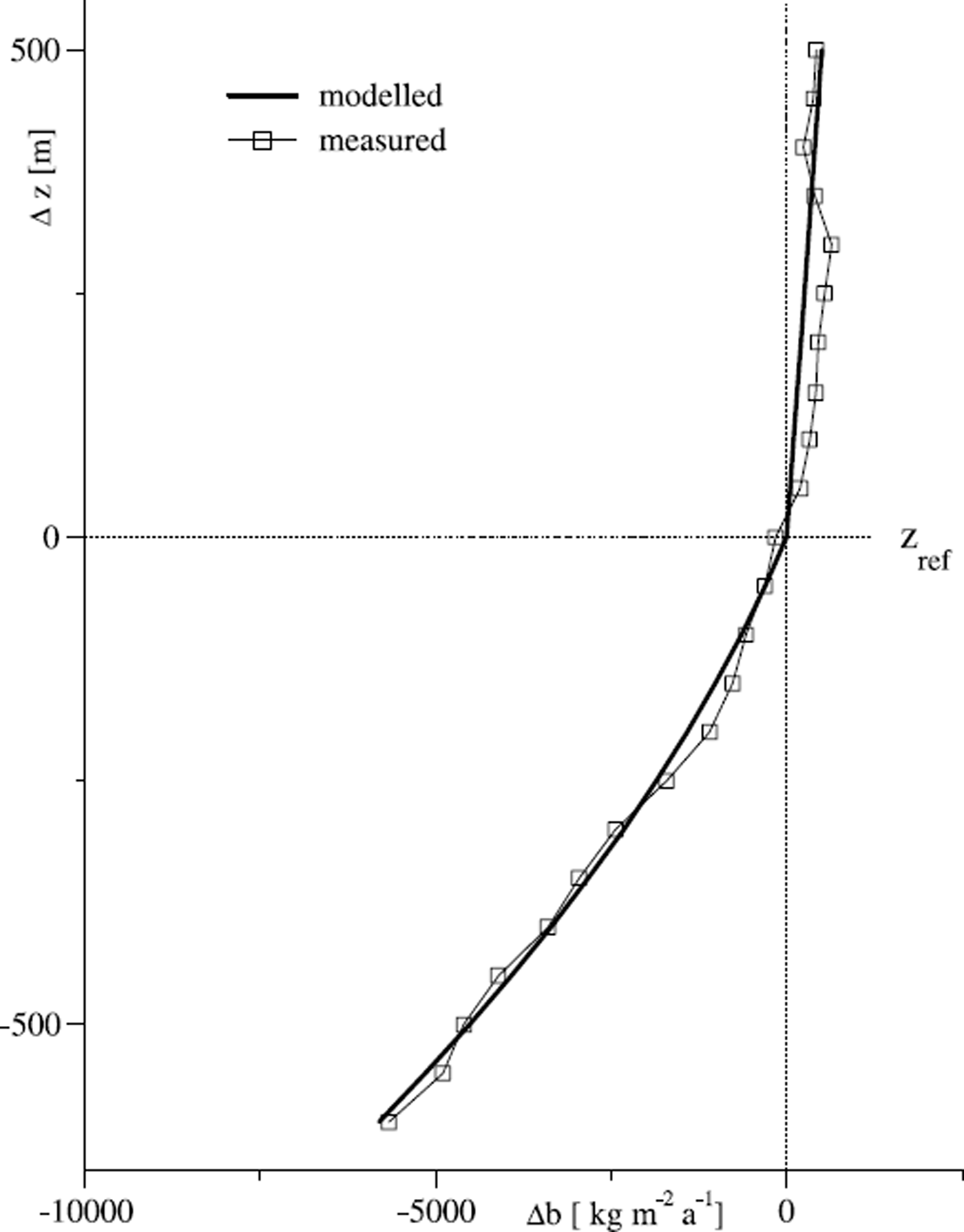
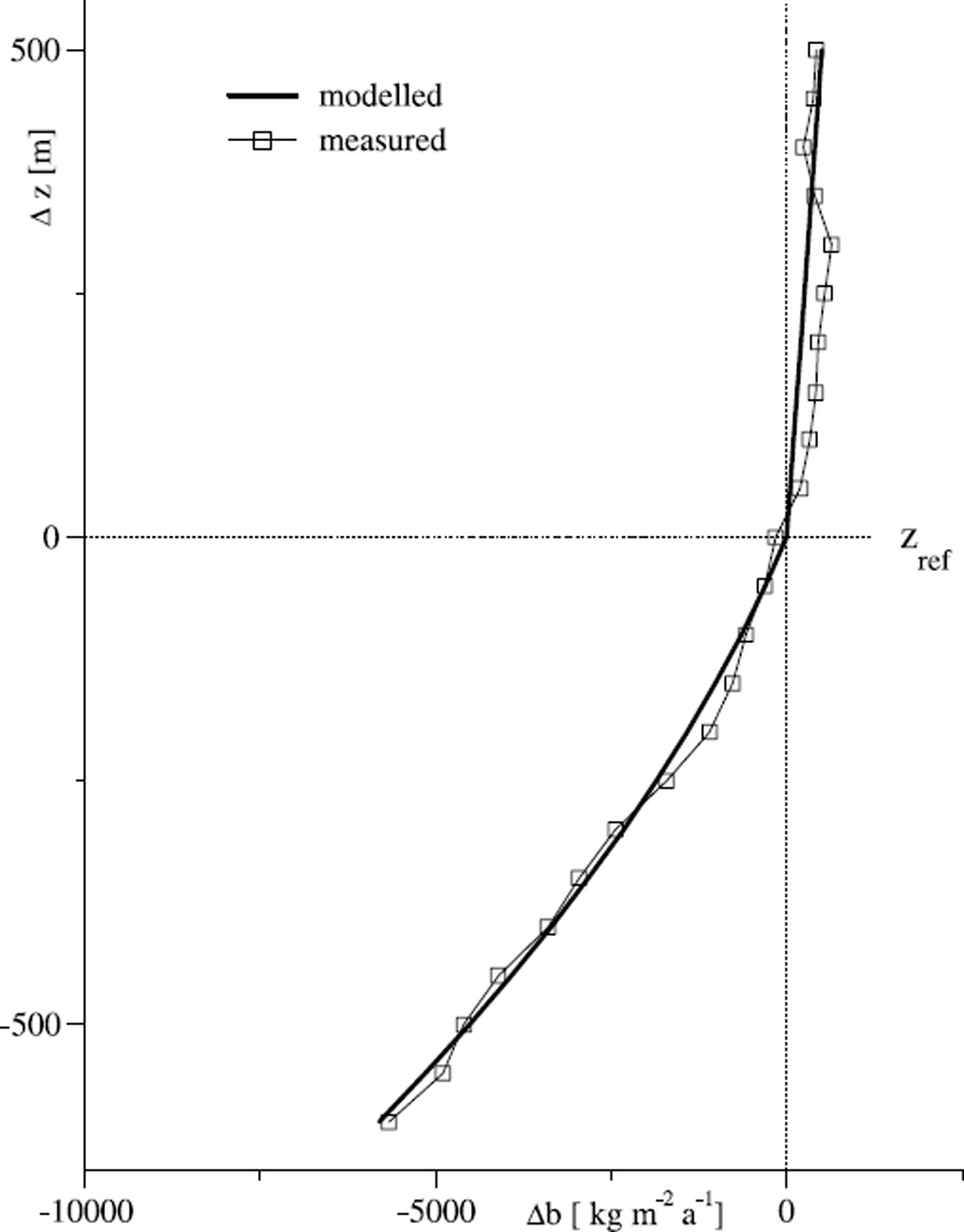
Fig. 2. A VBP calculatedfrom climatic data for Hintereisferner (bold line). Above the reference altitude, z
ref, the profile is influenced only by the accumulation gradient, whereas below z
ref it is affected by both ablation and accumulation gradients. Note that z
ref is at the 0°C level of the ablation period which, on Hintereisferner, is above the EL. The measured profile from the 1966/67 balanced budget year
![]() (thin line with symbols) is fit to the calculated profile by a parallel displacement along the coordinate axes.
(thin line with symbols) is fit to the calculated profile by a parallel displacement along the coordinate axes.
A sublimation rate of 150 kg m−2 a−1 (Reference KaserKaser, 1982, Reference Kaser1984) consumes about 20% of the energy available for ablation on the tongue of Hintereisferner; thus f = 0.2.
While all variables and their variations discussed so far are well supported by measurements, the heat-transfer coefficient C S, being a bulk quantity to parameterize heat conductivity and turbulent exchange in the boundary layer between the surface of the glacier and the atmosphere, has been chosen to fit the model to the measured data. Values empirically obtained above different glacier surfaces range widely from 0.5 to 2.7 MJ m−2 d−1 K−1 (Reference Escher-VetterEscher-Vetter, 1980; Reference FunkFunk, 1985; Reference SchugSchug, 1987; Reference Kuhn and OerlemansKuhn, 1989; Reference TanzerTanzer, 1989). The value for a visual best fit to the shape of the curve in Figure 2 (but not its position) is C S = 1.7 MJ m−2 d−1 K−1, which is close to the arithmetic mean of the reported values. It must be noted that C S not only parameterizes the complex processes of the sensible-heat exchange, but also compensates, to a certain extent, for the omitted changes with altitude.
The values of the variables are summarized in Table 1. Figure 2 compares the modelled VBP with the measured values from the balance year 1966/67, which was a year of nearly balanced mass budget (mean specific mass balance
![]() ). Because the model provides the shape but not the absolute position of the VBP, the measured curve has been shifted along the coordinate axes to obtain a visual best fit to the position. The shapes of the curves agree well; both are characterized by a continuous decrease in the vertical mass-balance gradient with altitude.
). Because the model provides the shape but not the absolute position of the VBP, the measured curve has been shifted along the coordinate axes to obtain a visual best fit to the position. The shapes of the curves agree well; both are characterized by a continuous decrease in the vertical mass-balance gradient with altitude.
Table 1. Variables and constants for the calculation of the mass-balance altitude profile in the mid-latitudes (Fig 2)

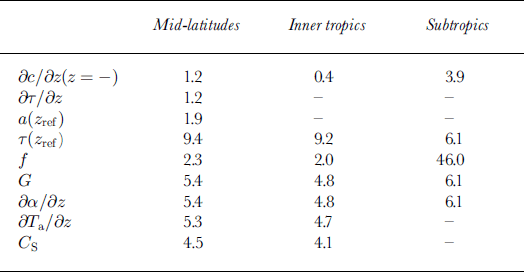
Looking at the different terms in Equation (12), it is obvious that the contributions from the gradients of the sensible-heat flux and the shortwave net radiation to the ablation gradient are about an order of magnitude larger than that of the gradient of the incoming longwave radiation. Together with the factors τ and f, they are the predominant control on the ablation gradient. The accuracy of parameter values and their possible variations are, however, not sufficiently well known. Thus, in order to give an idea of the sensitivity of the model to different input variables, the effect on Δb of a 10% change in each variable is calculated. The results, expressed as a percentage of the original calculated Δb, are shown in the first column in Table 2. The model is most sensitive to changes in τ (9.4%) followed by the shortwave radiation term, G∂α/∂z (5.4%), ∂T a/∂z (5.3%) and C S (4.5%). The effect of the other terms on Δb is minor. The values in Table 2 are also reasonable estimates of the accuracy of most input variables. Exceptions are ∂α/∂z and C S, the values of both of which are educated guesses. However, the strong correlation between the model results and the measured VBP allows the assumption that all input variables are within 10% of their true values. Assuming that the uncertainties in the different input variables are more likely to compensate each other than to accumulate, the accuracy of the modelled VBP is likely to be ±5%. Even though this is strictly true only for Hintereisferner, in the comparison and discussion to follow below, the above-modelled VBP is postulated to be typical for the mid-latitudes.
Table 2. Relative effects on Δb ofa10% change in the variable in column 1, expressed as a percentage of the calculated value of Δb
3.2. The VBP in the inner tropics
For modelling the inner-tropical VBP, it is assumed that the ablation period is τ = 365 days a−1 everywhere on the glacier at and below the z ref. This implies that ∂τ/∂z = 0 and allows simplification of Equation (12). This is the only change relative to the mid-latitude model. The resulting VBP is shown in Figure 3, in which the synthetic profile is compared to those measured on Irian jaya glaciers and on Lewis Glacier, Mount Kenya, both of which are situated close to the Equator.

Fig. 3. Modelled (bold line) and measured (thin lines with symbols) VBPs of tropical glaciers. The measured profilesfor Meren and Carstensz Glaciers, Irianjaya (IJ) and Lewis Glacier, Mount Kenya (MK), are fit to the calculated profile by parallel displacements along the coordinate axes. (MK+) is the VBP for the positive balance year 1988/89
![]() , and (MK−) the VBP for the negative balance year 1986/87
, and (MK−) the VBP for the negative balance year 1986/87
![]() . Mote that z
ref is at the 0°C level which is, on inner-tropical glaciers, above the EL.
. Mote that z
ref is at the 0°C level which is, on inner-tropical glaciers, above the EL.
The Irian jaya VBP is reported by Reference Allison, Hope, Peterson, Radok and AllisonAllison (1976) as an average of measurements on Carstensz (0.9 km2) and Meren Glaciers (1.9 km) and dates from 1972. The annual values for the lowest 200 m in altitude were extrapolated by the authors from 3 months of observation. The specific mean balances were
![]() on Carstensz Glacier and
on Carstensz Glacier and
![]() on Meren Glacier. The mean value of both glaciers, weighted with respect to their relative surface areas, is
on Meren Glacier. The mean value of both glaciers, weighted with respect to their relative surface areas, is
![]() . Thus the mass budget is far from being balanced.
. Thus the mass budget is far from being balanced.
The mass-balance record for Lewis Glacier (0.24 km−2) starts in 1971 (Reference HastenrathHastenrath, 1984, Reference Hastenrath1991; Reference Hastenrath, Rostom and CaukwellHastenrath and others, 1989), but there are no data for a year of balanced mass budget. Since the VBPs have very similar forms for different years, only two curves, one from 1986/87 with
![]() and one from 1988/89 with
and one from 1988/89 with
![]() , are shown in Figure 3 as examples. The sudden increase in the slope of the VBP on the lowest part of the tongue of Lewis Glacier is probably a result of local microclimatological influences.
, are shown in Figure 3 as examples. The sudden increase in the slope of the VBP on the lowest part of the tongue of Lewis Glacier is probably a result of local microclimatological influences.
Simply changing τ yields a modeled VBP that fits measured VBPs almost perfectly. In contrast, to obtain this difference between mid-latitude and tropical VBPs by changing G, ∂α/∂z or ∂T a/∂z, the first two must be multiplied by a factor of 6 and the latter by 7, both of which are absolutely unrealistic.
One might assume that in the constantly humid inner tropics there is no sublimation so f becomes 0. The effect on the VBP could be compensated for by changing the lapse rate from −0.0065 K m−1 to −0.0042 K m−1, by reducing the global radiation to G = 13 MJ m−2 d−1 or by reducing ∂α/∂z to 0.000 43 m−1. The latter could be explained by the fact that the snowline does not rise more or less continuously with time from the terminus to the EL during an ablation season as it does in the mid-latitudes, but rises several times, in steps, during the year. The required values of lapse rate and global radiation are, as a mean, unrealistically low even for humid conditions. If, however, all three of the variables were reduced by 10%, the VBP would be consistent with that reported from Irian jaya.
Again, the sensitivity of the model is tested by changing each variable by 10% and looking at the effect on Δb (Table 2, second column). Although the inner-tropical VBP is less sensitive than that in the mid-latitude, the ranking of the different variables is the same. Assuming a 10% accuracy of the variables, the accuracy of the inner-tropical VBP is, as in the mid-latitudes, about 5%.
In Reference KaserKaser (1995) and Reference Kaser, Hastenrath and AmesKaser and others (1996a) a snow/rain transition zone of 400 m in altitude below the 0°C level was discussed. This would flatten the lower part of the tropical VBP due to an increased gradient of accumulation. Recent field observations in the outer-tropical Gordillera Blanca during the humid season have shown that precipitation falls either as snow or as rain over the entire surface of the tongues. Thus, a gradient of accumulation equal to that in the Alps may remain a best guess. Note also that doubling ∂c/∂z would affect the VBP by only 4%.
With the assumption of constant ablation conditions throughout the year, a VBP is generated which is clearly different from that in the mid-latitudes and shows the basic characteristics of a tropical VBP: compared with the mid-latitudes, the balance gradient below the 0°C level is constant and markedly steeper, and the change to a small balance gradient in the accumulation zone is quite pronounced. It should be noted that if any ablation gradient above the 0°C level were allowed in the model, or if ∂α/∂z exponentially approaches 0 m−1 between ELA and z ref, the sharp change in the tropical VBP would be somewhat smoother and thus closer to the measured VBPs.
3.3. The VBP in the subtropics
There is little general information about glaciers in extremely dry subtropical climates, and no mass-balance measurements. Reference KnocheKnoche (1931) reports exceptionally high sublimation values derived from climate records in northern Chile. Indeed, sublimation can be responsible for all of the ablation. Under such conditions, surface temperatures are kept below freezing much of the time, and the ELA is high above the 0°C level (Reference KuhnKuhn, 1980; Reference Ohmura, Kasser and FunkOhmura and others, 1992). The (negative) surface temperature, T s, decreases further with increasing altitude, so ∂T s/∂z is again approximately equal to ∂T a/∂z, and vertical gradients of both sensible-heat flux and longwave radiation budget are thus zero. Consequently, the respective energy terms in Equation (12) are negligible, as a first approximation. As a consequence, the energy gradient is calculated with only G and ∂α/∂z. This creates the possibility of setting z ref equal to the ELA, above which ∂α/∂z becomes 0. The ablation gradient is additionally determined by the factors f and τ. None of the input variables is reasonably known, and, besides sensitivity analysis, only an educated guess can be offered:
Under subtropical conditions the sublimation/melting ratio is set as f = 1 and τ is set as 300 days a−1. The latter takes the increasing latitude into account, and the accompanying increasing seasonality of insolation. In addition, sporadic snowfalls may interrupt ablation for several consecutive days over the entire glacier. Under such circumstances, a possible but very small value of ∂τ/∂z is neglected. During fieldwork on several glaciers in the Alps and in the Andes, I have observed that the glacier ice surface appears distinctly brighter under sublimation conditions than under strong melting conditions. This is because dry glacier surfaces provide considerable backscattering of solar radiation, due to the presence of dry pores. If, consequently, a higher albedo for ice is used in Equation (8), ∂α/∂z becomes smaller. A value of ∂α/∂z = 0.0005 m−1 is proposed, although it is difficult to approximate any albedo gradient. In addition, global radiation may reach values of G = 30 MJ m−2 d−1 in the subtropics. Inserting these values into the model, db/dz(z = −) becomes almost 9.5 times smaller than it is in the tropics.
The effect on Δb of changing all variables in question by 10% is shown in the third column of Table 2. The most influential term by far is the sublimation/melting ratio, f, which causes a 46% variation whereas the effect of the other terms is, individually, ≤6.1%. No information is available regarding the accuracy of determinations of f in the subtropics, but this example shows how sensitive subtropical glaciers are to changes in air humidity. The subtropical VBP is compared to the VBPs of the mid-latitudes and the tropics in Figure 4. The subtropical VBP has the least change of b with z as a result of the extremely dry circumstances.

Fig. 4. Modelled VBPs for mid-latitude, subtropical and inner-tropical glacier regimes. Note that z ref is at the 0°C level for the mid-latitude and inner-tropical glaciers but is at the EL for the subtropical glaciers.
So far, the modelling has shown that the duration of the ablation period is the crucial variable distinguishing low-latitude from mid-latitude glacier regimes, and that sublimation markedly distinguishes the subtropical regime from the inner-tropical one. Changes of the other variables within realistic ranges are of secondary importance.
3.4. The VBP in the outer tropics
It has been mentioned above that the outer tropics are characterized by tropical conditions during the humid season and by subtropical conditions during the dry season. This not only compels one to look at the outer tropics from two different points of view, but also provides, indirectly, the possibility of examining the subtropical model assumptions.
Modelled VBPs were calculated with the tropical model for the humid season, and with the subtropical model for the dry season, by changing τ to 212 and 153 days a−1, respectively. These values correspond to the situation in the outer-tropical Cordillera Blanca. There, the climate shows almost no annual temperature variation and has one humid season, October–April (212 days), and one dry season, May–September (153 days), which are clearly distinguished from each other (Reference Kaser, Ames and ZamoraKaser and others, 1990). The so calculated VBPs are shown as bold lines in Figure 5.
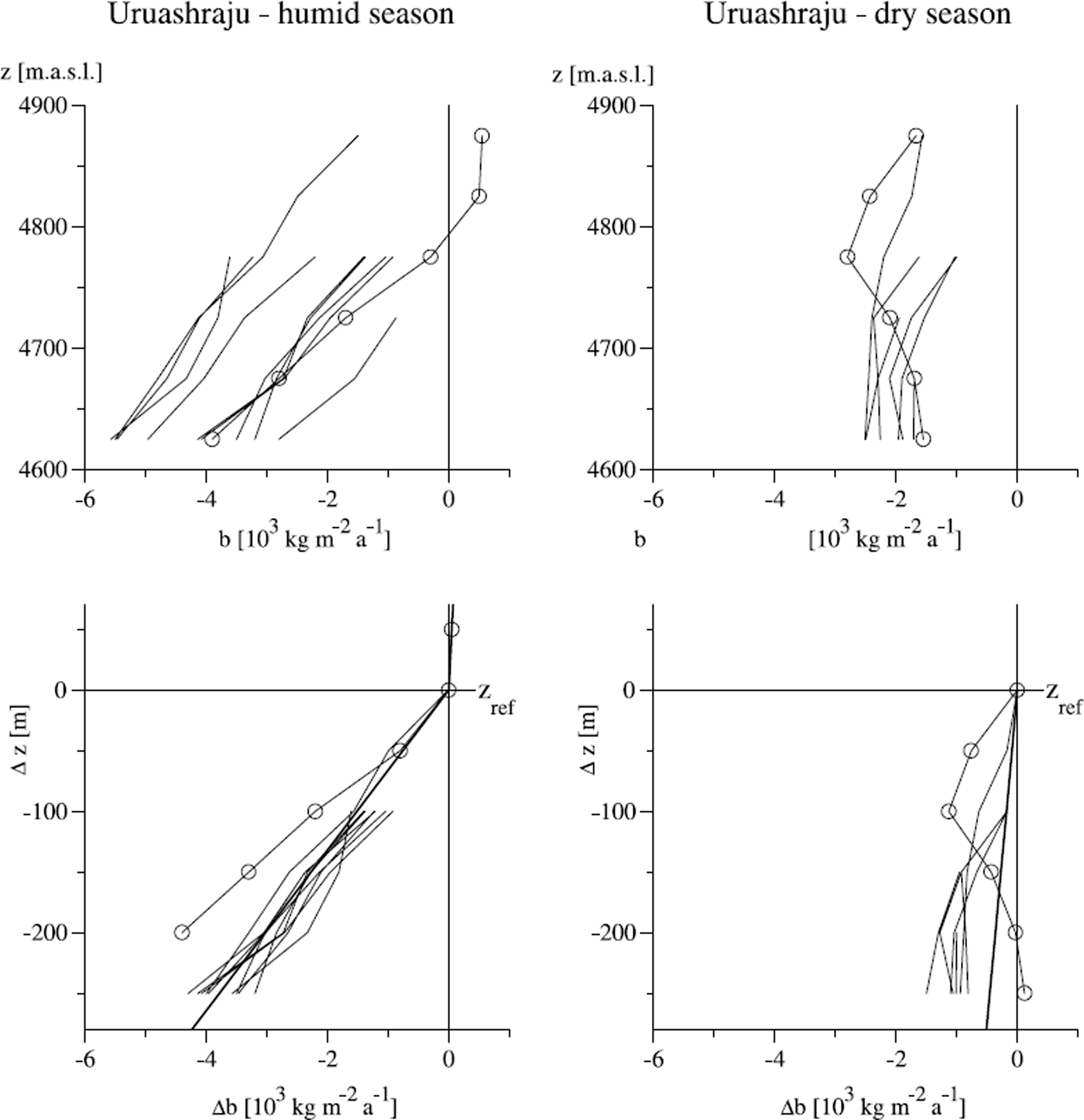
Fig. 5. VBPs, measured at Glaciar Uruashraju, and comparison with the modelled inner-tropical and subtropical profiles (bottom) for each season. Circles indicate the profiles in the 1982/83 El Niño year. Note that z ref is at the 0°C level for the humid season and is at the EL for the dry season. For detailed discussion see text.
Mass-balance measurements were carried out by members of the Peruvian hydropower company HIDRANDINA S.A. on Glaciar Uruashraju, southern Cordillera Blanca, to name one example, in the 1970s and 1980s. VBPs from both the humid and dry seasons are reported by Reference Kaser, Ames and ZamoraKaser and others (1990). These circumstances are typical for the outer tropics and are responsible for the basic conditions of the respective glacier regimes, as discussed above. Figure 5a shows the measured profiles for Glaciar Uruashraju for each season, and Figure 5b the same profiles but grouped together in order to compare them with the synthetic profiles. Measurements were made only on the tongue in most cases and never cover the entire glacier. With the exception of the 1982/83 El Niño year (open circles in Fig. 5), the modelled VBPs correspond well with the measured VBPs for both seasons. Even if the modelled VBP for the dry season seems to deviate from the measured ones at first glance, a closer look shows that the gradient is correct for most altitude zones. With minor deviations from the postulated conditions, well within the uncertainty in the data, the model can easily reproduce most of these measured profiles. In addition to these results, investigations by Reference Wagnon, Ribstein, Kaser and BertonWagnon and others (1999) carried out at the mean ELA on the outer-tropical Glaciar Zongo, strongly support the reliability of the model. They show that, of the energy-balance terms, only the latent-heat flux changes fundamentally with the season. Whereas it is minor during the humid season, it consumes almost the entire energy surplus from the radiation balance input during the dry season. Because the reaction of glaciers to changes in the climate variables varies seasonally, the respective lengths of the alternating seasons due to changes in both the geographical setting of the glacier and long-term climate fluctuations have an important impact on the glacier–climate relation in the outer tropics. The shorter one of the seasons becomes, the more the annual VBP adopts the other season’s character. Reference KullKull (1999) and Reference Kull and GrosjeanKull and Grosjean (2000) have shown that this concept is useful in investigating paleo-circulation patterns.
The 1982/83 El Niño year shows conspicuously different VBP profiles on Glaciar Uruashraju. The 1982/83 wet season is indicated by a distinctly stronger balance gradient all over the tongue, and the dry season shows an inverse balance profile with almost no gradients in the lowest parts and a relatively strong gradient in the higher part of the tongue. Reference WagnonWagnon (1999) examined the 1997/98 El Niño–Southern Oscillation (ENSO) event under outer-tropical conditions at the mean EL of Glaciar Zongo. During this El Niño year, the noticeably higher ablation was mainly due to: (1) low surface albedo during the wet season owing to markedly lower precipitation, and (2) almost non-existent sublimation because of high air humidity during the dry season. A. Ames from Huaraz, Peru (personal communication, 1999), reports also that precipitation fell exclusively as rain all over the glacier tongues in the Cordillera Blanca during the entire 1997/98 ENSO period. These observations indicate clearly different conditions during ENSO events when the “ideal” subtropical model assumptions must be modified. The impact of such ENSO conditions on the VBPs cannot be adequately explained without the support of further field measurements.
4. Sensitivity of EL to Climate Variations
In addition to the VBP, the ELA is the most suitable parameter for interpreting glacier responses to climate variations. Its sensitivity to climate variations depends on the gradients of the mass-balance terms at the respective altitudes. In order to study the sensitivity of the ELs under the different conditions, their mean positions in the respective VBPs must be determined. For the mid-latitudes, the example of Hintereisferner indicates that the EL is somewhat below the 0°C level of the ablation period and thus below z ref (data taken from Reference Kuhn, Kaser, Markl, Wagner and ScheiderKuhn and others (1979) indicate that the EL is about 120 m below the summer 0°C level). In the inner tropics, the EL lies clearly below the 0°C level (Reference KuhnKuhn, 1980; Reference Ohmura, Kasser and FunkOhmura and others, 1992). Thus, the gradient below z ref is decisive for EL sensitivity studies. This is different for the subtropics, where the EL is set equal to z ref as a model assumption. Still, at the EL ∂α/∂z= 0 m so only the accumulation gradient affects the shift of the ELA. Yet, for EL sensitivity studies in the subtropics the model is clearly overtaxed at this point since the inaccuracies of the model assumptions crucially influence the result. Both a different accumulation gradient and a possible, albeit small, ablation gradient above z ref would markedly change the sensitivity of the ELA. Consequently, this discussion will concern only the inner tropics for comparison with the mid-latitudes. The gradients in question can be obtained from the respective idealized model as follows:
for the mid-latitudes: db/dz = 7.4 kg m−2 m−1 (±5%) taken as a mean between z = −100 and z = −150 m.
for the inner tropics: db/dz = 24.5 kg m−2 m−1 (±5%) being constant at z = −.
A useful model for studying the sensitivity of the EL to climate variations, presented by Reference KuhnKuhn (1980, Reference Kuhn and Oerlemans1989), is based on the following relation: if δc and δQ are small changes, or perturbations, in accumulation and heat balance, these variations can be compensated through changes in Δh of the ELA along the vertical gradients of the respective variables:

Reference KuhnKuhn (1980, Reference Kuhn and Oerlemans1989) has discussed in detail the validity, the sensitivity and the possible relation between the variables in this type of model. If it is assumed that the altitudinal changes, ∂/∂z, of τ, G(1 − α), the longwave irradiance and latent heat can be omitted in the respective range of Δh, and if the allocation to melting and/or sublimation is provided again by the factor f, the equation becomes
Note that variations in the shortwave radiation balance can be caused by changes in either the albedo or the global radiation or both. This model allows examination of different climate variations as if each were solely responsible for an observed or reconstructed shift of the EL. In turn, a possible rise of the EL, caused by a postulated variation of a climate variable, can be calculated. For both the mid-latitude and the inner-tropical regimes, Table 3 shows the values of Δh caused by given climatic perturbations under the assumption that they each appear alone.
Table 3. The change in ELA (m) caused by given individual perturbations, which act alone

Compared with the mid-latitudes, the values depicted in Table 3 show that, in the humid inner tropics, the reaction of the EL to changes in accumulation is distinctly weaker, whereas the reaction to changes in net shortwave radiation and to changes in air temperature is higher. The values in Table 4 show how sensitively the model reacts if the input variables are each changed by 10%. (Note that for f the uncertainty is not 10% of the starting value, which would be 0 for the inner tropics, but 10% of the entire range. Thus this result is not necessarily comparable with that for the other uncertainties.) A 10% uncertainty in τ is quite unlikely for the inner tropics, so the effects that have most influence on the ELA are those resulting from uncertainties in the lapse rate for all model runs and for C S in the accumulation and radiation runs. Still, all are below 10%.
Table 4. Percentage of the modelled shift of the EL due to a 10% uncertainty of each input variable for different model runs. Note that the uncertainty off is 10% of its entire range

5. Summary and Conclusions
Glaciers in low latitudes are climate indicators in large-scale zonal regions: the inner tropics, the outer tropics and the subtropics. The low latitudes are defined by low thermal seasonality which leads to continuous ablation and a constant 0°C level during the whole year. These regions are also defined by the global circulation patterns of the ITG and the trade winds, including their seasonal oscillation, which cause distinct spatial and temporal differences in humidity. On the one hand, this leads to different durations and amounts of accumulation, and on the other, changing air humidity alters the ratio of melting and sublimation, and thus the way in which energy is used for ablation. Studies of glacier-climate interactions have to take these peculiarities of low-latitude climate regimes into account. They determine both the form of the VBP and the sensitivity of the ELA to climate variations.
The model presented herein allows analysis of the characteristic variables in the different climate regimes of the low latitudes. Compared with the mid-latitudes, the VBP in the inner tropics has a steeper gradient in the ablation zone and a marked change toward weak gradients above the 0°C level. The subtropical profile has a distinctly gentler gradient. The duration of the ablation season is the crucial variable that, when changed, causes the difference between the mid-latitude and the inner-tropical profiles, and the ratio of melting to sublimation, when changed, is that which causes the difference between the inner tropics and the subtropics. As a consequence of the respective mass-balance gradients, the sensitivity of the EL to climate variations is, compared with the mid-latitudes, generally weaker in the inner tropics. However, the model is overtaxed when applied to the ELA sensitivity in the subtropics.
In summary, the glaciers of the humid inner tropics are considered to be most sensitive to variations in air temperature, whereas those of the dry subtropics are most sensitive to changes in air humidity, not only in terms of accumulation, but even more so when the ratio of melting to sublimation is considered.
The outer tropics, where most low-latitude glaciers are situated, are a transitional zone where tropical climate dominates during the humid season and subtropical conditions prevail during the dry season. This is important for the interpretation of glacier fluctuations. At first glance, integrated over the entire year, the outer-tropical VBPs may seem similar to those of the mid-latitudes. Looking at the different seasons separately, however, it becomes obvious that glaciers in the outer tropics obey different rules. Since the duration and the intensity of the different seasons varies with distance from the inner tropics, with lee- and windward effects and with the grade of continentality, and also changes with the long-term fluctuations of the global atmospheric circulation patterns, it is important to consider these issues when analyzing glacier–climate interactions in the outer tropics.
Acknowledgements
I wish to thank C. Georges for his support during many discussions and with the preparation of the figures, and I am very grateful to M. Kuhn and two anonymous referees and the scientific editor R. LeB. Hooke for their constructive criticisms and suggestions. This research was supported by the Austrian Science Foundation (FWF) grant No. P13567-GEO.