Introduction
Mathematical models for realistic ice sheets are generally unsolvable by analytical methods due to the nonlinearity of the equations, the complex geometry of the domain and the boundary conditions. Exact solutions of the shallow-icesheet equation are one method of analysing properties of the shallow-ice approximation (SIA), which is known to exhibit reduced regularity (singular derivatives) around ice-sheet summits and margins, where conditions for shallowness are violated. Indeed, the need for verification of numerical models has motivated the development of exact solutions for a variety of simplified sets of geometries, physical conditions, approximations and boundary conditions.
In this paper, we investigate two features of the shallowice-sheet equation for flat beds in a case for which no exact solutions are known. The first concerns the existence and stability of solutions for mass balance linearly dependent on altitude (case 1 in ‘Numerical results’ section). The second concerns the marginal singularity, where vertical surface inclination and vanishing ice thickness may result in a non-vanishing or even unbounded basal shear stress (case 2).
Exact solutions of ice-sheet equations with different degrees of sophistication have been studied. Reference VialovVialov (1958) presented an isothermal steady state for constant accumulation. More realistic accumulation functions (Reference BuelerBueler, 2003) and time-dependent solutions, both isothermal and thermocoupled, were proposed by Reference HalfarHalfar (1981, Reference Halfar1983) and Reference Bueler, Lingle, Kallen-Brown, Covey and BowmanBueler and others (2005, Reference Bueler, Brown and Lingle2007). These solutions use the fact that the equation can be separated by variables if the accumulation is a function of the horizontal coordinate only, or if the accumulation function has a specific dependence on elevation and time, and when the resulting integrals can be solved analytically (Reference Greve and BlatterGreve and Blatter, 2009). If the accumulation is a more general function of the ice surface elevation, the equation is not straightforwardly separable and its solution requires at least a numerical ODE (ordinary differential equation) solver. Such quadrature can sometimes be considered ‘exact’ for verification purposes.
Solutions for mass-balance functions which increase with surface elevation have been studied to address the stability of ice sheets in a changing climate (Reference WeertmanWeertman, 1961). Reference BodvarssonBodvarsson (1955) addresses this question by constructing an exact solution for a plug flow driven purely by basal sliding, but neglecting any ice deformation. Numerical studies using such mass-balance functions are well known in the literature (e.g. Reference OerlemansOerlemans, 1981; Reference Van den Berg, van de Wal and OerlemansVan den Berg and others, 2006), but these studies fail to resolve the mathematical question of the existence of a solution of the continuum problem. Furthermore, all numerical studies of this question must accept large margin-approximation errors because of the singularity of the surface gradient at the margin (Reference Bueler, Lingle, Kallen-Brown, Covey and BowmanBueler and others, 2005).
Although an unlimited mass balance growing linearly with elevation is not particularly realistic, we analyse the problem in some detail to learn about the mathematical qualities of the problem. This paper aims to give a mathematical proof of the existence of solutions to this shallow-ice-sheet model. In our approach, the solution is a minimizer of an energy functional. The novelty of this result (cf. Reference Calvo, Díaz, Durany, Schiavi and VázquezCalvo and others, 2002; Reference Antontsev and de OliveiraAntontsev and de Oliveira, 2008) is that the source term (the mass balance) in the stationary shallow-ice-sheet equation depends on the unknown ice thickness.
The existence is proven only for fixed ice-sheet margins. Steady-state solutions are also obtained by numerical solution of the transient equation using the time-steps of the temporal evolution as a fixed-point iteration. Though uniqueness of the steady solution is not proven rigorously, all steady solutions found by numerical iteration yielded the same result, independent of the initial geometry.
Using similar arguments, we show the non-existence of a solution (minimizer) in the free-margin case. This non-existence result follows from the same elevation/accumulation feedback ‘instability’ identified in earlier literature (Reference BodvarssonBodvarsson, 1955; Reference WeertmanWeertman, 1961), but unlike those sources we show non-existence in a model which includes ice deformation and which uses a realistic mass balance (linearly dependent on altitude and not piecewise-constant).
Another feature observed in the shallow-ice-sheet solutions is unbounded surface inclination at the margins. This alone may not be unrealistic for advancing ice tongues or even steady termini. However, the basal shear stress in the SIA is unbounded at the margins for some solutions (e.g. the Vialov profile; Reference VialovVialov, 1958), or it takes a nonzero value in some other solutions (e.g. Reference BuelerBueler, 2003). Without longitudinal coupling, the basal value of the driving shear stress, which is proportional to the product of the local surface inclination and ice thickness, should vanish. Otherwise, a non-sliding terminus with vertical end point should be shearing and eventually become overhanging, which is not consistent with steady state.
In this paper we solve the shallow-ice-sheet equation with power-law-type sliding parameterization independently using two different numerical methods: (1) a finite-difference scheme to solve the time-dependent partial differential equation and (2) a numerical quadrature to solve the ODE for the steady state. The transient solution evolved into a steady state where the basal shear stress vanishes at an apparently vertical terminus.
We present the model in the next section and give the existence theorem in the ‘Mathematical analysis’ section. We then present the numerical methods and the results of numerical simulations. Details of the mathematical proofs and solutions are given in the appendices.
Governing Equations
We consider the evolution of an idealized two-dimensional ice sheet on a flat base, centred at the origin (Fig. 1). The ice domain is described by the ice-thickness function, H(x, t), at point x and time t:
where L > 0 limits the horizontal and T > 0 the vertical extent of the domain and ![]() denotes the set of positive real numbers. Obviously, the ice thickness, H, must be positive.
denotes the set of positive real numbers. Obviously, the ice thickness, H, must be positive.

Fig. 1. Idealized two-dimensional ice sheet.
Ice is considered to be a non-Newtonian fluid governed by Glen’s flow law (Reference GlenGlen, 1958). In the SIA, the horizontal component of the ice velocity is given by

where g is gravity, ρ is the density, ξ is a variable of integration and u b is the basal velocity. The rate factor, A, and the flow-law exponent, n > 1, represent the flow properties of ice and are assumed to be constant.
Sliding over a hard rough bed is mostly determined by the deformation of the ice across the roughness elements. Dimensional analysis and model calculations suggest that the mean basal velocity is then a power function of the basal shear stress with the same exponent, n, as in the flow law for ice (Reference WeertmanWeertman, 1957, Reference Weertman1964; Reference GudmundssonGudmundsson, 1997; Reference Greve and BlatterGreve and Blatter, 2009),
where τ b is the basal shear stress in the SIA,
and C ≥ 0 is here assumed to be constant. Combining Equations (2) and ( 3) yields
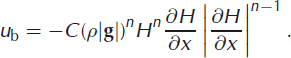
Consideration of mass continuity for a vertical column (Reference PatersonPaterson, 1994; Reference Picasso, Rappaz, Reist, Funk and BlatterPicasso and others, 2004) yields the Saint-Venant equation:

where b = b(x, z, t) is the accumulation (mass-balance) function. Combining Equations (1), ( 4) and ( 5) yields

with the two positive constants
where Γ is related to ice viscosity and ![]() to basal sliding.
to basal sliding.
Given the initial ice thickness function, H 0, the time-dependent problem consists of finding H such that:
The existence of and the uniqueness of the solution for the system of Equations (8– 11) has been investigated and proved by Reference Calvo, Díaz, Durany, Schiavi and VázquezCalvo and others (2002) for a mass balance which is independent of the altitude.
Mathematical Analysis
In this section we investigate the existence of stationary solutions if the mass balance, b, increases linearly with the altitude,
where a
m
> 0 is the vertical melt gradient and z
ELA
> 0 is the equilibrium-line altitude. The basal sliding is neglected, for now, by assuming C = 0. The stationary problem then consists of finding ![]() such that:
such that:
Here’ denotes the spatial derivative with respect to x.
Scaling
The previous problem is rewritten for the horizontal interval [−1, 1] with a scaling of H and x,
Equation (13) is reformulated in terms of ![]() and
and ![]() :
:
where’ now denotes the derivative with respect to ![]() . We transform Equation (16) into a p-Laplacian equation by applying a power transformation (Reference RaviartRaviart, 1970; Reference Calvo, Díaz, Durany, Schiavi and VázquezCalvo and others, 2002; Reference Antontsev and de OliveiraAntontsev and de Oliveira, 2008),
. We transform Equation (16) into a p-Laplacian equation by applying a power transformation (Reference RaviartRaviart, 1970; Reference Calvo, Díaz, Durany, Schiavi and VázquezCalvo and others, 2002; Reference Antontsev and de OliveiraAntontsev and de Oliveira, 2008),
which yields:
where

is a positive dimensionless coefficient. Finally, the problem of Equations (13–
15), reformulated in terms of η, consists of finding a function ![]() such that
such that
Equations (20– 22) form an obstacle problem which allows the solution to be identically zero on a subset of (−1, 1). In particular, the function vanishing on (−1, 1) is a trivial solution.
The goal of the next subsection is to prove the existence of a smooth function, η > 0, on (−1,1) satisfying Equations (20– 22). The existence of a strictly positive solution, H, of the original obstacle problem, Equations (13– 15), follows immediately by undoing the power transformation.
Existence of solutions with fixed margins
The existence of positive solutions to problems of the form
in (−1, 1), with boundary conditions η(−1) = η(1) = 0, where g is a sign-changing nonlinear term, has been the topic of recent publications, including Lü and others (Reference Lü, O’Regan and Agarwal2005). In our case p = n+ 1. The function ![]() defined as
defined as
and appearing in Equation (18), does not, however, satisfy the technical assumptions required in theorem 3.1 of Reference Lü, O’Regan and AgarwalLü and others (2005).
In what follows, we overcome this difficulty and prove the existence of strictly positive, even and radially decreasing solutions to the problem of Equations (20– 22) using the calculus of variations in theorem 2 (detailed below). Several steps are needed to reach this objective. In step 1, we consider an associated minimization problem and we prove the existence of a minimizer. In step 2, we show that the minimizer can be chosen even, radially decreasing and strictly positive on (−1, 1), as long as α is large enough. In step 3, we show that this minimizer solves the problem (Equations (20– 22)).
Throughout this subsection, we use Lp (−1, 1) to denote the space of all pth power Lebesgue-integrable functions on (−1, 1), and we denote by W 1,p (−1, 1) the space of all functions η ∊ Lp (−1, 1) admitting a weak derivative η’ in Lp (−1, 1) (Reference Lieb and LossLieb and Loss, 1997).
Step 1: minimization problem
From the point of view of the calculus of variations, any solution of Equation (18) is a stationary point (i.e. a point that makes the derivative zero) of a carefully chosen functional (Reference EvansEvans, 1999; Reference DacorognaDacorogna, 2008). The problem of Equations (20– 22) is then re-interpreted as a minimization problem, since any minimum is a stationary point. We will show this minimization problem has at least one solution, a global minimum. We cannot exclude that in some cases there are additional local minima, and possibly additional stationary points which are not local minima. The arbitrary choice of a minimum, versus a maximum, is guided by mathematical usage, since many physical problems can be rewritten in the form of an energy minimization.
In order to analyse the problem (Equations (20– 22)), we introduce the following functional space for our fixed-margin problem:
where p = n+1. Note that since p > 2 (n > 1), all functions of ![]() are continuous on [−1, 1] (e.g. Reference BrezisBrezis, 1999).
are continuous on [−1, 1] (e.g. Reference BrezisBrezis, 1999).
Since Equation (18) makes sense only where η is positive, we consider a convex subset, K, of ![]() , defined by
, defined by
We introduce the functional J, define on K,

where ![]() . The functional, J, is differentiable at any input, η, such that η > 0 on (−1, 1). Its derivative, 〈J’(η), φ〉, defined by
. The functional, J, is differentiable at any input, η, such that η > 0 on (−1, 1). Its derivative, 〈J’(η), φ〉, defined by
measures the infinitesimal variation of J at point η following the direction φ. A formal derivation of Equation (23) leads to

Note that
corresponds exactly to the weak formulation of Equation (18), with boundary conditions given by Equation (22), that is obtained by multiplying Equation (18) by an arbitrary test function, φ, and integrating by parts.
To prove the existence of a minimizer, the functional, J, needs to satisfy several mathematical properties, mainly coerciveness and convexity in the variable η’. Using standard arguments of convex analysis, using the convexity of the function ![]() , we are able to state the existence of a minimizer in the next theorem. The complete proof is given in Appendix A.
, we are able to state the existence of a minimizer in the next theorem. The complete proof is given in Appendix A.
Theorem 1
There exists at least one
![]() such that
such that
![]() for all η ∊ K.
for all η ∊ K.
Nevertheless, our understanding of the calculus of variations, including consideration of the arguments of Reference DacorognaDacorogna (2008), fails to resolve the uniqueness of ![]() because the function
because the function ![]() is not convex.
is not convex.
Step 2: properties of the minimizer
We formulate three lemmas stating the properties of the minimizer of theorem 1. They are proven in Appendix A. The first lemma shows that any minimizer of J in K may be chosen even and radially decreasing. More precisely, if ![]() is a minimizer of J in K, then we consider the even decreasing rearrangement (also called Schwarz symmetrization) η∗
of
is a minimizer of J in K, then we consider the even decreasing rearrangement (also called Schwarz symmetrization) η∗
of ![]() (Reference Lieb and LossLieb and Loss, 1997). The function η∗
remains in K and satisfies
(Reference Lieb and LossLieb and Loss, 1997). The function η∗
remains in K and satisfies ![]() . We deduce the following lemma.
. We deduce the following lemma.
Lemma 1 There exists an even and radially decreasing function on (0, 1) in the set K called η∗ such that J(η∗ ) ≤ J(η) for all η ∊ K.
The next lemma states that there exists η ∊ K such that J(η) < 0, as long as α is large enough. As a consequence, J(η∗ ) < 0 and η∗ is not the zero function.
Lemma 2 There exists α 0 ≥ 0 such that if α > α 0, then J(η∗ ) < 0, where η∗ is obtained in lemma 1.
The threshold, α 0, given in lemma 2, has the following physical meaning: the coefficient α, defined by Equation (19), needs to be sufficiently big (equivalently, L needs to be big enough, or z ELA small enough, or a m big enough) to guarantee the existence of a nonzero function, η∗ , and then the existence of a steady ice sheet. It should be stressed that α 0 depends on n but does not depend on L, z ELA, a m or Γ.
From these two lemmas, the function, η∗
is even, nonzero and decreasing on (0, 1). Let γ ∊ [0, 1] be the threshold, such that η∗
(x) > 0 for all x ∊ [0, γ) and η∗
(x) = 0 for all x ∊ [γ, 1]. The third lemma states that the scaled function ![]() of η∗
that belongs to K satisfies J(ζ) < J(η∗
) if γ < 1. As a consequence, γ is necessarily equal to 1 and η∗
> 0 on (−1, 1).
of η∗
that belongs to K satisfies J(ζ) < J(η∗
) if γ < 1. As a consequence, γ is necessarily equal to 1 and η∗
> 0 on (−1, 1).
Lemma 3 Let η∗ ∊ K be the even and radially decreasing function on (0, 1) obtained in lemma 1. Suppose that α > α 0, where α 0 is given in lemma 2. Then η∗ > 0 on (−1,1).
The first variation (Equation (24)) of J at point η∗ is now well defined, since η∗ > 0 on (−1, 1).
Step 3: back to problem, Equations (20– 22)
By using a first-variation argument, we are able to show that any minimizer of J which is strictly positive on (−1, 1) is a solution of Equations (20– 22) as long as α is large enough (see the proof in Appendix A). So we obtain the following result.
Theorem 2 There exists α 0 > 0 and for α > α 0 there exists a function η∗ ∊ K which is even, radially decreasing and strictly positive on (0, 1) satisfying Equations (20– 22). Moreover η∗ is continuously differentiable on [−1, 1].
By theorem 2, there exists a function
even, radially decreasing, strictly positive on (0, 1) and continuously differentiable on (−1, 1), that satisfies the original problem, Equations (13– 15).
Non-existence with free margins
The space ![]() used in the existence results above includes fixed-margin boundary conditions. Lemma 3 shows that if η(x) has its margin at γ < 1 then ‘advancing’ the margin to γ = 1 lowers the value of the functional, J, so the steady solutions found above are positive in (−1, 1) and also η(±1) = 0. These fixed-margin solutions correspond to ice sheets with nonzero flux at x = ±L, however.
used in the existence results above includes fixed-margin boundary conditions. Lemma 3 shows that if η(x) has its margin at γ < 1 then ‘advancing’ the margin to γ = 1 lowers the value of the functional, J, so the steady solutions found above are positive in (−1, 1) and also η(±1) = 0. These fixed-margin solutions correspond to ice sheets with nonzero flux at x = ±L, however.
Removing the fixed-margin boundary condition, η(±1) = 0, we consider η with arbitrary support in W
1,p
(−∞, ∞). Let ![]() : η ≥ 0 }. Also let
: η ≥ 0 }. Also let

which is the same functional extended to the whole real line. Then ![]() is unbounded below, by the following result (proved in Appendix A).
is unbounded below, by the following result (proved in Appendix A).
Lemma 4
There exists a sequence of even, radially decreasing functions, ![]() , each supported in a finite interval, so that
, each supported in a finite interval, so that
![]() .
.
Because the functional values for these profiles, ![]() , are exactly computable, and because these values are unboundedly negative, we know that there is no steady solution which could minimize
, are exactly computable, and because these values are unboundedly negative, we know that there is no steady solution which could minimize ![]() .
.
The ice sheets corresponding to ![]() can be compared to the states of a time-dependent solution undergoing runaway growth, in both horizontal and vertical extent. Such a time-dependent solution could grow by adding accumulation with increasing surface elevation, but at the same time flow would be insufficient to eliminate mass in the ablation area near the margin (cf. Reference WeertmanWeertman, 1961). By contrast, in the free-margin case with mass balance, b(x), depending only on horizontal position and with sufficient ablation outside a finite support accumulation interval so that
can be compared to the states of a time-dependent solution undergoing runaway growth, in both horizontal and vertical extent. Such a time-dependent solution could grow by adding accumulation with increasing surface elevation, but at the same time flow would be insufficient to eliminate mass in the ablation area near the margin (cf. Reference WeertmanWeertman, 1961). By contrast, in the free-margin case with mass balance, b(x), depending only on horizontal position and with sufficient ablation outside a finite support accumulation interval so that ![]() , the functional
, the functional ![]() would be bounded below.
would be bounded below.
Numerical Method
A simple way to obtain a numerical solution of the problem given by Equations (13– 15) is to implement that given by Equations (8– 11) and seek transient solutions converging into steady states. In this scheme, a time-step is one step in a fixed-point iteration scheme. Rewriting Equation (6) in the form

where

Equation (28) can be classified as a ‘nonlinear diffusion equation’, where D is the diffusivity. The nature of Equation (28) and the simplicity of the geometry suggests a finite-difference scheme on a uniform mesh be used in its solution. This problem has been widely investigated and several schemes have been proposed (Reference Huybrechts and PayneHuybrechts and others, 1996; Reference Van der VeenVan der Veen, 1999; Reference Bueler, Lingle, Kallen-Brown, Covey and BowmanBueler and others, 2005; Reference Van den Berg, van de Wal and OerlemansVan den Berg and others, 2006). The existing schemes can be characterized by two features. The first concerns the way to approximate the diffusivity, D, (Reference Huybrechts and PayneHuybrechts and others, 1996; Reference Van der VeenVan der Veen, 1999) while the second concerns the level of implicitness of the numerical scheme. We opt for an approximation of D at the midpoint of the discretization grid, based on centred mean ice thickness, H, and local surface derivative, ∂H/∂x. This choice corresponds to ‘type I’ described by Reference Huybrechts and PayneHuybrechts and others (1996). We use a semi-implicit time discretization of the diffusive part of Equation (28): ∂H/∂x is approximated at the current time while D is approximated at the previous time. In the case of an elevation-dependent mass balance (e.g. Equation (12)) b is updated at each time-step using the elevation at the previous time (Reference Van den Berg, van de Wal and OerlemansVan den Berg and others, 2006). Under appropriate stability conditions, this finite-difference scheme is locally order one accurate in time and order two accurate in space.
Numerical Results
In this section, we present two stationary solutions of the shallow-ice-sheet equation: case 1 for a mass balance linearly increasing with elevation and case 2 for an ice sheet with Weertman-type sliding.
Case 1: altitude-dependent mass balance
In case 1 we aim to find a numerical stationary strictly positive solution to the problem, Equations (13– 15), the existence of which has been proved in theorem 2. In all cases, the physical ice flow parameters are chosen as n = 3 and A = 3.17 × 10 − 24 Pa − 3 s − 1.
We use the mass-balance parameterization of Equation (12) with a m = 3.0 × 10−4 a − 1 and z ELA = 1000 m. Numerical tests are performed with three initial conditions:
-
(1)

-
(2)

-
(3)

where L = 1000 km. Ice is assumed to be fixed at the base, i.e. C = 0. The time-step is 1 year and the interval (−L, L) is discretized by 50 points.
By initializing the simulation with conditions 1 and 2, we check the uniqueness of the numerical solution (Fig. 2). Note that the shape stabilizes faster with initial condition 2 than with initial condition 1. Indeed, initial condition 1 is far from the steady solution, and the accumulation/ablation process needs ∼8000 years to reach a comparable volume to the steady shape. Initial condition 2 is closer to the solution in terms of volume, and the diffusion (which acts faster than the accumulation/ablation step) allows the stationary solution to be reached quickly. With the fluctuating initial condition 3, the diffusion becomes smooth quickly and passes through transient shapes, comparable to condition 1, to the same steady state. Several non-symmetric shapes were initialized (not shown); all resulted in the same symmetric steady-state shape.

Fig. 2. Experiments with different initial shapes: (a) initialization 1, (b) initialization 2 and (c) initialization 3. The time evolution of the ice thickness function is shown, with the initial shape as a continuous curve, the transient states as dotted curves and the steady state as a continuous curve with black dots.
Note that the stationary solution necessarily satisfies the boundary conditions implicit in lemma 3. Indeed the z-dependent mass balance induces a positive feedback of the solution in the source term of Equation (6). Runaway growth of the ice sheet occurs as L → ∞, i.e. with unlimited free margins.
The regularity of H is an important feature of the solution given by theorem 2. Figure 3 displays the numerical spatial derivative of the solution obtained with two different levels of resolution (100 and 400 points of discretization). For increasing resolution of the grid, the derivative converges to a continuous function, however, with a vertical asymptote at zero.

Fig. 3. Stationary thickness derivative function for two mesh resolutions, N = 100 and N = 400, where N is the number of points of discretization.
The time evolution of the functional, J, applied to time-dependent inputs ![]() , is shown in Figure 4. As expected, the functional, J, decreases and reaches a negative value at the limit, in accordance with lemma 2. Each initial function, H
0, must be chosen thick enough, otherwise the diffusion step could drive transient solutions below
z
ELA that would imply the inescapable collapse of the solution. The choice of a safe initial function has an interpretation in terms of the functional, J. Note that the zero function locally minimizes J. If the initial function is too close to zero, then the transient numerical solution, which minimizes J over time, converges to this local minimum and then fails to catch the global minimum.
, is shown in Figure 4. As expected, the functional, J, decreases and reaches a negative value at the limit, in accordance with lemma 2. Each initial function, H
0, must be chosen thick enough, otherwise the diffusion step could drive transient solutions below
z
ELA that would imply the inescapable collapse of the solution. The choice of a safe initial function has an interpretation in terms of the functional, J. Note that the zero function locally minimizes J. If the initial function is too close to zero, then the transient numerical solution, which minimizes J over time, converges to this local minimum and then fails to catch the global minimum.

Fig. 4. Time evolution of the functional, J, for each experiment corresponding to the initial shapes: 1, 2 and 3.
The particular choices of L, z ELA, a m, n and A fix the value of α (see Equation (19)). Since the numerical steady shape is positive, then α > α 0, where α is given in lemma 2. We are able to check the existence of this threshold. Indeed, by reducing L from 1000 to 100 km, we also reduce α. In this configuration, the stationary numerical solution vanishes everywhere on (−L, L) and the zero function is the minimum of J, which is consistent with lemma 2. An empirical value of α 0 can be estimated by repeating the calculation using various values of α. When n = 3, we find α 0 ∼ 147. The physical parameters L, z ELA, a m and A need to satisfy the inequality α > α 0 to ensure the existence of a nonzero steady shape.
This numerical evidence suggests the existence of the solution proved in theorem 2 and the uniqueness of this even, positive and radially decreasing steady shape. Note that the basal shear stress, τ b, of such a steady-state shape is not bounded and goes to infinity when x goes to the margins (Fig. 5).

Fig. 5. Basal shear stress, τ b, corresponding to the steady-state shape in case 1.
Case 2: altitude-independent mass balance and sliding
In case 2, a mass-balance function is chosen that does not depend on the unknown elevation of the ice sheet. This allows us to compute the location of the steady-state margin independently of the numerical solution of the ice-sheet shape. We choose a mass-balance function with constant accumulation in the inner part and constant ablation in the marginal part Reference Paterson(Paterson, 1994). The mass balance is defined by:

with a
1 = 5 m a
−
1, a
2 = −10 m a
−
1 and ![]() . The model domain extends to L = 1000 km. The steady-state margin is at x = 750 km, well inside the model domain.
. The model domain extends to L = 1000 km. The steady-state margin is at x = 750 km, well inside the model domain.
The stationary equation corresponding to Equation (6) can be integrated by numerical quadrature, up to a change of variable, which is a more accurate numerical scheme than the finite-difference ODE approach. Details, including a new power transformation to make a well-behaved ODE in the sliding case, are given in Appendix B.
In seeking to avoid such behaviour, basal sliding is introduced. With no sliding, the transient solutions converge to the steady-state solution of the stationary equation. They have non-vanishing basal shear stress at the margin (Reference Greve and BlatterGreve and Blatter, 2009).
The steady shapes are shown in Figure 6, both for vanishing sliding and for sliding with a coefficient ![]() . In contrast to case 1, the extent of the resulting steady-state ice sheet does not fill the given domain [−L, L] and the margin position matches the theoretical position accurately. Figure 7 shows the basal shear stress of the steady-state shape for both non-sliding and sliding ice sheets. For any sliding coefficient,
. In contrast to case 1, the extent of the resulting steady-state ice sheet does not fill the given domain [−L, L] and the margin position matches the theoretical position accurately. Figure 7 shows the basal shear stress of the steady-state shape for both non-sliding and sliding ice sheets. For any sliding coefficient, ![]() , the shear stress drops to zero at the margin.
, the shear stress drops to zero at the margin.

Fig. 6. Steady-state shape in case 2, without and with sliding.

Fig. 7. Basal shear stress, τ b, corresponding to the steady-state shape in case 2, without and with sliding.
Conclusions and Discussion
We have proven the existence of solutions of the stationary shallow-ice-sheet equation for a flat bed, vanishing sliding and fixed-margin position, in the case where the mass balance is a linear function of the unknown elevation. A change of variables allows us to rewrite the equation in the form of a p-Laplacian. Any minimizer of a corresponding functional, J, solves this equation. Using a symmetrization technique, the existence of an even, radially decreasing and strictly positive minimizer (solution) has been shown. Due to a lack of convexity, uniqueness of the solution needs to be investigated by a different approach. Essentially the same tools allow us to show the non-existence of solutions with free margin position. The interpretation of J as a system ‘energy’ is an aspect still to be investigated.
Removing the flat-bed or the non-sliding assumption changes the mathematical problem in a fundamental way. The power transformation, ![]() , used to transform the non-sliding flat-bed case of the SIA into a p-Laplacian problem (Reference RaviartRaviart, 1970; Reference Calvo, Díaz, Durany, Schiavi and VázquezCalvo and others, 2002) does not remove the double nonlinearity if the bed is not flat or if sliding is included. Further research is needed to resolve basic existence questions with sliding and/or non-flat bed, even in simpler cases where mass balance is independent of surface elevation.
, used to transform the non-sliding flat-bed case of the SIA into a p-Laplacian problem (Reference RaviartRaviart, 1970; Reference Calvo, Díaz, Durany, Schiavi and VázquezCalvo and others, 2002) does not remove the double nonlinearity if the bed is not flat or if sliding is included. Further research is needed to resolve basic existence questions with sliding and/or non-flat bed, even in simpler cases where mass balance is independent of surface elevation.
A finite-difference scheme for time-evolving solutions was used to find steady-state solutions numerically. The numerical experiments confirmed the theoretical results and suggested the existence of only one positive stable solution with fixed margins.
Similarly to the Vialov solution (Reference Greve and BlatterGreve and Blatter, 2009), the net mass balance is nonzero for fixed-margin solutions found here, and correspondingly the mass flux does not drop to zero at the margin. Thus the fixed-margin solution is not a steady-state solution for free-margin ice sheets. Runaway growth of the ice sheet occurs with free margins for large enough initial geometries. If the initial shape leads to a shrinking ice volume, no steady-state shape exists other than the zero solution. This shows the existence of an unstable equilibrium between runaway growth and runaway shrinkage.
The solution of the shallow-ice-sheet equation exhibits realistic physical conditions at the margin when Weertman type of sliding is included, in a case with accumulation only depending on the horizontal coordinate. Although the marginal surface still seems to have unbounded slope, the basal shear stress, and consequently the sliding velocity, vanish at the margin, giving conditions consistent with a steady-state geometry.
Acknowledgements
This work was funded by the Swiss National Science Foundation, project No. 200021-119721. E.B. received support from NASA grant NNX09AJ38G. We appreciate the comments of editor R. Greve, an anonymous reviewer and J. Bassis, all of which improved the paper and helped us place it properly in context.
Appendix A: Mathematical Proofs
Proof of theorem 1
Using the definition of J, the Hölder inequality, the Poincaré inequality and p > q, we can show there exists c 1 > 0 and c 2 > 0 such that:

for all η ∊ K. Since p > q > 1, the last inequality implies there exists c 3 > 0 and c 4 > 0 such that:

for all η ∊ K. Define
On one side, J(0) = 0, and on the other side, by Equation (A1), the functional J is bounded below. Thus ![]() is well defined. Let {ην} ⊂ K be a minimizing sequence for Equation (A2), i.e.
is well defined. Let {ην} ⊂ K be a minimizing sequence for Equation (A2), i.e. ![]() . There exists an integer, N, such that for all ν > N, we have
. There exists an integer, N, such that for all ν > N, we have ![]() . Using Equation (A1) and weak compactness, we can extract a subsequence, still denoted {ην
}, and find
. Using Equation (A1) and weak compactness, we can extract a subsequence, still denoted {ην
}, and find ![]() so that
so that ![]() in W
1,p
(−1, 1), weakly. Since K is strongly closed and convex, then K is weakly closed (see Reference BrezisBrezis, 1999). It follows that
in W
1,p
(−1, 1), weakly. Since K is strongly closed and convex, then K is weakly closed (see Reference BrezisBrezis, 1999). It follows that ![]() . Since p > 1, the function
. Since p > 1, the function ![]() is convex. Corollary 3.24 of Reference DacorognaDacorogna (2008) states the weak lower continuity of any functional,
is convex. Corollary 3.24 of Reference DacorognaDacorogna (2008) states the weak lower continuity of any functional, ![]() if f is continuous, ξ → f(u, ξ) is convex and if f satisfies f(u, ξ) ≥ c| u|r
, where
if f is continuous, ξ → f(u, ξ) is convex and if f satisfies f(u, ξ) ≥ c| u|r
, where ![]() , a < b and r ≥ 1. As an application of this result, we obtain that J is weakly lower semicontinuous. As a consequence,
, a < b and r ≥ 1. As an application of this result, we obtain that J is weakly lower semicontinuous. As a consequence,
Proof of lemma 1
Owing to theorem 1, we can consider a minimizer, ![]() , of J in K. Consider the even non-increasing rearrangement (or Schwarz symmetrization) η*
of
, of J in K. Consider the even non-increasing rearrangement (or Schwarz symmetrization) η*
of ![]() . (Reference Lieb and LossSee Lieb and Loss, 1997 for the definition; and the introduction of Reference BrockBrock, 2000 for relevant explanations.) The function η*
remains positive and equal to zero at −1 and 1. Moreover, η*
satisfies the property
. (Reference Lieb and LossSee Lieb and Loss, 1997 for the definition; and the introduction of Reference BrockBrock, 2000 for relevant explanations.) The function η*
remains positive and equal to zero at −1 and 1. Moreover, η*
satisfies the property

(Reference Lieb and LossLieb and Loss, 1997, p.73) and the property

( Reference Lieb and LossLieb and Loss, 1997, p.175). From Equations (A3) and
(A4), we deduce that ![]()
Proof of lemma 2
Consider the even function ![]() , which is in K. Recall that p = n + 1 >2 and
, which is in K. Recall that p = n + 1 >2 and ![]() . We have
. We have

where c 1 and c 2 are two positive constants. Clearly, J(η* ) ≤ J(η) < 0 if α is large enough.
Proof of lemma 3
It is easy to see that η* (0) > 0. Indeed, if η* (0) = 0, then η* would be equal to zero everywhere because η* is continuous, non-negative, non-increasing in (0,1) and η∗ (1) = 0. As a consequence, J(η∗ ) = 0 in contradiction to lemma 2. Define
We aim to show that γ = 1. Assume that γ < 1, and define ![]() . We are going to show that J(ζ) < J(η∗
)which is a contradiction with J(η∗
) = inf{J(η); η ∊ K}. Using the definition of J, the change of variable y = γx and the fact that η∗
= 0 outside (−γ, γ), we obtain
. We are going to show that J(ζ) < J(η∗
)which is a contradiction with J(η∗
) = inf{J(η); η ∊ K}. Using the definition of J, the change of variable y = γx and the fact that η∗
= 0 outside (−γ, γ), we obtain

Using ![]() and J(η∗
) < 0 (lemma 2), we obtain:
and J(η∗
) < 0 (lemma 2), we obtain:

Proof of theorem 2
Since η∗ is a minimizer of J in K then J[(1 − ∊)η∗ + ∊ξ)] = J[η∗ + ∊(ξ − η∗ )] ≥ J(η∗ ) for all ε ∊ (0, 1) and ξ ∊ K. It follows that
which becomes

Fix φ a smooth function with compact support. Then ξ = η∗ +τφ belongs to K if |τ| is sufficiently small because η∗ is continuous on [−1, 1] and η∗ > 0 on (−1, 1) by lemma 2. Thus Equation (A5) implies:

This inequality is valid for all sufficiently small τ, both positive and negative, and as a consequence

for all smooth functions, φ, with compact support. By definition of the weak derivative, it follows that |(η∗ )’|p −2(η∗ )’ ∊ W 1,1 (−1, 1) and
almost everywhere on (−1, 1). Since the functions of W 1,1(−1, 1) are continuous on [−1, 1], then (η∗ )’ is also continuous and η∗ is continuously differentiable.
Proof of lemma 4
Similarly to lemma 2, define a two-parameter family ![]() , with ηβ
,ℓ(x) = 0 if |x| ≥ ℓ. Recall
, with ηβ
,ℓ(x) = 0 if |x| ≥ ℓ. Recall ![]() is defined in Equation (27). A straightforward integration shows(A7)
is defined in Equation (27). A straightforward integration shows(A7)

Fix β > β 0 = [q(q + q)/2]1/(q−1), which depends only on n, so that 1 − 2βq− 1/[q(q + 1)] < 0. From Equation (A7)
can be considered a function of ℓ, with A, B > 0. Choose a sequence ℓ
k → ∞, define ![]() and note that
and note that ![]() because p > 1.
because p > 1.
Appendix B: The Steady-State Case with Sliding
Consider Equation (6) in the steady case with mass balance determined by horizontal location, namely the following ODE for H(x):
Suppose the choice of constants as in Equation (7), assume ![]() , and use the mass-balance function, b(x), given by Equation (30). As noted, it follows that the steady-state margin is at L
m = 750 km. The steady-state case we consider solves these conditions:
, and use the mass-balance function, b(x), given by Equation (30). As noted, it follows that the steady-state margin is at L
m = 750 km. The steady-state case we consider solves these conditions:
-
H(x) ≥ 0 for all x in (−L, L), and
-
if H(x) > 0 then H satisfies Equation (B1) at x.
This problem can be solved analytically up to a non-singular quadrature. We will convert the problem to a first-order ODE with a well-behaved right-hand side.
Because ![]() , however, a different scaling is appropriate relative to the choice in Equation (17) for a flat bed with no sliding. The correct scaling to de-singularize the margin is to replace H with
, however, a different scaling is appropriate relative to the choice in Equation (17) for a flat bed with no sliding. The correct scaling to de-singularize the margin is to replace H with
It is important to note that, unlike in the non-sliding flatbed case, the factor ![]() in the degenerate diffusivity,
in the degenerate diffusivity, ![]() , has a nonzero limit at the margin. In the new variable ω, Equation (B1) becomes
, has a nonzero limit at the margin. In the new variable ω, Equation (B1) becomes
where we have used the new exponent, r = n/(2 n + 1).
Symmetry implies that the flux at x = 0 is zero. In terms of ω, the flux is a constant multiple of ![]() . Integrating Equation (B3) therefore gives
. Integrating Equation (B3) therefore gives
where Q(x) is an odd (Q(−x) = Q(x)), continuous and piecewise-linear function satisfying
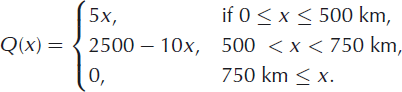
Symmetry considerations imply ω′ < 0 for x > 0, so the ice flow is in the positive x-direction for x > 0. Equation (B4) can be written
and the nth root computed:
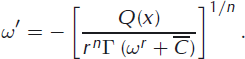
The initial condition is ω(L m) = 0.
Equation (B7) is of the form ω′ = f(x, ω). Because ![]() , the function f is Lipschitz in the dependent variable ω: there is λ independent of x so that |f(x,ω
2)−f(x,ω
1)| ≤ λ|ω
2
−ω
1
|. The derivative, ∂f/∂x, has a singularity at x = L
m, however. In fact, Q(x) ∼ (L
m − x) as
, the function f is Lipschitz in the dependent variable ω: there is λ independent of x so that |f(x,ω
2)−f(x,ω
1)| ≤ λ|ω
2
−ω
1
|. The derivative, ∂f/∂x, has a singularity at x = L
m, however. In fact, Q(x) ∼ (L
m − x) as ![]() so F(x, ω) ∼ (L
m
− x)1/n
as
so F(x, ω) ∼ (L
m
− x)1/n
as ![]() . This feature makes numerical solution by any means less accurate, but can be fixed by a transformation:
. This feature makes numerical solution by any means less accurate, but can be fixed by a transformation:
Let Ω(ξ) = ω(x) be the new dependent variable. Then

The initial condition is Ω(ξ) = 0 and we seek the solution on the interval ![]() . Equation (B8) is Lipschitz in the dependent variable Ω, and it is continuously differentiable in ξ at ξ = 0. This initial-value problem has a unique solution, and it is sufficiently regular to allow highly accurate numerical solution by an ODE solver. Figure 8 shows the solution produced by numerically integrating this initial-value problem, and compares it to the finite-difference solution obtained by solving the time-dependent problem and converging to steady state.
. Equation (B8) is Lipschitz in the dependent variable Ω, and it is continuously differentiable in ξ at ξ = 0. This initial-value problem has a unique solution, and it is sufficiently regular to allow highly accurate numerical solution by an ODE solver. Figure 8 shows the solution produced by numerically integrating this initial-value problem, and compares it to the finite-difference solution obtained by solving the time-dependent problem and converging to steady state.

Fig. 8. Case 2: stationary solutions with sliding (lower curve) and without sliding (higher curve) (cf. Fig. 6). The solution is obtained by two different methods: finite difference method (dotted) and numerical quadrature of an ODE (solid).










