Introduction
Recent work by Reference RöthlisbergerRöthlisberger (1968) and Reference Kamb, Kamb, Pollard and JohnsonKamb and others (1976) indicates that subglacial abrasion has a significant, perhaps dominant, role as the erosional process directly dissipating the basal sliding energy of temperate glaciers. The present study evaluates this hypothesis on the basis of a review of relevant aspects of glacial abrasion and sediment-transport hydraulics, measurements of sediment flux, and consideration of the gravitational energy balance of temperate glaciers. The importance of glacial abrasion in dissipating basal sliding energy appears confirmed, at least for Nisqually Glacier, Mount Rainier, Washington, U.S.A. (Fig. 1).

Fig. 1. Location map of the 1976 Nisqually Glacier terminus and the surrounding terrain. Contour interval is 10 m. Station A is the location of all water and suspended-sediment flux measurements at the terminus. Station B is the 400 m gaging, station plus summer and winter camp site. pH and carbonate-saturometer traverses were made between A and B, wherever snow and rock avalanches allowed access to the stream. Base map after map by courtesy of U.S.G.S. Glaciology Project Office and used by permission.
Subglacial abrasion measurements
Numerous workers have attempted to estimate the annual mass subglacially abraded by the indirect method of sampling suspended sediment and bed load in streams emerging from glacier termini (Klaeboe, 1951; Reference FahnestockFahnestock, 1963; Reference Arnborg, Arnborg, Walker and PeippoArnborg and others, 1967; Reference Østrem, Jopling and McDonaldØstrem, [c1975]; Reference CollinsCollins, 1979). Many assumptions are involved in extrapolating these measurements to give a figure for annual mass subglacially abraded; evaluation of their validity is attempted in the present study.
Assumptions and errors of method
It is assumed that all suspended sediment measured in the glacial stream is produced by subglacial abrasion. Fluvioglacial erosion during the study period is considered negligible due to comparative field observations during peak ablation and sediment transport. Although the glacial stream was an opaque, chocolate-brown color, a snow-melt stream with similar discharge but flowing over the steeper, western Nisqually Valley lateral moraines (Fig. 1) showed no significant turbidity and was used as drinking water. Both streams have opportunities for fluvial erosion over similar distances but only the heavily sediment-laden glacial stream flushes an environment where subglacial abrasion occurs.
Chemical dissolution of subglacially abraded mass prior to sampling at the terminus is considered negligible. Assuming similar size distributions for a laboratory-crushed and dissolved Nisqually Glacier sample and glacially abraded sediment, Reference Keller and ReesmanKeller and Reesman's (1963) chemical-weathering experiment indicates 0.03 weight % of rock is dissolved. Nisqually Glacier water has a calculated ionic strength of 10–4 and this purity is independently confirmed by specific conductances of 19 µmohs at 25°C in visually clear, spring run-off. Significantly, pH and carbonate-saturometer traverses established that subglacial waters, under-saturated with CO2, react to achieve equilibrium upon exiting the Nisqually Glacier terminus. (See also Reference Reynolds and JohnsonReynolds and Johnson (1971), Reference Stauffer and BernerStauffer and Berner (1978).) These results show that more dissolution can occur within 400 m of exiting a temperate glacier than beneath one, if the glacier bed is isolated from atmospheric CO2. Terminus sampling avoids this effect.
This study assumes all of the sediment annually eroded is essentially flushed out from under the glacier by the end of the summer melt season. Although there is significant evidence supporting the flushing hypothesis (Reference Østrem, Jopling and McDonaldØstrem, [c1975]; Reference CollinsCollins, 1979), there is evidence for water storage for periods of years in some glaciers, and one example is Nisqually Glacier (Reference RichardsonRichardson, 1968; Reference HodgeHodge, 1974). Assuming for non-surging glaciers subglacial abrasion is fairly constant over an interval of a few years, Reference Østrem, Jopling and McDonaldØstrem's ([c1975]) measurements give an estimate of 50% by weight for the annual variation from incomplete flushing of abraded sediment.
Usually about 40% of the total subglacial sediment load is carried as “bed load”, when measured at the terminus of some Norwegian glaciers (Reference Østrem, Jopling and McDonaldØstrem, [c1975], Reference Østrem1976). This study assumes fragments comprising the bed load are produced by other processes (such as plucking and quarrying) and that the “suspended load” is an order-of-magnitude approximation to the subglacially abraded mass.
There appears to be a seasonal variation in the detailed sediment-concentration-water-discharge relationships as different water and sediment sources are incorporated into the subglacial plumbing system during the winter-to-summer melt transition (Reference CollinsCollins, 1979). Integration of daily mass-flux measurements through time, when observations are lacking, can be a serious error if extraordinary, short-term releases of water and sediment are overlooked (Reference Østrem, Jopling and McDonaldØstrem, [c1975]; Reference CollinsCollins, 1979).
Water-discharge measurements made by stream gages can be grossly in error due to geologic changes in the stream cross-section and hydraulic jumps. Current-meter techniques or careful gage construction will overcome these problems (Reference CollinsCollins, 1978; Reference Anderton and ChinnAnderton and Chinn, 1978).
Water- and sediment-flux measurements varied by 2–5 times only 400 m down-stream from terminus observations. During constant water flux in early spring, down-stream measurements (at B in Figure 1) showed increased sediment flux from erosion of bed fines up-stream.
All previous studies assumed that one sample of suspended sediment suffices to calculate accurately sediment flux through a given cross-section. In winter this is correct, but that sediment is a negligible part of the annual load. In summer, lateral variations in suspended sediment concentration of 2–8 times were recorded within a 30 s interval at a given cross-section. Each sample of a section profile was taken in 5 s, so some time variation cannot be ruled out.
Method of measurements
Sediment-flux estimates were obtained by multiplying measurements of suspended-sediment concentration by those of water flux measured at the glacier terminus. Suspended-sediment samples were taken using the technique of Reference Østrem, Jopling and McDonaldØstrem ([c1975]), but with additional cross-stream samples characterizing lateral variation in different flow regimes. Water-flux measurements were made with a Price current meter and sounding rod, using the technique of Reference FahnestockFahnestock (1963). Mean water velocities were computed as 0.6 times surface velocities (Reference FahnestockFahnestock, 1963), mainly to reduce equipment damage from bed-load collisions during summer.
Observations
The winter of 1976–77 was an abnormally dry one for Mount Rainier. Less snow was available for run-off. During a similarly dry year (1959), Reference FahnestockFahnestock (1963) thought that substantial melt from the upper reaches of Mount Rainier was the cause of observed increases in water and sediment flux from Emmons Glacier, compared to the previous summer. If this was the case in the present study, the measured fluxes are greater than in “normal precipitation” years.
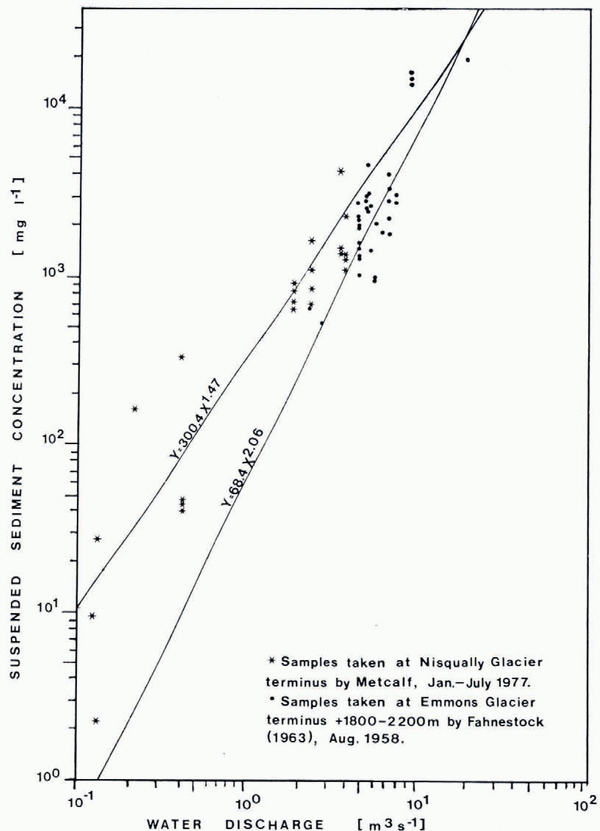
Table I shows the estimated yearly water and sediment fluxes from beneath the glacier. Included are both a daily averaged sediment flux and one derived from a least-squares power-law fit of suspended sediment concentration versus water discharge as shown in Figure 2. For the flux measurements in Table I, January through June represent field measurements at station A. The remaining six months were estimated from a monthly ratio of terminus to gaging station discharge compared to previous years' water-flux records taken solely at the U.S.G.S. gaging station, 1.8 km from the terminus (Fig. 1).
Table I. 1977 water and sediment fluxes from Nisqually Glacier, Mount Rainier, Washington


Fig. 2. Graph of the power-law relations for suspended-sediment concentration versus water discharge in two Mount Rainier rivers. Scatter for low discharge may be from time-dependent flushing of sediment from under Nisqually Glacier.
Early in the year (January through March), the subglacial sediment flux appeared to be increasing independently of discharge, as predicted by Reference Østrem, Jopling and McDonaldØstrem ([c1975]). The sediment transport during the entire month of January is equaled in 5 min in June! Although the power-law relation (γ = 300.4X 1.47 where γ is in mg l−1 and Χ in m3 s−1) had a much better correlation coefficient (r = 0.925) than those in the literature, the author believes this is probably due to relatively few concentration measurements being taken at a given water discharge. The more detailed sampling of Collins (1979) supports this interpretation.
Attrition grinding—the mechanism of subglacial abrasion
Attrition grinding is grinding by frictional wear. Attrition grinding appears to be the primary mechanism of subglacial abrasion. The friction generated during subglacial abrasion accounts for part of the basal shear stress at the rock–ice interface (Reference Kamb, Kamb, Pollard and JohnsonKamb and others, 1976).
Physics of attrition grinding
From watching cobblestone testing for wear resistance, Reference TroutonTrouton (1891) devised an alternative (to Mohs scale) measure of rock hardness, intrinsic to a given material. Reference TroutonTrouton (1895) defined this absolute coefficient of attrition grinding as the attritivity: “the amount removed per unit area, during unit displacement, when two surfaces of the same material undergo relative movement while pressed together with unit pressure”. Attritivity is commonly expressed in kilograms per joule.
The relative importance of plastic deformation and brittle fracture is critical to developing an effective model of subglacial abrasion. Commonly, rocks fracture to relieve high stress concentrations but Reference Westbrook and JorgensenWestbrook and Jorgensen (1965) have shown that many non-metals will deform plastically in micro-indentation experiments. In the first micro-indentation experiments with silicate minerals (load = 25 g, loading duration = 1 –1000 s, area of indentation = 20–35 µm2), Reference Scholz and EngelderScholz and Engelder (1976) demonstrated that plastic deformation was dominant.
Reference Bowden and TaborBowden and Tabor (1964, p. 320–64) suggested “that for extremely brittle materials the material will yield plastically without shattering only if the deformed region is smaller than a critical size”. By balancing normal forces on a rock abrading at the base of Nisqually Glacier and employing penetration hardnesses measured for quartz and olivine as an approximation to the mean value in andesitic rocks, one can calculate the fractional ratio of rock asperity area in contact at the grinding interface to the area of the rock in contact with the glacier above in order for plastic deformation to occur. At Nisqually Glacier, the effective pressure on a rock at the bed is ≈ 10 bar, but Reference Scholz and EngelderScholz and Engelder (1976) have shown that the effective pressure on a grinding silicate asperity must be at least 105 bar for plastic deformation to occur. The rock-asperity area actually in contact must be at least 10−4 times smaller than the rock-surface area under the pressure of the overlying glacier to undergo plastic deformation during subglacial abrasion.
In the only previous quantitative model of subglacial abrasion, Reference Boulton and CoatesBoulton ([c1974]) assumed that deformation occurs dominantly by plastic flow (Reference TaborTabor, 1954; Reference Bowden and TaborBowden and Tabor, 1964, p. 320–64). However, he did not show that plastic deformation actually is the dominant mode of attrition grinding beneath glaciers.
Laboratory tests of attrition grinding
Andesite from the Nisqually Glacier terminus was taken to the laboratory for attritivity tests similar to those of Reference Kamb, Kamb, Pollard and JohnsonKamb and others (1976). Boulders, 25–50 cm long, weighing 15–20 kg, were attached by 11 mm nylon rope to small spring scales. These scales crudely measured the static and dynamic coefficients of friction as one rock was pulled across another. Normal force equalled the weight of the top boulder. The comminution product was hand brushed from the interface after every pull of one boulder over another to avoid the lubrication effect seen by Reference TroutonTrouton (1895). All three boulders used had natural planar interfaces, picked in the field to provide stability during laboratory tests.
Sixteen runs established the attritivity of a boulder (minerals exhibiting a mean Mohs hardness of 6.5) over a boulder (exhibiting a mean Mohs hardness of 7.0) as 9 × 10−6 kg J−1. Enough runs were included to assure that the attritivity approached a constant value. No striations were visible after grinding. Instead, the apparent areas of contact looked similar to rough wood sanded with a medium sandpaper. About 90% by volume of the ground andesite appeared to have been created as semi-rectangular-shaped blocks (0.017–0.22 mm across) by brittle fracture, when observed by optical and scanning electron microscopes. The laboratory attritivity tests appear to have been dominated by brittle fracture, possibly due to the low confining pressures. This may yield an attritivity value that is not at all applicable to subglacial abrasion.
Field observations of subglacial abrasion
Subglacially abraded rocks and bedrock at Nisqually and Blue Glaciers were inspected to determine which mode of deformation dominates the abrasion process at the glacier base. Very smooth, continuous striations with small rock ridges along the groove edges appeared to represent plastic deformation. Chips and fractures in, and near, discontinuously grooved striations were taken as field evidence of brittle fracture. Two types of striation were observed: bas-relief and grooved depression. At Nisqually Glacier, the most common type consists of a plaster in bas-relief, commonly overlying a glacially polished surface which is previously undescribed in the literature. Sometimes, individual bas-relief striations extend for 40–60 cm on otherwise uniformly polished glacial boulders. On the other hand, the subglacial precipitates reported near Nisqually Glacier by Reference HalletHallet (1975) are usually an order of magnitude wider than a bas-relief striation and not more than 10–20 cm in length. The bas-relief striation is often grooved on its upper surface, contains some sand grains and in every case is the color of local rock softer than the stone it adheres to.
The other striation observed is the more familiar grooved depression (Reference ChamberlinChamberlin, 1888; Reference FlintFlint, [c 1971]). Many of the widest striations of this group (0.1–5.0 cm wide) have obvious fracture and prod marks (Reference ChamberlinChamberlin, 1888). Their association with crescentic gouges (Reference GilbertGilbert, 1906; Reference JohnsonJohnson, unpublished) adds support to the inference that the widest striations form dominantly by brittle fracture. The smaller striations (less than 0. 1 cm wide) in the grooved depression group appear to have been formed dominantly by plastic gouging based on the uniform continuity of unfractured grooves plus the raised ridges occasionally seen on the edges of freshly exposed (less than 20 years) striations.
Both grooved depression and bas-relief striations observed in the field appear to have exact counterparts in recent laboratory friction experiments of rock-on-rock sliding at velocities (10−4–10−3 mm s−1) and normal stresses on rocks at the bed (50-500 bar) similar to those believed to exist in the subglacial environment. Reference Engelder and ScholzEngelder and Scholz (1976) have shown that wear tracks in polished quartz are produced by an asperity harder than the underlying rock. The asperity ploughs a groove until shear stress exceeds the fracture strength of the asperity and it breaks off. These tracks of negative relief visually appear to be the same as grooved depression striations and may have formed in the same manner. Engelder and Scholz observed quartz wear tracks of positive relief caused by an asperity harder than the underlying rock rubbing off on the rock. The positive tracks appear to be the same as bas-relief striations and may have similar origins. Finally, when a quartz asperity slid over underlying rock of equal hardness, a track of fractures at high angles to the direction of slip was produced. These fractures may have similar origins to crescentic fractures and crescentic gouges observed in glaciated rock.
Theoretically derived attritivities
Details of this derivation are found in Reference MetcalfMetcalf (unpublished) and are omitted here due to space limitations. For Nisqually Glacier andesite and comparable materials, theoretical attritivities were calculated using the material properties of penetration hardness, elastic modulus, and fracture toughness. The attritivity derived using penetration hardness, associated with plastic deformation, gives the closest agreement (3 × 10−6 kg J−1) compared to the laboratory attritivities measured in the present study (1–9 × 10_6 kg J−1) and that of Reference Kamb, Kamb, Pollard and JohnsonKamb and others (1976) (3 × 10−6 kg J−1).
Paradoxically, experimentally abraded grains appeared in optical and SEM micrographs to be dominated by brittle fracture, not plastic deformation. Independent energy calculations by the author and N. W. Riley (written communication, 1978) suggest severe inefficiencies (such as crack propagation energy and frictional adhesion) exist, raising the energy expended in grinding by brittle fracture towards the value expected when plastic ploughing dominates. Thus, the observed good agreement between theoretical and experimental attritivities may not reflect the dominance of plastic deformation during abrasion but may prove valuable in empirical calculations of mass subglacially abraded.
Gravitational energy balance
In 1751, Altmann recognized that gravity was the cause of glacier motion (Reference PatersonPaterson, 1969), but no one has published acomplete gravitational energy balance for a temperate glacier. The importance of this exercise is to understand how much energy is available for glacier movement and subglacial abrasion.
The gravitational energy balance of a temperate glacier can be expressed as:
where E p is the change in gravitational potential energy in time interval (t), EI is the energy dissipated inside the glacier by viscous dissipation and other means, and Bs is the energy of basal sliding. This formulation inherently excludes any energy external to the balance of the mechanical movement of the glacier, including: heal input during internal water drainage (Reference ClarkeClarke, 1976), latent-heat loss by water run-off, heat input by surface and basal geothermal melting, plus the associated kinetic energy of surface and geothermal melt water and rain run-off. Energy dissipated by ice melting during subglacial abrasion is included in the Bs term.
The change in gravitational potential energy (Ep ) in a time interval (t) is given by:
where α is the mean slope of the glacier bed, t is the time interval of interest, (V s + V i) is the sum of mean sliding and internal velocities, g is the gravitational acceleration, pg is the mean density of the glacier, and I is the volume of ice under consideration.
The energy expended for internal deformation may be expressed as:
where Ab is the area of glacier bed and τi is the mean internal shear stress.
In like manner, the energy expenditure associated with basal sliding is:
where τb is the mean basal shear stress.
Employing the previously discussed assumption that all measured suspended sediment flushed from beneath the glacier is produced by subglacial abrasion, the energy expended in subglacial abrasion, E a, may be expressed as:
where M m is the measured mass eroded for the entire glacier. R is the ratio of bed area used in Equation (4) to the total bed area where basal drag occurs (for Nisqually Glacier, R = 1.96 km2/4.40 km2 = 0.45; this factor merely quantifies the fact that most sliding observations are accomplished over a fraction of the total glacier area), and At is the attritivity.
Three assumptions in this calculation are tenuous. Processes other than subglacial abrasion may produce rock flour from bedrock and not all of the subglacial bed is bedrock, so that energy requirements to produce the measured rock flour in suspension may be significantly different than calculated by attritivity theory. Any rock flour subglacially abraded but transported as bed load by Nisqually River is neglected. Secondly, it is not accurate to assume that bed abrasion is spacially uniform. There is probably less abrasion in the upper accumulation zone, where avalanched abrasive tools are in transit to the bed from above, and few may have been plucked from the bed. Finally, if the laboratory values for At are different than those at the glacier bed, the value for E a could be substantially in error.
In computing the gravitational energy balance, heavy reliance has been placed on the careful glacier dynamics studies of Reference HodgeHodge (1974, Reference Hodgeunpublished). Since Hodge's measurements are for lower Nisqually Glacier, the energy balance only includes the lower 2 km2 of the glacier. Ice depths were determined with a 20% accuracy by Hodge, using gravity methods. The fraction of the basal-sliding energy dissipated in subglacial abrasion, F in Equation (6), was estimated in the same manner as by Reference Kamb, Kamb, Pollard and JohnsonKamb and others (1976). It should be noted that the author believes their value of this fraction (0.29 for Blue Glacier) exhibits at least the range of errorcited for the present study (Table II).
Table II. Gravitational energy balance for lower Nisqually Glacier in one year (energy given in joules)

Subglacial abrasion models
Quantitative subglacial abrasion theory has only been recently developed by Reference RöthlisbergerRöthlisberger (1968), Reference Nye and MartinNye and Martin (1968), and Reference Boulton and CoatesBoulton ([C1974]). The reader is referred to Boulton's derivation as the only previous model “easily” tested by field observations.
For Nisqually Glacier (where V = 60 m a−1 and effective normal pressure is about 10 bar), Boulton's plot of theoretical abrasion-rates versus effective normal pressure for different ice velocities yields:

Beneath Icelandic glaciers with basaltic bedrock, Reference Boulton and CoatesBoulton ([c1974]) has empirically determined that  . Since there is no access to the predominantly andesitic bed of Nisqually Glacier, these Icelandic values were assumed to be the same at Nisqually Glacier, in order to test Boulton's model. Solving for the abrasion-rate, Ab* = 0.008-0.010 m a−1. This abrasion-rate multiplied by the mean density of Nisqually Glacier andesite (2.7 Mg m−3) and the area of the bed (4.4 × 106 m2) yields the annual mass abraded according to Boulton's model (108 kg a−1). Geologic mapping by the author shows that about 85% of Nisqually Glacier moves over andesite, and the rest moves over granodiorite near the terminus. This small area of granitic rock is considered to have no major effect on the mean abrasion-rates discussed in this study.
. Since there is no access to the predominantly andesitic bed of Nisqually Glacier, these Icelandic values were assumed to be the same at Nisqually Glacier, in order to test Boulton's model. Solving for the abrasion-rate, Ab* = 0.008-0.010 m a−1. This abrasion-rate multiplied by the mean density of Nisqually Glacier andesite (2.7 Mg m−3) and the area of the bed (4.4 × 106 m2) yields the annual mass abraded according to Boulton's model (108 kg a−1). Geologic mapping by the author shows that about 85% of Nisqually Glacier moves over andesite, and the rest moves over granodiorite near the terminus. This small area of granitic rock is considered to have no major effect on the mean abrasion-rates discussed in this study.
Boulton's model predicts 108 kg a−1 are abraded and the present study estimates 3 × 107kg a−1 are abraded. This discrepancy is within an order of magnitude; from the yearly variability (±50%), experimental error (less than 50%), and assumptions (unknown percentage error) inherent in the mass-flux measurements, this could be termed a successful prediction.
An alternative model of subglacial abrasion is here proposed that is just as accurate for predicting such erosion at Nisqually Glacier. Attritivity may be used to estimate the annual mass abraded by
where M A is the mass annually abraded, At is the attritivity, F is the fractional ratio of basal grinding energy to basal sliding energy, C is the fractional ratio of particle area in contact with bed area, and B s is the annual basal sliding energy evaluated over the area of the glacier bed.
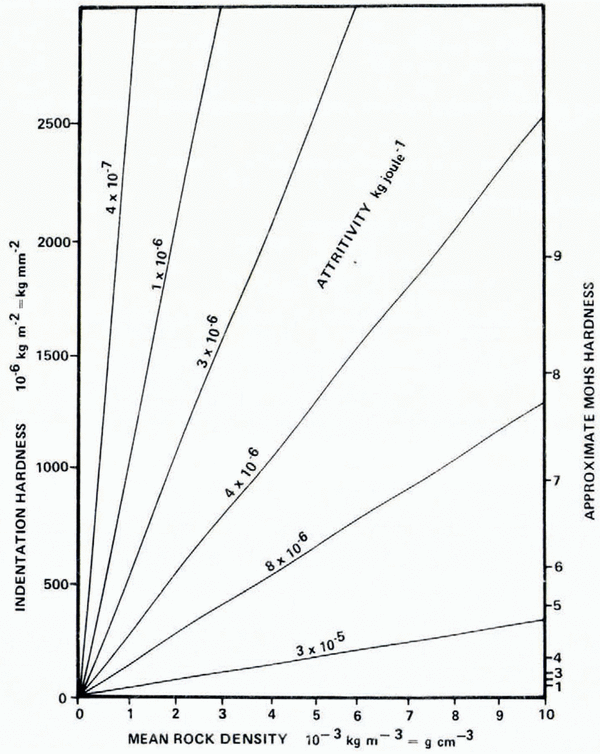
Attritivity dominated by plastic deformation may be theoretically calculated as the density of a given rock type, divided by the product of the indentation hardness and the gravitational acceleration. Since there is a physical relationship between Mohs hardness and indentation hardness (Reference Bowden and TaborBowden and Tabor, 1964, p. 347), attritivity may be calculated readily from the density and Mohs hardness of the bedrock (Fig. 3).
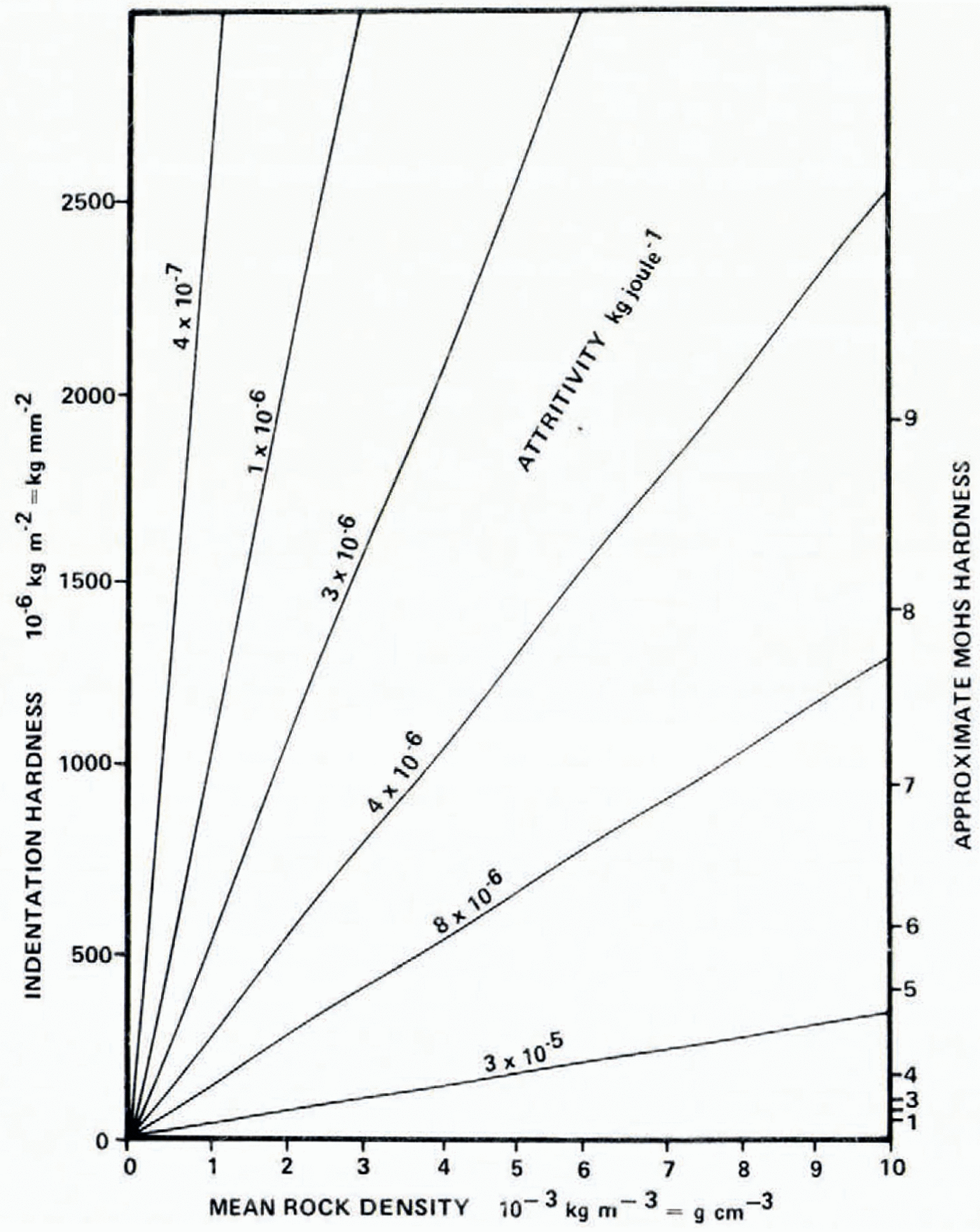
Fig. 3. Relaions between theoretically derived attritivity (based on assuming plastic deformation as the dominant mechanism in attrition grinding) and the physical properties (density and hardness) of the subglacial bedrock.
The best estimate for Nisqually Glacier of annual mass subglacially abraded is:
but, since the basal sliding energy is just that calculated by Reference HodgeHodge (1974) for the lower 45% of the glacier's basal area, the above value must be extrapolated (the assumed extrapolation is linear, although clearly basal sliding energy varies longitudinally through the glacier) by multiplying by 2.22 to yield 3 × 107 kg a−1, which is also the same figure given by field measurement. The maximum possible range of each variable is: At = 1 – 15 × 10−6 kg J−1, B s = 6.3 × 1012 – 2.4 × 1013 J a−1, F = unknown–1.00, and C = unknown–1.00. The estimated value for C was taken from Reference Boulton and CoatesBoulton's ([c1974]) subglacial observations and for F was based on using the maximum value of B s summed to E i to obtain the best agreement with Ep (Table II) in the gravitational energy balance. Exact agreement between calculated and measured abraded sediment was fortuitous, not intentional. Future work should concentrate on more rigorous measurements of C and F.
Table III. Comparison of production and characteristics of subglacially abraded mass at two north-west glaciers

Implications for future research
Analyses of glacier sliding ought to evaluate the importance of bed friction to sliding velocity through the basal shear stress. Reference ClappertonClapperton (1975) hypothesized that surging glaciers incorporate many more basal rocks by regelation refreezing into the glacier sole than comparable non-surging glaciers. More rock area traveling at a high velocity over the bed should increase subglacial abrasion compared to non-surge behavior. Increased subglacial abrasion should decrease basal sliding velocities by increasing the mean basal shear stress and tend to slow or stop a surge. These qualitative ideas should be developed into a glacier-sliding model testable by field observation.
Reference MorlandMorland (1976) has shown that a model of glacier sliding with friction, in which the tangential traction is proportional to a power of the slip velocity, will decrease the basal-sliding velocity by increasing bed friction. Reference Scholz and EngelderScholz and Engelder (1976) have demonstrated that during the striation of rock at approximate glacial sliding velocities (10−4–10−3 mm s−1) and normal stresses on rocks at the bed (50–500 bar), the shear stress is proportional to the log of sliding velocity. Future research should decide if the micro-scale striation-friction model of Scholz and Engelder actually controls the mega-scale glacier-bed friction model of Morland.
Budd (personal communication, 1978) has taken the first step by demonstrating that subglacial abrasion rates are proportional to the product of the basal shear stress, the effective normal pressure, and the sliding velocity to the one-third power. In Budd's experiments, he observed granitic rock abrading at 1 mm a−1 for 1 bar shear stress and 20 bar normal stress compared to andesitic rock at 2.5 mm a−1 for 1 bar shear stress and 10–12 bar normal stress at Nisqually Glacier.
Acknowledgement
E. R. LaChapelle, J. D. Smith, M. F. Meier, and R. V. Vivanco gave invaluable guidance. N. W. Riley and the Electron Optical Unit of the University of Newcastle-upon-Tyne provided numerous SEM photographs and X-ray fluorescence analyses of abraded grains. R. Stickney, J. Mitchell, and J. Mautz supplied winter field assistance in the face of considerable avalanche hazard. The U.S. National Park Service gave permission for the work at Mount Rainier and Olympic National Parks. This work was entirely supported by my own funds.
Discussion
D. N. Collins: Down-stream changes in solute content of melt water emerging from glacier portals suggest that waters of high solute content are added to the main stream in outwash areas from passage as ground-water morainic sediments beneath glaciers. Could this explain the changes you observed in the pro-glacial area of Nisqually Glacier?
R. C. Metcalf: First, one does not see damp moraine outside of the pro-glacial stream boundaries which would indicate a near-surface ground-water flow at Nisqually Glacier. Secondly, if the hydration of CO2 as melt water exits the terminus is the rate-controlling factor of observed pH changes, then one would expect that the distance of this change down-stream would be the product of stream velocity times the rate of the hydration reaction. This is precisely what I observed. However, I should point out that your hypothesis also precisely fits my field observations. Only future, presumably ingenious, research can resolve this problem.
G. S. Boulton: To what extent are your data capable of distinguishing between different erosional processes which may all be influenced in a similar way by changing glacier variables? For instance, I would expect an increase in glacier activity to result in increased abrasion, increased plucking, and increased fluvial erosion.
Metcalf: Fluvial origin of suspended sediment in the glacier stream was considered negligible in the Nisqually Glacier system for order-of-magnitude energy-balance computations. Microscopic examination of measured suspended sediments showed the universal blocky-grained morphology characteristic of grinding rather than rounded or highly angular fragments.
W. B. Kamb: The very high fine-particle turbidity of glacial outlet streams, by comparison with non-glacial streams of comparable size, shows that the fine particles in the glacial streams are derived mainly by glacial abrasion rather than fluvial transport.