Introduction
Ruth Glacier
Ruth Glacier is a 58 km long alpine glacier in the Alaska Range of central Alaska, USA (Fig. 1), residing in a sub-arctic continental climate (Reference Shulski and MogilShulski and Mogil, 2009) with a predominantly southern aspect. Ruth Glacier has a multi-lobed accumulation area consisting of a West Fork, Northwest Fork and North Fork. The headwall of the Northwest Fork reaches 4300 m a.s.l. and is ~ 4 km from the summit of Mount McKinley, the highest peak in North America. The separate lobes of the accumulation area converge at the head of the Great Gorge, a ~ 12 km long, 1.5–2 km wide valley with 1500 m high steep-sided walls that forms the upper ablation area between 12 km and 26 km (Fig. 1). In 1983 the ice depth in the Great Gorge was measured using seismic methods and found to be up to 1150 m thick (K. Echelmeyer, unpublished data). The lower ablation area, below the Great Gorge, is ~ 31 km long and 3–4 km wide and ends in a small piedmont lobe ~ 8 km wide, which is partially covered by vegetation. The average ice surface slope within the Great Gorge is 2.6ᵒ, and below the gorge the average ice surface slope is half as much, 1.3ᵒ, as indicated by the US National Elevation Dataset (Reference Gesch, Evans, Mauck, Hutchinson and CarswellGesch and others, 2009). At the base of the Great Gorge, there is some crevassing where the ice exits the gorge; the rest of the ablation area is free of major crevassing (as seen in the 30 m Landsat imagery used in this study), but the medial moraines exhibit a slightly wavy pattern. The Great Gorge, and parts of the West Fork, Northwest Fork and lower ablation area, are underlain by Tertiary (Paleocene) biotite-muscovite granite and quartz monzonite of the McKinley Sequence (delineated by the red polygons and denoted as Tpgr in Fig. 1) (Reference Reed and NelsonReed and Nelson, 1980; Reference Gamble, Reed, Richter and LanphereGamble and others, 2013). The North Fork and the ablation area immediately below the Great Gorge are underlain by sedimentary rocks from the Cretaceous and Jurassic periods (denoted as KJf in Fig. 1). These rocks are part of the Kahiltna Flysch Sequence and are composed of argillite, fine to coarse greywacke, conglomerates, and thin layers of chert and limestone (Reference Reed and NelsonReed and Nelson, 1980; Reference Csejtey, Mullen, Cox and StrickerCsejtey and others, 1992). Part of the piedmont lobe is underlain by Tertiary (Miocene) sedimentary bedrock composed of sandstone, siltstone, shale and claystone of the Tyonek Formation (delineated by the yellow dotted polygon and denoted as Tty in Fig. 1), which is part of the Kenai Group (Reference Solie, Gilbert, Harris, Kline, Liss and RobinsonSolie and others, 1991).
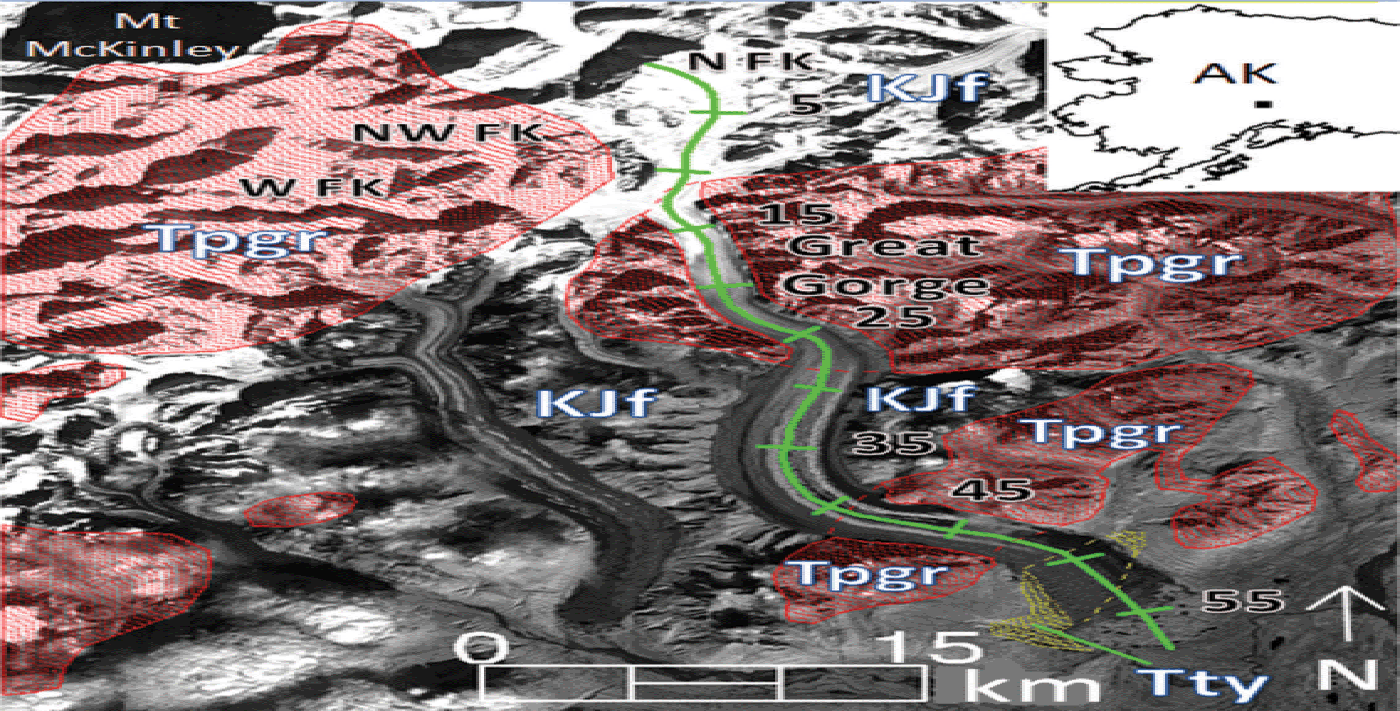
Fig. 1. View of Ruth Glacier, Alaska Range, Alaska. Red polygons indicate the extent of the granitic Tertiary age bedrock formations in the area, labeled Tpgr. KJf indicates Cretaceous/Jurassic age sedimentary bedrock, and Tty indicates Tertiary age sedimentary bedrock. The green line indicates a transect (km) along the glacier center line, beginning at the headwall of the North Fork. The background image was acquired by Landsat-5 TM on 9 September 1994. The black rectangle within the inset indicates the position of the background image within Alaska.
Little has been published concerning Ruth Glacier. Reference MayoMayo (1978) notes Ruth Glacier is a pulsing glacier and mentions the existence of small potholes in its surface that are the remnants of large crevasses. Reference Hall and OrmsbyHall and Ormsby (1983) examined Ruth Glacier using Landsat Multispectral Scanner (MSS) and Seasat synthetic aperture radar (SAR) data from the summer of 1978 and noted the firn zone was located within the Great Gorge. Reference Heid and KääbHeid and Kääb (2012a) produced velocity measurements for nine glaciers in the Alaska Range using optical feature-tracking methods and noted only Ruth Glacier had accelerated during the period 1986/87 to 2009/10; the zone of acceleration was restricted to the ablation zone below the Great Gorge. Reference Burgess, Forster and LarsenBurgess and others (2013) used SAR offset tracking to measure the wintertime speed of all glaciers in the Alaska Range during the late 2000s; the exact year is not given for each glacier, varying from 2007 to 2010. It was found that Ruth Glacier was moving at 0.6–1.0 m d–1 (219–365 m a–1) in the Great Gorge, with the ice gradually decelerating from ~ 0.5 m d–1 (182.5 m a–1) immediately below the Great Gorge to being stagnant at the terminus. Reference Ward, Anderson and HaeusslerWard and others (2012) note the igneous bedrock (Tpgr) of the Denali massif is significantly less fractured than the surrounding tectonically deformed sedimentary bedrock (KJf and Tty). Fracture spacing in the granitic bedrock is on the order of decimeters to hectometers, while fracture spacing in the sedimentary bedrock is on the order of centimeters to decimeters. This difference in fracture spacing causes a large difference in rates of glacier erosion (plucking) between the two predominant bedrock types. The result is that the valley in which Ruth Glacier resides tends to be narrow, with steep-sided walls (often 608 or greater in slope) in regions underlain by the granitic bedrock (e.g. the Great Gorge and between 41 and 48 km), and the valley tends to be wider with shallow-sloped walls (often 45ᵒ or less) when underlain by sedimentary bedrock (Reference Ward, Anderson and HaeusslerWard and others, 2012). Thus, the geometry of the glacier, and consequently ice thickness and basal shear stress, are dictated partly by the underlying bedrock type.
Pulsing glaciers
Reference MayoMayo (1978) defines glacier pulses as periodic unstable flow that is lesser in magnitude than surges, and pulsing glaciers are therefore intermediate between normal and surging glaciers. Pulsing glaciers may be identified by the existence of characteristic wavy medial moraines, large-scale wavy foliation, or boudinage that may be present on only part of the glacier, indicating only part of it pulses. If the characteristic pattern is continuous, it is suggested the glacier experiences regular, periodic pulses. Reference MayoMayo (1978) notes that potholes (remnants of crevasses) probably form in the zone of ice loss on pulsing glaciers. Approximately 140 glaciers in Alaska have been identified with these characteristics in aerial photography from the 1960s and 1970s by A. Post and L.R. Mayo. Most of these pulse-type glaciers occur in the same regions as surge-type glaciers, in the Alaska Range, Chugach Mountains, St Elias Mountains and Wrangell Mountains. Pulsing behavior may occur in conjunction with the drainage of large glacier-dammed lakes, suggesting a link between basal hydrology and pulsing flow. Reference MayoMayo (1978) lists some pulsing glaciers and the dates of their observed pulses: West Gakona Glacier (1949), Nizina Glacier (1961), Trident Glacier (1970, 1971), MacLaren Glacier (1971, 1972) and Tokositna Glacier (1971, 1972). Additionally, undated pulses are listed for Capps, Eureka, Hayes, Kahiltna, Miles, Ruth and Sanford glaciers and the West Branch of Sheridan Glacier.
Sometime between 1974 and 1977, Trapridge Glacier, Yukon, Canada, began a prolonged surge that lasted until 2005 (Reference Frappé and ClarkeFrappé and Clarke, 2007). During the surge a string of five 4 year pulses were detected from 1981 to 2002, with amplitudes of ~ 10 m a–1, a 33% increase in velocity. Trapridge Glacier is a polythermal glacier with temperate upper ice and subzero basal ice, and is underlain by a deformable, permeable till up to 10 m thick (Reference Blake, Clarke and GérinBlake and others, 1992; Reference StoneStone, 1993). Increased ice velocity during the surge, and by inference during the pulses, is attributed to sliding at the bed caused by failure of the basal till. Till failure reduces basal friction, and transfers stress laterally to the glacier margins, thereby producing an area of plug flow along the central portion of the glacier, allowing ice there to accelerate. During a similar time frame, from approximately 1980 to 2002, Black Rapids Glacier, a temperate glacier in the central Alaska Range (Reference Harrison, Mayo, Trabant, Weller and BowlingHarrison and others, 1975), experienced two consecutive 12 year pulses, with amplitudes of roughly 20–25 m a–1, representing velocity increases of 55–65% (Reference NolanNolan, 2003). Black Rapids Glacier is underlain by a till 5–7 m thick (Reference Nolan and EchelmeyerNolan and Echelmeyer, 1999), and it has been shown via borehole tiltmeter measurements that up to 70% of the ice velocity during the pulses was due to deformation within the till at depths >2 m below the ice/till interface (Reference Truffer, Harrison and EchelmeyerTruffer and others, 2000). Again, it was proposed that till failure reduced stresses in the center of the glacier and transferred them towards the margins. This process promotes increased basal motion along the glacier center line and increased ice deformation near the margins (Reference Truffer, Echelmeyer and HarrisonTruffer and others, 2001; Reference NolanNolan, 2003).
Ice dynamics influence the length, area and volume of a glacier. Changes in ice dynamics, therefore, necessarily result in changes in the geometry of a glacier, which in turn affects its mass balance. For example, pulses and surges may rapidly transfer ice to lower altitudes where it is subject to increased air temperature and ablation, thereby promoting a reduction in mass balance. Knowing that dynamic instabilities such as pulses and surges are intimately tied to the basal conditions of a glacier, an improved understanding of the relationship between basal conditions and ice dynamics will further our understanding of the influences on a glacier’s mass balance. In this study we examine the cyclical dynamic behavior of Ruth Glacier to determine the amplitude, frequency and spatial extent of its pulses. Based on the spatial and temporal structure of the velocity fields during multiple pulse cycles, we infer the basal conditions beneath Ruth Glacier and describe the influence of bedrock lithology on the behavior of its pulses.
Methods
Optical feature tracking
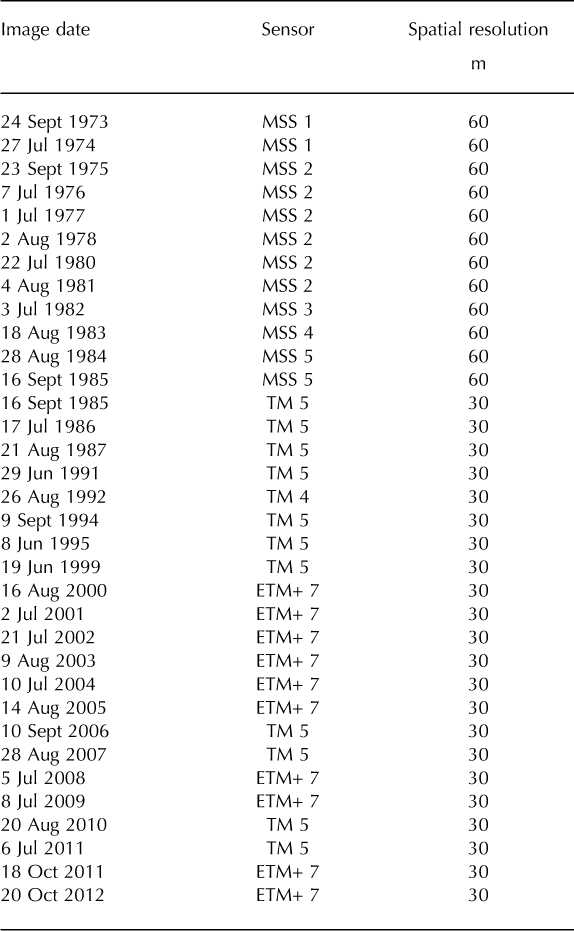
Optical feature-tracking methods were used to produce a time series of ice surface velocity maps spanning 1973–2012 for Ruth Glacier in order to delineate its periodic dynamic behavior. COSI-Corr feature-tracking software (Reference Leprince, Barbot, Ayoub and AvouacLeprince and others, 2007) was used in conjunction with 60 m Landsat MSS imagery and Thematic Mapper (TM) and Enhanced TM Plus (ETM+) imagery (30 m) to produce the velocity maps (see Table 1 for image dates). 30 m ETM+ imagery was chosen over 15 m panchromatic ETM+ imagery to be consistent with the 30 m spatial resolution of TM-4 and TM-5 imagery. COSI-Corr was chosen due to its proven precision (Reference Scherler, Leprince and StreckerScherler and others, 2008; Reference Heid and KääbHeid and Kääb, 2012b), its ability to produce accurate displacement measurements in areas of low contrast or with light cloud cover (Reference Heid and KääbHeid and Kääb, 2012b), and its ease of use. COSI-Corr produces an intitial estimate of the displacement of features between sequential images by use of the Fourier shift theorem which states the displacement is found in the phase portion of the normalized cross power spectrum computed from the Fourier transform of each image (Reference Shekarforoush, Berthod and ZerubiaShekarforoush and others, 1996). Equal-sized subsets from each image centered on the same pixel, called reference and search windows, corresponding to the temporally first and second images, respectively, are matched to one another, and a displacement measurement is produced with one-pixel accuracy. A reweighted least-squares phase minimization algorithm is then applied to determine the final displacement. This algorithm minimizes the phase difference between the initial displacement estimate and an ideal theoretical one, thus producing sub-pixel accuracy. The process is repeated in a grid-like pattern across the entire image, producing individual displacement measurements at predefined intervals. For this study, displacement measurements were produced every 16 or 32 pixels, depending upon the spatial resolution of the imagery. For 60 m MSS imagery a grid spacing of 16 pixels was used, and for 30 m TM and ETM+ imagery a grid spacing of 32 pixels was used. Both cases produce displacement measurements 960 m apart on the glacier. The displacement measurements (vectors) produced by COSI-Corr are post-processed using a neighborhood analysis routine to remove erroneous vectors. Any vector that is more than ± 2 standard deviations away from the mean magnitude or direction of its local neighborhood, consisting of at least nine adjacent vectors, is deemed an anomaly and removed. This filtering process is effective in removing isolated anomalies within a neighborhood of otherwise uniform vectors. Afterwards, the vector field is visually inspected and any remaining anomalies are manually removed. Manual deletion is necessary to remove clusters of anomalous vectors that might occur in areas of high velocity gradient, in cloud shadows or in areas with patchy snow cover. The remaining individual vectors are interpolated using a linear inverse-distance weighting scheme to produce a velocity raster. In May 2003, the scan-line correction mirror of Landsat-7 ETM+ failed, resulting in data voids in images acquired afterwards; these images are commonly called SLC-off images. Fortunately, the portion of Ruth Glacier in which the pulses are tracked (the ablation zone below the Great Gorge) lies near the center of the Landsat-7 images where the data voids do not exist. Therefore, methods that account for the data voids, such as Reference Ahn and HowatAhn and Howat’s (2011) null exclusion method or orientation correlation (Reference Fitch, Kadyrov, Christmas, Kittler, Marshall and RosinFitch and others, 2002; Reference Haug, Kääb and SkvarcaHaug and others, 2010), were not necessary when using SLC-off images for Ruth Glacier.
Table 1. Landsat images used in this study. Upon receipt from the USGS, Multispectral Scanner System (MSS) images have a spatial resolution of 60 m, and the Thematic Mapper (TM) and Enhanced TM Plus (ETM+) images have spatial resolutions of 30 m
Accuracy
The accuracy of the velocity fields produced from feature-tracking algorithms depends on the precision of the matching method and how well the two images being matched are aligned to one another. Reference Heid and KääbHeid and Kääb (2012b) evaluated the precision of COSI-Corr using Landsat-7 ETM+ 15 m panchromatic imagery and found the root-mean-square error (RMSE) of its displacement measurements to be ± 0.9 m in the x direction and ± 0.8 m in the y direction, for a total RMSE of ± 1.2 m, or ± 0.08 pixels. If we apply this same error (± 0.08 pixels) to 30 m imagery, the expected error is ± 2.4 m, and for 60 m imagery the expected error is ± 4.8 m. Reference Storey and ChoateStorey and Choate (2004) have shown the RMSE of the geometric accuracy of Landsat-5 TM data is ± 5.5 m (± 0.2 pixels), and Reference Lee, Storey, Choate and HayesLee and others (2004) showed the average geometric error of Landsat-7 ETM+ imagery is less than ± 5 m (± 0.166 pixels). Table 2 (last column) shows the listed geometric accuracy for each Landsat image used in this study, upon receipt from the US Geological Survey (USGS); the mean of the 22 values for TM/ETM+ images is 0.16 ± 0.04 pixels (4.8 ± 1.2 m) (mean ± 1 standard deviation), which compares well with the values given by Reference Storey and ChoateStorey and Choate (2004) and Reference Lee, Storey, Choate and HayesLee and others (2004). For the 12 MSS images, the mean geometric error is 0.47 ± 0.12 pixels (28.2 ± 7.2 m).
Table 2. Georeferencing error and residual error for each image pair used to produce velocity fields. Georeferencing error represents the initial misalignment between the two satellite images as measured using COSI-Corr, and the residual error represents their misalignment after the georeferencing error is removed. Image geolocation RMSE is the root-mean-square error of the geometric misalignment of each image with respect to ground control points, as determined during processing of the images before distribution to the public domain. Values given are mean ± 1 standard deviation
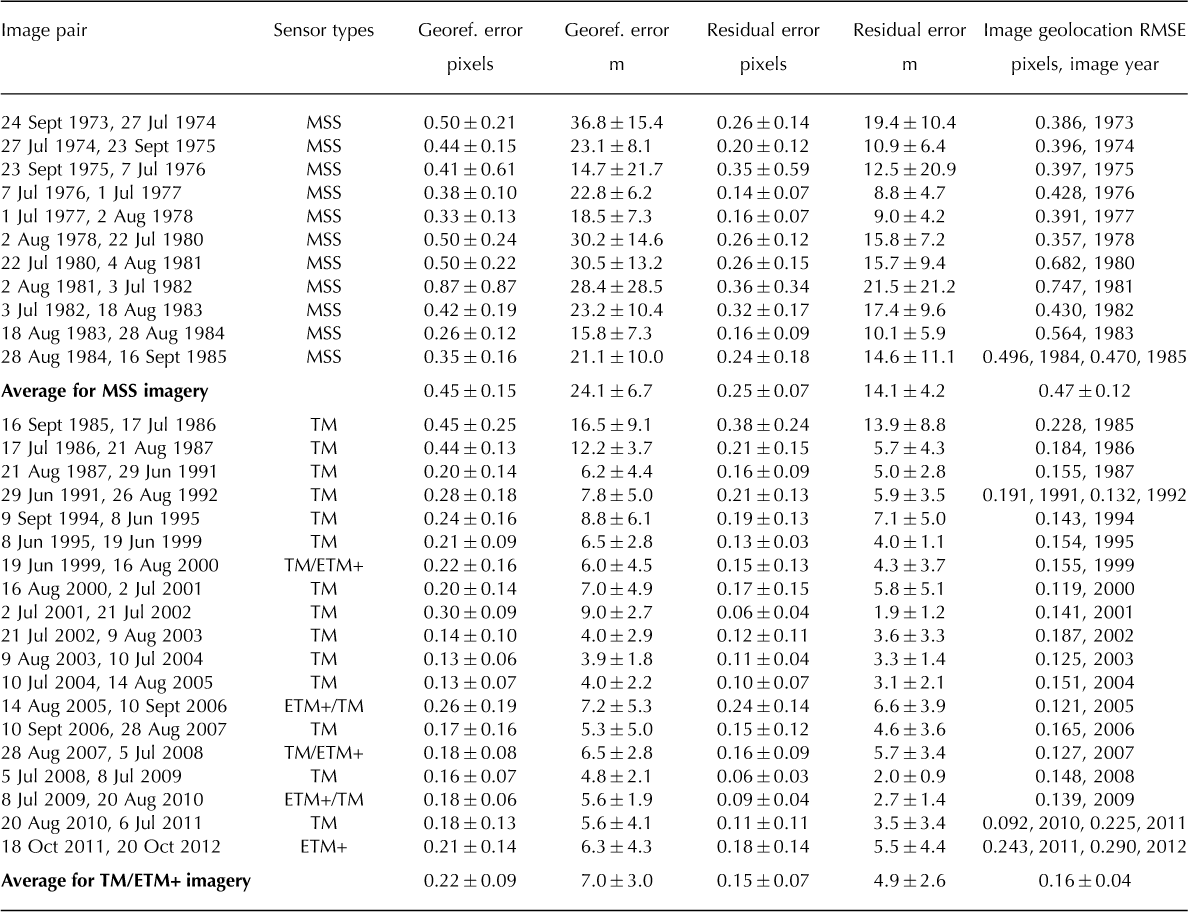
For each image pair, vectors on dry, snow-free, cloud-free land were analyzed to determine the mean georeferencing error between the two images (Table 2). The average of these mean georeferencing errors is 0.22 ± 0.09 pixels (7.0 ± 3.0 m) for 30 m TM and ETM+ imagery and 0.45 ± 0.15 pixels (24.1 ± 6.7 m) for MSS imagery. The mean georeferencing error for each image pair was subtracted from the on-ice vectors to improve the accuracy of the velocity fields. The mean georeferencing error was also subtracted from the off-ice vectors, resulting in a residual error between images which represents their final misalignment (Table 2). We note the average of the mean residual errors for the TM/ETM+ image pairs, 0.15 ± 0.07 pixels (4.9 ± 2.6 m), compares well with values quoted above by Reference Storey and ChoateStorey and Choate (2004) and Reference Lee, Storey, Choate and HayesLee and others (2004), and with the mean geometric accuracy for an individual image. Thus, after removal of the mean georeferencing error, the TM/ETM+ image pairs are aligned to one another as precisely as each individual image is aligned to the ground control points used to geolocate it. We also note the image-to-image misalignment for each TM/ETM+ image pair is within one standard deviation of the precision of COSI-Corr (± 0.08 pixels), which suggests that after removal of the mean georeferencing error the residual misalignment of the TM and ETM+ image pairs approaches the limits of detection by COSI-Corr. The mean georeferencing error for MSS data, as measured by COSICorr (Table 2), is 0.45 ± 0.15 pixels (24.1 ± 6.7 m), and after removal of this error, the residual image-to-image misalignment is 0.25 ± 0.07 pixels (14.1 ± 4.2 m). Thus, after removal of the georeferencing error, the MSS image pairs are aligned more precisely to one another than each individual image was originally aligned to its ground control points upon receipt from the USGS (compare the average residual error of 0.25 pixels to the average geolocation error of 0.47 pixels). Using the root-sum-of-squares method, we estimate the combined error in the velocity fields, resulting from the mean residual error and COSI-Corr’s precision, to be 5.1 m (0.17 pixels) for the 30 m Landsat TM/ETM+ data, and 15.7 m (0.26 pixels) for the 60 m Landsat MSS data.
Results
COSI-Corr was unsuccessful in producing reliable displacement measurements within the Great Gorge and in the accumulation area due to snow cover and a lack of surface features to track, but it was successful below the Great Gorge. A time series of 29 velocity maps (Figs 2–5) shows the evolution of the pulses of Ruth Glacier in time and space, below the Great Gorge. From 1973/74 to 1976/77 (Fig. 2a–c) much of the ablation area below the Great Gorge moves at 75 m a–1 or less. Then in 1977/78 (Fig. 2d) the ice down to 30 km accelerates to almost 200 m a–1. In 1978–80 (Fig. 2e) the ice between 35 and 40 km has accelerated relative to previous years, and by 1980/81 (Fig. 2f) all the ice down to 45 km has accelerated, much of it moving 150 m a–1 or more, indicating a doubling of ice velocity compared to the period 1973–77. From 1981/82 (Fig. 2g) to 1983/84 (Fig. 3a), the glacier gradually decelerates and returns to its pre-pulse velocity. In Figure 3 there are two pulses evident between 1984/85 and 1995–99 that show a similar pattern of gradual acceleration and deceleration of the ice, with peak velocities in 1987–91 (Fig. 3e) and 1995–99 (Fig. 3h). Due to lack of cloud-free imagery between 1987 and 1991, and lack of data acquisition during the late 1990s, these pulses are not well defined in time, but it is clear the two pulses did occur due to the increased velocities during these 4 year time spans. From 1999/2000 to 2001/02 (Fig. 4) the cyclical pattern has continued, with a gradual increase in velocity from roughly 50–75 m a–1 in 1999/2000 (Fig. 4a) to >100 m a–1 in 2001/02 (Fig. 4c) between 26 and 35 km. By 2002/03 (Fig. 4d), velocity reached a peak, with characteristic values of 150– 200 m a–1 between 26 and 42 km, indicating the ice has more than doubled its speed compared to 3 years earlier. Afterwards, the ice decelerates to its pre-pulse velocity by 2005/06 (Fig. 4g). A fifth pulse is evident in Figure 5, which shows an acceleration of the ice from 2006/07 (Fig. 5a) to 2009/10 (Fig. 5d), with the peak being in 2009/10, followed by deceleration in 2010/11 and 2011/12 (Fig. 5e and f). Characteristic peak ice velocities during this last pulse, between 26 and 42 km, are 150–200 m a–1, indicating a three- to fourfold increase in velocity compared to 2006/07.
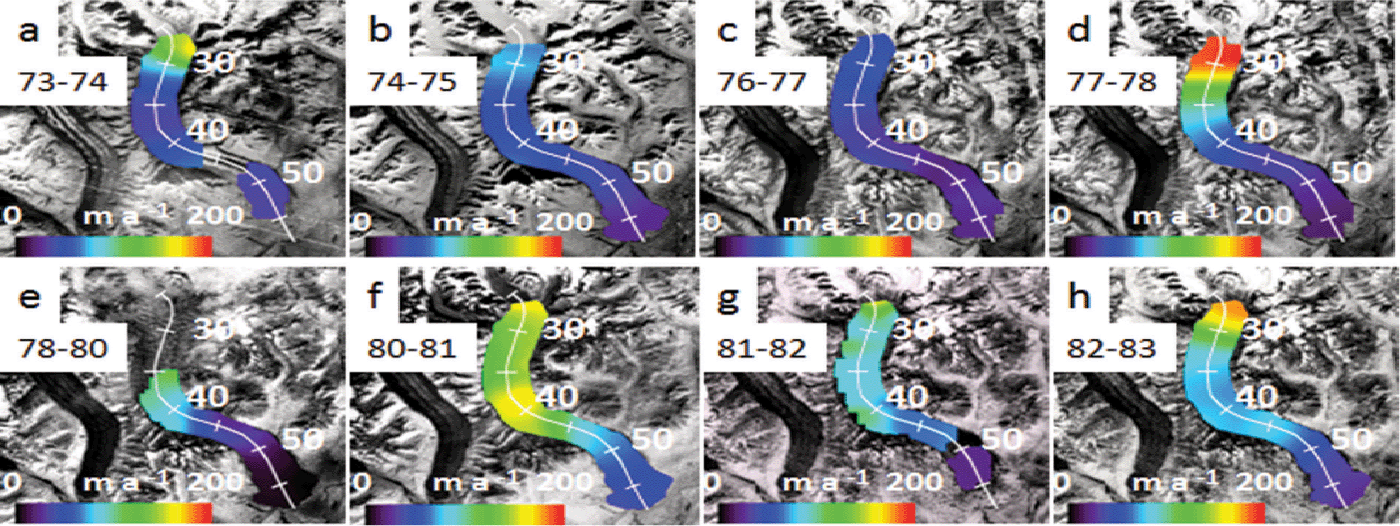
Fig. 2. Velocity fields for Ruth Glacier, below the Great Gorge, from 1973 to 1983. Distances (km) along the center-line transect are from the headwall of the North Fork (see Fig. 1). (a) 1973/74, (b) 1974/75, (c) 1976/77, (d) 1977/78, (e) 1978/80, (f) 1980/81, (g) 1981/82 and (h) 1982/83.
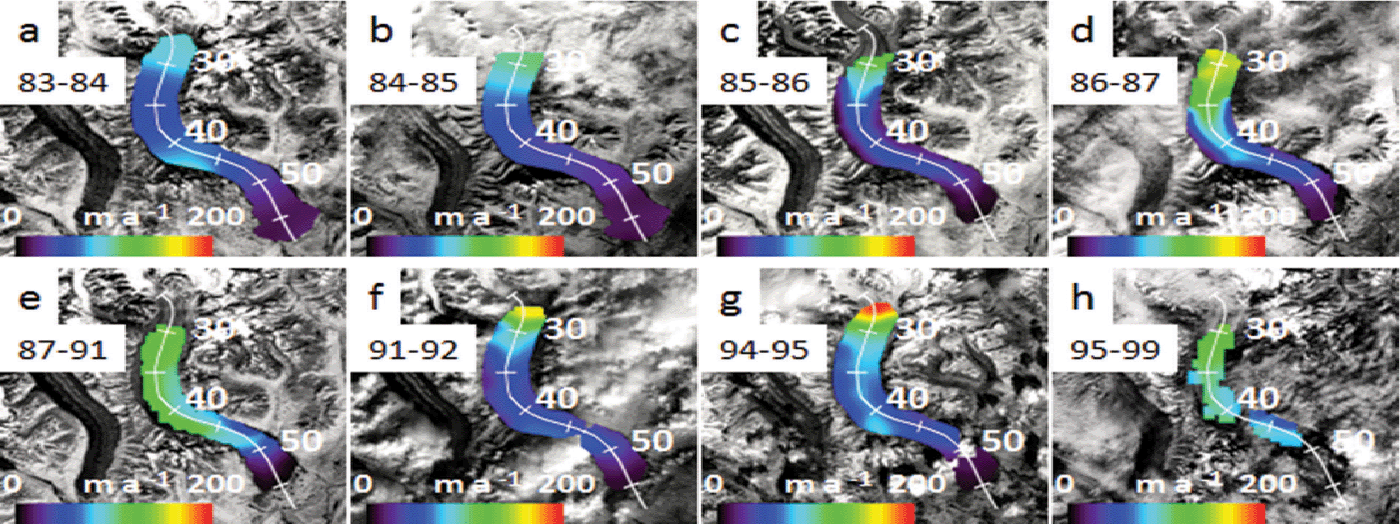
Fig. 3. Same as Figure 2, but from 1983 to 1999. (a) 1983/84, (b) 1984/85, (c) 1985/86, (d) 1986/87, (e) 1987–91, (f) 1991/92, (g) 1994/95 and (h) 1995–99.
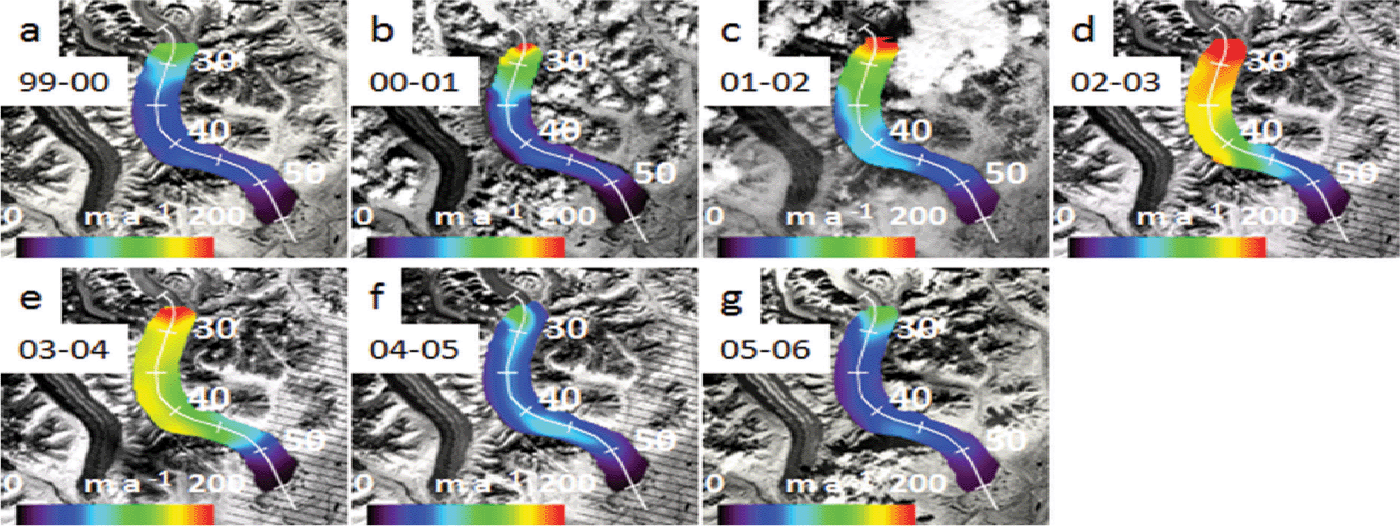
Fig. 4. Same as Figure 2, but from 1999 to 2006. (a) 1999/2000, (b) 2000/01, (c) 2001/02, (d) 2002/03, (e) 2003/04, (f) 2004/05 and (g) 2005/06.
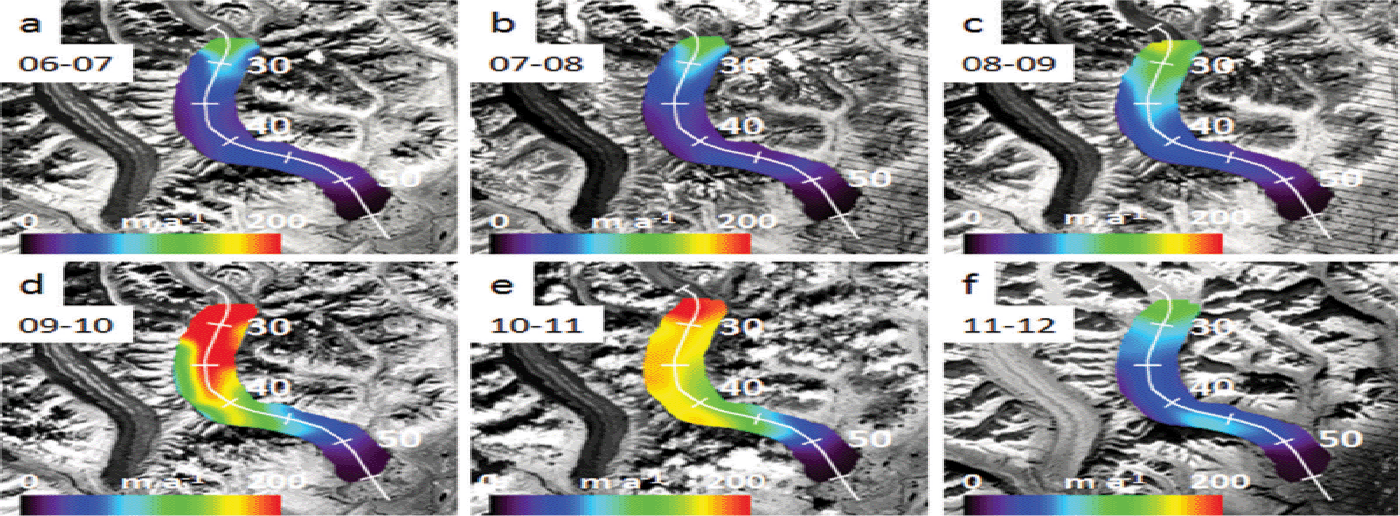
Fig. 5. Same as Figure 2, but from 2006 to 2012. (a) 2006/07, (b) 2007/08, (c) 2008/09, (d) 2009/10, (e) 2010/11 and (f) 2011/12.
To help illustrate the evolution of the pulses through time, the velocity at two points along the glacier, 36 km and 43 km, are plotted in Figure 6. This graph clearly illustrates the periodic nature of the pulses and highlights the five individual peaks. It should be noted that for plotting purposes, velocity was assigned to the second year of each image pair used to produce a velocity field, or in the case of the 1987–91 and 1995–99 velocity fields, velocity was assigned to a middle year, 1989 and 1997, respectively. Inspection of this graph yields characteristic pulse amplitudes (peak value minus trough value) in excess of 120 m a–1 (a 300% increase in velocity) at 36 km, and 60–70 m a–1 (a 50–75% increase in velocity) at 43 km for the 1981, 2003 and 2010 peaks. The amplitudes of the 1989 and 1997 pulses are not as great because their respective velocity fields were produced using image pairs spanning 4 years, so the peak velocity values are averaged with surrounding years, resulting in lower amplitudes. Based on the occurrence of the peaks as described here, the pulses of Ruth Glacier have a characteristic period of ~ 7 years.

Fig. 6. Temporal evolution of ice surface velocity on Ruth Glacier at 36 km and 43 km from 1973 to 2012. Five pulses are evident, with peaks in velocity in 1981, 1989, 1997, 2003 and 2010, resulting in a characteristic pulse frequency of ~ 7 years.
To further aid in analyzing the pulses, longitudinal profiles of velocity, acceleration and strain rate were produced for each velocity field (Figs 7–10). The longitudinal velocity and acceleration profiles in Figure 7a and b clearly show the extent of the pulse from 2009 to 2011. All the ice below the Great Gorge down to ~ 52 km noticeably accelerated during this time. It is worth noting that in the area of 27 km, 40–42 km and 49 km, there are inflections in velocity and acceleration, and prominent peaks (or troughs) in strain rate in 2009/10, 2010/11 and 2011/12. The location of these inflections, peaks and troughs approximately coincides with the transition from granitic to sedimentary bedrock at 28 km, a change from sedimentary to granitic bedrock at 41 km, and a change back to sedimentary bedrock at 48 km, as seen in Figure 1. Examination of the acceleration profiles (Fig. 7b) reveals the ice from 26 to 50 km accelerates (in varying amounts) simultaneously; there is no evidence of a wavefront propagating down-glacier. The strain rate between 37 and 43 km changes from predominantly compressive before the pulse, to tensile during the pulse, and back to compressive afterwards; again, indicating the ice in this area is responding simultaneously to applied stresses. The longitudinal profiles in Figure 8 span the years 1999–2006 and highlight the behavior of Ruth Glacier immediately before, during and after the 2002/03 pulse. As with the 2009/10 pulse, there are noticeable inflections in velocity and acceleration, and noticeable peaks or troughs in strain rate, near the transitions between granitic and sedimentary bedrock at 28, 41 and 48 km. Again, it is evident that the entire stretch of ice between 26 and 50 km has accelerated simultaneously, and the same pattern of changing strain rate, from compressive to tensile, and back to compressive, is evident before, during and after the pulse, respectively. The 2003/04 acceleration profile (Fig. 8b) shows a well-defined area of acceleration between 42 and 50 km, atop granitic bedrock; this same area also increased in acceleration in 2010/11 (Fig. 7b) while the rest of the ice up-glacier decelerated. Both of these acceleration events occurred 1 year after, and down-glacier of, the peak pulse events in 2003 and 2010, which occurred atop sedimentary bedrock. Figure 9 shows the longitudinal profiles for the years surrounding, and including, the 1987–91 and 1995–99 pulses. Although these two pulses are not as well defined as the 2002/03 and 2009/10 pulses, the same patterns are still evident. There are inflections in the velocity and acceleration profiles (Fig. 9a and b), and peaks or troughs in the strain rate (Fig. 9c), near the same locations as the later pulses, at 26 km, 40–42 km and 50 km. Again, large portions of the ice between 26 and 50 km accelerate and decelerate in unison. During the 1987–91 and 1995–99 pulses, there is no obvious acceleration of the ice between 42 and 50 km (Fig. 9b) (as seen in the later pulses (Figs 7b and 8b)), probably due to the poor temporal resolution of these two pulses. Figure 10 shows the longitudinal profiles for the years surrounding, and including, the 1980/81 pulse. Again, inflection points in the velocity and acceleration profiles are seen at, or near, 26, 40–42 and 50 km (Fig. 10a and b), but the pattern of peaks and troughs in strain rate seen in the other pulses is not clear. Lastly, it is noted there is a local velocity maximum at 26– 27 km in most of the longitudinal velocity profiles, where the glacier exits the Great Gorge. At this location the glacier spreads laterally, because its confining valley has increased in width from 2 km within the gorge to 3.5 km below, resulting in crevasses. It is speculated the crevasses act as a pathway for meltwater to enter the glacier and reach its base, thereby increasing basal slip or till deformation at this location, causing the local peak in velocity.
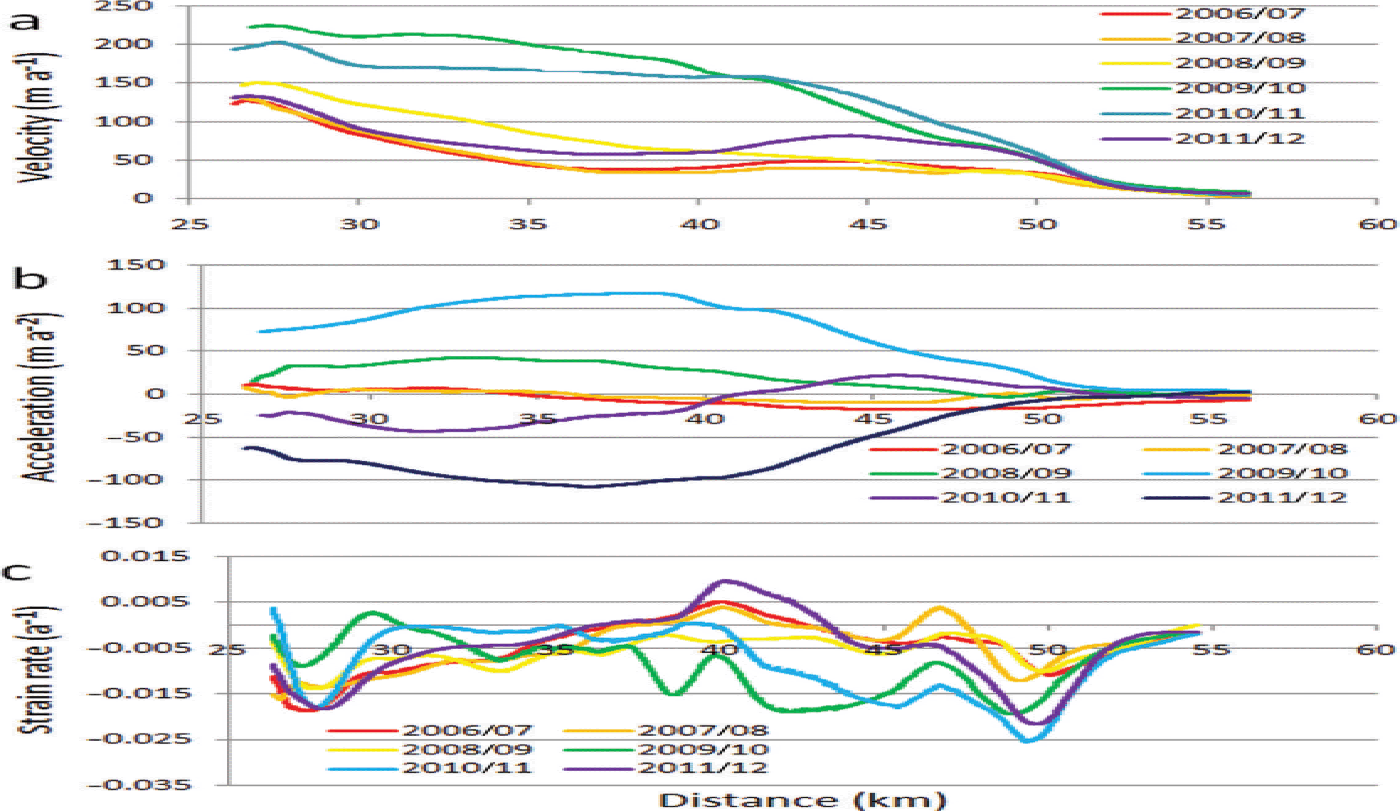
Fig. 7. Longitudinal profiles of ice velocity, acceleration and strain rate along the center-line transects shown in Figure 5, for the years 2006–12, which surround the 2009/10 pulse. (a) Ice velocity; (b) ice acceleration; and (c) longitudinal strain rate.
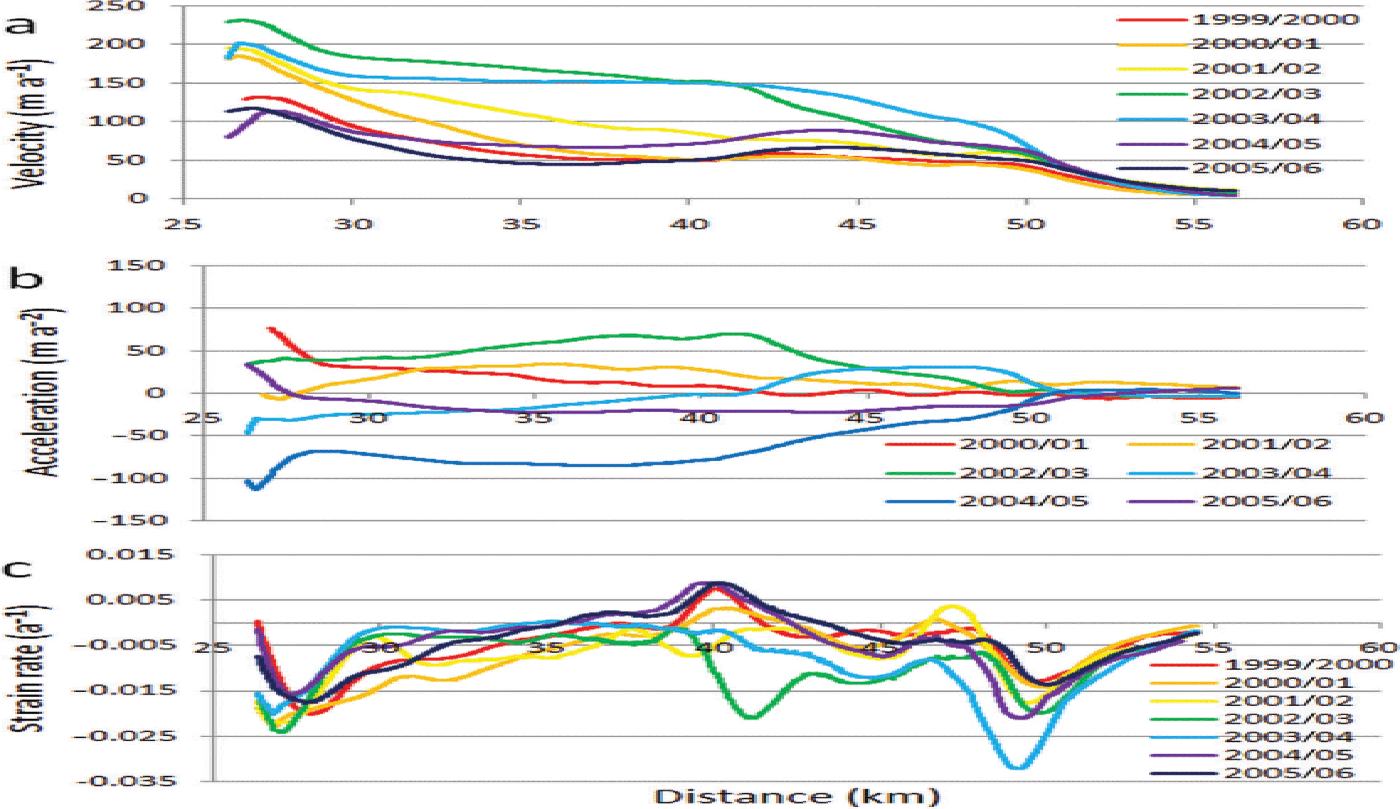
Fig. 8. Longitudinal profiles of ice velocity, acceleration and strain rate along the center-line transects shown in Figure 4, for the years 1999–2006, which surround the 2002/03 pulse. (a) Ice velocity; (b) ice acceleration; and (c) longitudinal strain rate.
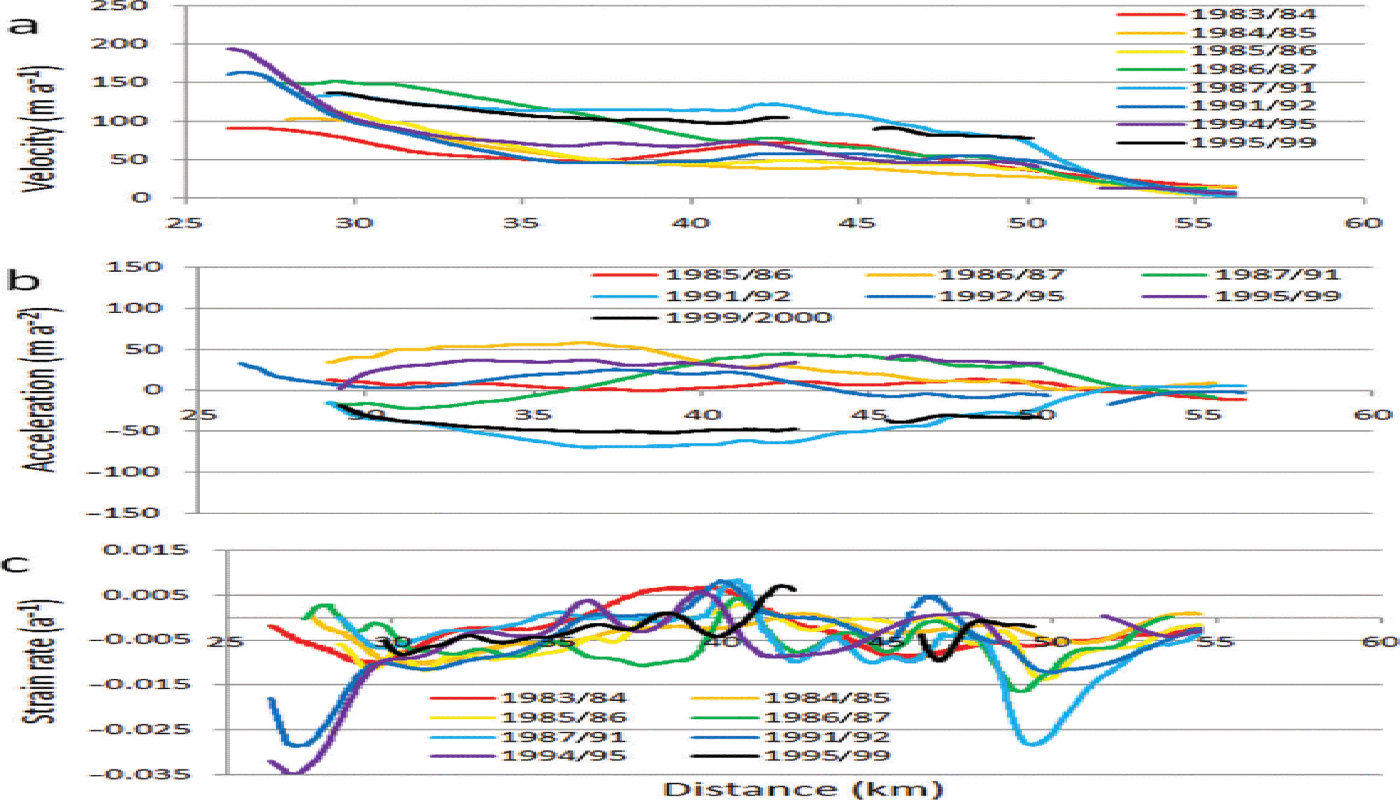
Fig. 9. Longitudinal profiles of ice velocity, acceleration and strain rate along the center-line transects shown in Figure 3, for the years 1983–99, which surround the 1987–91 and 1995–99 pulses. (a) Ice velocity; (b) ice acceleration; and (c) longitudinal strain rate.
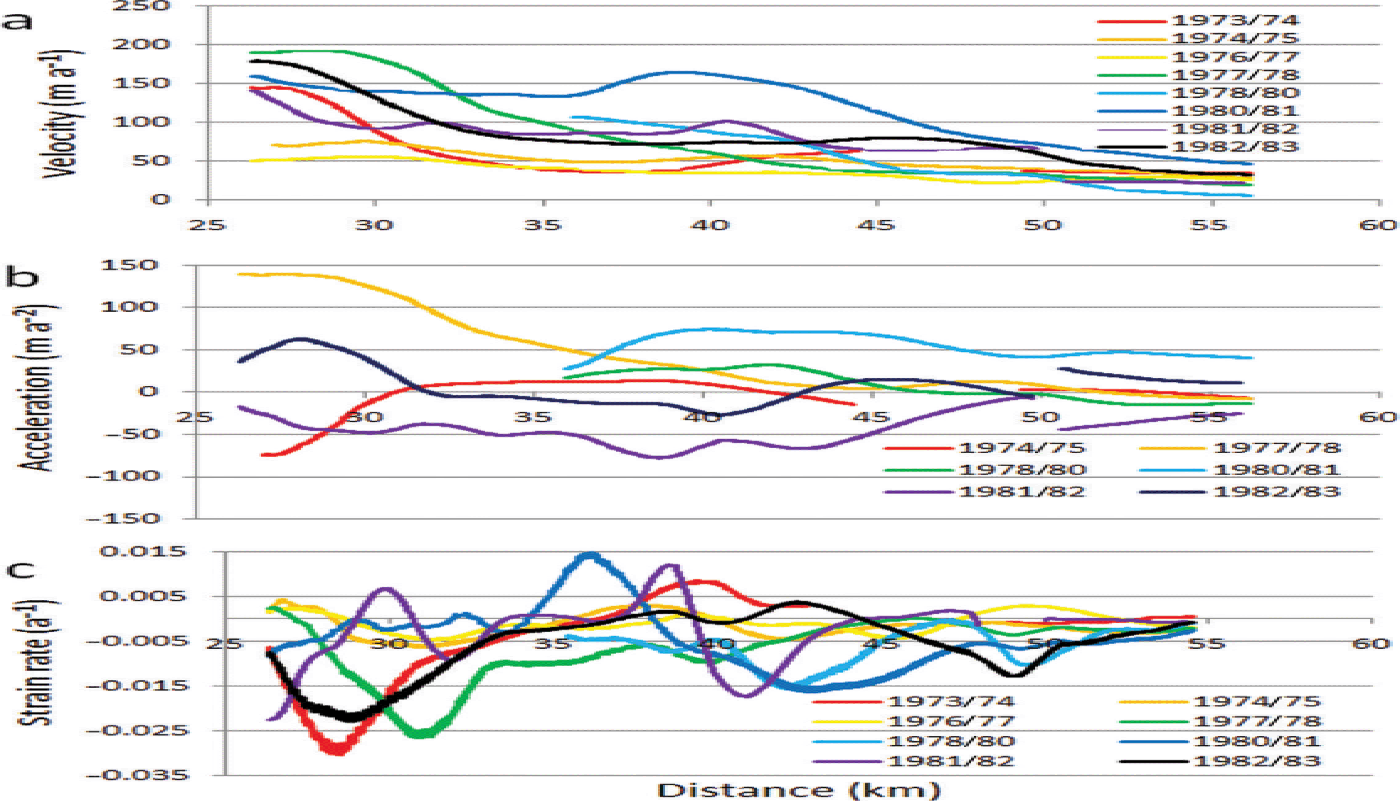
Fig. 10. Longitudinal profiles of ice velocity, acceleration and strain rate along the center-line transects shown in Figure 2, for the years 1973–83, which surround the 1980/81 pulse. (a) Ice velocity; (b) ice acceleration; and (c) longitudinal strain rate.
Discussion
To place our results in context with other surging and pulsing glaciers, we briefly discuss till deformation and flow instabilities with regard to glacier dynamics. In turn, these discussions help identify the likely basal conditions of Ruth Glacier during its pulses.
Glacier motion by till deformation
The location of surging glaciers in Svalbard is positively correlated with areas of fine-grained sedimentary bedrock, which are easily eroded (Reference Jiskoot, Murray and BoyleJiskoot and others, 2000), while in northwest North America surging glaciers are often found in fault-shattered valleys (Reference PostPost, 1969). Glaciers atop these areas are more likely to develop a soft bed than when atop intact crystalline metamorphic or igneous bedrock. Sedimentary bedrock will produce a fine-grained till that will have a low permeability which may be more prone to instabilities (Reference Murray and PorterMurray and Porter, 2001). Instability within a till may develop due to decreased effective pressure, via increased basal water input. As long as the discharge of water at the glacier bed is small, steady-state water pressure will approximate ice overburden pressure and the water will flow by Darcian transport through the till, or by a uniform water film at the base of the ice, and the till will remain consolidated. When pore-water pressure in the till equals or exceeds ice overburden pressure the till weakens and may dilate (Reference WillisWillis, 1995). Dilation of the till causes porosity and permeability to increase, thus decreasing water pressure and shear strength (Reference MurrayMurray, 1997). When a till dilates it can no longer support shear stress and it deforms, allowing the glacier to accelerate. The increased ice motion may occur as slip at the ice/till interface in which shear strain in the till occurs in the uppermost layer of sediment. Shear strain may also occur within the till along a plane of weakness, or it may be distributed throughout the till by the process of dilatant hardening. When a till dilates, pore volume increases, allowing water to flow towards the opening pores in the dilating sediment. If the rate of dilation is greater than the rate of pore-water flow then water pressure will decrease in the dilated sediment and it will harden (Reference ReynoldsReynolds, 1885). When the shear band hardens, the strain is focused elsewhere within the till; thus, the strain is distributed from one plane of weakness to the next.
Reference Truffer, Harrison and EchelmeyerTruffer and others (2000) suggest surges could be triggered by widespread dilation of basal till as shear stresses exceed a critical value, along with attainment of a glacier geometry that produces large basal shear stresses. Failed tills are concentrated under thicker ice, such as along the glacier center line, where driving stress is greatest and may exceed till yield strength. Reference NolanNolan (2003), when investigating the behavior of Black Rapids Glacier, proposed the idea of waves of till failure (activation waves) that propagate underneath a glacier as follows: (1) Failed till along a section of glacier center line causes increased stress laterally and longitudinally because the driving stress is redistributed elsewhere. (2) The glacier speed increases locally due to failed till. (3) When the driving stress is distributed elsewhere, any till that was at, or near, a point of failure will fail, thus increasing the area of the glacier with increased speed. (4) This process creates a wave of till failure and subsequent ice motion that propagates down-glacier via a positive feedback loop by continuously placing increased stress on the down-glacier till; (5) As the area of failed till increases longitudinally, the glacier moves faster everywhere because of reduced bed friction and greater basal motion. A similar mechanism was discussed by Reference Frappé and ClarkeFrappé and Clarke (2007) to explain the surge of Trapridge Glacier. The till deformation paradigm allows glacier velocity to increase greatly without requiring large changes in glacier geometry or the subglacial hydraulic system, assuming the till is near its failure threshold (Reference Truffer, Echelmeyer and HarrisonTruffer and others, 2001).
Reference Fowler, Murray and NgFowler and others (2001) noted that if the till layer has a low transmissivity (i.e. the till is thin) and low permeability, then oscillations in effective pressure, ice thickness and ice flux can occur. Ice speed during a pulse depends primarily on basal roughness. If the basal roughness is large, then ice flow is sufficiently restricted to allow oscillatory behavior to occur; otherwise, a major surge can occur if the basal roughness is small, because there is little restriction to ice flow. Reference Fowler, Murray and NgFowler and others (2001) also suggest that if a glacier is temperate and resides atop a thin till, the ice may activate (i.e. the till fails beneath it) before any significant ice motion because the activation waves are faster than the ice motion; so the ice slumps forward rapidly moving as a block, or plug. Therefore, there is no surge front that would otherwise separate fast-moving surging ice and slow-moving quiescent ice. Plug flow has been observed on Black Rapids Glacier (Reference Harrison and PostHarrison and Post, 2003) and Trapridge Glacier (Reference Frappé and ClarkeFrappé and Clarke, 2007), both of which have surged atop a till. Once a surge has been initiated by till failure, less stress is required to keep the till in a failed state, allowing the surge to continue. This occurs because drag at the glacier base increases longitudinal shear stress that might cause a till to fail even when water pressures are less than the critical Coulomb threshold (Reference Boulton, Dobbie and ZatsepinBoulton and others, 2001). The accelerated ice motion will cease when the ice can no longer be shoved forward by driving stresses, either by obstacles restricting down-glacier movement or by decreased up-glacier stresses, then the basal shear stress decreases below the till failure point and the till heals. Alternatively, the accelerated ice motion will cease if drainage of water from the till occurs, reducing water pressure and allowing the till to heal. However, a till with low permeability may not drain completely; thus, the till may not fully heal and it is left primed for another pulse episode when enough water is introduced again (Reference NolanNolan, 2003). A thin till, which has less water storage capacity than a thick till, will refill quickly and surpass its Coulomb failure threshold sooner than a thick till would, resulting in more frequent pulses.
Basal conditions beneath Ruth Glacier
Knowing that the sedimentary bedrock beneath Ruth Glacier is highly fractured and easily eroded, and the fact that Ruth Glacier exhibits a dynamic behavior similar to other glaciers known to reside atop deformable tills by accelerating and decelerating in a cyclical, plug-like fashion, it seems likely a deformable till exists beneath Ruth Glacier between 28 and 41 km. The area from 41 to 48 km is underlain by granitic bedrock that will not as readily erode to produce a till, but there is likely some sediment beneath the glacier in this area that was transported from above, but which is spatially sparse and does not promote widespread increased ice motion via till dilation and deformation. The fact that the ice in this area (lying atop the granitic bedrock) has accelerated during the pulses, although to a lesser degree than ice atop sedimentary bedrock, is likely due to stress transfer and longitudinal coupling with the ice up-glacier (note the lesser velocity at 43 km in Fig. 6 compared to 36 km). The inferred existence of a deformable till requires the basal ice and the till to be at the pressure-melting point; therefore, we conclude Ruth Glacier is warm-based. The simultaneous acceleration of the ice from 26 km, immediately below the Great Gorge, to ~ 50 km, and the lack of a wavefront, provide further evidence that Ruth Glacier is warm-based, because Reference Fowler, Murray and NgFowler and others (2001) propose that temperate glaciers atop deforming tills will slump forward, thus no wavefront forms. The lack of a wavefront is in contrast to observations of typical Alaska-style surging glaciers wherein a surge front separates quiescent ice from surging ice, as noted on Variegated Glacier (Reference KambKamb and others, 1985) and Bering Glacier (Reference Roush, Lingle, Guritz, Fatland and VoroninaRoush and others, 2003; Reference Turrin, Forster, Larsen and SauberTurrin and others, 2013). The dynamic oscillating (pulsing) behavior of Ruth Glacier suggests the till is thin with a low permeability (Reference Fowler, Murray and NgFowler and others, 2001).
Distinguishing pulses from surges
Alaska-style surges are controlled by the morphological evolution of the basal drainage system beneath temperate ice from a channelized system to a distributed cavity system (Reference KambKamb and others, 1985) and are traditionally assumed to occur atop a hard bed. Svalbard-style surges are controlled by the thermal evolution of the basal ice from sub-freezing to temperate (Reference Fowler, Murray and NgFowler and others, 2001; Reference Murray, Strozzi, Luckman, Jiskoot and ChristakosMurray and others, 2003) and occur atop a soft bed (a basal till). Both Alaska-style and Svalbard-style surges can result in a surge front (kinematic wave) moving down-glacier that separates quiescent ice, moving primarily by internal deformation of the ice column, from surging ice that moves primarily by slip at the ice/bed interface, or by deformation within a basal till (in the case of a Svalbard-style surge). If the till beneath Ruth Glacier froze between pulses, then a surge front would form in the manner of a typical Svalbard-style surge during each pulse, but the lack of any wavefront suggests the base is perennially warm, and Ruth Glacier is not known to surge in the traditional sense. As noted above, Trapridge Glacier experienced five low-amplitude pulses during a prolonged surge (Reference Frappé and ClarkeFrappé and Clarke, 2007), and Black Rapids Glacier, also a surge-type glacier, experienced two low-amplitude pulses during quiescence (Reference NolanNolan, 2003). These two studies, and the current observations of Ruth Glacier, tentatively suggest pulsing is a dynamic behavior apart from typical surging, because pulses have been observed during a surge, during quiescence and on a non-surging glacier. However, the underlying controlling mechanism is unidentified.
Implications for decadal-scale velocity measurements
Optical feature-tracking methods have now matured to the point where decadal-scale regional, and perhaps global, studies of ice dynamics are possible, as exemplified by Reference Heid and KääbHeid and Ka¨a¨b (2012a). When performing regional or global studies with the goal of identifying long-term regional trends in ice dynamics, conclusions made from decadal-scale velocity measurements, such as whether the glacier has accelerated or decelerated over time, must therefore account for the short-term cycles that may have been overlooked. Similarly, conclusions made regarding mass balance based on decadal-scale velocity measurements must also be based on large regional studies incorporating numerous glaciers. This way the dynamic behavior of a few glaciers with short-term cycles is averaged out, or may be readily identified as anomalies, and will not negatively affect the results. Thus, regional influences such as climate become apparent, rather than local short-term effects, such as pulses. As an example, Reference Heid and KääbHeid and Kääb (2012a) noted Ruth Glacier accelerated between 1986/87 and 2009/10. This perceived acceleration is a result of the years chosen for use in their velocity determinations. The 1986/87 period falls between pulses, while the 2009/10 period is at the peak of a pulse (Fig. 3), so there is a perceived acceleration of >120 m a–1 during this period. If one had instead chosen images acquired in 1980/81 and 2007/08 and performed the same analysis, the result would be a deceleration of >120 m a–1, the opposite of what Reference Heid and KääbHeid and Kääb (2012a) reported. In either case, the pulses that occurred during the interval between velocity measurements are missed. However, the overall conclusion of Reference Heid and KääbHeid and Kääb (2012a), that land-terminating glaciers have decelerated over the past several decades, is valid due to the large number of glaciers in the study from several widespread regions.
Conclusions
From 1973 to 2012, a span of 39 years, Ruth Glacier experienced five pulses that have gone unnoticed until now. These pulses are of low amplitude compared to typical surges of glaciers in Alaska, and they occur without causing an advance of the terminus and without widespread crevassing, perhaps helping to explain their oversight. The pulses have occurred on a regular basis, approximately every 7 years, with peaks in 1981, 1989, 1997, 2003 and 2010, and with increases in ice velocity of >120 m a–1 during the peaks in 1981, 2003 and 2010. We suggest that the pulses are a result of enhanced basal motion due to deformation of a subglacial till. Therefore, we infer that the base of Ruth Glacier, in the area in which the pulses occur, must be temperate. Additionally, analytical modeling predicts that the manner in which the glacier moved during the pulses, with a 20 km section of ice accelerating and decelerating in unison, and the lack of a wavefront, is suggestive of a perennial temperate base (Reference Fowler, Murray and NgFowler and others, 2001). The oscillating dynamic behavior is interpreted to be due to a thin till with low permeability that is just above a critical value (Reference Fowler, Murray and NgFowler and others, 2001). The basal roughness is speculated to be great enough to restrict ice flow and prevent the occurrence of major surges. These findings illustrate the influence of bedrock lithology and a glacier’s basal thermal regime on its dynamics, the combination of which will ultimately affect its mass balance.
Acknowledgements
This project was funded by NASA grants NNX08APZ76 and NNX08AX88G. We thank Peter Haeussler of the US Geological Survey for providing information on the geology of the Mount McKinley area. We also thank the reviewers, including Garry Clarke and John Woodward, for helpful comments.














