1. Introduction
Visual stratigraphy (VS) is the most basic data one can obtain from an ice core (Reference AlleyAlley and others, 1997). It can be acquired using many techniques ranging from simple ocular inspection and notes to digital scanning at high resolution. VS can be acquired in the field, in a cold laboratory or directly in a borehole, using a variety of different light sources from the sun via light tables to complicated light set-ups (Reference BensonBenson, 1960; Reference PohjolaPohjola, 1994; Reference Kameda, Narita, Shoji, Nishio, Fujii and WatanabeKameda and others, 1995; Reference AlleyAlley and others, 1997; Reference Hawley, Waddington, Alley and TaylorHawley and others, 2003; Gow and others, 2004; Reference Takata, Iizuka, Hondoh, Fujita, Fujii and ShojiTakata and others, 2004; Reference SvenssonSvensson and others, 2005). VS builds on the observation that ‘Stratifications in firn, as other sediments, reflect differences in the environment of deposition and diagenesis’ (Reference BensonBenson, 1960), i.e. the visual appearance of snow and ice is affected by the surroundings: summer snow is often coarser than winter snow, occasional melt results in ice layers, and the influence of different impurities affects the colour and structure of ice and snow. Further, VS has a strong correlation with other records, such as chemical impurities and dust (Reference SvenssonSvensson and others, 2005), and can also be used for dating ice cores (Reference AlleyAlley and others, 1997; Gow and others, 2004; Reference Takata, Iizuka, Hondoh, Fujita, Fujii and ShojiTakata and others, 2004; Reference SvenssonSvensson and others, 2005). The development of digital recording and processing utilities (e.g. digital scanners, cameras, computers and storage media) has made analysis of VS more manageable than in the past (Reference AlleyAlley and others, 1997).
The relationship between drill depth and water equivalent depth is important for any interpretation of ice-core data. If the density is highly variable, as in ice cores taken from the percolation zone (i.e. the firn contains frequent ice lenses), the density record is even more crucial for drill depth to water equivalent conversion. Hitherto, the density record from ice cores has been achieved by weighing bulk samples of the ice (Gow and others, 2004), ocular inspection of ice facies (Reference PohjolaPohjola and others, 2002), dielectric profiling (DEP) analysis (Reference Wilhelms, Kipfstuhl, Miller, Heinloth and FirestoneWilhelms and others, 1998), and through analysis of gamma-ray scattering (Reference Gerland, Oerter, Kipfstuhl, Wilhelms, Miller and MinersGerland and others, 1999; Reference WilhelmsWilhelms, 2000 cited by Reference Eisen, Nixdorf, Wilhelms and MillerEisen and others, 2002) and neutrons (Reference Morris and CooperMorris and Cooper, 2003). In this paper, we use digital photographs to obtain a high-resolution density proxy record from an ice core through a simple photographic equipment set-up and minimal laboratory work.
2. Field Site and Core Material
In April 2005, a 125 m long ice core was drilled at a saddle point on Holtedahlfonna (79.1374°N,13.2723°E; 1150 m a.s.l.), about 40 km northeast of Ny-Ålesund on the west coast of Spitsbergen, Svalbard (Fig. 1). An earlier expedition in August 1992 drilled a core in the same area (within 500 m), where the 1963–92 mean accumulation rate was found to be 0.48 mw .e. a–1 based on tritium concentrations (Reference Goto-AzumaGoto-Azuma and others, 1995). Tritium analysis on our core compares well to this finding. Ice temperature data from a thermistor string suggest that the drill site is situated very close to the wet snow line, i.e. the line dividing the percolation and wet snow zone (Reference PatersonPaterson, 1994). Radar measurements show that the ice depth in the area is highly variable and that it is approximately 150 m at the drill site. However, due to water-saturated ice layers close to the core, the depth from radar surveys is uncertain, and temperature modelling suggests a depth closer to 200m. The drill used was custom-made by the University of Utrecht and British Antarctic Survey and had a core diameter of 105 mm. The core was retrieved in sections of approximately 60cm, giving a total of 210 pieces. No drilling fluid was used. More details on the drill can be found online (Reference Mulvaney, Bremner, Tait and and AudleyMulvaney and others, 2002).

Fig. 1. Map of the Svalbard archipelago and the drill site at Holtedahlfonna.
3. Method
3.1. Photographic set-up
During the sampling of the ice core for stable-isotope and chemical analysis, 3 cm thick longitudinal (vertical in the glacier) slabs were cut from the middle of each piece of ice core. The slabs were brushed to remove loose particles and put on a black table (Fig. 2). The slabs were illuminated from one side (45–90° compared to vertical) using fluorescent lights behind a translucent plastic screen. At a height of 20 cm above the ice, a compact digital camera was mounted, facing downwards, on a sliding rail with distinct stops every 10 cm. The digital camera was a 5 megapixel (red, green, blue) 3 × 8 bit RGB (red, green, blue) charge coupled device (8 bits means that the pixels can take values between 0 and 255). A yellow ruler was placed along the ice for reference. Overlapping photographs with a resolution of approximately 100 pixels cm–1 were taken along each slab (except for cores 1 and 2), producing over 1200 images. No under- or overexposure was detected.

Fig. 2. Photographic set-up showing the ice slab from the short side. The camera is mounted on a sliding rail (moving in and out of the figure). The width of the slab is 10 cm and the distance between the ice and the focal plane of the camera is 20 cm.
3.2. Image treatment
The image processing was completed within MATLAB® (with the image-processing toolbox), although other software (e.g. freeware like Octave or Scilab) can be used. The original images from the camera had a slight barrel distortion, which was removed using MATLAB® (www.mathworks.com/ products/demos/image/create_gallery/tform.html). (Barrel distortion causes the central part of an image to have greater magnification than the lateral parts. This makes straight lines close to the edge look bent;a rectangle will look swollen, like a barrel. Pillow distortion gives the opposite result.) These lens errors are common in consumer-level zoom lenses and can be removed in most photo-editing programs (e.g. Adobe Photoshop® or Gimp®). In order to reduce the number of data, the images were cropped and re-sampled with a Lanczos filter using IrfanView batch conversion (IrfanView is a freeware program for digital image processing: http://www.irfanview.com). Next, the images were attached core-wise by taking the central 10cm of each image (in MATLAB®), producing a total of 208 core piece images.
For analysis, the non-ice parts of the images had to be removed (i.e. by setting pixel intensity to 0). To remove the background in the top part of the image, a 16 × 4 pixel edge detection filter (two rows of –1 and two rows of 1) was applied from the top (Reference Gonzalez and WoodsGonzalez and Woods, 2002; MATLAB® function imfilter). The same approach was used from the left and right. The yellow ruler was removed easily by finding and closing morphologically (Reference Gonzalez and WoodsGonzalez and Woods, 2002; MATLAB® function imclose) the yellow part of the image. The resulting images have a resolution of approximately 17 pixels cm–1, which is sufficient for this analysis.
4. Results
4.1. Image intensity as a function of density
There are many variables determining the reflection and scattering of light in snow and ice, one of which is density (Reference BensonBenson, 1960; Reference Wiscombe and WarrenWiscombe and Warren, 1980; Reference Hawley, Waddington, Alley and TaylorHawley and others, 2003; Reference Wilen, DiPrinzio, Alley and AzumaWilen and others, 2003). However, many of these variables are related to each other. The amount of light both reflected and scattered by ice and snow depends, to a high degree, on the amount of air and air–ice interfaces. Since density is also a function of air content in the ice, there is a relationship between image intensity and core density. With side illumination, snow and firn is brightest in the images, and bubbly ice darkens with decreasing number of bubbles. If the ice is illuminated from below (Reference BensonBenson, 1960, p. 19;Reference KaczmarskaKaczmarska and others, 2006), the relationship is reversed, since light is transmitted or blocked by snow rather than being passed through or scattered and reflected. When the firn is transformed to ice, ice from more porous firn (e.g. hoar) contains more air bubbles (Reference SchwanderSchwander and others, 1993) and hence is lighter/brighter so that the signal is preserved. The intensity–density relationship is simplified since many other variables such as crystal orientation, crystal size and impurities influence the optical properties of the ice. However, as we will show, this generalization is good enough for the application at hand.
Figure 3a is a composite of five images and shows the slab from the core piece taken between 27.84 and 28.40m drill depth. The core piece contains both bubbly ice and firn. The drop in intensity with increasing row number (the direction of the arrow in Fig. 3a) is caused by the distance from the light source (Fig. 2). Note that the firn image is brighter than the denser bubbly ice, which creates a difference in the intensity between Figure 3b and c.

Fig. 3. (a) A composite of five images. Up and Down point toward the glacier surface and bed, respectively. (b, c) Row-wise average intensities of two types of ice: bubbly ice (b) and firn (c). The arrows point away from the light source. The dashed lines are logarithmic fits.
A representative light intensity value for each depth is determined by using the mean intensity value of the image column from about 80% of the ice core width (equal to cutting approximately 25 pixels at the start and end in Fig. 3b and c). This removes the edge effects, and evens out small features like large bubbles and small cracks. On the other hand, using such a wide part of the image smooths out oblique objects and may make thin oblique ice lenses disappear completely.
The complexity of the photographic set-up makes it difficult to apply an exact physical theory to derive ice density from the images. The light recorded by the camera is a mixture of light entering the ice from the side (transmittance and subsequent scattering through the ice) and light reflected on the surface. Also, the reflection angle is widespread and varies over the slab. For this reason, an empirical approach was chosen to link density to light intensity.
The transfer function between image intensity and ice density was determined by deriving a regression equation between the bulk mean intensities and the bulk densities obtained by weighing each piece of ice core (Fig. 4). The bulk densities are not very reliable since the volume is determined from the bulk length and an average diameter, and uneven ends of the core pieces will decrease the accuracy considerably. Figure 4 shows an exponential relationship between bulk density and bulk intensity. Since the density data have a considerable variance, there are nearly an infinite number of regressions for a transfer function, which all will give roughly the same fit. We chose one of the simplest:
where ρ is the density (Mgm–3), INT is the image intensity (0–255) and the constants are a = –1.95 × 10–9, b = 44.4 and c = 0.92. The density derived from image intensity is called INT density.

Fig. 4. Regression curve between the 208 bulk densities from the core weight and the bulk mean intensities from the image analysis.
4.2. DEP density data
Density was also derived from a guarded capacitor dielectric profiler (DEP;Reference Wilhelms, Kipfstuhl, Miller, Heinloth and FirestoneWilhelms and others, 1998), which measures conductance and capacitance at 250 MHz at 5 mm depth increments. We use the capacitance of the ice, Cp, and of the empty cradle, Cair, to derive an estimate of the relative permittivity, εr:
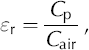
where C air = 65.7 × 10–15 F for this set-up. The density can be calculated from the permittivity through an empirical equation as:
(Reference Kovacs, Gow and MoreyKovacs and others, 1995). This method does not use bulk densities for calibration. However, a number of adjustments are required before the data are ready to use. Although the DEP has the potential to sample at high sampling rate, the actual resolution is lower due to the wide footprint of the electrode, which smooths the result. The capacitance and conductance are influenced by an additional 25 mm of ice around the measurement point. Therefore, the first 25 mm at the beginning and end of each core piece are affected by the air outside the core (which significantly decreases capacitance and conductance since the capacitance and conductance of air is much lower than that of ice). The core is thus filtered for all edge and cracking effects that are caused by air intrusions. Also, since the capacitance and conductance are affected by the ice chemistry, we use the conductance peaks to remove sections where chemistry, rather than differences in density, is driving the capacitance.
4.3. High-resolution correlation
Both the DEP and the INT densities are capable of delivering high-resolution density (5.0 and 0.5 mm). By down-sampling the INT density we can compare both density series at 5 mm resolution. An initial analysis shows that the two datasets correlate well (r = 0.91;see also Fig. 5). However, a large part of the correlation reflects the fact that the density increases with depth. A further complication in evaluating the significance of the correlation is the skewed distribution of ice vs firn data points (Fig. 4).

Fig. 5. The DEP, INT and weighed (Bulk) density records plotted vs depth, together with the expected density ρ(z) For better visibility, the data have been smoothed using a Gaussian filter with σ = 0.5 m. The thin dashed black curve is the calculated density ρ(z) using Equation (5).
A fairer comparison of the high-resolution capabilities of these two measurements was made by removing the depth dependency, leaving only the small-scale variations residual (ρ res = ρ–ρ(z)). To do this, a function of density depending on depth only, ρ(z), is required. Using the assumption that firn is compacted as a function of load (Reference BensonBenson, 1960) did not fit our data. Instead, we assume the density change with depth is proportional to the deviation from the density of pure glacier ice (Reference Herron and LangwayHerron and Langway, 1980, referring to Reference SchyttSchytt, 1958):
where K is a constant. Solving the equation (by separation and integration) using ρ(z = 0) = ρ snow yields a calculated density,
The best fit to our data is achieved by using K = –0.1, ρ ice = 0.908 and ρ snow = 0.350. The latter two also fit well to standard values for wind-packed snow and glacier ice (Reference PatersonPaterson, 1994). According to those values, the transition depth (i.e. pore close-off, where ρ = 0.83 Mg m–3; Reference PatersonPaterson, 1994) is situated at about 19.7m (Fig. 5). Although very simple, this function serves the purpose of removing the density dependence on depth, leaving only local variations. All three density records plus the calculated ice density from Equation (5) can be seen in Figure 5.
The resulting correlation between the INT and DEP density residuals (ρ resINT = (ρINT–ρ(z)) and ρresDEP = (ρDEP–ρ(z))) using the whole core is still high, r res = 0.69, but, as can be seen in Figure 5, density varies more in the shallower part of the record than in the deeper part. This means that the firn part dominates the correlation between ρ resINT and ρ resDEP; the good fit in the firn part masks the poorer fit of the ice part. To be able to see how much the correlation varies with depth, we derive the correlation for 5 m parts, i.e. the correlation for each 5 m section beginning at the top (Fig. 6).

Fig. 6. The correlation coefficient between the residuals ρ resINT and ρ resDEP at 5 mm resolution using 5m intervals.
Figure 6 shows that the correlation is high in the upper parts of the core, but decreases with depth and is low below 55 m. Eliminating possible mismatches between the two records by re-sampling to lower resolution (5 cm, i.e. taking 5 cm averages) gives approximately the same result as the high-resolution (5 mm) example. This decrease in correlation with depth is likely due to noise, or the fact that the variations in the deeper part are smaller (see Fig. 5), i.e. INT/ DEP variations that are not a result of density differences become more important. The significance level is difficult to determine since the data have a high degree of autocorrelation (i.e. if sample yi is heavy, the chances of yj+1 being heavy is larger than if yi had been light).
4.4. Core-wise correlation
By taking the core-wise mean density from INT density and DEP density, it is possible to compare them to the weighed bulk densities for each core part. Again, calculating the correlation on the whole record only reflects the fact that density increases with depth. We therefore used the same residual approach as in section 4.3. We also calculated the root mean square (rms) of the differences between the density records. Since r was found to differ between the top and bottom part of the core, a separate analysis of the record above and below, 40 m depth (66 and 142 bulk samples, respectively) was completed. The results are shown in Table 1 where the three different density records are only comparable in the upper/less dense part of the core. From the data at hand, it is not possible to say which one is the most correct, but it is clear that ρINT and ρDEP are more comparable to each other than to ρ Bulk.
Table 1. Table 1. The correlation and difference between the bulk samples. ‘All’ is using the whole core (208 samples), ‘Top’ is above 40 m (66 samples) and ‘Bottom’ is below 40 m (142 samples). rms is the root mean square of the difference between the records. r is the Pearson correlation coefficient

4.5. Water equivalent scales
One of the main reasons to determine ice-core densities is to retrieve a water equivalent depth scale. This can be done by weighing and measuring the bulk pieces, but with DEP or image analysis the resolution is enhanced. To assess how much the accuracy is improved, the difference between the water equivalent scales from the low-resolution bulk density and the two high-resolution records (i.e. cumulative sums of ρBulk–ρDEP and ρBulk–ρINT) is plotted (Fig. 7). The difference is never larger than 0.45 mw.e. and this is at 60 m depth. This means that if a dating horizon is found at 60 m drill depth (~-49 m w.e. or about 100 years), the average accumulation rate derived from this horizon, depending on which density method is used, will differ by about 1%. The reason for the difference between DEP and INT density is unclear and cannot be determined from the data.

Fig. 7. The difference in m.w.e. between the two density proxies (ρDEP and ρINT) and ρBulk.
5. Discussion
5.1. Comparison between ρDEP and ρINT records
The major benefits of the image intensity density method is that it is inexpensive, fast and simple compared with other high-resolution methods like DEP and line scanning. Although some office time is required to evaluate the images, very little extra time in the cold laboratory is needed to take the photographs, especially when the core needs to be sampled anyway (<1 min extra per core piece). Cold-laboratory processing time is minimized compared with earlier visual stratigraphy as the cores are simply brushed instead of microtomed (Reference AlleyAlley and others, 1997). The INT method has a better resolution than the DEP approach. The footprint of the DEP is wider than the 5 mm increments used here, while the INT method has a resolution of millimetres, which makes it more suitable for detection of small ice lenses and sharp transitions. The INT method also inherently provides a photographic record of the core, which serves as a raw data archive that can be re-evaluated if questions about the derived data arise. The drawback of the INT method is that differences in intensity are not necessarily mean differences in density, since other variables are involved (i.e. grain size, orientation, etc.; Reference Hawley, Waddington, Alley and TaylorHawley and others, 2003). In addition, the relationship between intensity and density is not physically based;the bulk densities are required to establish a transfer function.
The DEP method has the advantage of being physically based; no bulk samples are needed to derive a transfer function. The DEP method is non-destructive, no sawing is necessary and a conductivity record is retrieved at the same time, which can be used to determine major volcanic events as well as being a valuable dating tool (e.g. Karlöf and others, 2000). A drawback of the DEP method is that chemistry alters the capacitance record (Reference Wolff, Miners, Moore and ParenWolff and others, 1997). Also, the actual footprint of DEP is much wider than the data resolution of 5 mm, and thus INT resolution is higher. Furthermore, ice sedimentary structures are more noticeable through the image analysis than by DEP. Figure 8 shows an example in which the image intensity data differentiate between bubbly and clear ice, while the DEP data do not. In most samples, DEP and INT are quite comparable. The only difference is that the DEP record is smoother. Also, more data are lost from each core through DEP due to the edge effects of the wider footprint. Thus, sharp density transitions and thin layers are lost, which is a problem if the density is going to be used to determine a climatic signal (Reference KaczmarskaKaczmarska and others, 2006) or to simulate a radar output.

Fig. 8. The image intensity, capacitance, conductance and image from bulk sample number 125, 73.55–74.15 m drill depth. The conductance is dashed. Note that the image intensity has a peak at the crack (73.91m depth).
So which method is the best for general purposes? By inspection, it seems that the INT method does a better job differentiating between structural properties like clear ice, ice with large bubbles and ice with many small bubbles (Fig. 7). This might be due to the fact that DEP is more sensitive to chemical variations. Since we have no accurate measurements of the small-scale densities of the ice, we cannot say which is the best proxy for density. Both methods perform well in the upper part of the core, where the density is highly variable. The increased density accuracy is not necessary for determining accumulation rates, but the ice intensity record is useful for detecting climatic signals using a stratigraphic melt index (i.e. the ratio between bubbly and less bubbly ice) (Reference KoernerKoerner, 1997). In conclusion, the INT method is best in stratigraphic analysis, both for creating a climate signal and for evaluating how other records might have been affected by processes in the snow and firn, for example diffusion of δ 18O. Also, the INT method is more reliable in cases where small features and sharp transitions are crucial (i.e. when simulating radar reflections in an Arctic ice core with several melt features). Lastly, image analysis is also helpful for interpreting what the DEP is actually measuring (Reference Brandt, Kohler and LangleyBrandt and others, 2005) and may possibly be used for increasing the resolution of DEP data.
5.2. Benefits and drawbacks of the photographic set-up and suggested improvements
There are two advantages of illuminating the core from the side instead of from below (Fig. 2). The first is that the result is easy to interpret by simple ocular inspection since the images are similar to our visualization of snow and ice (the more snow-like the core, the lighter the image). The second is that variations due to slab thickness are decreased.
By increasing the distance between the camera and the ice, the height distortion, i.e. geometric distortion (Reference Lillesand and KieferLillesand and Kiefer, 1994, p. 135) due to the bottom of the slab being further away from the camera than the top, can be mini-mized. This requires a lens with greater focal length, which further increases the need for a stable camera mount to avoid blurred photographs. A simple digital single-lens reflex camera with a fix focus lens about 50 mm increases the image quality significantly, both with respect to height and barrel/pillow distortion.
By using a better background, the image treatment can be simplified. First, no white elements must be present close to the slab. In our set-up, the device used to place the slab in the right position was an unsuitable colour. Easily (digitally) recognizable markers, for example strong colour dots (magenta, pure red, yellow, etc., which normally will not be found in the ice core), should be used on the photographic bench to simplify the image analysis involving rectifying, scaling and merging the images. This also decreases the requirements of the photographic bench and makes the work in the laboratory much less critical: a slight mistake in the position of the camera is easily corrected by the computer
Through a better light set-up, it is possible to use a physical approach to relate the light intensity and density. We had only a few hours to evaluate the set-up used here before the core cutting began, and many improvements could be made through experimenting (Reference AlleyAlley and others, 1997). The light source should be further away from the ice to avoid the intensity fall-off caused by the changing angle of the reflected light (Fig. 3b and c). It is also beneficial to try different angles and to use light from above only. The ends should be photographed strictly from above to avoid capturing the light entering and exiting the short end of the ice slabs (i.e. if the core is 558 mm long, when taking the end image, the slider should be on 558 mm instead of the distinct stop at 500 or 600 mm). This will mean that the last image should be taken at different positions for every core (because the core length varies), but by using background markers the position of the camera is easily detected.
Marks on the core caused by the saw teeth or ice dust on the slab might affect the data slightly, and care must be taken to minimize this. Microtoming takes too much time, but alcohol wiping (Reference AlleyAlley and others, 1997) will probably improve the result without increasing the time needed. In a later set-up, dust and saw marks were eliminated by melting the surfaces of the core slab using a ski waxing iron. However, this technique might affect the chemistry of samples taken from the slab.
6. Summary
We have shown that digital images can be used as a simple and fast method to obtain a high-resolution density record for the upper part of an ice core containing several melt features. Compared with the DEP method, the image intensity method is less expensive, faster and has a simpler set-up. It is less sensitive to cracks and crushed ice (Reference AlleyAlley and others, 1997), hence is able to retrieve data closer to cracks and core ends. The resolution is higher (since the wide footprint of DEP smooths the data), and bubbly layers and other visible features are better represented than with DEP. In search of indications of melt/no melt, image analysis is superior to DEP. On the negative side we note that the image analysis density needs another record (the bulk density) for calibration, while the DEP can be calibrated using standardized plastic tubes. We also suggest a better photographic setup, which will both improve the data quality and speed up post-processing time.
Acknowledgements
We thank E.-J. de Jong for his great work running the ice-core drill, C. van der Veen for help with the drilling, and G. Floor and K. Virkkunen for help with cutting the core in the cold laboratory. Thanks to Norsk Polarinstitutt, Swedish Science Council, Ymer-80 and Sernanders stipendium for financial and logistic support. Additional funding for the drilling project was obtained from the Netherlands Organization for Scientific Research (NWO). We also acknowledge the scientific editor T. Scambos and the helpful comments of the reviewers Z. Courville and C. Shuman.











