Introduction
The development and motion of snow avalanches is governed by three independent contributions: the amount of snow, the morphology of the avalanche path (slope, curvature) and the rheological properties of the snow. Snow avalanches may display highly complex features. Longitudinally, the avalanche is made of a front followed by a core and a tail. The flow also presents a strong vertical stratification of velocity and sometimes of density. In this latter case, less frequent in the Alps, the lower layer of the flow consists of a dense granular suspension highly sheared at its base. The upper layer consists of a highly dilute suspension. An intermediate fluidized saltation layer connects these two layers and ensures mass and momentum exchange. Each layer of the avalanche is characterized by an appropriate dynamic regime, ranging from dense granular to turbulent dilute suspensions. Highly complex mechanisms are involved in these various flow regimes, in erosion and deposition, as well as in the numerous transitions occurring from the release to the run-out. In addition, the snowpack conditions in the release zone and along the path, as well as the morphology of the avalanche paths, vary widely, rendering the avalanche dynamics, and consequently its modeling, a very difficult issue.
Despite this complexity, several simple models were proposed during the 20th century to capture the main features of snow avalanches (Reference HarbitzHarbitz, 1998). The majority of the models focused on the dense flowing part. One of the first models was proposed by Reference VoellmyVoellmy (1955). In this one-dimensional (1-D) model, the avalanche is considered as a sliding snow block submitted to the sum of a Coulomb friction and a dynamic drag proportional to the square of the velocity and inversely proportional to the flow depth. Using similar assumptions, several other authors (e.g. Reference HarbitzHarbitz, 1998) developed various models that predict velocities along the path and run-outs of the center of mass of the avalanche.
To account for flow depth variations in time and space during an avalanche event, the hydraulic framework has been adopted and a second generation of models, based on depth-averaged hydraulic equations, has emerged (Reference Kulikovskii and EglitKulikovskii and Eglit, 1973; Reference SavageSavage, 1979; Brugnot and Pochat,1981; Reference Bartelt, Salm and GruberBartelt and others, 1999; Reference Barbolini, Gruber, Keylock, Naaim and SaviBarbolini and others, 2000; Reference Naaim, Naaim-Bouvet, Faug and BouchetNaaim and others, 2004; Reference Buser and BarteltBuser and Bartelt, 2009). These models usually include a Voellmy-like, two-parameter friction model, as well as some additional parameters accounting for curvature, erosion and deposition processes and for the anisotropy of normal stresses. In addition to the velocity of the center of mass and run-outs, this second class of models allows the prediction of the flow depth along the path, as well as the deposition depth. These models have been developed in one and two dimensions by numerous authors, and some have been used to back-analyze spontaneous or artificially released snow avalanches in instrumented test sites (Reference Bartelt, Salm and GruberBartelt and others, 1999; Reference Naaim, Faug, Naaim and EckertNaaim and others, 2010).
Both the sliding-block and the hydraulic models require the specification of values for the friction parameters. Since the physics of flowing snow remains poorly documented and no direct rheological measurements exist, an empirical calibration is needed. Reference Buser and FrutigerBuser and Frutiger (1980) first inferred a pair of parameter values and the associated inter-event variability from ten extreme avalanches in Switzerland, with the idea of evaluating avalanche hazard on undocumented paths. Later, the pioneering experimental work of Reference Casassa, Narita and MaenoCasassa and others (1991) showed that the total friction of laboratory-made snow in a shear cell can be expressed as the sum of a constant term and of an increasing function of the velocity. This latter term can be approximated by a linear or parabolic function. Moreover, they found that the constant term is an increasing function of the snow temperature.
Since then, many authors have proposed deterministic (Reference Ancey, Meunier and RichardAncey and others, 2003) or stochastic (Reference Meunier, Ancey and NaaimMeunier and others, 2001; Reference Ancey, Gervasoni and MeunierAncey and others, 2004) calibration methods to infer friction coefficient values from a set of well-documented spontaneous events (Reference Ancey and MeunierAncey and Meunier, 2004) and/or artificially triggered avalanches (Reference Meunier, Ancey and TaillandierMeunier and others, 2004). Among them, Bayesian approaches have recently been the subject of growing interest (Reference AnceyAncey, 2005; Reference Straub and Gret-RegameyStraub and Gret-Regamey, 2006; Reference Eckert, Parent, Naaim and RichardEckert and others, 2008a; Reference Gauer, Medina-Cetina, Lied and KristensenGauer and others, 2009), because of their ability to quantify the related uncertainty with relatively simple simulation-based algorithms. Avalanche models of increasing complexity have been used, ranging from simple sliding blocks with a single Coulomb-like friction parameter (Reference Eckert, Parent and RichardEckert and others, 2007) to depth-averaged models with a two-parameter Voellmy friction term (Reference Eckert, Naaim and ParentEckert and others, 2010a). Often, the predominant ideas were to (1) infer the joint distribution of the friction parameters, (2) perform statistical/numerical Monte Carlo-like simulations to evaluate realistic run-out distance, Froude number and pressure distributions in a risk zoning perspective (Reference Barbolini and SaviBarbolini and Savi, 2001; Reference Meunier and AnceyMeunier and Ancey, 2004; Reference Eckert, Parent, Faug and NaaimEckert and others, 2008b) or (3) design defense structures (Reference Naaim, Faug, Naaim and EckertNaaim and others, 2010).
The relation between the friction coefficients and environmental variables has been investigated in several studies. The most noticeable results are the significant negative correlation between the constant single parameter of a Coulomb-like model and avalanche volume, highlighted by Reference AnceyAncey (2005), and the correlations between the constant parameter of Coulomb and Voellmy friction terms and release altitude and flow depth reported by Reference Eckert, Parent and RichardEckert and others (2007, Reference Eckert, Parent, Faug and Naaim2008b, Reference Eckert, Parent, Faug and Naaim2009, Reference Eckert, Parent, Kies and Baya2010b). In these latter papers, these correlations often indicate lower friction for greater sliding-block size/higher flow depth and for higher starting elevation. Nevertheless, these correlations varied strongly from one path to another, and even, for a given path, from one propagation model to another. This can possibly be explained by the very small sample size, since most of the studies included events recorded at a single path. This approach had the advantage of avoiding the difficulties faced while pooling data from different paths, but, with the exception of Reference AnceyAncey (2005) who used 173 avalanches from 7 paths, it precluded a firm conclusion regarding the significance and general meaning of the highlighted correlations between friction parameters and control variables.
Hence, since Reference Casassa, Narita and MaenoCasassa and others (1991), no systematic analysis of the influence of the physical properties of snow on friction has been undertaken. The objective of this paper is to explore the possible correlations between the friction parameters of snow involved in dense avalanches and the physical properties of snow, such as temperature, density and liquid water content, using a large set of past events, supplemented by a comprehensive set of snow and weather covariates. To this end, an avalanche dynamic model using a distributed snow depth and cohesion dataset issued from the chain of models SAFRAN/Crocus/MÉPRA (Reference Durand, Giraud, Brun, Mérindol and MartinDurand and others, 1999) as initial conditions has been calibrated for over 735 well-documented historical events from Chamonix valley, France. The observed run-out altitudes served as the criterion to calibrate the corresponding friction coefficients. The SAFRAN/Crocus chain also provides the altitudinally distributed snow temperature, snow density and snow liquid water content. In the following sections, we present the methodology and the results of the calibration of the dynamical model. We then address the existence of correlations between the calibrated friction coefficients and the parameters of the snow.
Avalanche Historical Data
The Chamonix valley extends for ∼23 km in the northernmost parts of the French Alps (Fig. 1). It is drained by the river Arve. Oriented along a southwest to northeast axis, it is bordered in the northwest by the Aiguilles Rouges massif, with elevations up to 2965 m a.s.l., and in the southeast by the Mont Blanc massif, which peaks at 4810 m a.s.l.

Fig. 1. Extensions of avalanches in Chamonix valley: data from avalanches.fr (Irstea) and topographic background from geoportail.fr (IGN).
‘Due to the abundance of snow storm at Le Tour, on January the 30th 1634 around 11 p.m., an avalanche destroyed completely nine houses and five barns,’ wrote Louis de Chone, director of the priory of Chamonix. Over 350 years later, on 9 February 1999, an avalanche from Pe’clerey mountain reached the hamlet of Montroc, devastating 17 chalets and killing 12 people (Reference Ancey, Rapin, Martin, Coléou, Naäm and BrunotAncey and others, 2000; Reference Rousselot, Durand, Giraud, Merindol and DanielRousselot and others, 2010). Two days later, the avalanche of Taconnaz overtopped the largest defense structure ever built in France (Reference Naaim, Faug, Naaim and EckertNaaim and others, 2010). These events clearly show how much remains to be done in the field of risk prevention in this area. The development of the Chamonix valley as a tourist center has been undertaken under the permanent threat of natural snow avalanches. Besides the iconic character of this valley, it is the historical depth and the amount of information available that has motivated the choice of this area for the present study, for which a sufficiently documented database is a prerequisite.
Around 115 avalanche corridors have been identified and monitored for ∼100 years by the Enquête Permanente sur les Avalanches (EPA; permanent avalanche survey) in the Chamonix valley. Some of them, like Taconnaz and Brevent, are very well known (Reference Naaim, Faug, Naaim and EckertNaaim and others, 2010). The number of events per path ranges from 5 to 100, and the observation period ranges from 50 to 100 years. The common use of this data is for risk assessment at the path scale (Reference Meunier, Ancey and NaaimMeunier and others, 2001; Reference Ancey, Gervasoni and MeunierAncey and others, 2004; Reference Eckert, Parent, Naaim and RichardEckert and others, 2008a, Reference Eckert2012), but regional approaches have also been undertaken recently (Reference Eckert, Parent, Kies and BayaEckert and others, 2010b). In addition to the date and the starting and run-out altitudes, additional data related to the meteorology and damage are also recorded, but are not used in this study.
In the EPA chronicle, each surveyed path has a predefined threshold altitude. When an avalanche reaches or passes this, it is considered to represent a significant threat and its characteristics are recorded. Hence, only medium and large avalanches are considered. More precisely, when an avalanche reaches the threshold altitude, a forest officer from the National Forest Office evaluates its release and run-out altitudes using binoculars and a topographic map, where several referenced geographic points are reported. Since 1965, the maps used have had a scale of 1 : 2500 with 10 m contours. The resulting average uncertainty in altitude may be estimated as ±15 m. Although the data collection protocol has seen several changes, including a major update in 2002, its philosophy has remained similar over the last few decades, to ensure reasonable homogeneity of the data series. Furthermore, mainly spontaneous avalanches are recorded in the EPA chronicle, and the few data from artificial or accidental triggers are excluded from our analysis. Note also that the EPA paths are insignificantly affected by the construction of recent countermeasures. This has been checked for the entire database (Reference Eckert, Baya and DeschatresEckert and others, 2010c), and it is assumed here that it remains true at the smaller spatial scale of the Chamonix valley.
In this study, we focus on the 26 best-documented paths, for which the following conditions are fulfilled: (1) continuous observation, (2) only few obviously erroneous data and (3) >20 events. These paths are listed in Table 1. Only avalanches since 1958 have been used, and obviously erroneous data have been removed. In paths where defense structures have been built (e.g. Taconnaz and Bourgeat paths), data since the construction have also been removed. In total, 735 events are included in our analysis.
Table 1. Avalanche paths considered in this study

Back-Analysis Toolboxes
The avalanche dynamic model used in this study is based on shallow-water equations. It takes into account erosion and deposition processes. We adopted the simple classical frictional model of Reference VoellmyVoellmy (1955). The topography is represented by 1-D longitudinal and transverse profiles built from an accurate digital elevation model using GIS software.
Terrain representation
The geomorphic and hydrologic processes that shape the morphology of avalanche paths are mostly driven by gravity. In steep terrains, because gravity prevails, it is therefore reasonable to assume that the flow is mainly 1-D. Although more or less pronounced local curvatures may be encountered, the intersection of the surface of the terrain with the vertical plane issued from the starting zone in the direction of slope orientation (aspect) is often the main axis of the avalanche thalweg. In this paper, avalanche paths are reduced to their longitudinal 1-D topographic profiles, i.e. the thalweg curvilinear profiles noted z(x), where z is the altitude and x the horizontal distance cumulated along the curvilinear profile. This profile is used to determine the local slope and the longitudinal curvature, C. Orthogonally to the longitudinal profiles, the shape of transverse profiles is approximated by a parametric power-law relationship between the flow thickness, h, and the flow half-width, y: y = knhn
−1. This approximation allows us to link the wetted surface, S, and the thickness of the flow, h, by the relationship S = 2khn
. The hydraulic radius, R, is defined as the ratio of S to the wetted perimeter, P. P is computed numerically by integration of ![]() . By varying the values of k and n (n > 1), a wide range of cross-sectional shapes can be represented, from triangular to quasi-rectangular.
. By varying the values of k and n (n > 1), a wide range of cross-sectional shapes can be represented, from triangular to quasi-rectangular.
All the available geographic data have been aggregated in a single information system, which uses the functionalities of the open-source GIS, GRASS (Geographic Resources Analysis Support System). In particular, we have integrated a summer digital terrain model (DTM), achieved through aerial laser scan technology, with a resolution of 1 m. This DTM covers the entire Chamonix valley area. It was supplemented, when necessary (especially for high altitudes and glacial areas), by a 25 m DTM provided by the Haute Savoie departmental data service (RGD 74). The chronology of avalanches, imported from the French avalanche chronicle (EPA), and the extensions of extreme historical avalanches from the French avalanche atlas (Carte de Localisation des Phénomènes d’Avalanches (CLPA)), were also integrated into the information system. For the 26 studied paths, the longitudinal and cross-wise profiles were constructed. The longitudinal profiles were obtained from the intersection of the main avalanche thalweg with the DTM surface. An example of a longitudinal profile together with the historical run-out altitudes is shown in Figure 2. The transverse profile locations were defined manually, in order to capture the main changes in path morphology. For each of these transverse profiles, the parameters n and k were determined by nonlinear adjustment (Fig. 3).

Fig. 2. Example of topographic profile and historical starting (red full circle) and run-out (blue empty circle) altitudes (Taconnaz path).
For the numerical simulations, the longitudinal profiles were then projected onto a regular grid of constant cell size, Δx. At each point of the grid, the curvatures and slopes were calculated directly from the DTM. The parameters n and k were linearly interpolated on the regular grid.

Fig. 3. Transverse profile example and adjustment by a power-law relationship.
Model equations
Since, for medium to large dense snow avalanches, the ratio of the depth, h, to their length, L, is small enough (h/L ≪1), the shallow-water formalism holds (Reference SavageSavage, 1979; Reference Gray, Wieland and HutterGray and others, 1999; Reference Pudasaini and HutterPudasaini and Hutter, 2007). The dynamics of the avalanche are governed by the conservation of mass and momentum. The equations system can be written as

where U is the average velocity over section S, θ the local slope angle, t the time, x the curvilinear horizontal abscissa, g the gravitational acceleration, φ the entrained or deposited snow flux and μ the total friction coefficient.
The velocity profiles obtained from existing in situ measurements or chute experiments (e.g. Reference Nishimura and MaenoNishimura and Maeno, 1987; Reference Dent, Burrell, Schmidt, Louge, Adams and JazbutisDent and others, 1998; Reference Bouchet, Naaim, Bellot and OussetBouchet and others, 2004; Reference Rognon, Roux, Naäim and ChevoirRognon and others, 2007; Reference Kern, Bartelt, Sovilla and BuserKern and others, 2009) show linear-piecewise shapes. The shear, and consequently the resulting dissipation, are mainly located at the interface between the moving snow and the snow (or the soil) at rest at the base of the flow. The depth average of the square of the velocity can consequently be approximated by the square of the average mean velocity ![]() , which leads to κ ≈ 1 in Eqn (1).
, which leads to κ ≈ 1 in Eqn (1).
In this framework, we adopted a simple Coulombian friction model, i.e. the shear stress along the slope is assumed to be proportional to the normal stress. The proportionality coefficient is given by the standard two-parameter model of Reference VoellmyVoellmy (1955): the total friction coefficient, μ, is the sum of a static friction coefficient, μ
o, and a dynamic drag coefficient, gF
2
/ ξ, where ![]() is the Froude number and ξ (m s−2) the inertial friction coefficient.
is the Froude number and ξ (m s−2) the inertial friction coefficient.
Concerning the mass balance, the formalism developed by Reference Naaim, Naaim-Bouvet, Faug and BouchetNaaim and others (2004) was used to determine the mass exchange conditions and entrained or deposited depth, δ, between the moving snow and the snow at rest. Erosion and entrainment occur if

where τ c is the cohesion of the snow at rest. Deposition occurs if
The exchanged snow depth between the moving snow and the snow at rest during a time-step, Δt, is

where p is a power-law index used to approximate the constitutive relationship of snow near the base of the flow (p ≈ 0.1). The hyperbolic system of Eqns (1) and (4) is solved numerically using an explicit and accurate second-order Godunov–Van Leer scheme (Reference VilaVila, 1986). To guarantee the stability and the convergence of the numerical scheme, the time-step is kept under the Courant–Friedrichs–Lewy threshold.
Snowpack conditions on dates of avalanche occurrences
The avalanche dynamics model requires, as an input, accurate knowledge of the altitudinal distribution of snow-cover characteristics (depth, stratification, cohesion) at the date of each simulated event and for each path. However, the characteristic length of the valley and of the massif is ∼23 km, and the vertical drop of the paths studied is generally >2 km. Clearly, no operational network currently exists that would allow, over such a large area, knowledge or reconstruction of the snow cover and of its structure at the spatial scale of an avalanche path and at an hourly timescale, especially in times of imminent release of medium to large avalanches.
To overcome the lack of a homogeneous and daily record of the snow conditions at the relevant altitudes over the entire period covered by the present study, the vertical profiles of the physical properties of the snowpack used as input to the avalanche dynamics model were computed using the SAFRAN/Crocus/ME’PRA (SCM) model chain. SCM has been used for two decades in operational avalanche hazard prediction activities operated by Me’te’o-France, and has been used for many evaluation and application studies in the French mountain regions (Reference Durand, Laternser, Giraud, Etchevers, Lesaffre and MérindolDurand and others, 2009a,Reference Durand, Giraud, Laternser, Etchevers, Mérindol and Lesaffreb; Reference Rousselot, Durand, Giraud, Merindol and DanielRousselot and others, 2010; Reference Castebrunet, Eckert and GiraudCastebrunet and others, 2012). SAFRAN is a meteorological downscaling model which combines a priori information from a large-scale numerical weather prediction model with in situ and radiosonde observations, to provide the best possible estimate of the ground meteorological conditions in French mountain regions (Reference Durand, Brun, Mérindol, Guyomarc’h, Lesaffre and MartinDurand and others, 1993, Reference Durand, Giraud, Brun, Mérindol and Martin1999). SAFRAN operates at the scale of geographical zones assumed to be meteorologically homogeneous (referred to as ‘massifs’), within which meteorological variables depend on time and elevation. The ‘Mont Blanc’ SAFRAN massif encompasses the whole Chamonix valley, so only data from this massif were used for the present study. SAFRAN was run from 1958 to 2013 using large-scale meteorological fields from the European Centre for Medium-Range Weather Forecasts’ ERA-40 global analysis (Reference Durand, Laternser, Giraud, Etchevers, Lesaffre and MérindolDurand and others, 2009a,Reference Durand, Giraud, Laternser, Etchevers, Mérindol and Lesaffreb), and therefore provides an hourly estimate of meteorological conditions in the Chamonix valley over elevation levels in steps of 300 m for the whole study period. These SAFRAN data were used to run the detailed snowpack model Crocus (Reference Brun, Martin, Simon, Gendre and ColéouBrun and others, 1989, Reference Brun, David, Sudul and Brunot1992), which simulates the evolution over time of the vertical profile of the physical properties of snow under given meteorological driving data. The variables simulated by Crocus are, for each of the variable number of numerical layers used: snow temperature, density, liquid water content, grain shape and size (Reference Brun, David, Sudul and BrunotBrun and others, 1992). Due to the strong impact of the radiative budget of the snowpack on its time evolution, for each altitude level simulations were carried out for a slope of 40° and six aspects (N, E, SE, S, SW, W) (Reference Durand, Giraud, Brun, Mérindol and MartinDurand and others, 1999). Finally, Crocus outputs were fed to the ME’PRA model to diagnose the physical state of the simulated snowpack in terms of mechanical properties (Reference Durand, Giraud, Brun, Mérindol and MartinDurand and others, 1999).
In this work, for each avalanche since 1958, we extracted the snow depth, h s, and the burial depth of the weakest layer, h f, from the reconstructed data provided by the SCM chain. This latter quantity is a standard output of ME’PRA, inferred from the vertical profile of snow density and grain type computed by Crocus. As an approximation, the snowpack was then decomposed into two parts: one above the weakest layer, and one below. For each of these parts, we extracted the average snow density, ρ, the average temperature, T, the average liquid water content, ρ w, and the shear strength, τ c. For each event, defined by its date and the main aspect of the path, these data were generated for each 300 m slice from 900 up to 3100 m altitude (Fig. 4). These data were then linearly interpolated over the simulation grid.

Fig. 4. Two examples of snow depths and snow properties altitudinal distributions along a given path (Lyapet path) for two dates corresponding to two recorded avalanches. (a) Snow depth, h s. The dashed area represents the zone above the weakest layer. (b) Temperature, T, averaged over the entire snow depth. (c) Density, ρ, averaged over the entire snow depth. (d) Liquid water content, ρ w, averaged over the entire snow depth.
This approach, relying on snowpack data for each event at the scale of the Mont Blanc meteorological massif, is justified by the following two arguments. First, the characteristic lengths of the Chamonix valley and of the Mont Blanc meteorological massif are the same, such that the two zones can be regarded as identical. Second, the avalanches considered in this study are of medium to large magnitude. They generally result from large-scale meteorological perturbations. In such situations, the snow precipitation can be considered homogeneous at the scale of the considered area. Hence, even if this clearly represents a rough approximation, we expect that the snow mobilized by the avalanche, mainly consisting of recent precipitation, is also homogeneous at the scale of the massif.
Friction Coefficient Inference
The studied avalanche paths have large elevation drops. The snow parameters thus vary all along these paths. The avalanche erodes and incorporates snow from the start to the run-out zones. We may therefore expect that the frictional properties change along the covered distance. In addition, the avalanches involve mechanical and thermodynamical transformations and energy dissipation that may change the mechanical and thermodynamic properties of flowing snow (Reference Buser and BarteltBuser and Bartelt, 2009). Accounting for all these complex processes in propagation models is currently out of reach. Moreover, the calibration and validation of such models would require in situ measurements all along the path. Since the only consistently available data are the start and run-out altitudes, and given the current state of knowledge, we considered that the most suitable approach was to treat the avalanche as an average process and to work only with average effective parameters for the friction as well as for the snow-cover properties.
To infer the friction coefficients of the 735 events that took place within the 26 paths, we proceeded as follows. The starting altitude of each event is known. The starting area is then taken as the largest zone of homogeneous slope angle including the starting altitude. The fracture depth is limited to the snow depth above the weakest layer. Afterwards, the avalanche accelerates and, according to the stress applied on the snow at rest, may entrain the snow above the weakest layer or the whole snow cover, according to the erosion and deposition model described in Eqn (4). The run-out altitude, which is used here as the calibration criterion, is known. We thus have all the information needed to infer the friction parameters, with the assumption that the two friction coefficients are constant along the path for each event. The problem faced here is an inversion problem. The adopted inference procedure is achieved in three steps. We scanned the entire range of the static friction parameter, μ o, from 0.1 to 0.7 in steps of 0.01, and the entire range of the inertial friction coefficient, ξ , from 500 to 1500 m s−2 in steps of 50 m s−2. For each pair (μ o, ξ), a numerical simulation was performed and the corresponding run-out altitude was determined. The difference between this and the observed altitude was then calculated. All pairs of parameters for which this difference was lower than ±15 m were retained, and their averages and standard deviations were calculated for each avalanche. In total, 941 535 simulations were performed. The simulation campaign took 2890 CPU-hours on a 12-processor parallel computer.
As shown in Figure 5, the difference between the calculated and observed run-out altitudes is a monotonic function of the static friction coefficient, μ o. As a consequence, the inference of μ o systematically yields a well-constrained value for this parameter, within the ranges of uncertainty linked to the data and to the discretization of the parameter range. This is illustrated in Figure 6, in which the distribution of the standard deviation of admissible μ o values shows a highly pronounced peak at zero. For >90% of the events, the value of μ o is resolved with an accuracy less than three times the discretization step.
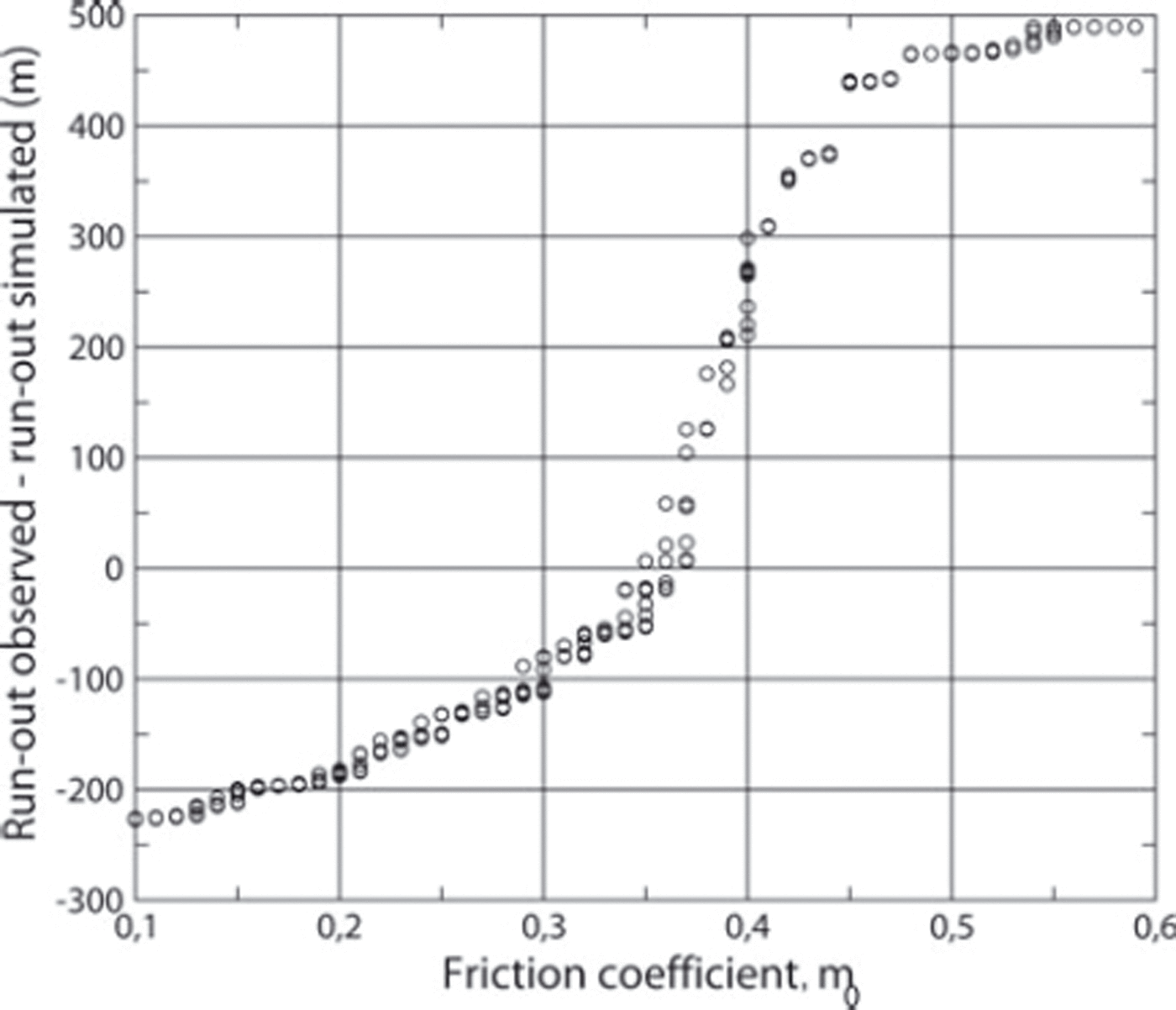
Fig. 5. Example of evolution of the difference between observed and simulated run-out altitudes as a function of the static friction coefficient, μ o, for one of the back-analyzed events.

Fig. 6. Distribution of standard deviations of inferred values of the static friction coefficient, μ o, for each back-analyzed event.
The case for ξ is slightly less clear. For most of the events, the difference between the calculated and observed run-out altitudes is also a monotonic function of this parameter, and the inference then yields a well-defined and accurate value of ξ (Fig. 7). Hence, for ∼80% of the events, the value of ξ is resolved with an accuracy less than three times the discretization step. However, there are also cases, typically when the slope angle of the run-out zone is small, for which ξ has almost no influence on the run-out altitude. For these cases, which represent ∼20% of our dataset, the adopted inversion criterion based on the run-out altitude only, is not sufficient to discriminate between ξ values. This corresponds to the secondary peak in the distribution of the standard deviations in Figure 7. This peak is at a value of ∼300 m s−2, which corresponds to the standard deviation of a random variable uniformly distributed over the whole range of ξ: ![]() .
.
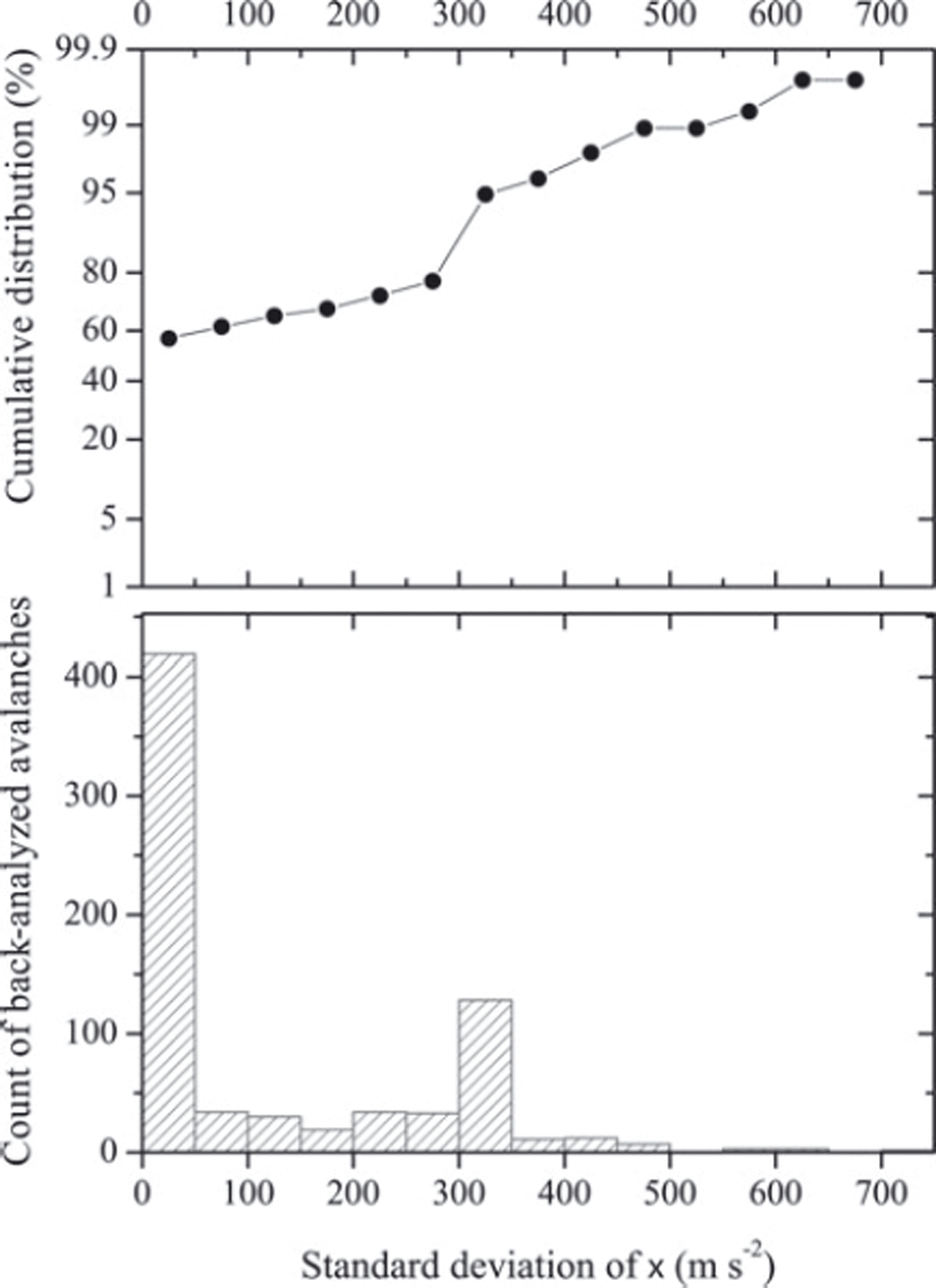
Fig. 7. Distribution of standard deviations of inferred values of the inertial friction coefficient, ξ, for each back-analyzed event.
Correlations With Snow Properties
As described in the previous section, for each event we averaged the snow physical properties (temperature, density and liquid water content), first on the snow depth and then between the starting and run-out altitudes. We also averaged the snowpack depth between the starting and run-out altitudes. The set of obtained inertial friction coefficients was then analyzed, in order to highlight possible trends with these average snow physical properties.
Inertial friction coefficient
For the analysis of inertial friction coefficient data, only events for which the value of ξ is reliably determined (i.e. ∼80% of the events) were retained. As shown in Figure 8, no obvious linear trend is observed between the inertial friction coefficient, ξ, and the average temperature, density or liquid water content. The average value of ξ obtained from the entire simulation campaign is 940 m s−2, with a standard deviation 220 m s−2.

Fig. 8. Back-analyzed values of inertial friction parameter, ξ, vs (a) average snow density (correlation coefficient R 2 = 3 × 10−5), (b) average snow liquid water content (R 2 = 6 × 10−5) and (c) average snow temperature (R 2 = 2 × 10−4).
Static friction coefficient
For each path, the possible correlations between the calibrated static friction coefficients, μ o, and the corresponding average snowpack physical properties have been studied using the stepwise method and principal component analysis. In some paths significant trends were observed. For instance, the temperature and the liquid water content were observed to have a significant influence on the static friction coefficients in five paths, whereas an influence of the average snowpack depth over the whole covered area was evidenced in 13 paths. However, it has not been possible to infer trends common to all the studied paths. This confirms the difficulty mentioned in the Introduction in inferring systematic correlations between friction parameters and snow physical properties with only the limited amount of data recorded in one path.
We then grouped all the data and analyzed the influence of density, liquid water content and temperature on this composite dataset. As shown in Figure 9, it was difficult to infer significant relations capturing the full data variability well. Possible explanations for these somewhat deceptive results are discussed below. Furthermore, the full dataset involves a large number of data corresponding to frequent snow characteristics, whereas avalanches involving snow with extreme properties are, by definition, rare. Consequently, we found it useful to resample the dataset into 9–14 classes of equal amplitude, but unequal repartition (for each class, the mean and the standard deviation of the static friction coefficient, μ o, were calculated). This better covers the full ranges of observed snow physical properties, giving more weight to rare events, which were searched for. However, the drawback of the approach is that little can be said about the statistical significance of the evolution of μ o with the three variables presented and discussed hereafter. Hence, at this stage, our objective is essentially to highlight physical trends.

Fig. 9. Full dataset of back-analysed static friction coefficients, μ o, as a function of (a) average snow density, ρ, (b) average snow liquid water content, ρ w, and (c) average snow temperature, T. (c) also shows the linear fit of the full dataset (solid blue line, determination coefficient R 2 = 0.1) and the fit obtained by Reference Casassa, Narita and MaenoCasassa and others (1991) (dashed magenta line).
Correlation with snow density
Twelve classes of snow density, ranging from 100 to 450 kg m−3, have been defined. The data are reported In Figure 10. An important remark concerns the rarity of events involving light or heavy snow: the proportion of events with snow of density ≤150 kg m−3 is <9% of the set, and the proportion of events involving snow of density ≥350 kg m−3 is <5%. Concerning the mean static friction coefficient, μ o, no trend with snow density is observed for density values >200 kg m−3. For lower values, however, the mean static friction coefficient appears to behave as an increasing function of the snow density. The mean friction coefficient, μ o, reaches a value as low as 0.17 fora density of 113 kg m−3.
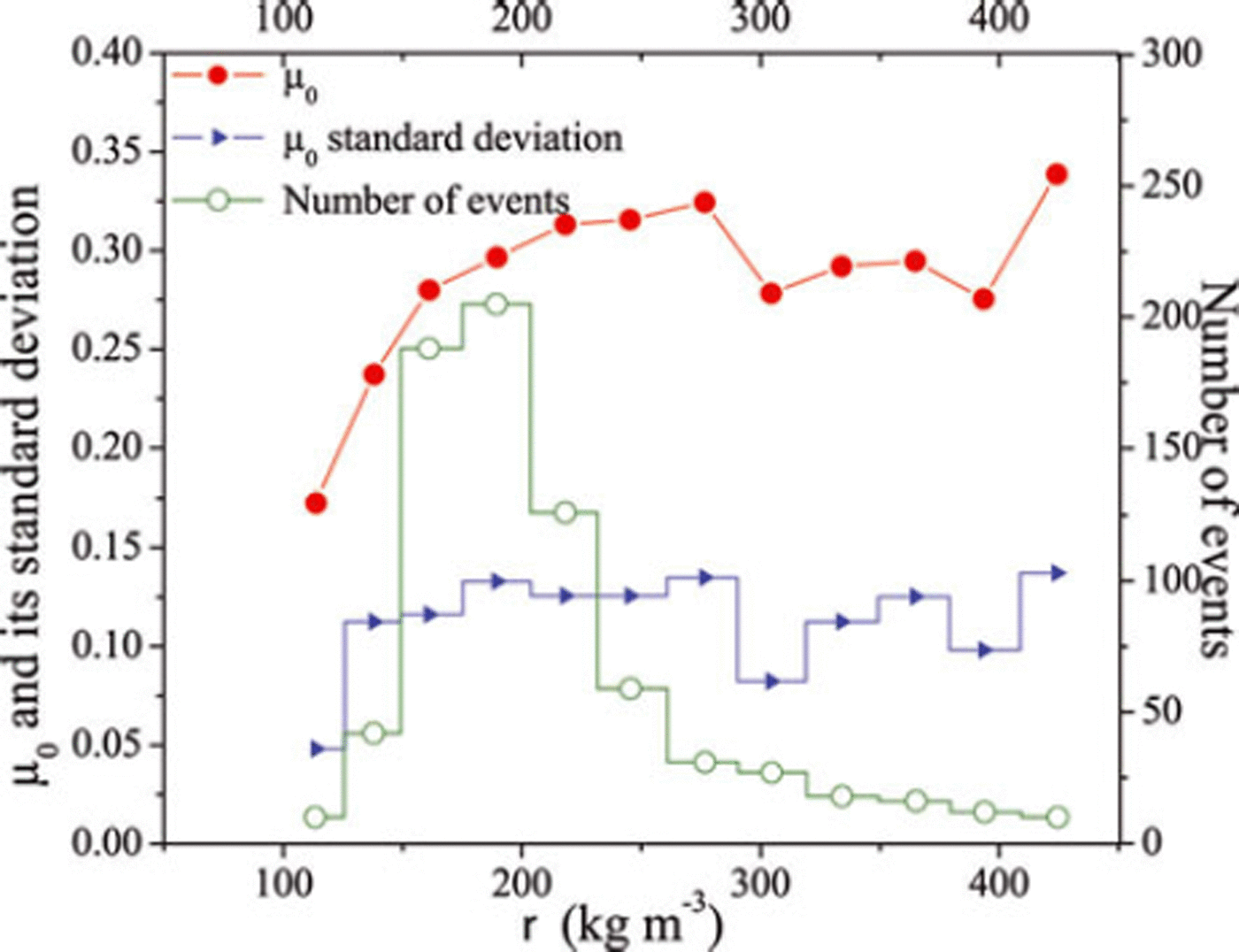
Fig. 10. Class averages and standard deviations of back-analyzed static friction coefficients, μ o, as functions of average snow density.
Correlation with liquid water content
Fourteen classes of liquid water content have been defined. The data are displayed in Figure 11. The first remark is that 43% were dry avalanches (i.e. avalanches for which the liquid water content is zero) and 57% wet avalanches. The second remark is that no trend between the mean static friction coefficient, μ o, and the total liquid water content is observed for low to moderate values of this parameter, typically <35 kg m−3. For higher values of the liquid water content, the mean static friction coefficient decreases strongly and reaches 0.16 for a liquid water content of 40 kg m−3. This abrupt change probably marks the beginning of the transition towards slush flows.

Fig. 11. Same as Figure 10, but as functions of average snow liquid water content.
Correlation with snow temperature
For the temperature, 12 classes of equal amplitude (1 K) were defined. The data are displayed in Figure 12. For the three lower temperature classes, the number of events per class is only 5, while the number of events in the highest temperature class is 240. We observe that the mean static friction coefficient increases quasi-linearly with temperature. This evolution is stronger than those highlighted with density and liquid water content, as it is observed over several classes involving a large number of avalanches. Interestingly, it is consistent with the snow shear-cell experiments of Reference Casassa, Narita and MaenoCasassa and others (1991). Those authors proposed the following linear function to describe their results: μ o = 0.47 + 0.01(T − 273.15), while the data obtained here can be adjusted by μ o = 0.33 + 0.011(T − 273.15) (determination coefficient R 2 = 0.84). Hence, the slope found by Reference Casassa, Narita and MaenoCasassa and others (1991) and that exhibited by our data are essentially the same (∼0.01K−1), while the offsets appear to differ.

Fig. 12. Class averages (blue circles) and standard deviations (red triangles) of back-analyzed static friction coefficients, μ o, as functions of average snow temperature, T. The number of events for each class is also shown (green diamonds). We also plotted our best fit (dashed blue line), the experimental data of Reference Casassa, Narita and MaenoCasassa and others (1991) (magenta circles) and their fit (dashed magenta line).
In addition, the linear function inferred from the class averages is also significant for the full dataset (intercept and trend are nonzero at the 5% significance level), but obviously with a lower determination coefficient (R 2 ≈ 0.1), due to the much greater scattering of back-calculated friction parameters with regard to class averages (Fig. 9c). This result gives additional credit to the chosen approach relying on class analysis.
This trend with the temperature is also consistent with the larger-scale results of Reference Eckert, Baya and DeschatresEckert and others (2010c, Reference Eckert, Keylock, Castebrunet, Lavigne and Naaim2013), which suggest that the large upslope retreat of mean and large-magnitude run-outs in the French Alps over the 1985– 2000 period is partially attributable to the strong concomitant atmospheric warming that modifies the average characteristics of snow, in addition to its influence on snow-cover reduction.
Discussion and Conclusions
The calibration of a two-parameter hydraulic avalanche dynamics model has been performed on 735 historical avalanches that have occurred in the Chamonix valley since 1958. All the avalanches reached a predefined altitudinal alert threshold, which constitutes a necessary condition to be recorded in the French avalanche chronicle. The magnitude of these avalanches can be considered as moderate to large. Meteorological conditions in the valley, especially during avalanche periods, have been considered homogeneous and the initial conditions of the model were extracted from the reconstructed snowpack data computed with the SCM chain model. The ranges of the two friction parameters were scanned and the best pairs (ξ, ξ) were determined for each event. The run-out altitude served as a criterion to calibrate these two friction parameters. The correlations of the obtained friction parameters with three available snow properties, namely density, temperature and liquid water content, were searched for.
We found no apparent trends or correlations between the inertial coefficient, ξ, and the snow physical properties. An average value, ξ = 940 m s−2, was inferred with a standard deviation of 220 m s−2, which could be used in further statistical/dynamical simulations in this area. However, for the static friction coefficient, μ o, this study found qualitative (i.e. after class averaging) but strong (i.e. relative to a large number of rather high-magnitude events recorded on active avalanche paths) evidence of dependency between the avalanche friction parameter and snow physical properties. Some of these trends confirm previous findings, whereas others are new contributions to our understanding of snow in motion. They may well be worth taking into account when refining avalanche simulations to include various snow and weather situations.
Our main result is the linear increase of the mean static friction coefficient with temperature and density, although, for the latter case, the trend is observed only for density values <200 kg m−3. This increase confirms how dangerous avalanches involving light and cold snow are. They can cover very large distances, even with moderate volumes of snow, as observed during the catastrophic winter of 1999, when several avalanches overpassed their known historical extensions. The trends also give more weight to the larger spatiotemporal scale approaches, having recently evidenced higher-magnitude avalanches during colder winters (Reference Eckert, Naaim and ParentEckert and others, 2010a, Reference Eckert, Keylock, Castebrunet, Lavigne and Naaim2013).
Another important result concerns the case of wet snow avalanches. It appears that the liquid water content has no significant effect, except for high values ρ w > 35 kg m−3, for which the static friction coefficient decreases significantly and may reach similar values to those obtained at very low temperatures.
Also interesting is the good agreement found between the correlation of the static friction coefficient with temperature derived from this study, and that obtained by Reference Casassa, Narita and MaenoCasassa and others (1991) from their experiments. This agreement suggests that the friction coefficients derived from avalanche back-analysis can be regarded as representative of true rheological parameters of snow. The discrepancies in offset noted in Figure 12, which remain on the order of magnitude of the standard deviation value, can presumably be explained by an influence of snow type or grain/aggregate size (scale effects).
Finally, we studied the correlations between the mean static friction coefficient, μ o, and the average snow depth. Similarly to the previous analyses, classes of depths were defined (Fig. 13). Globally, events mobilizing large amounts of snow (h t ≥ 1.8 m) are rare: they represent <1.3% of the total number of events. We observe that, for large avalanches, the mean static friction coefficient decreases with the total snow depth. The trend can be approximated by the following linear function: μ o = 0:38 – 0.09h s for h s > 0:5 m (determination coefficient R 2 = 0.86). This reduction of friction with snow quantity is consistent with local expert knowledge, and with most of the existing results regarding correlation between friction parameters and snow physical properties (Reference AnceyAncey, 2005; Reference Eckert, Parent and RichardEckert and others, 2007, Reference Eckert, Parent, Faug and Naaim2008b, Reference Eckert, Parent, Faug and Naaim2009, Reference Eckert, Naaim and Parent2010a). It has often been interpreted as a scale effect. For instance, in the Swiss guidelines (BFF/SLF, 1984), the coefficient, μ o, for the Voellmy model is taken as decreasing with the avalanche volume, in agreement with findings regarding mass movements (Reference Dade and HuppertDade and Huppert, 1998; Reference Bartelt, Bühler, Buser, Christen and MeierBartelt and others, 2012). However, our results also show that low friction coefficients are systematically associated with low temperatures and densities or with high liquid water content. Hence, the dependence with snow depth and volume could also be due to the fact that large avalanches generally involve low-density snow at low temperatures in winter and snow with high liquid water content in spring.

Fig. 13. Class averages (red full circles) and standard deviations (blue full circles) of back-analyzed static friction coefficients, μ o, as functions of average snow depth. The number of events for each class is also shown (green empty circles).
Despite the general coherence of these results, several limits must be kept in mind. First, the level of uncertainty involved when manipulating field observations remains high. Second, the approximations and assumptions adopted for modeling both the dynamics of the avalanches and the reconstruction of the snowpack were numerous. For instance, the snow physical properties and friction coefficients were averaged over each path, which is a rough simplification of reality. Hence, the correlations obtained should be regarded as relevant only for average parameters at the scale of the path. Third, some possible effects specific to events recorded on each path were not considered (all inferred friction parameters were pooled). Finally, identifying a depth-averaged propagation model with a Voellmy friction law, i.e. the existence of a single solution of the inversion, is not simple; it depends on the data available on a given path and on its topography. Here it has been shown that, in most of the cases, the ±15 m criterion could be fulfilled. Nevertheless, no estimate of the calibration uncertainty could be obtained, since we did not specify any proper expression of the likelihood of the simulations with regard to the data. Consequently, it was not possible to consider this error in the inference of the relation with the snow physical properties. Going further may imply the inclusion of the calibration step within the regional analysis, bridging the works of Reference Lavigne, Bel, Parent and EckertLavigne and others (2012) and Reference Eckert, Parent, Kies and BayaEckert and others (2010b), in order to directly link the local friction parameters by their common dependence on snow physical properties. Taking into account the local effects in the statistical modeling may also be a fruitful direction for further work.
Acknowledgements
We thank the European Feder Fund, the Haute Savoie Department CG74 and the French National Research Agency (MOPERA project) for financial support. We are also grateful to the anonymous reviewers and to Perry Bartelt, whose contributions improved the paper, and to Gérald Giraud and Samuel Morin (CNRM-GAME/CEN) for their help in SCM model runs and interpretation. Irstea is part of labex OSUG@2020 and labex TEC21.
















