1. Introduction
Physicists have long been interested in the plasticity of ice. The first experiments seem to have been performed by Reference McConnel and KiddMcConnel and Kidd (1888) who showed that single crystals of ice plastically deformed like a pack of cards, and observed that the rate of deformation increased with time. The idea of the viscous behaviour of glacier ice was expressed by Reference RenduRendu (1840) and studied by L. Agassiz and J. D. Forbes between 1840 and 1851 (Reference TyndallTyndall, 1873).
More recently, interest in research on the plasticity of ice was significantly increased by the joint meeting of the British Glaciological Society (BGS) and the Institute of Metals held in Cambridge, UK, on 29 April 1948. Dr G. Seligman, past president of the Institute of Metals and awarded the Seligman Crystal in 1963, was the chairman of this meeting (BGS, 1949). E. Orowan and M.F. Perutz, both of the Cavendish Laboratory, Cambridge, opened the discussion on ‘The flow of ice and other solids’. Orowan is well known for his work on the plasticity of metals, especially on the role of dislocations in the plasticity of crystalline solids (Reference OrowanOrowan, 1940). Perutz, winner of the Nobel Prize in chemistry, was the PhD supervisor of J.W. Glen. Reference GlenGlen (1952) and Reference NyeNye (1952) showed that the viscosity of ice decreases with increasing stress, i.e. the creep of ice is non-Newtonian, as assumed by BGS (1949). It is worth noting that, at this time, most new ideas on ice plasticity came from the materials science community, while glaciology research had just begun.
Progress in understanding the plasticity of ice has since been achieved by creep experiments performed on ice single crystals and polycrystals. Evidence of easy basal slip was first shown by Reference McConnel and KiddMcConnel and Kidd (1888) and later by many authors (Reference Glen and PerutzGlen and Perutz, 1954; Reference Griggs and ColesGriggs and Coles, 1954;Reference SteinemannSteinemann, 1954; Reference Higashi and OuraHigashi, 1967; Reference Jones and GlenJones and Glen 1969; see Reference Weertman, Whalley, Jones and GoldWeertman, 1973, for a review). The flow law relating strain rate to the applied stress for basal slip in single crystals is a power law with a stress exponent of ~2 (Reference Higashi, Koinuma and MaeHigashi and others, 1965; Reference Jones and GlenJones and Glen, 1969; Reference Mellor and TestaMellor and Testa, 1969). Using the famous Orowan’s relation and measurements of the velocity of dislocations on the basal plane (Reference Petrenko and WhitworthPetrenko and Whitworth, 1999), the density of mobile dislocations could be determined.
Many creep experiments have been performed on isotropic freshwater ice at relatively high temperature in order to determine the flow law of glacier ice (Reference GlenGlen, 1955; Reference SteinemannSteinemann, 1958). Ice, like many other materials, exhibits three stages: an initial decelerating primary creep, a quasistationary secondary creep and finally a tertiary creep with a higher strain rate. A description and results of such experiments are provided by Reference JackaJacka (1984). The flow law for isotropic ice is also a power law, but with a stress exponent of ~3 for an equivalent stress higher than 0.1-0.2 MPa (Reference Barnes, Tabor and WalkerBarnes and others, 1971; Reference Budd and JackaBudd and Jacka, 1989). The behavior of ice at low stresses has been the subject of numerous studies over several decades. The difficulty of obtaining reliable data at strain rates lower than 10-10s-1 accounts for the contradictory results. There is a clear indication of decrease in the stress exponent as soon as equivalent stresses are <0.1 MPa (Reference Schulson and DuvalSchulson and Duval, 2009).
The effect of dynamic recrystallization and fabrics (or textures in materials science) on the behavior of ice is significant when looking at glacier dynamics. The effect of fabrics is now taken into account in ice-sheet flow modeling (Reference Martin, Gudmundsson, Pritchard and GagliardiniMartin and others, 2009; Ma and others, in press). Conditions for the occurrence of secondary and tertiary creep in polar ice sheets, however, are not very clearly determined. This deficiency comes from lack of knowledge of the physical conditions for the occurrence of continuous (rotation) or discontinuous (migration) recrystallization (Reference AlleyAlley, 1992; Reference Schulson and DuvalSchulson and Duval, 2009). Analysis of the effect of grain size, particles, impurities and water content on the ice viscosity is provided by Reference PatersonPaterson (1991) and Reference Schulson and DuvalSchulson and Duval (2009) for glacier ice and by Reference Durham, Kirby and SternDurham and others (1992) for ice of the outer Solar System.
These experimental results alone do not permit identification of the physical processes involved in the deformation of ice. As in metals, the gliding of dislocations on crystallographic planes is the main mechanism of the plastic deformation. Purely diffusional processes are invoked to explain the behavior of polycrystalline ice at low stresses, but the occurrence of such processes in ice is not proven. The n=3 stress exponent found in polycrystalline ice could, however, be explained by dislocation climb, which involves the diffusion of point defects (Reference WeertmanWeertman, 1983).
Dislocation-mediated plasticity is commonly considered as a regular process occurring homogeneously in space and smoothly in time. This viewpoint was challenged many years ago by Reference NakayaNakaya (1958) who performed bending experiments on ice single crystals. Traces of basal slip lines were made visible by shadow photography. Information about the temporal behavior of plastic flow has been inferred more recently from acoustic emission measurements on ice single crystals by Reference Weiss and GrassoWeiss and Grasso (1997). These experiments performed during deformation showed that plastic deformation proceeds through an intermittent dynamics. The intermittency of dislocation activity is associated with spatial localization because each strain burst appears to correspond to the formation of a slip line. Both acoustic emission experiments and analyses of the distribution of slip lines by X-ray topography on ice single crystals revealed scale invariance with power-law size distribution for strain bursts and scale-invariant (fractal) dislocation arrangements over several decades (Reference Miguel, Vespignani, Zapperi, Weiss and GrassoMiguel and others, 2001; Reference Weiss and MarsanWeiss and Marsan, 2003; Reference MontagnatMontagnat and others, 2006). Dislocations move cooperatively in groups rather than individually. This collective behavior is driven by long-range elastic dislocation interactions. In polycrystals, grain boundaries act as barriers to the dynamic propagation of dislocation avalanches and hinder this scale-free pattern (Reference Richeton, Weiss and LouchetRicheton and others, 2005b). These scale-invariant properties can raise difficulties for the use of average quantities (e.g. dislocation density) or homogenization techniques (Reference Weiss and MontagnatWeiss and Montagnat, 2007).
Understanding of the dynamics of interacting dislocations, still in its infancy, is of the highest importance for the behavior of crystalline materials. Following Reference MottMott (1953), primary creep in polycrystalline ice obeys the Andrade creep law in t 1/3. It can be analyzed by considering the long- range dislocation interactions and kinematic hardening induced by the strong visco-plastic anisotropy of the ice crystal (Reference Louchet and DuvalLouchet and Duval, 2009).
Computation of the mechanical behavior and texture development in polycrystalline materials using micro-macro techniques is now a standard approach in materials and geological science. The limitations of such approaches are related to the difficulty of considering stress and strain intragranular heterogeneities, especially in anisotropic materials. Full-field formulation based on fast Fourier transform (FFT) has recently been used to predict the micromechanical fields in polycrystalline ice (Reference Lebensohn, Montagnat, Mansuy, Duval, Meyssonnier and PhilipLebensohn and others, 2009). The very large visco-plastic anisotropy of the ice crystal induces strong deformation gradients and strain localization inside grains (Reference MansuyMansuy, 2001). A digital image correlation technique was recently used to record continuously the intragranular strain field during creep tests on columnar ice (Grennerat and others, in press). One objective of these experimental measurements is to validate a full-field FFT model treating the elasto/visco-plasticity, required to analyze transient effects.
Considering these recent experimental and modeling results, the contribution of the ice physics community to the theoretical understanding of the mechanical behavior of materials is significant. With the large anisotropy of the ice crystal, ice is now considered a model material for validating theoretical assumptions made in mechanical models (Reference Lebensohn, Tomé and Ponte CastanedaLebensohn and others, 2007). Ice lends itself to experimental analysis because of its transparency to visible light and X-rays, the ease with which large single crystals and two-/three-dimensional polycrystals with various grain sizes can be grown, the possibility of performing mechanical tests near the melting point and the preponderance of dislocations accommodating orientation gradients (excess dislocations) on forest dislocations (statistically stored dislocations) (Reference NyeNye, 1953; Reference AshbyAshby, 1970).
This paper summarizes the main mechanical properties of the single crystal and the polycrystal. We show that long- range dislocation interactions play a fundamental role in the plasticity of ice. Special emphasis is placed on the development of stress and strain-rate heterogeneities inside grains during primary creep. The role of long-range internal stresses in grain nucleation during discontinuous recrystallization is also discussed.
Following the seminal and fruitful discussions between glaciologists and metal physicists during the joint meeting held in Cambridge in 1948, we wish to show the high interest in studying the plasticity of ice for both glaciology and materials science studies.
2. Creep and Plasticity of the Single Crystal
2.1. Slip patterns and intermittent flow
Optical observations of basal slip lines by Reference NakayaNakaya (1958) have been widely used to show that basal slip dominates the ice plastic activity. Basal slip takes place through the motion of basal dislocations with the a/3(1120) Burgers vector. Basal dislocations gliding on basal planes are found to be far more numerous than those propagating on non-basal planes (Reference Petrenko and WhitworthPetrenko and Whitworth, 1999).
The creep response reveals a two-stage behavior with a transient stage during which strain rate increases with time due to dislocation multiplication (Reference Jones and GlenJones and Glen, 1969). From Reference Higashi, Koinuma and MaeHigashi and others (1965), stationary creep is observed for a strain of -0.2. During this second stage, strain rate is related to stress by a power law with a stress exponent of -2 (Fig. 1).

Fig. 1. Creep data for single and isotropic polycrystals at –108C (from Reference Duval, Ashby and AndermanDuval and others, 1983). Arrows for non-basal slip indicate that strain rate (or axial stress) should be lower (or higher).
Plastic flow on microscopic and mesoscopic scales proceeds in a heterogeneous and intermittent manner. Long-range interaction of dislocations leads to localization and intermittency. Dislocations move cooperatively in groups of spatially correlated slip planes rather than individually (Reference ZaiserZaiser, 2006). The most common method for studying the spatial heterogeneity of slip and dislocation patterns is to analyze the surface of deformed samples. Figure 2 shows basal slip lines in a large deformed ice single crystal imbedded in an ice matrix of very small grains, as observed by optical methods.

Fig. 2. Photograph of a sample deformed in uniaxial compression after a deformation of 6.3 × 10–2. The arrow indicates the c-axis direction. The monocrystalline inclusion was embedded in an isotropic matrix of fine grains (from Mansuy, 2001).
X-ray diffraction appears to be well adapted for bulk observation since ice is transparent to X-rays. An example of the distribution of dislocations – those that accommodate the torsion strain – along the axis of an ice sample deformed in torsion is shown in Figure 3 (Reference Chevy, Fressengeas, Lebyodkin, Taupin, Bastie and DuvalChevy and others, 2010). The c-axis being parallel to the torsion axis, the distortion of prismatic planes associated with torsion is accommodated with basal screw dislocations. The diffracted intensity along the torsion axis is directly related to the density of screw dislocations that accommodate the torsion. The heterogeneous distribution of dislocations is clearly shown. The power spectrum of the dislocation distributions, calculated from the FFT of the signal, is characterized by a scaling law, P(f) = f –μ (Reference MontagnatMontagnat and others, 2006), over a length scale range larger than several millimeters. Such a property indicates scale invariance of the diffracted intensity, and hence of the dislocation density distribution along the torsion axis. The exponent of the power spectrum, p, is 0.95 for this sample. This scale invariance implies that the dislocation density distribution is spatially correlated on a large scale. This indicates longdistance interactions between dislocations (Reference Weiss and MarsanWeiss and Marsan, 2003). These observations question the pertinence of widely used concepts such as the distance between slip lines and slip bands. This collective motion of dislocations is not restricted to ice but is a general feature of crystal plasticity (Reference Zaiser, Seeger, Nabarro, Duesbery and HirthZaiser and Seeger, 2002).

Fig. 3. Dislocation density distribution along the torsion axis after a strain of 56% (from Chevy and others, 2010). Acta Materialia by American Institute of Mining, Metallurgical, and Petroleum Engineers. Reproduced with permission of Pergamon via Copyright Clearance Center.
The collective motion of dislocations is associated with intermittent strain bursts. Although the existence of intermittent plastic strain bursts has been known for many years, a statistical characterization was first performed by acoustic emission experiments in ice single crystals by Reference Weiss and GrassoWeiss and Grasso (1997). It was shown that the size distribution of energy bursts follows a power law over several decades (Fig. 4;Reference Miguel, Vespignani, Zapperi, Weiss and GrassoMiguel and others, 2001). The individual motion of dislocations, as analyzed from X-ray topography measurements on thin samples with low dislocation density (Reference Petrenko and WhitworthPetrenko and Whitworth, 1999), could not represent the real situation for the deformation of the ice crystal. The dislocation velocity during avalanches is much higher than that of isolated dislocations (Reference MendelsonMendelson, 1963). Unfortunately, direct measurements during deformation are not possible. This power-law distribution of dislocation avalanches and the spatial heterogeneity of slip are both related to long- range dislocation interactions. These measurements of acoustic emissions on ice crystals are frequently used by the material science community when discussing the scale- free intermittent flow in crystals (Reference Dimiduk, Woodward, Le Sar and UchicDimiduk and others, 2006; Reference ZaiserZaiser, 2006).

Fig. 4. Distribution of acoustic energy bursts recorded in ice single crystals under creep tests at _108C. Inset is a typical recorded acoustic signal (from Miguel and others, 2001). Nature by Nature Publishing Group. Reproduced with permission of Nature Publishing Group via Copyright Clearance Center.
2.2. Rate-controlling processes for basal slip
The continuous increase of strain rate during creep is related to the multiplication of mobile dislocations by climb or cross-slip. Multiplication of basal screw dislocations by double cross-slip was suggested by Reference MontagnatMontagnat and others (2006) to explain the deformation of ice single crystals deformed in torsion. The dissociation of basal screw dislocations into widely extended partial dislocations should make the cross-slip process difficult (Reference Petrenko and WhitworthPetrenko and Whitworth, 1999). These dislocations must first constrict over a short distance to allow this process to begin. From Reference DuesberyDuesbery (1998), cross-slip is possible at all partial separations, provided that the stress is sufficiently large. In summary, the plasticity of single crystals of ice is governed by short- and long-range interactions between dislocations and not by lattice resistance. Multiplication of dislocations can be induced by both dislocation climb and cross-slip.
3. Creep and Plasticity of the Ice Polycrystal
Knowledge of the physical processes that occur during viscous deformation of freshwater polycrystalline ice is required to establish constitutive laws between the macroscopic variables of strain rate, strain, stress and temperature. There are strong arguments for considering basal slip as the main deformation process in the large range of equivalent stresses involved in glaciers and polar ice sheets. However, basal slip alone cannot accommodate the deformation. Other deformation modes must be invoked such as slip on non-basal planes, climb and cross-slip of basal dislocations. The large difference in behavior between the polycrystal and single crystals oriented for basal slip (Fig. 1) suggests that strain rate in polycrystals is not controlled by basal slip. On first loading, the stress state is uniform. As creep relaxes the shear stress on the basal plane, load is transferred to the harder non-basal systems. An increasingly non-uniform internal stress field develops. These internal stresses are long-range and oppose further deformation, i.e. they give directional or kinematic hardening. Long-range dislocation interactions are thus essential to explain the plastic flow of polycrystals (Reference Duval, Ashby and AndermanDuval and others, 1983).
Reviews of the creep behavior of polycrystalline ice are provided by Reference Weertman, Whalley, Jones and GoldWeertman (1973, Reference Weertman1983), Reference Duval, Ashby and AndermanDuval and others (1983), Reference Budd and JackaBudd and Jacka (1989), Reference Schulson and DuvalSchulson and Duval (2009) and Reference Cuffey and PatersonCuffey and Paterson (2010).
3.1. Long-range internal stresses and transient creep
Andrade’s law in t 1/3 for primary creep appears to be observed in many crystalline materials, in polymers and recently in ordinary paper (Reference Rosti, Koivisto, Laurson and AlavaRosti and others, 2010), leading to the conclusion that this should be explained from general principles, independently of materials properties.
Following the first theoretical explanation of Reference OrowanOrowan (1946) and Reference MottMott (1953), Andrade’s law should derive from a non-equilibrium phase transition with long-range interactions. For ice, owing to long-range dislocation interactions, the unlocking of a dislocation from an obstacle requires the escape by climb or cross-slip of a number of dislocations (Reference Louchet and DuvalLouchet and Duval, 2009). With this concept of load shedding and mechanical cascades, the transient creep can be analyzed in terms of criticality (Reference Miguel, Vespignani, Zaiser and ZapperiMiguel and others, 2002; Reference ZaiserZaiser, 2006). Dislocation motion during transient creep also appears to be characterized by avalanches (Reference Richeton, Weiss and LouchetRicheton and others, 2005), leading to the formation of slip lines and slip bands. However, in polycrystals, grain size sets the size of the largest avalanches; grain boundaries are obstacles to their propagation (Reference Richeton, Weiss and LouchetRicheton and others, 2005a).
Based on creep data of Reference JackaJacka (1984) obtained over a range of temperature and stress, a single master curve was obtained for polycrystalline ice (Fig. 5). The strain rate decreases by a factor of >100 during primary creep. The hardening is essentially kinematic or directional; it is responsible for the relatively large deformation recovered after unloading (Reference DuvalDuval, 1978) that also occurs through dislocation avalanches (Reference Richeton, Weiss and LouchetRicheton and others, 2005). Transient creep in ice was reproduced using an elasto/visco-plastic model and by introducing the progressive hardening of hard slip systems (Reference Castelnau, Duval, Montagnat and BrennerCastelnau and others, 2008).
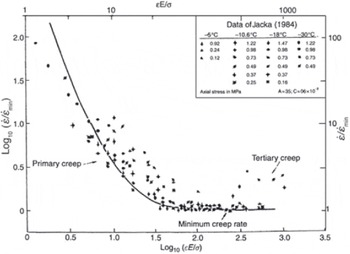
Fig. 5. Strain rate plotted against strain using reduced variables for isotropic ice (from Ashby and Duval, 1985). Cold Regions Science and Technology by Elsevier BV. Reproduced with permission of Elsevier BV via Copyright Clearance Center
The development of intragranular strain heterogeneities during transient creep was analyzed on two-dimensional (2-D) columnar ice using a digital image correlation technique (Grennerat and others, in press). Preliminary results indicate that local strain can be up to six times the average strain (~1%) during transient creep. Deformation bands stretching out over several grains are oriented at ~45° from the compression axis, and the level of local deformation is not correlated with grain orientation.
3.2. Long-range internal stresses and dynamic recrystallization
During deformation at relatively high temperature, recrystallization may take place. Dynamic recrystallization can occur by several mechanisms and can be continuous or discontinuous (Reference Guillope and PoirierGuillope and Poirier, 1979). During continuous recrystallization, sub-boundaries form as deformation proceeds, and high-angle boundaries may develop from the progressive misorientation of sub-boundaries. In this recrystallization regime, grain boundaries migrate in the same low-velocity regime as that associated with grain growth (Reference Duval, Ashby and AndermanDuval and others, 1983;Reference PoirierPoirier, 1985). Continuous dynamic recrystallization occurs extensively in polar ice sheets (Reference AlleyAlley, 1992;Reference Thorsteinsson, Kipfstuhl and MillerThorsteinsson and others, 1997;Reference De La Chapelle, Castelnau, Lipenkov and Duvalde La Chapelle and others, 1998) and is commonly observed during the hot deformation of metal alloys (Reference Humphreys and HatherlyHumphreys and Hatherly, 1996). This recrystallization mechanism leads to textures similar to deformation textures.
Discontinuous recrystallization results from the rapid migration of grain boundaries between dislocation-free nuclei and deformed grains (Reference PoirierPoirier, 1985). The grain boundary migration rate must be high in relation to the rate of accumulation of dislocations within the nucleus (Reference Roberts and AhlblomRoberts and Ahlblom, 1978). In ice, the grain boundary migration rate is typically 100 times larger than during continuous recrystallization (Reference Duval and CastelnauDuval and Castelnau, 1995). Discontinuous recrystallization gives coarse and interlocking grains, and recrystallized grains are well oriented for the easy basal slip (Reference Kamb, Heard, Borg, Carter and RaleighKamb, 1972;Reference DuvalDuval, 1981;Reference JackaJacka and Maccagnan, 1984). In the laboratory, such recrystallization textures form fora strain of <10% (Reference JackaJacka and Maccagnan, 1984). Recrystallization textures are stress-controlled and thus do not reflect the deformation history (Reference DuvalDuval, 1981; Reference AlleyAlley, 1992). This recrystallization process istheone that occurs in temperate glaciers and in ice sheets where temperature and stored energy are high enough. It corresponds to tertiary creep.
Nucleation of recrystallization
Recrystallization always proceeds from a deformed microstructure by the formation of nuclei and their growth. The driving force is the decrease of the stored energy within the embryo, but the formation of nuclei leads to additional interface energy. The total change in free energy, Ag, associated with the formation of a nucleus is given by
where r is the radius of the embryo, γ gb is the grain boundary energy and Δg v is generally considered as the stored energy within the embryo.
The critical radius corresponding to the maximum of the free energy is given by
For ice with a dislocation density of 1012m-2, a relatively high value for polar ice sheets (Reference Montagnat and DuvalMontagnat and Duval, 2000), Δg v = 300Jm-3 and r* = 0.4mm; the free energy at the maximum is Δg* = 4.8 × 10-8J. In metals, the stored energy is much higher, giving a critical radius generally less than 10mm (Reference GottsteinGottstein, 2004).
Calculations based on nucleation theory involving thermal fluctuations (Reference ChristianChristian, 1965) indicate that the radius of the critical nucleus is so large that the rate of nucleation will be negligible. It is therefore accepted that the nucleation step is associated with instability of the dislocation microstructure within original grains (Reference Humphreys and HatherlyHumphreys and Hatherly, 1996;Reference Brechet and MartinBrechet and Martin, 2006). Recrystallization at preexisting high-angle boundaries is known to be a very important process since it implies low strain and high temperature. Strain-induced grain boundary migration involves the bulging of part of the grain boundary due to different stored energies on opposite sides of the boundary (Reference Humphreys and HatherlyHumphreys and Hatherly, 1996).
Grain nucleation during dynamic recrystallization in ice was recently analyzed by considering the interaction of a nucleating grain with the long-range internal stress field that develops during primary creep (Duval and others, arxiv.org/pdf/1007.4878). We suggest that long-range internal stresses may significantly reduce the size of the critical nucleus because grain nucleation relaxes this internal stress field over a distance much higher than the embryo. As a consequence, the free energy associated with grain nucleation includes an additional energy corresponding to the reduction of dislocation density outside the embryo. Taking into account the rearrangement of dislocation pile-ups following the absorption of leading dislocations by a dislocation-free embryo allows the critical radius to be very small and the energy of the embryo to decrease continuously with increasing size. Both situations with and without a critical stored energy to initiate grain nucleation are shown in Figure 6. The main assumption in this theoretical analysis is that much of the energy needed to form a new grain comes from the relaxation of long-range internal stresses associated with the nucleation of a new grain. The low critical strain, εc (of ~1%), required to initiate dynamic migration recrystallization in ice could be explained by these processes and therefore be associated with large strain and stress heterogeneities in the polycrystal.

Fig. 6. Schematic free energy of formation of a nucleus as a function of the nucleus size: (top) with ![]() and (bottom) by taking into account the effect of long-range internal stresses.
and (bottom) by taking into account the effect of long-range internal stresses.
3.3. Dynamic discontinuous recrystallization fabrics in glaciers and ice sheets
Dynamic discontinuous recrystallization in ice induces fabrics that are very different from deformation fabrics. As observed in temperate glaciers (Reference RigsbyRigsby, 1951) and in the laboratory (Reference SteinemannSteinemann, 1958;Reference Kamb, Heard, Borg, Carter and RaleighKamb, 1972;Reference DuvalDuval, 1981; Reference JackaJacka and Maccagnan, 1984), most crystals are well oriented for basal slip. In uniaxial compression, a girdle fabric develops around the compression axis, with c-axes at ~30° from the compression axis (Reference JackaJacka and Maccagnan, 1984), whereas slip induces a fabric with most of the c-axes around the compression direction. In polar ice sheets, recrystallization fabrics may not contain orientations present in deformation textures. Figure 7 shows the microstructure of ice from the Antarctic Talos Dome ice core at 1171 m depth and the orientation of c-axes. Most grains are oriented along the vertical direction, which can be assumed parallel to the in situ compression axis. The orientation of the few large grains, probably induced by discontinuous recrystallization, appears to be very far from the orientation of the other grains, due to the rotation of the lattice by basal slip.

Fig. 7. Fabric of an ice sample from the Talos Dome ice core; Rxx shows the correspondence between the ice texture and fabric for two grains. Talos Dome is on the edge of the East Antarctic plateau (72°47′ S, 159°04′ E; 2318ma.s.l.); a 1620m ice core was recovered in 2007 (Urbini and others, 2008).
Discontinuous recrystallization therefore seems to be associated with the development of grains with orientations outside the spread of orientations corresponding to deformation fabrics. This situation, for which continuous and discontinuous recrystallization coexist at the same depth, is in agreement with the instability in the grain boundary migration rate as described by Reference Guillope and PoirierGuillope and Poirier (1979). Grain nucleation by subgrain rotation and grain nucleation by local strain-induced grain boundary migration are well- accepted mechanisms for continuous recrystallization. However, they cannot be at the origin of fabrics that form during discontinuous recrystallization since the orientation of new grains should reflect the orientation of the parent grains. Grain nucleation in the presence of large orientation gradients could give grains with orientations different from those of parents, but they should inherit their orientation from them. The stress-controlled orientation pattern associated with discontinuous dynamic recrystallization in ice (Reference DuvalDuval, 1981) clearly rules out a direct relation between the orientation of grains before and after dynamic discontinuous recrystallization.
The role of internal stresses in the nucleation of grains, as assumed above, could be important in the development of these stress-controlled textures. The long-range internal stress field is modified and relieved by the continuous nucleation and growth of grains. On the other hand, as discontinuous recrystallization produces grains well oriented for basal slip, the density of excess dislocations during recrystallization, i.e. those that accommodate long-range internal stresses, should be lower than that expected before recrystallization starts. Recrystallization textures could therefore be seen as those that minimize the long-range internal stress field.
4. Modeling Approaches
Efforts to simulate the mechanical behavior of ice polycrystals aim at modeling ice flow and fabric evolution along polar ice cores. More recently, ice has been recognized as a ‘model material’ for validating micro-macro full-field modeling approaches for extreme visco-plastic anisotropy.
Reference Castelnau, Canova, Lebensohn and DuvalCastelnau and others (1997) first applied the visco-plastic self-consistent (VPSC) scheme to ice polycrystals to characterize the relation between the texture of the material and the instantaneous anisotropic mechanical behavior. The VPSC approach, which has been widely used for ice viscoplastic behavior modeling, is a micro-macro approach which seeks to derive, according to active deformation mechanisms, an interaction equation that links microscopic state (stress and strain rate at the grain scale) with the macroscopic state (the polycrystal scale) (Reference Lebensohn and ToméLebensohn and Tomé, 1993). The grain inside the polycrystal is represented by an inclusion in a homogeneous equivalent medium, whose mechanical behavior is that of the polycrystal. This is currently referred to as a ‘one-site’ scheme.
Such a homogenization method is based on several approximations. In order to deal with the nonlinearity of the relation between the strain rate and stress (with a stress exponent of 3 for ice), the VPSC approach is based on linearization schemes bounded by the static estimate (uniform stress in all grains) and the Taylor estimate (uniform strain rate). The tangent approach, used by Reference Castelnau, Thorsteinsson, Kipfstuhl, Duval and CanovaCastelnau and others (1996b, Reference Castelnau, Canova, Lebensohn and Duval1997) to represent the mechanical behavior of anisotropic ice or to model the fabric evolution along ice core, was recently shown to be not well adapted for representing the behavior of highly anisotropic materials (Reference Lebensohn, Liu and Ponte CastanedaLebensohn and others, 2004). Since then, a second-order approach, which considers the second moment of stress and strain rate in order to obtain the local linearized behavior, was shown to better represent the mechanical behavior of ice (Reference Liu and Ponte CastanedaLiu and Ponte Castaneda, 2004).
The visco-plastic modeling requires knowledge of the constitutive relation at the single-crystal scale. In particular, the grain scale deformation comes from slip on several slip systems whose local activity depends on the Schmidt factor, a critical resolved shear stress (CRSS) and a possible hardening law for every slip system. In the case of ice, very little evidence exists of slip on non-basal systems. Nevertheless, four systems are required in the self-consistent scheme to enable all possible deformations (Reference HutchinsonHutchinson, 1976). Prismatic and pyramidal slip systems are then used and their relative activity is regulated via the CRSS and its evolution with a parameterized hardening law if necessary. The values, which are model-dependent, can be adjusted with mechanical test results using inverse methods (Reference Castelnau, Canova, Lebensohn and DuvalCastelnau and others, 1997). Doing so, good estimates of the behavior of isotropic or strongly textured ice could be reproduced.
The tangent approach was applied by Reference Castelnau, Thorsteinsson, Kipfstuhl, Duval and CanovaCastelnau and others (1996a) to model the fabric evolution along the Greenland Icecore Project (GRIP) ice core, the ‘dome-like’ configuration of which allowed the assumption of deformation under compression at a constant strain rate. The model provided predictions in good agreement with measurements in the upper 650 m of the core, but predicted fabrics below 650 m were too concentrated. Dynamic continuous recrystallization mechanisms, which were not considered in the modeling approach, were supposed to explain most of the discrepancy, but a nearest-neighbor interaction scheme associated with a static estimate gave a better result (Reference ThorsteinssonThorsteinsson, 2002). Stress redistribution within the polycrystal could also be indirectly taken into account by integrating the intragranular stress and strain- rate fields in the VPSC linearization procedure as made possible by the second-order approach (Reference Liu and Ponte CastanedaLiu and Ponte Castaneda, 2004). This approach predicts a quasi-persistent accommodation of deformation by basal slip, even when the c-axes become strongly aligned with the compression axis (Reference Lebensohn, Tomé and Ponte CastanedaLebensohn and others, 2007). Furthermore, a very good match with measured fabric evolution along the Antarctic EPICA Dome C core is obtained by applying a uniaxial compression at a constant rate as long as migration recrystallization does not occur (Fig. 8).

Fig. 8. VPSC second-order prediction of fabric evolution along the EPICA Dome C ice core (expressed via the eigenvalues of orientation tensor a (2) (from Durand and others, 2006), compared with measurements (Durand and others, 2009). Solid curves represent an anisotropic initial fabric, the dashed curve an isotropic one. Symbols plot the measured a (2) eigenvalues
More recently, the full-field formulation based on FFTs from Reference LebensohnLebensohn (2001) was used to predict the micromechanical fields that develop in 2-D columnar ice polycrystals deforming in compression (Reference Lebensohn, Montagnat, Mansuy, Duval, Meyssonnier and PhilipLebensohn and others, 2009). This micro-macro approach allows solution of the governing mechanical behavior on every point of a Fourier grid which discretizes the polycrystal represented as a representative volume element (RVE). The RVE polycrystal is then periodized in order to solve the constitutive equations in the Fourier space. Doing so, mechanical fields can be obtained at an intragranular scale very similarly to finite-element approaches but at a much lower computational cost. As shown in Figure 9, the model predicts very well the location of strain concentration (strain-rate field maps), in comparison with measured strain field using digital image correlation techniques on ‘2-D’ columnar ice samples deformed by compression creep up to 1% strain (Grennerat and others in press).

Fig. 9. Comparison between (a) measured equivalent strain field in columnar ice and (b) simulated strain-rate field using the full-field viscoplastic FFT approach. In both cases, values are normalized by the average.
5. Conclusions
This work attempts to show the essential role of long-range dislocation interactions in the plastic behavior of ice single crystals and polycrystals, and stresses the role of ice as a model material to analyze this important topic from a more generic point of view.
The intermittent and scale-free nature of plastic flow in materials was revealed by acoustic emission studies in ice crystals. Strain bursts produced by dislocation avalanches are triggered by long-range interaction stresses between dislocations and should contribute to the essential part of the macroscopic strain in single crystals. There is a direct connection between avalanches and the formation of dislocation patterns in the form of slip lines or slip bands, which exhibit long-range spatial correlations. Dislocation multiplication by cross-slip is suggested in spite of the expected dissociation of basal dislocations.
Primary creep in polycrystals is analyzed by considering directional hardening induced by slip incompatibility between grains and softening by climb or cross-slip of basal dislocations. Both processes involve a large number of interacting dislocations. Based on experimental measurements and simulations of the mechanical behavior, it is shown that very large stress and strain intragranular heterogeneities build up with deformation. They are responsible for initiating dynamic recrystallization for a relatively low critical strain. Grain nucleation during discontinuous recrystallization is analyzed by considering the relaxation of long-range internal stresses, occurring as soon as an embryo forms. With this additional driving force, a negligible critical free energy for the formation of a nucleus could be obtained. This assumption, if confirmed, gives an original view of grain nucleation during dynamic recrystallization in ice, but also in other materials. In this context, stress-controlled fabrics in glaciers and polar ice sheets can be understood.
Ice is thus a marvelous material which warrants many years of study by ice glaciologists and geophysicists. It is now also considered a model material for understanding deformation processes in metals, and for polycrystal modelling.
Acknowledgements
We are grateful to the International Glaciological Society for inviting this contribution, and to G.K.C. Clarke and a reviewer for their encouragement. This work was supported by CNRS (Institut des Sciences de l’Ingenierie et des Systemes (INSIS)) and the Universite Joseph Fourier, Grenoble, France. We thank PhD students a part of whose work is described in this paper. We gratefully acknowledge C. de Loustal and P. Fabry for the preparation of figures.











