1. Introduction
Glacier-wide net mass balance is the net gain or loss of mass of an entire glacier during a given balance year; summing the net balance over a series of years results in a cumulative balance (Reference PatersonPaterson, 1994). Temporal cumulative mass-balance trends in a region indicate climate variability (Reference Oerlemans and FortuinOerlemans and Fortuin, 1992; Reference Hodge, Trabant, Krimmel, Heinrichs, March and JosbergerHodge and others, 1998; Reference Dyurgerov and MeierDyurgerov and Meier, 2000) and these trends, if sustained, can have a large effect on sea level (Reference HoughtonHoughton and others, 2001; Reference Arendt, Echelmeyer, Harrison, Lingle and ValentineArendt and others, 2002). However, only 33 glaciers worldwide have a balance record greater than 40 years (Reference Dyurgerov and MeierDyurgerov and Meier, 1997), so one or two glaciers are often used to represent hundreds of glaciers in a region (e.g. Reference MeierMeier, 1984). Although region-wide extrapolations may cause inaccuracies, in some areas the cumulative mass balance of a single glacier can represent the mass balance of a region (e.g. Reference Rabus and EchelmeyerRabus and Echelmeyer, 1998). A more fundamental problem is the accuracy of the limited number of mass-balance records used for extrapolation.
The conventional method to measure mass balance, which we refer to as the glaciological method, relies on balance measurements made at a discrete number of points. These measurements are then extrapolated over the glacier, usually on the basis of the area-altitude distribution (AAD) (Reference Østrem and BrugmanØstrem and Brugman, 1991). When done correctly, the glaciological method also includes glacier-wide estimates of internal accumulation and internal ablation, which if not accounted for can lead to annually small but cumulatively significant systematic errors.
The glaciological method is the only mass-balance method that records point balances, which are directly related to climate without any bias by glacier geometry. It is also the only method used to measure seasonal and annual balances over the long term. However, the accumulation of errors can be problematic in the glaciological method. We are concerned primarily with systematic errors because they increase linearly with the number of years (N) in the record, whereas random errors increase as ![]() It is thus important to determine whether the errors in the glaciological method are predominantly random, or whether a large systematic component is present in the given balance record.
It is thus important to determine whether the errors in the glaciological method are predominantly random, or whether a large systematic component is present in the given balance record.
An independent method used to check and possibly calibrate the cumulative glaciological balance is the geodetic method (Reference Fountain, Krimmel and TrabantFountain and others, 1997). In this method, the surface elevation of the glacier is surveyed at intervals of a few years to a few decades. Differencing these elevations and applying adjustments for density and other factors gives the glacier-wide cumulative balance over the time interval between maps. The geodetic method accounts for all spatial variability in balance, assuming that the elevations are accurate everywhere, and references a stable geographic datum. However, point balances are not calculated since surface elevation changes include flow in addition to balance.
The glaciological and geodetic methods measure the same quantity, the glacier-wide balance, but the results differ because of different errors inherent in each method. Errors in the glaciological balance result from measurement poles sinking into the snowpack, incorrectly defined previous seasonal surfaces and overlooked internal accumulation and ablation (Reference HaakensenHaakensen, 1986; Reference Conway, Rasmussen and MarshallConway and others, 1999; Reference KrimmelKrimmel, 1999). These errors are summed over the glacier and combine with cross-glacier variations in balance from surface irregularities, avalanches, wind deposits or scours and topographic shading (Reference Fountain and VecchiaFountain and Vecchia, 1999; Reference KrimmelKrimmel, 1999). Such errors can accumulate systematically over time. In some instances, these errors have caused the measurement of glaciological balance to have the opposite sign to the geodetic balance (Reference Conway, Rasmussen and MarshallConway and others, 1999).
Errors associated with the geodetic method are primarily the result of poor photogrammetric contrast areas and poor digital elevation model (DEM) registration, which can cause the balance to vary by several times the realistic value (Reference AndreassenAndreassen, 1999; Reference Østrem and HaakensenØstrem and Haakensen, 1999). Poor contrast prohibits stereo perception and therefore accurate elevation extraction. This can be a problem in snow-covered areas, but crevassed zones and ice generally provide good contrast. Moreover, the geodetic method typically assumes the density of material lost or gained on the glacier is equal to the density of ice, so loss or gain of firn or any change in the depth-density relation within the firn can affect the conversion of volume to mass. This error is not necessarily independent of time, given a steadily advancing or retreating glacier. However, these errors are much less time-dependent than possible systematic errors in the glaciological method, making the geodetic balance more accurate than the glaciological balance over time-scales longer than a few years. The geodetic method can thus be used to calibrate the glaciological cumulative balance (Reference Elsberg, Harrison, Echelmeyer and KrimmelElsberg and others, 2001).
The mass-balance record on Gulkana Glacier, Alaska, is especially important because it is one of the few long-term mass-balance records in the United States (1966-2003). It is one of three index glaciers chosen for long-term balance monitoring by the U.S. Geological Survey (USGS) and is the only one of these in a continental climate zone (Reference MarchMarch, 1998). It is often used for studies in glacier-climate interaction and sea-level change (Reference Letréguilly and ReynaudLetréguilly and Reynaud, 1989; Reference Dyurgerov and MeierDyurgerov and Meier, 1997). However, the present mass-balance record has not been checked against an independent method. In this paper, we determine the geodetic balance over two intervals for comparison with, and possible calibration of, the glaciological record.
Gulkana Glacier is located in the eastern Alaska Range (63°16’N, 145°25’W; Fig. 1). It has three accumulation cirques, facing approximately southeast, south and west; the maximum elevation is 2450 m in the southeast-facing cirque known as the Minya basin. Ice from the three accumulation areas merges below the average equilibrium-line altitude (ELA) of 1780 m and flows south to the terminus at 1200 ma.s.l. (Reference MarchMarch, 2000). The terminus has retreated 3 km since its Little Ice Age maximum around 1900 (Pewe and Mayo, 1983) and about 300 m since 1974. Glacier area has decreased from 18.4 km2 in 1974 to 17.1km2 in 1999. The average balance gradient with elevation between the highest and lowest index sites varies over time from 0.006 a to 0.010 a-1. Air temperature and precipitation have been measured since 1967 at a weather station located at 1480 m on a moraine east of the lower glacier; the record is 93% complete (Reference Kennedy, Mayo, Trabant and MarchKennedy and others, 1997).

Fig. 1. Location map. Gulkana Glacier is located on the southern side of the eastern Alaska Range. FBKS and ANC refer to the cities of Fairbanks and Anchorage, respectively.
Surface motion and mass balance have been measured by the USGS at three index sites on the glacier (labelled A, B and D as shown in Figure 2) since the mid-1970s (Reference MarchMarch, 2000). Three laser altimetry elevation profiles were flown in 1993, 1995 and 2000 (Reference EchelmeyerEchelmeyer and others, 1996; Reference Arendt, Echelmeyer, Harrison, Lingle and ValentineArendt and others, 2002), and the glacier elevation profile was surveyed optically in 1993.

Fig. 2. Index site, weather station and control point locations. The area with poor contrast in the 1999 photographs and missing from the 1974 photographs is hatched by diagonal lines.
2. Geodetic Balance
2.1. DEM creation
Geodetic balances for Gulkana Glacier were calculated using aerial photography from 1974, 1993 and 1999 (Table 1). Three DEMs of Gulkana Glacier were generated from the aerial photographs using a digital photogram- metry system (PCI Geomatics APEX). The digital process is similar to analytical photogrammetry except that the photographs are scanned to create a digital image, the extraction of elevations is semi-automated and a threedimensional viewing system is used to edit the DEMs. Scan resolution limits horizontal accuracy to 1-2 times the ground pixel size (the ground dimension represented by one pixel), and vertical accuracy to 0.5-3 times the ground pixel size, as shown inTable 1 (PCI Geomatics, 2000).
Table 1. Data collected on Gulkana Glacier. These data were used to prepare DEMs and assess DEM accuracy

Two types of control are used to orient images: control points, which orient the images to absolute ground coordinates, and tie points, which align the images with each other. In 1992, ten control points were surveyed to about ± 0.1 m using the global positioning system (GPS) (Fig. 2); these were marked on the ground with 10 m long intersecting white panels that were easily identifiable on the images acquired the following year. Images from 1974 and 1999 lacked these or any other marked control points; they were oriented using obvious features such as rock outcrops and mountain peaks. When these features are selected in multiple images, they become tie points which control the 1974 and 1999 images to the ground coordinates measured in the 1993 images. A total of 170 tie points on bedrock were used as coincident image points for this relative control. No accuracy is lost using the tie points instead of control points in the 1974 and 1999 images.
After the images were controlled, co-registered DEMs were extracted from the images using an image correlation algorithm. We found 5 m grid spacing to be optimal for image correlation. To facilitate manual editing, which was needed on about 10% of the glacier, the grids were re-sampled glacier-wide to a 25 m spacing. Reference AndreassenAndreassen (1999) has demonstrated that this is a suitable grid spacing for geodetic balance calculation on a glacier one-third the size of Gulkana Glacier. Manual editing was needed in areas of low contrast, such as the upper Minya basin, where bright snowfields displayed few features to be correlated. Grids were not extracted from the 1999 Minya basin because of poor contrast; instead, a triangulated irregular network (TIN) was used. Unlike the grid method, in which the software picks a point at every grid node regardless of accuracy, the TIN method effectively extracts only points inside a certain confidence interval. This method eliminates the need for manually editing thousands of inaccurate points, although some accuracy is lost because the point density may be reduced by as much as a factor of ten in poor-contrast areas.
2.2. Adjustments
Before the DEMs can be differenced, each DEM needs to be adjusted for ablation, emergence and density so the geodetic balance can be compared directly to the glaciological balances and independent surveys. Ablation and emergence adjustments were applied because the date of photography did not coincide with the end of the ablation season, which is when the glaciological balance was measured (Table 2), or with the date of the laser and optical profiles. Density adjustments convert snow or ice volume to water equivalent volume change.
Table 2. Seasonal adjustment interval. The duration of seasonal adjustment is shown with the glacier-wide ablation adjustment
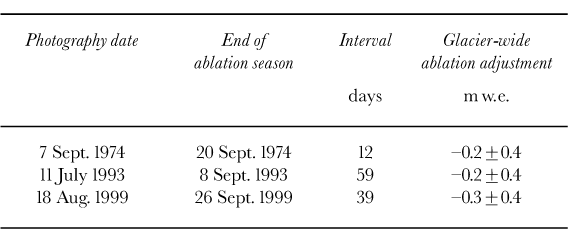
Ablation and emergence adjustments depend on the glaciological measurements, removing the complete independence of the two methods. They are also subject to the same limitations as the glaciological method, namely the small spatial distribution of data. The lowest index site is near the terminus, and only a small percentage of the glacier area and elevation is extrapolated below this point. However, roughly 50% of the glacier is above the highest site.
Instead of merely extrapolating and interpolating ablation data from the measurement sites, we used a simple degree-day model following Reference ReehReeh (1991) to calculate the total ablation adjustment. Measured summer precipitation and temperature from the 1480 m weather station for each year were input into a one-dimensional model. The model was then tuned by varying temperature lapse rates and snow and ice degree-day factors to force the modelled summer balance to match the summer balance measured at each index site. Finally, the ablation in meters of water equivalent from the date of photography to the end of the balance year was calculated as a function of elevation and weather data using the tuned parameters. During each of the three years, an abnormally high ELA drove the snowline above the highest pole. This accounts for the kink in the ablation adjustment at the snow/ice transition above the highest site (Fig. 3). The 1993 adjustments are relatively large, especially at low elevations, because of the long time interval and the fact that this period extended over the most intensive part of the ablation season. Though large, the 1993 adjustment is well controlled by index-site measurements near the time of the photography. Internal ablation and accumulation are assumed to be negligible over the intervals.

Fig. 3. Ablation adjustments. Adjustments were tuned to match measured summer ablation at index sites. Elevations of index sites are represented by vertical dotted lines. The curves represent the balance with elevation over the adjustment interval (Table 2).The total estimated error for each adjustment interval is ±0.4 m w.e.
Each DEM was also corrected for total emergence from the photo date to the end of the ablation season over the interval shown in Table 2. Any change in the surface elevation of the glacier at a point not caused by ablation is caused by the emergence velocity, that is, the component of velocity perpendicular to the surface (Reference PatersonPaterson, 1994). The total emergence is defined as the cumulative surface elevation change at a specific point. Emergence does not affect glacier-wide balance because it is merely a redistribution of mass along the entire glacier. Nevertheless, the DEMs were corrected for emergence velocity for two reasons: (1) to compare more accurately the individual DEM points with optical and laser profiles (see section 2.4), and (2) to represent more accurately the thinning in specific areas at the end of the ablation season. Emergence was measured seasonally at the three index sites. We assumed the emergence rate was constant over each measurement interval, and calculated the total emergence at each index site for each seasonal adjustment interval. A curve was fit through these calculated values for each interval. The curve was adjusted to the shape of the extended mass-balance curve (see section 3) since the shape of the emergence and balance curves should be complementary. Flow was not measured in 1974, so the average summer emergence from 16 years’data at each index site was used. While this is less accurate than measured values, the adjustment interval was only 12 days, with a maximum adjustment of 0.10 m on the lower glacier. The shape of the 1993 curve differs from the others because measured emergence at the mid-glacier site (B) was greater than that at the index site low in the ablation area (Fig. 4). The 1993 emergence rates have been checked against the original measured data and, other than the shape of the curve, there is nothing to suggest the measurements are inaccurate.

Fig. 4. Total emergence as a function of elevation. Emergence was measured over the adjustment intervals at the index sites, represented by vertical dotted lines. The estimated error at each elevation is ±0.2 m, but when integrated over the glacier the emergence sums to 0±0.03 m.
Thickness changes of ice or snow were converted to water equivalent on the basis of density of the material lost or gained. We assumed Sorge’s law, which states that density structure remains constant in an unchanging climate (Reference BaderBader, 1954). This allowed us to assume that the change in volume is related directly to water equivalent volume by the density of ice (900 kg m-3; Reference PatersonPaterson, 1994).
2.3. Surface elevation change
Surface elevation change was calculated by subtracting the DEMs, identifying and checking for possible errors and re-subtracting the DEMs. Where large surface change variations (defined as deviations larger than 5 m from those in adjacent areas) are present after DEM subtraction, these points were re-measured from the aerial photographs. Typically, large surface change variations were a result of an incorrect elevation, but large drifts and crevasses also caused deviations in the surface change. In some locations the elevation simply could not be extracted because of poor contrast. These locations were given a ‘no data’ value and then skipped in the re-subtraction. The surface elevation change was interpolated through missing points after re-subtraction since the surface change should be smoother and interpolate more accurately than the glacier surface.
The upper 2.7 km2 of the Minya basin did not contain registered grids to subtract because the 1974 photography did not cover this area and the 1999 photographs had low contrast (Fig. 2). The surface elevation in the Minya basin was assumed not to have changed from 1974 to 1993 because (1) high areas of the glacier for which coverage existed showed no change over the interval, and (2) surface change of the lower Minya basin tended to zero at the edge of coverage. However, the surface elevation did show change from 1993 to 1999. The 1999 TIN in the upper Minya basin was subtracted only from coincident 1993 gridpoints.
When all the adjustments were applied, the elevation changes shown in Figure 5 were obtained. The cumulative geodetic balance is the surface elevation change integrated over the glacier. The 1974-99 geodetic balance was the sum of the balances for the two intervals. The geodetic balance from 1974 to 1993 was -6.0 m w.e., and from 1993 to 1999 it was -5.8 m w.e. Addition of these two balances resulted in a strongly negative balance over the entire interval 1974-99 (Table 3).

Fig. 5. Surface elevation change, in meters of water equivalent. The maps are the two intervals 1974-93 (a) and 1993-99 (b). The estimated accuracy for the maps is ±1.0 m w.e.
Table 3. Cumulative geodetic and glaciological balances

2.4. Errors
Errors in the geodetic balance can result from seasonal adjustments, density adjustments and image control and quality. Emergence adjustments should not affect the glacier-wide balance. We verified that they did not affect the geodetic balance by integrating the total emergence over the glacier; the integration result for each year was <0.05 m. Seasonal balance adjustments are the largest source of error. The 1993 data had the longest adjustment duration, but the index-site poles were surveyed almost coincident with the time of photography, so the adjustment is better constrained. The 1974 and 1999 data are less well constrained, but are adjusted over a shorter interval. We estimate the error of these adjustments to be ± 0.4 m w.e.
The small shift in the ELA during the measurement period and the relatively small balance gradient make the assumption of Sorge’s law plausible for Gulkana Glacier. Data from snow pits show no temporal systematic change in density. Reference Elsberg, Harrison, Echelmeyer and KrimmelElsberg and others (2001) showed that using a constant density conversion of 900 kg m-3 will cause a 5.5% error in the geodetic balance if firn and ice are lost in the middle half of the glacier instead of ice, as might be expected on a retreating and thinning glacier. Gulkana Glacier has experienced much less change than the glacier on which Elsberg and others performed the sensitivity analysis (South Cascade Glacier, Washington, U.S.A), so any error associated with assuming Sorge’s law will be less than ± 0.3 m w.e.
The image control and quality were checked by independent surveys of the glacier in 1993 and 2000. Fifty-six points were surveyed on the glacier in 1993 to an accuracy of ±0.1 m (Table 1). These points were well distributed over the glacier, with one profile up each of the main branches and several transverse profiles. Each of the profiles was subjected to the same seasonal adjustments as were the DEMs. Comparison of DEM elevations with the optically surveyed points shows that the 1993 DEM is 0.8 ± 0.5 m too low (Table 4). No trend to the average offset with elevation is apparent, although the standard deviation is greater for points in the accumulation area.
Table 4. DEM accuracy. The standard deviation about the mean is greater over the bedrock than over the ice, and the relative error among DEMs is small

Airborne laser altimetry profiles flown in 1993 and 2000 measured surface elevations to an accuracy of about ± 0.3 m (Reference EchelmeyerEchelmeyer and others, 1996). Large seasonal corrections that enabled us to compare laser profiles with DEMs caused the uncertainty to increase in the comparison to ±1.0 m. These profiles cover the center line of the main branches in an almost continuous line down the glacier (Reference Sapiano, Harrison and EchelmeyerSapiano and others, 1998). The 1993 DEM was 0.6 ± 1.0 m lower than the adjusted 1993 laser profile, and the 1999 DEM was 0.2 ± 1.0 m lower than the adjusted 2000 laser profile. These laser profiles also show no spatial trends in the difference, which indicates that the DEMs are not sloping relative to the datum. The laser and optical profiles show the DEMs as a group to be about 0.5 m low relative to the datum.
The relative accuracies of the DEMs were checked by subtracting two DEMs over bedrock. The relative error of the DEMs is more important than their absolute error when calculating geodetic mass balance. The relative error indicates the accuracy of the geodetic balance, while the absolute error demonstrates DEM control to a datum. Several problems may make point measurements over bedrock less accurate than those over ice. (1) The photographs were scanned to optimize contrast over the ice and snow areas; this procedure made the bedrock dark (and often black) in many areas, even with the contrast and brightness optimized in each area when manually editing the DEMs. (2) Bedrock areas were not manually edited as carefully as the glacier areas. (3) Except for a few locations, the only snow-free areas near the upper glacier are nearly vertical, so large elevation errors may result from small horizontal registration errors. The increased standard deviation about the mean of the DEM over bedrock, compared with measurements over the glacier, illustrates these problems. In spite of the difficulties, the bedrock differencing gave encouraging results: relative error of the DEMs was within 0.3 m.
On the basis of these estimates and using standard propagation of error, we estimate the error in the geodetic balances to be ± 0.7 m w.e.
3. Glaciological Balance
The USGS has used the glaciological method to determine the net mass balance on Gulkana Glacier every year since 1966. In this method, the end of the balance year is defined as the date of the yearly glacier-wide minimum balance. An extended network of as many as 30 mass-balance stakes was maintained until the mid-1970s, when the network was reduced to three index sites (Fig. 2) and measurements were expanded to include ice motion and surface elevation at these sites (Reference MarchMarch, 2000). The long-term balance has been calculated using one consistent methodology and the data from these three index sites. The highest index site (D) is generally just above the ELA, but the ELA has been above site D three times. The seasonal balance is measured in an area 25-75 m around each pole in an effort to reduce errors from individual snow-depth soundings and small-scale surface irregularities (Reference Trabant and MarchTrabant and March, 1999).
To calculate the glacier-wide balance from index-site measurements, the glacier is divided into three elevation bins. Bin boundaries occur at elevations halfway between the elevations of sites A and B and sites B and D. Bin boundaries are updated each year for variations in index-site altitude, but not for changes in glacier area. The map area of each elevation bin is divided by the total area of the glacier to obtain an area weighting factor. This is equivalent to using an AAD. The weighting factor is multiplied by the balance at each site, and the results are summed to determine the glacier-wide surface balance including internal accumulation. Estimated internal ablation from geothermal heat, ice motion and water flowing through and under the glacier is added to the surface balance to obtain a glacier-wide net balance (Reference MarchMarch, 2000). The internal ablation from geothermal heat and ice motion does not change annually, but internal ablation from water flow is calculated from total runoff and varies by a factor of two from year to year.
All previously published balance measurements on Gulkana Glacier have been referenced to a fixed AAD, which does not yield the actual mass balance. For this comparison, we have established time-variable AADs by calculating the AAD from DEMs of 1974,1993 and 1999. AADs were interpolated for the intervening years. The cumulative glaciological balance shows the trend towards more negative balances in the 1990s (Table 3; Fig. 6).

Fig. 6. Glaciological balances: (a) net balance and (b) cumulative balance. The cumulative balance is bounded by random (dark gray) and possible systematic (light gray) errors of 0.2 m w.e. a-1.
The published error for the net glaciological balance on Gulkana Glacier is 0.20 m a-1 (Reference MarchMarch, 1998). This is found by propagating errors from measurements such as snow-pit densities, multiple snow-depth soundings, multiple angles when surveying and estimates of the representativeness of the sites.
4. Discussion
4.1. Glaciological method accuracy
The comparison between geodetic and cumulative glaciological balances is shown in Figure 7 and Table 3. The comparison is excellent; the geodetic balance is within the estimated error bars of the glaciological balance. This implies that the glaciological balance record on this glacier does not contain large systematic errors.

Fig. 7. Comparison of cumulative glaciological and geodetic mass balances. The geodetic balance is within the random error of the glaciological balance.
Several balance components included in the glaciological method appear insignificant in the net balances, but have a large cumulative effect over decades. For example, an approximately 0.05 m w.e. a-1 internal ablation is included in the net balance. Systematically ignoring this small factor would have decreased the cumulative glaciological balance by about 10%. Other techniques have been employed to avoid common pitfalls such as incorrectly determining the previous season’s summer surface. For example, poles driven into the snowpack can cause systematic under-estimation of the winter balance. This force can be so great that on Ålfotbreen, Norway, poles have been forced through plywood at their base by snow compaction (Reference Østrem and HaakensenØstrem and Haakensen, 1999). Sawdust or other artificial horizon placed on the summer surface allows unambiguous depth sounding by drilling or coring the following spring (Reference Trabant and MarchTrabant and March, 1999). In addition, single point measurements are not necessarily representative of the immediate area: deviations of 0.23 m w.e. in one year have been observed on three stakes <5 m apart (Reference Braithwaite and OlesenBraithwaite and Olesen, 1989). Errors from these small-scale variations are eliminated by sampling the balance in an area tens of meters around each index site in both the ablation and accumulation seasons (Reference Trabant and MarchTrabant and March, 1999).
Even with perfect point balances, three poles typically have not been found sufficient to determine accurately the mass balance on glaciers the size of Gulkana Glacier; a minimum of five to ten poles is recommended (Reference Østrem and BrugmanØstrem and Brugman, 1991; Reference Fountain, Krimmel and TrabantFountain and others, 1997). The method of extrapolation from three index sites to the whole glacier was compared by Reference March and TrabantMarch and Trabant (1996) to the detailed mapped winter balance and net firn and ice balance for 1966 and 1967. It was found for these two years the index sites were representative of the areas for which they are weighted in the balance model. The detailed firn and ice balance maps show the balance to be linear with elevation below the ELA and represented well by sites A and B. Though only slightly above the ELA, site D represents the whole accumulation zone well because it has a similar albedo to the rest of the accumulation zone throughout the melt season and because the winter balance gradient has a break in slope near the altitude of site D. If it were not for this break in the balance gradient, site D would probably have to be higher on the glacier to be representative of the accumulation zone or it would be necessary to change the weighting function.
The consistent methodology used on Gulkana Glacier is important to the accuracy of, and confidence in, the mass- balance record. A consistent program is less likely to produce errors in net balances that happen to sum to zero over the geodetic mass-balance intervals. Also, if the glaciological mass balance had been found to differ systematically from the geodetic mass balance, the consistent methodology would have enabled systematic adjustment of each net balance so the cumulative balances were in agreement. Without the consistent methodology, it would be difficult to apply a constant correction factor to the net balances.
4.2. Long-term response
The geodetic balances correspond to an average annual thinning rate of 0.31 m a-1 from 1974 to 1993 and 0.96 m a-1 from 1993 to 1999. This accelerated thinning rate in the 1990s has been observed nearly everywhere in Alaska (Reference Arendt, Echelmeyer, Harrison, Lingle and ValentineArendt and others, 2002). The more continuous cumulative glaciological balance record also shows these trends (Fig. 6).
The total thinning is greater near the terminus over the first period (Fig. 5). This is to be expected because of the longer time interval. From 1974 to 1993, maximum thinning was 60 m w.e., and during the second interval (1993-99) it was 40 m w.e. However, during the first interval, the surface elevation in the accumulation area changed little, whereas in the second interval, thinning in the accumulation area was 4 m w.e. Lower net accumulation rates in the accumulation area, accompanied by a general glacier velocity decrease, would lead to such trends.
5. Conclusions and Recommendations
The agreement of the results from two mass-balance methods on Gulkana Glacier is encouraging. It supports the use of a small number of index sites for determining the net glaciological balance if the required measurements and corrections are made meticulously. The glaciological mass balance of Gulkana Glacier can be represented accurately by three index sites, with only one accumulation area site located just above the average ELA. These results also demonstrate that the balance in a small radius can accurately describe the balance in an elevation band and that extrapolation with elevation and area can be done without causing large systematic errors in the glacier-wide cumulative mass-balance record.
These results do not necessarily apply to other glaciers or even to future measurements of Gulkana Glacier. Every glaciological mass-balance record needs to be calibrated regularly with the geodetic method. The glaciological method is ideal for annual measurements because it is easily used for seasonal balances and because it records point balances. The geodetic method is ideal for long-term (several years to decades) measurements because the errors associated with it are less time-dependent.
The featureless accumulation areas of many glaciers can account for large errors in the geodetic balances. The accumulation area on Gulkana Glacier is broken up into several small cirques with numerous nunataks and crevasses that aid stereo viewing. The snowline was also anomalously high during each year of photography, which provided good photographic contrast at high elevations. Relative control was excellent because the DEMs were made concurrently with numerous tie points. Ablation adjustments were calculated using a temporally and spatially tuned model.
Several precautions can produce more accurate comparisons and possible calibrations of the glaciological method. Photography should be taken as close as possible to the end of the balance year but before the occurrence of snow in the accumulation area. This will decrease the amount of error resulting from seasonal adjustments and improve stereo perception due to a minimum amount of snow at higher elevations. If possible, surveying mass-balance poles near the time of aerial photography will improve the determination of the balance between the time of photography and the end of the ablation season. An independent profile of the glacier surface is useful for checking the DEM. Measurement of changes in the total glacier area and time-variable AAD is also needed for an accurate comparison.
Acknowledgements
The USGS provided funding for the project. The authors would like to thank K. Echelmeyer, W. Harrison, M. Truffer and R. Motyka for many comments that improved the manuscript. A. Arendt also provided much assistance with figures and in revising the manuscript. Use of trade names in this report is for identification purposes only and does not constitute endorsement by the USGS.













