Introduction
It has long been recognized by engineers that the physical length of a strain-measuring instrument is extremely important when computing transients or cyclic strains (Reference Dove and AdamsDove and Adams, 1964, p. 195-241; Reference DallyDally and Riley, 1965, p. 399-421; Reference Murphy, Murphy and PetersonMurphy and others, 1957), In the case of a propagating dynamic strain pulse, the ratio of the strain-gauge length to the pulse length is critical, and totally fictitious results may be obtained if this is not taken into account. A gauge employed to measure the strain at a point on a standing sinusoidal oscillation will in fact measure the average strain over the gauge length. The error will depend on the ratio of the gauge length to the wavelength of the sinusoid.
This paper demonstrates another source of error which results from the measurement of a propagating strain wave by a rosette of three gauges. Three gauges in a rosette may be used to evaluate the principal strains and the directions of the axes of principal strain and it is this technique which is used to locate the direction of flexural waves travelling along the interface between sea ice and water. The waves are generated by an open-water sea swell impinging on the sea-ice boundary (Reference WadhamsWadhams, 1973; Reference Squire and AllanSquire and Allan, 1977). The method of rosette analysis though well-established in strain engineering is rarely applied to measure the effects of a propagating wave, and it was felt that a simple theoretical model of the system might yield some unexpected results. Using an elastic sheet on a fluid foundation, a dispersion equation is derived which permits a propagating wave. It is this wave which is used to investigate the feasibility of using a strain rosette to obtain directional information for the wave.
The data used in the experimental section were obtained using strainmeters originally developed at the Department of Geophysics, University of Cambridge, for the measurement of earth tides. The instruments were modified for use on ice (Reference Goodman, Goodman, Allan and BilhamGoodman and others, 1975) to a strainmeter of 2 m gauge length with decreased sensitivity. The experiments were carried out in Notre Dame Bay, Newfoundland as part of a joint venture between the Scott Polar Research Institute and C-CORE, Memorial University of Newfoundland.
Dispersion Equation
To a first approximation the flexural oscillations of sea ice due to ocean swell may be modelled by a thin elastic sheet resting on a fluid foundation of infinite depth (Reference Hendrickson and WebbHendrickson and Webb, 1963).

Fig. 1. Schematic diagram of wave in ice showing coordinate system.
With the coordinate system shown in Figure 1, the equation of the plate is (Reference HetényiHetényi, 1946)
where W(x, y, I) is the vertical displacement of the plate, P(x,y, t) $$$ is the pressure exerted on the plate by the fluid, $$$$ D = hŒji2{i—v2) $$$is the flexural rigidity of the plate, v is Poisson's ratio, E is Young's modulus, pi is the density of the plate, and h is the plate thickness. Values of E = 6.0 X io» N mz, v = 0.3, pi = 922.5 kg m-3 $$$ were chosen as appropriate values for sea ice.
Within the fluid we may define a velocity potential such that at every point Laplace's equation is satisfied (Reference StokerStoker, 1957).
At the ice/water interface we have two boundary conditions, the kinematical condition

and Bernoulli's equation
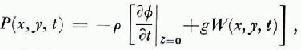
where p is the density of the fluid.
Hence the equation of motion is
Consider a plane-wave solution on$$$ z = 0 (Fig. 2)
where k is the wave number, n = (I, m) = (cos «, sin a) $$$ is the direction of propagation of the plane wave, r is the position of an arbitrary point on the plane wave front, and ω is the circular frequency.
Substitution into the equation of motion gives the required dispersion equation, a quintic polynomial in k.
We assume that the origin of coordinates is far from the ice edge so that any evanescent waves generated close to the edge (Reference Squire and AllanSquire and Allan, 1977) will have died away, k may therefore be regarded as real and positive.

Fig. 2. Plane wave front impinging on a delta rosette ABC with separation parameter a.
Principal Axes
Now the infinitesimal strain on the surface of the sea ice is given by
(Reference GraftGraft, 1975), so that

Consider the strain in some arbitrary direction β to the tf-axis,
Therefore,
Hence in directions A, B3 C (Fig. 2), the respective infinitesimal strains are


Fig. 3. Percentage error of strain measured by delta rosette as compared with single strainmeter in direction of impinging wave as a function of time increment for various ongles of attack. Wave period is 10 s, separation parameter a =o.o m.

Fig. 4. Predicted angle a as measured by delta rosette as a function of time increment for various angles of attack. Wave period is 10 s, separation parameter a = 0.0 m.
Suppose that the directions A, B, C represent the axes of a 120$$$0 strainmeter rosette. We choose a strainmeter of length 2 m, which corresponds to the instruments used in the experiments and allow a separation from the origin of a (Fig. 2).
Given three strains on a delta rosette $$$(1200 rosette, as discussed above) we may locate the axes of principal strain and compute the principal strains $$$$ fr and e2 as follows

where y is the angle between the axes of principal strain and one strainmeter of the strain rosette. After some algebra these equations lead to

The condition $$$|e,| J? 1-1 fixes the sign of $$$e,—c, and any ambiguity in the angle y.
Given an incident wave of particular period and angle of attack a, it is therefore possible to compare the expected surface strain and angle a with that calculated from the delta rosette. The percentage error in surface strain as a function of incremental time for a 10 s wave at angles of attack of o° through 6o° in steps of 10° is shown in Figure 3. The predicted angle $$ is shown for various angles of attack in Figure 4.
As the wave propagates past the strain rosette, each instrument will sample a different part of its cycle due to their physical separation. This will introduce a frequency-dependent phase difference between the strainmeters leading to the large errors (particularly where the strain goes through zero) shown in Figures 3 and 4. A choice of a — —1.0 m (half the physical length of the instrument) will eliminate the error completely, but it is not feasible experimentally to position the instrument in a star configuration with sufficient accuracy.
A monochromatic wave of known direction is not a realistic forcing and one might encounter a sea made up of waves and swell of many periods from several directions. The errors then become so unpredictable that continuous computation in the time domain is not a viable method for evaluating the direction of wave propagation and the associated principal strains.
Frequency-Domain Analysis
An alternative to time-series analysis is to compute a power spectral density for each strainmeter in the rosette every five minutes over several hours. From the power spectral density a root-mean-square strain about some centre frequency may be found by integration over a small frequency band-width and then taking the square root, A band-width of 5/320 Hz was used throughout. In this way the strain corresponding to discrete peaks in the power spectral density may be treated independently.
The power spectral densities were evaluated for data obtained over several hours on fast ice in Notre Dame Bay, Newfoundland, using a Hewlett-Packard 545 1B Fourier Analyser system located at Memorial University of Newfoundland (Reference Squire and AllanAllan and Squire, 1977). There were clear peaks at approximately 6 s and 13 s and it was the strains corresponding to these peaks which were used in the principal strain calculation. Figures 5 and 6 show the variation of the orientation of the axes of principal strain and the principal strains as a function of elapsed time for the recorded 10 h of data.
The mean and standard deviation of the orientation angle weighted with respect to the larger principal strain was found for both the long- and short-period components. For 112 samples the means of the two components were$$$ 2.40 and —13.6°$$$ respectively and the standard deviations, 7.8° and 7.3$$$0. A Student's /-test gave independent distributions with 99.9% confidence indicating that the waves were propagating from different directions and had originated from different sources. The predicted directions were the same as those observed visually over the duration of the experiment.

Fig. 5. Variation of orientation of principal axes of strain and principal strains/or long-period component over $$$JO h.

Fig. 6. Variation of orientation of principal axes of strain and principal strains far short-period component over l0h.
The orientation of the axes of principal strain with time depends upon the interference of the individual components of the wave spectrum. A predominant swell normal to the ice edge will generate a flexural wave travelling in the same direction. Waves impinging from other directions will interfere with the basic wave to produce a swing in the principal axes. This mechanism is a possible explanation for the parallel cracks which often form at an angle to the apparent incident swell during the wave break-up of sea ice. It also hints that a relationship between crack spacing and incident wavelength may not be as simple as was first imagined.
Discussion
In addition to the inaccuracies introduced by the physical length of a strain gauge we have found considerable errors due to the separation of the instruments in a strain rosette. Theoretically such errors may be removed by superposition of the instruments to form a star configuration but this is not feasible experimentally. Since most strain rosettes used at present in both mechanical and ice engineering do have their gauges separated by some small but finite distance it is very important to lake this into account when measuring propagating strain waves.
In geophysical applications, such as that described here, the random nature of the forcing makes it impossible to eliminate errors if the principal-axes approach is used. We have thus shown that it is essential to employ frequency-domain analysis for the treatment of data obtained by strainmeter rosettes.
Acknowledgements
This work was carried out while the author was in receipt of a research studentship from the Natural Environment Research Council of Great Britain, 1 am indebted to Dr Peter Wadhams and Alastair Allan for invaluable discussion. I also thank members of C-CORE and in particular the Twillingate field party whose cheerfulness and stimulating conversation led to a successful experiment.








