1 Introduction
1.1 Gradual typing
Gradual typing (Siek & Taha, Reference Siek and Taha2006) is a language feature designed to combine complementary benefits of static typing and dynamic typing languages. A gradual typing program allows the integration of dynamically typed code and statically typed code. While dynamically typed fragment requires additional runtime safety check as dynamic typing language, the statically typed fragment is guaranteed blame-free by the gradual type system. Thus, gradual typing enables developers to do rapid prototyping and seamlessly evolve into statically typed programs. Over the past decade, there have been many advances in gradual typing, both in academia and industry.
The academic field is mainly dedicated to combining gradual typing with other language features, including both expressiveness (object (Siek & Taha, Reference Siek and Taha2007; Chung et al., Reference Chung, Li, Nardelli and Vitek2018), effect (Bañados Schwerter et al., Reference Bañados Schwerter, Garcia and Tanter2014, Reference Bañados Schwerter, Garcia and Tanter2016;Wadler, Reference Wadler2021), polymorphism (Ahmed et al., Reference Ahmed, Findler, Siek and Wadler2011, Reference Ahmed, Jamner, Siek and Wadler2017; Igarashi et al., Reference Igarashi, Sekiyama and Igarashi2017), set theoretic types (Toro & Tanter, Reference Toro and Tanter2017; Castagna et al., Reference Castagna, Lanvin, Petrucciani and Siek2019)), and implementation optimization (Pycket (Bauman et al., Reference Bauman, Bolz, Hirschfeld, Kirilichev, Pape, Siek and Tobin-Hochstadt2015), Grift (Kuhlenschmidt et al., Reference Kuhlenschmidt, Almahallawi and Siek2019)).
In the industrial field, there are some practical gradually typed languages and optional type checkers. Practical gradually typed languages include including Typed Racket (Tobin-Hochstadt & Felleisen, Reference Tobin-Hochstadt and Felleisen2008), TypeScript (Bierman et al., Reference Bierman, Abadi and Torgersen2014), mypy (Lehtosalo et al., Reference Lehtosalo, van Rossum, Levkivskyi and Sullivan2014), Typed Clojure (Bonnaire-Sergeant et al., Reference Bonnaire-Sergeant, Davies and Tobin-Hochstadt2016), FLOW (Chaudhuri et al., Reference Chaudhuri, Vekris, Goldman, Roch and Levi2017), and so on. Most of them add unsound type systems to existing dynamically typed languages Footnote 1 .
1.2 A gradual type system hides erroneous data flows
A gradual type system can be viewed as a normal static type system with two extensions: a dynamic type
![]() $\star$
(also known as
$\star$
(also known as
![]() $?$
or Dyn) that represents dynamically typed code and a binary consistency relation that is used in place of equality to accommodate dynamic types in type rules. When only static types are involved, the consistency relation works the same as the type equality relation, while dynamic types are consistent with all types, which enables dynamically typed code to be integrated with statically typed code. However, the consistency relation is intransitive. For example, we have both
$?$
or Dyn) that represents dynamically typed code and a binary consistency relation that is used in place of equality to accommodate dynamic types in type rules. When only static types are involved, the consistency relation works the same as the type equality relation, while dynamic types are consistent with all types, which enables dynamically typed code to be integrated with statically typed code. However, the consistency relation is intransitive. For example, we have both
![]() $\mathrm{\texttt{Int}} \sim \star $
and
$\mathrm{\texttt{Int}} \sim \star $
and
![]() $\star \sim \mathrm{\texttt{Bool}}$
, but not
$\star \sim \mathrm{\texttt{Bool}}$
, but not
![]() $\mathrm{\texttt{Int}} \sim \mathrm{\texttt{Bool}}$
, since
$\mathrm{\texttt{Int}} \sim \mathrm{\texttt{Bool}}$
, since
![]() $\mathrm{\texttt{Int}} \neq \mathrm{\texttt{Bool}}$
in a static type system.
$\mathrm{\texttt{Int}} \neq \mathrm{\texttt{Bool}}$
in a static type system.
The consistency relation weakens the static type system, as a well-placed
![]() $\star$
can easily make a buggy program pass type checking. For example, consider the following STLC (Simply Typed Lambda Calculus) expression:
$\star$
can easily make a buggy program pass type checking. For example, consider the following STLC (Simply Typed Lambda Calculus) expression:
This program will be rejected by the static type system of STLC, and the result of running this program will be a dynamic type error, since a value of type Bool cannot be added to an integer value. However, in GTLC (Gradually Typed Lambda Calculus), this program will pass type checking if we change the type annotation from Int to
![]() $\star$
. As we state, we have both
$\star$
. As we state, we have both
![]() $\star \sim \mathrm{\texttt{Bool}}$
and
$\star \sim \mathrm{\texttt{Bool}}$
and
![]() $\star \sim \mathrm{\texttt{Int}}$
.
$\star \sim \mathrm{\texttt{Int}}$
.
Dynamic type is ubiquitous in many real-world gradually typed languages, where every omitted type annotation is treated as a dynamic type. To recover type soundness, a gradually typed language will check such dynamic inconsistency by runtime enforcement. The formal semantics of gradually typed language consists of two parts: (1) an independent statically typed intermediate language like blame calculus (Wadler & Findler, Reference Wadler and Findler2009), which extends the source gradually typed language with explicit type cast, and (2) a translation process, which inserts casts to the source program where consistency relation is used in static type checking.
A cast
![]() $\langle A \Leftarrow^b B \rangle v$
indicates that the guarded value v of type B is required to have type A, and this cast is identified with the blame label b. At runtime, casts in the translated program will catch dynamic inconsistency as cast error, and the responsible cast will be assigned blame. Such a mechanism is called blame tracking, derived from related research on contracts (Findler & Felleisen, Reference Findler and Felleisen2002; Tobin-Hochstadt et al., Reference Tobin-Hochstadt, Felleisen, Findler, Flatt, Greenman, Kent, St-Amour, Strickland and Takikawa2017). Compared with statically typed languages, the type safety property of gradually typed languages is characterized by blame behavior, which is one of the original results of Tobin-Hochstadt and Felleisen (Reference Tobin-Hochstadt and Felleisen2006) and subsequently improved in the follow-up research.
$\langle A \Leftarrow^b B \rangle v$
indicates that the guarded value v of type B is required to have type A, and this cast is identified with the blame label b. At runtime, casts in the translated program will catch dynamic inconsistency as cast error, and the responsible cast will be assigned blame. Such a mechanism is called blame tracking, derived from related research on contracts (Findler & Felleisen, Reference Findler and Felleisen2002; Tobin-Hochstadt et al., Reference Tobin-Hochstadt, Felleisen, Findler, Flatt, Greenman, Kent, St-Amour, Strickland and Takikawa2017). Compared with statically typed languages, the type safety property of gradually typed languages is characterized by blame behavior, which is one of the original results of Tobin-Hochstadt and Felleisen (Reference Tobin-Hochstadt and Felleisen2006) and subsequently improved in the follow-up research.
Informally, type safety of gradually typed languages ensures that every dynamic type error should be caught by a blame message. As a result, in a gradually typed programming language with type safety, a program without blame cannot go wrong. Every blame is triggered by a type cast failure, thus we can use the notion of the cast error to represent dynamic type error. In this paper, we equate dynamic type error and dynamic cast error for gradually typed languages, both of which represent type inconsistency detected at runtime.
The mentioned program 1 will be translated into the following program in blame calculus:
This program will abort with blame
![]() $b_1$
immediately after beta reduction.
$b_1$
immediately after beta reduction.
 \begin{align*} &(\lambda x:\star.\ (\langle \mathrm{\texttt{Int}} \Leftarrow^{b_1} \star \rangle x) + 1) \langle \star \Leftarrow^{b_2} \mathrm{\texttt{Bool}} \rangle \mathrm{\texttt{true}} \\ \longmapsto& (\langle \mathrm{\texttt{Int}} \Leftarrow^{b_1} \star \Leftarrow^{b_2} \mathrm{\texttt{Bool}} \rangle \mathrm{\texttt{true}}) + 1 \\ \longmapsto& \mathrm{\texttt{blame}}\ b_1 \end{align*}
\begin{align*} &(\lambda x:\star.\ (\langle \mathrm{\texttt{Int}} \Leftarrow^{b_1} \star \rangle x) + 1) \langle \star \Leftarrow^{b_2} \mathrm{\texttt{Bool}} \rangle \mathrm{\texttt{true}} \\ \longmapsto& (\langle \mathrm{\texttt{Int}} \Leftarrow^{b_1} \star \Leftarrow^{b_2} \mathrm{\texttt{Bool}} \rangle \mathrm{\texttt{true}}) + 1 \\ \longmapsto& \mathrm{\texttt{blame}}\ b_1 \end{align*}
This example shows that the consistency relation makes the gradual type system too weak to reject programs with even obvious type errors. Specifically, a gradual type system cannot detect erroneous data flows imposed by the passing of values during program execution. The inserted cast
![]() $\langle \mathrm{\texttt{Int}} \Leftarrow^{b_1} \star \rangle$
will be executed on every argument of the lambda expression, but a naive static analysis tells us that the only possible argument is a boolean that cast to dynamic. Therefore, this cast never succeeds—and the gradual type system cannot detect such a problem.
$\langle \mathrm{\texttt{Int}} \Leftarrow^{b_1} \star \rangle$
will be executed on every argument of the lambda expression, but a naive static analysis tells us that the only possible argument is a boolean that cast to dynamic. Therefore, this cast never succeeds—and the gradual type system cannot detect such a problem.
1.3 Our work: Static Blame
Recovery of data flows in gradual typing programs amounts to a more strict static check. However, we cannot simply reject a program if a hidden inconsistency is detected, since we cannot assert that the detected inconsistency will necessarily trigger a runtime error in the program. For example, it may be due to a commonly used idiom in dynamic languages: a dynamic parameter accepts values of multiple types and each control flow branch handles a different type (Castagna et al., Reference Castagna, Laurent, Nguyễn and Lutze2022). Therefore, there is a natural question as to how data flow relates to the results of running the program, and under what circumstances we can assert the existence of errors in gradual typing programs by detecting erroneous data flows.
One way to tackle this problem is from the blame mechanism. Data flows are monitored by type casts at runtime, and blame messages will be thrown when a cast fails. By the blame safety property, every dynamic error can be caught by a blame message. Therefore, if we can establish the correspondence between data flows and runtime blame information, then we can prove some properties of the runtime behavior indirectly through these data flows. Consider the following trivial example program:
where the meta-variable t represents a complicated computation hard to analyze statically. In this case, the hidden erroneous data flow is that a boolean value is passed as a dynamic value and cast to type int, but
![]() $\mathrm{\texttt{Int}} \not \sim \mathrm{\texttt{Bool}}$
. Although we cannot assert whether the program will abort with a blame message or not, we can still assert the cast
$\mathrm{\texttt{Int}} \not \sim \mathrm{\texttt{Bool}}$
. Although we cannot assert whether the program will abort with a blame message or not, we can still assert the cast
![]() $\langle \mathrm{\texttt{Int}} \Leftarrow \star \rangle$
that will be inserted to the else branch is erroneous. This is because the only value passed into x is of type Bool.
$\langle \mathrm{\texttt{Int}} \Leftarrow \star \rangle$
that will be inserted to the else branch is erroneous. This is because the only value passed into x is of type Bool.
With this principle, we introduce Static Blame in this paper, a framework for establishing the correspondence between static-time data flow information and runtime behavior for gradually typed programs. As its name suggests, the goal of Static Blame is to determine possible runtime blame messages of a program at static time, enabling a more rigorous static check than type checking.
The key concept of Static Blame is type flow, which gives a uniform treatment to type casts and flow constraints. As the standard flow constraints, type flow models the value passing relation among the contexts of a program, while type casts can be viewed as special value passing monitored by blame mechanism. By intuition, a type flow
![]() $\hat{T} \triangleright_b \hat{S}$
denotes that values in context
$\hat{T} \triangleright_b \hat{S}$
denotes that values in context
![]() $\hat{T}$
may flow into context
$\hat{T}$
may flow into context
![]() $\hat{S}$
during program execution.
$\hat{S}$
during program execution.
![]() $\hat{T}$
(resp.
$\hat{T}$
(resp.
![]() $\hat{S}$
) is a labeled type, which is used to formalize the notion of runtime context, as the standard technique program labels (Nielson et al., Reference Nielson, Nielson and Hankin1999). Moreover, we say that
$\hat{S}$
) is a labeled type, which is used to formalize the notion of runtime context, as the standard technique program labels (Nielson et al., Reference Nielson, Nielson and Hankin1999). Moreover, we say that
![]() $\hat{T}$
is an inflow of
$\hat{T}$
is an inflow of
![]() $\hat{S}$
, while
$\hat{S}$
, while
![]() $\hat{S}$
is an outflow of
$\hat{S}$
is an outflow of
![]() $\hat{T}$
. With type flow, Static Blame can reveal data flows mediated by dynamic types by type flow analysis, which consists of a generation process and a transitivity analysis. We develop Static Blame on a standard formal gradual typing lambda calculus
$\hat{T}$
. With type flow, Static Blame can reveal data flows mediated by dynamic types by type flow analysis, which consists of a generation process and a transitivity analysis. We develop Static Blame on a standard formal gradual typing lambda calculus
![]() $\lambda_\star$
, an extension of GTLC by adding subtyping relation. It bears strong resemblance to the language
$\lambda_\star$
, an extension of GTLC by adding subtyping relation. It bears strong resemblance to the language
![]() $\mathbf{Ob}^?_{<:}$
in Siek and Taha (Reference Siek and Taha2007), albeit without object-oriented features. Its runtime semantics is defined by a translation process into a blame calculus
$\mathbf{Ob}^?_{<:}$
in Siek and Taha (Reference Siek and Taha2007), albeit without object-oriented features. Its runtime semantics is defined by a translation process into a blame calculus
![]() $\lambda_B$
, which admits a standard Natural semantics
Footnote 2
of gradually typed languages.
$\lambda_B$
, which admits a standard Natural semantics
Footnote 2
of gradually typed languages.
The form of the type flow is designed to be similar to type casts in blame calculus and indicate a direct correspondence between type flows and type casts. With the formal system that will be developed later, every type cast
![]() $\langle S\Leftarrow^b T\rangle$
occurring in the execution corresponds directly to a type flow
$\langle S\Leftarrow^b T\rangle$
occurring in the execution corresponds directly to a type flow
![]() $\hat{T} \triangleright_b \hat{S}$
. The type flow analysis ensures that for every possible type cast combination
$\hat{T} \triangleright_b \hat{S}$
. The type flow analysis ensures that for every possible type cast combination
![]() $\langle S\Leftarrow^{b_1} G\rangle \langle G \Leftarrow^{b_2} T\rangle $
occurring in the execution, there will be type flows
$\langle S\Leftarrow^{b_1} G\rangle \langle G \Leftarrow^{b_2} T\rangle $
occurring in the execution, there will be type flows
![]() $\hat{G} \triangleright_{b_1} \hat{S}, \hat{T} \triangleright_{b_2} \hat{G}$
generated by type flow analysis. As a result, Static Blame can exploit the possible failure of a gradually typed program statically.
$\hat{G} \triangleright_{b_1} \hat{S}, \hat{T} \triangleright_{b_2} \hat{G}$
generated by type flow analysis. As a result, Static Blame can exploit the possible failure of a gradually typed program statically.
However, flow analysis requires minor changes to fit in gradually typed languages. The compilation and evaluation of a gradually typed program will generate cast expressions that are not presented in the source code, which therefore cannot be simply denoted by certain textual positions in the source code. For example, in the blame calculus, the evaluation of term application v’ w involves a cast decomposition when the applied term v’ is a cast
![]() $\langle T_1 \to S_2 \Leftarrow^b S_1 \to T_2 \rangle v$
between function types.
$\langle T_1 \to S_2 \Leftarrow^b S_1 \to T_2 \rangle v$
between function types.
The sub-expression
![]() $(\langle T_2 \Leftarrow^b T_1 \rangle w)$
inside the right hand is newly generated and cannot be viewed as an evaluation result of any proper sub-expression inside the left hand. As a result, labeled types encode more information than program labels. Besides a textual identifier, a labeled type
$(\langle T_2 \Leftarrow^b T_1 \rangle w)$
inside the right hand is newly generated and cannot be viewed as an evaluation result of any proper sub-expression inside the left hand. As a result, labeled types encode more information than program labels. Besides a textual identifier, a labeled type
![]() $\hat{T}$
also carries a gradual type T and a list (maybe empty) of context refinements to indicate these new contexts. The carried type T in
$\hat{T}$
also carries a gradual type T and a list (maybe empty) of context refinements to indicate these new contexts. The carried type T in
![]() $\hat{T}$
is just a designed redundancy to keep the similarity between type flow and type cast in form.
$\hat{T}$
is just a designed redundancy to keep the similarity between type flow and type cast in form.
1.4 Potential error and error classification
To demonstrate the effects of the Static Blame framework, we also develop a classification of potential errors detected from type flow analysis and prove formal properties of each category in the classification. Generally speaking, for a type flow
![]() $\hat{\star}_1 \triangleright_{b_1} \hat{S}$
gotten in type flow analysis, if there is also a type flow
$\hat{\star}_1 \triangleright_{b_1} \hat{S}$
gotten in type flow analysis, if there is also a type flow
![]() $\hat{T} \triangleright_{b_2} \triangleright \hat{\star}_2$
such that
$\hat{T} \triangleright_{b_2} \triangleright \hat{\star}_2$
such that
![]() $T \not \sim S$
and
$T \not \sim S$
and
![]() $\hat{\star}_1 = \hat{\star}_2$
, then a potential error is detected. In other words, a potential error is an inconsistent flow via dynamic types. Specifically, we classify detected potential errors into three categories in a way similar to may-must information (Nielson et al., Reference Nielson, Nielson and Hankin1999) in software analysis. Namely,
$\hat{\star}_1 = \hat{\star}_2$
, then a potential error is detected. In other words, a potential error is an inconsistent flow via dynamic types. Specifically, we classify detected potential errors into three categories in a way similar to may-must information (Nielson et al., Reference Nielson, Nielson and Hankin1999) in software analysis. Namely,
1. normal potential errors for type flows that may be an erroneous data flow.
2. strict potential errors for type flows that must be an erroneous data flow.
3. wrong dynamic types for dynamic types that always hide erroneous data flows.
For example, consider the following example program as a variant of expression: 3:
In the compiled blame calculus code, any value passed to x will be cast to a boolean by
![]() $\langle \mathrm{\texttt{Bool}} \Leftarrow \star \rangle x$
in the
$\langle \mathrm{\texttt{Bool}} \Leftarrow \star \rangle x$
in the
![]() $\neg x$
and to an integer by
$\neg x$
and to an integer by
![]() $\langle \mathrm{\texttt{Int}} \Leftarrow \star \rangle x$
in the
$\langle \mathrm{\texttt{Int}} \Leftarrow \star \rangle x$
in the
![]() $x + 1$
. Suppose that these two type casts correspond to type flows
$x + 1$
. Suppose that these two type casts correspond to type flows
![]() $\hat{\star} \triangleright_{b_1} \hat{\mathrm{\texttt{Bool}}}$
and
$\hat{\star} \triangleright_{b_1} \hat{\mathrm{\texttt{Bool}}}$
and
![]() $\hat{\star} \triangleright_{b_2} \hat{\mathrm{\texttt{Int}}}$
where
$\hat{\star} \triangleright_{b_2} \hat{\mathrm{\texttt{Int}}}$
where
![]() $\hat{\star}$
denotes the labeled type of x, then we can induce that:
$\hat{\star}$
denotes the labeled type of x, then we can induce that:
1. if there exists an inflow of type T inconsistent with Bool (resp. Int) via
 $\hat{\star}$
, the type flow
$\hat{\star}$
, the type flow
 $\hat{\star} \triangleright_{b_1} \hat{\mathrm{\texttt{Bool}}}$
(resp.
$\hat{\star} \triangleright_{b_1} \hat{\mathrm{\texttt{Bool}}}$
(resp.
 $\hat{\star} \triangleright_{b_2} \hat{\mathrm{\texttt{Int}}}$
) may fail;
$\hat{\star} \triangleright_{b_2} \hat{\mathrm{\texttt{Int}}}$
) may fail;2. if every inflow via
 $\hat{\star}$
is inconsistent with Bool (resp. Int), the type flow
$\hat{\star}$
is inconsistent with Bool (resp. Int), the type flow
 $\hat{\star} \triangleright_{b_1} \hat{\mathrm{\texttt{Bool}}}$
(resp.
$\hat{\star} \triangleright_{b_1} \hat{\mathrm{\texttt{Bool}}}$
(resp.
 $\hat{\star} \triangleright_{b_2} \hat{\mathrm{\texttt{Int}}}$
) must fail;
$\hat{\star} \triangleright_{b_2} \hat{\mathrm{\texttt{Int}}}$
) must fail;3. if each inflow of
 $\hat{\star}$
is inconsistent with each outflow of
$\hat{\star}$
is inconsistent with each outflow of
 $\hat{\star}$
,
$\hat{\star}$
,
 $\hat{\star}$
is a wrong dynamic type.
$\hat{\star}$
is a wrong dynamic type.
The correspondence of type flow and type cast by the Static Blame framework guarantees several formal properties of our classification. For normal potential errors, we prove that the detection is complete, namely if no normal potential error is detected in a program, then no cast can fail at runtime, implying that the program will not abort with any blame. In other words, every type cast that fails at runtime will be reported as a normal potential error.
As we explained earlier, a detected potential error is not guaranteed to lead to an actual runtime cast failure. Therefore, the detection of normal potential errors is not sound, and mere completeness is a weak property. Note that it is also complete to naively treat every cast as a potential error. In contrast, the detection of strict potential errors is more precise. We claim that strict potential errors are sound with respect to erroneous type casts, whereas erroneous type casts are type casts that can never succeed.
The main difficulty of proof is how to define erroneous type casts formally. An intuitive attempt is to state that every program with erroneous type casts must abort with a blame message. But a cast inserted in the compiled gradual typing program may not execute. Moreover, a higher-order cast will not trigger a cast failure until it is used.
Therefore, we define erroneous type cast with respect to its runtime execution and prove that if an erroneous type cast is executed at runtime, then the whole program must abort with a blame message in one or more steps. Then, we can conclude our claim with a proof that strict potential error is sound with respect to erroneous type casts under the correspondence developed by the Static Blame framework.
Finally, a wrong dynamic type is a labeled dynamic type that always hides wrong data flows, which means that every non-dynamic inflow is inconsistent with every non-dynamic outflow. We will show that every non-dynamic outflow is a strict potential error. With the soundness of strict potential error, running a gradual typing program will immediately abort with a blame message whenever a value of wrong dynamic type is used. Or, values that are held in wrong dynamic types (recall that labeled types represent contexts) can never be safely used.
The notion of type flow and correspondence originated from a previous work of Rastogi et al. (Reference Rastogi, Chaudhuri and Hosmer2012). The goal of their work is also known as automatic type migration now. That is, they tried to infer a more precise type for every dynamic type in source code, and not reject any statically well-typed program. A more detailed comparison between our work and studies on type migration is presented in Section 6.
Our contributions are summarized as follows:
• We propose the Static Blame framework on a standard gradually typed language
 $\lambda_\star$
. Static blame establishes the correspondence between static-time data flow information and runtime behavior for gradually typed programs. It consists of three parts: the concepts labeled type and type flow, which give a uniform treatment to type cast and data flow relations (Section 3.1); type flow analysis, a method to generate type flows by transitivity analysis (Section 3.2); flow-cast correspondence, a direct correspondence between type flows and type casts for a
$\lambda_\star$
. Static blame establishes the correspondence between static-time data flow information and runtime behavior for gradually typed programs. It consists of three parts: the concepts labeled type and type flow, which give a uniform treatment to type cast and data flow relations (Section 3.1); type flow analysis, a method to generate type flows by transitivity analysis (Section 3.2); flow-cast correspondence, a direct correspondence between type flows and type casts for a
 $\lambda_\star$
program (Section 3.3).
$\lambda_\star$
program (Section 3.3).• We present a practical application of Static Blame by detecting potential errors from type flow analysis. We successfully characterize how potential errors affect program execution by classifying detected potential errors into three categories and proving formal properties of them, including: completeness of normal potential error (Section 4.1); soundness up to erroneous casts of strict potential error (Section 4.2); and inhabitants of wrong dynamic types are unsafe to use (Section 4.3).
• We implemented a bug detector SLOG (Static Blame fOr Grift) based Static Blame on Grift, a gradually typed variant of STLC (Section 5.1.1). We evaluated SLOG on a benchmark generated by mutation analysis from the original benchmark of Grift (Section 5.3). The effectiveness of Static Blame is validated that SLOG can successfully detect potential errors, and its performance is acceptable for programs of small and medium sizes within two or three thousand lines of code (Section 5.4). The implementation and data are publicly available Footnote 3 .
The rest of this paper is organized as follows. Section 2 introduces the syntax and semantics of a gradually typed language, including a surface language
![]() $\lambda_\star$
and an intermediate language
$\lambda_\star$
and an intermediate language
![]() $\lambda_B$
. Section 3 introduces the formal definition of the Static Blame framework. Section 4 develops the detection and classification of potential errors based on Static Blame. Section 5 evaluates effectiveness and performance of Static Blame. Section 6 reviews related work.
$\lambda_B$
. Section 3 introduces the formal definition of the Static Blame framework. Section 4 develops the detection and classification of potential errors based on Static Blame. Section 5 evaluates effectiveness and performance of Static Blame. Section 6 reviews related work.
2 Background: Program syntax and semantics
In this section, we give formal definitions of the gradual typing lambda calculus
![]() $\lambda_\star$
and blame calculus
$\lambda_\star$
and blame calculus
![]() $\lambda_B$
. The blame calculus
$\lambda_B$
. The blame calculus
![]() $\lambda_B$
is not space-efficient (Herman et al., Reference Herman, Tomb and Flanagan2010), allowing unbounded accumulation of runtime casts, to simplify development and proof of relevant properties. This choice does not impair the validity of our framework, since space-efficient semantics can be designed equivalent to a normal semantic (Siek & Wadler, Reference Siek and Wadler2010; Siek et al., Reference Siek, Vitousek, Cimini, Tobin-Hochstadt and Garcia2015).
$\lambda_B$
is not space-efficient (Herman et al., Reference Herman, Tomb and Flanagan2010), allowing unbounded accumulation of runtime casts, to simplify development and proof of relevant properties. This choice does not impair the validity of our framework, since space-efficient semantics can be designed equivalent to a normal semantic (Siek & Wadler, Reference Siek and Wadler2010; Siek et al., Reference Siek, Vitousek, Cimini, Tobin-Hochstadt and Garcia2015).
2.1 Syntax
The syntax of
![]() $\lambda_B$
and
$\lambda_B$
and
![]() $\lambda_\star$
are both given in figure 1. Since
$\lambda_\star$
are both given in figure 1. Since
![]() $\lambda_B$
is an extension of
$\lambda_B$
is an extension of
![]() $\lambda_\star$
, they share some common syntactic categories. The parts without highlighting are common to both of them, the light-gray highlighted part belongs to
$\lambda_\star$
, they share some common syntactic categories. The parts without highlighting are common to both of them, the light-gray highlighted part belongs to
![]() $\lambda_B$
, and the gray highlighted part belongs to
$\lambda_B$
, and the gray highlighted part belongs to
![]() $\lambda_\star$
. In other words,
$\lambda_\star$
. In other words,
![]() $\lambda_B$
extends
$\lambda_B$
extends
![]() $\lambda_\star$
by substituting light-gray part for dark-gray part in
$\lambda_\star$
by substituting light-gray part for dark-gray part in
![]() $\lambda_\star$
. In this paper, the denotation of shared syntactic symbols will be clear from context.
$\lambda_\star$
. In this paper, the denotation of shared syntactic symbols will be clear from context.

Fig. 1. Syntax of
![]() $\lambda_\star$
and
$\lambda_\star$
and
![]() $\lambda_B.$
$\lambda_B.$
We let G,T or S range over types. A gradual type is either a base type
![]() $\iota$
, the dynamic type
$\iota$
, the dynamic type
![]() $\star$
, a function type
$\star$
, a function type
![]() $T \to S$
, or a record type
$T \to S$
, or a record type
![]() $\{\overline{l_i : G_i} \}$
. Each field label l belongs to a countably infinite set
$\{\overline{l_i : G_i} \}$
. Each field label l belongs to a countably infinite set
![]() $\mathcal{L}$
, which is assumed to be disjoint with other syntactic categories. With subscripted
$\mathcal{L}$
, which is assumed to be disjoint with other syntactic categories. With subscripted
![]() $\star$
, type metavariables
$\star$
, type metavariables
![]() $G_\star,T_\star$
and
$G_\star,T_\star$
and
![]() $S_\star$
indicate gradual types that are not
$S_\star$
indicate gradual types that are not
![]() $\star$
. Note that types like
$\star$
. Note that types like
![]() $\star \to \star,\{l:\star\}$
are still
$\star \to \star,\{l:\star\}$
are still
![]() $G_\star$
types. We give an inductive definition of them in Figure 1. We let x,y,z range over term variables, which belong to another countably infinite set
$G_\star$
types. We give an inductive definition of them in Figure 1. We let x,y,z range over term variables, which belong to another countably infinite set
![]() $\mathcal{V}$
. We let t range over terms, and e,s range over expressions.
$\mathcal{V}$
. We let t range over terms, and e,s range over expressions.
An expression is a term with a context label attached to it. In the source code of a gradually typed programming language, a context label is merely a syntactical program label
![]() $\omega$
which belongs to another denumerable set
$\omega$
which belongs to another denumerable set
![]() $\Omega$
. In the semantics Section 2.2, we will explore how context labels can be employed to identify and subsequently track the evaluation of expressions in the source code. Importantly, context labels have no impact on the semantics of
$\Omega$
. In the semantics Section 2.2, we will explore how context labels can be employed to identify and subsequently track the evaluation of expressions in the source code. Importantly, context labels have no impact on the semantics of
![]() $\lambda_B$
. In Section 3, context labels play a fundamental role in Static Blame as the definition of type flow is based on them. Consequently, the entire type flow analysis algorithm relies on context labels.
$\lambda_B$
. In Section 3, context labels play a fundamental role in Static Blame as the definition of type flow is based on them. Consequently, the entire type flow analysis algorithm relies on context labels.
A context label also contains a list of context refinements to denote newly generated contexts during compilation and evaluation, the precise meaning will be explained later in the semantics Section 2.2.
A term may be a variable x, a constant c, a lambda expression
![]() $\lambda x:G. e$
, an application
$\lambda x:G. e$
, an application
![]() $e_1 e_2$
, a record
$e_1 e_2$
, a record
![]() $\{\overline{l_i = e_i} \}$
, a record projection
$\{\overline{l_i = e_i} \}$
, a record projection
![]() $e.l$
, or a conditional expression
$e.l$
, or a conditional expression
![]() $\mathrm{\texttt{if}}\ e_1\ \mathrm{\texttt{then}}\ e_2\ \mathrm{\texttt{else}}\ e_3$
.
$\mathrm{\texttt{if}}\ e_1\ \mathrm{\texttt{then}}\ e_2\ \mathrm{\texttt{else}}\ e_3$
.
Terms of
![]() $\lambda_\star$
also contain ascription
$\lambda_\star$
also contain ascription
![]() $e :: G$
, which does not exist in the blame calculus
$e :: G$
, which does not exist in the blame calculus
![]() $\lambda_B$
. Ascriptions denote manual type casts by programmers and will be replaced by explicit type casts in
$\lambda_B$
. Ascriptions denote manual type casts by programmers and will be replaced by explicit type casts in
![]() $\lambda_B$
during translation. A type cast
$\lambda_B$
during translation. A type cast
![]() $\langle S \Leftarrow^b T \rangle e $
denotes casting the type of term t from T to S at run-time and is identified by a blame label b which is also a program label. In this paper,
$\langle S \Leftarrow^b T \rangle e $
denotes casting the type of term t from T to S at run-time and is identified by a blame label b which is also a program label. In this paper,
![]() $\langle T_1 \Leftarrow^{b_1} T_2 \Leftarrow^{b_2} T_3 ... T_n \Leftarrow^{b_n} T_{n+1} \rangle$
is an abbreviation of the sequence of casts
$\langle T_1 \Leftarrow^{b_1} T_2 \Leftarrow^{b_2} T_3 ... T_n \Leftarrow^{b_n} T_{n+1} \rangle$
is an abbreviation of the sequence of casts
![]() $ \langle T_1 \Leftarrow^{b_1} T_2 \rangle \langle T_2 \Leftarrow^{b_2} T_3 \rangle ... \langle T_n \Leftarrow^{b_n} T_{n+1} \rangle$
. Whenever employing this abbreviation, we will provide further clarification if it is not trivial to omit context labels.
$ \langle T_1 \Leftarrow^{b_1} T_2 \rangle \langle T_2 \Leftarrow^{b_2} T_3 \rangle ... \langle T_n \Leftarrow^{b_n} T_{n+1} \rangle$
. Whenever employing this abbreviation, we will provide further clarification if it is not trivial to omit context labels.
The reuse of context label as blame label is nothing deep. It is just a convenient way to make the compilation process deterministic, which needs to generate fresh blame label to identify different type casts occurring in the compiled program. The blame label itself is just an identifier to distinguish different casts without additional semantics. Therefore, the main task of the blame label generation process is to ensure that different casts have different blame labels in the compilation result (see Proposition 2.9).
We also assume a denumerable set of constants as the definition of blame calculus of Walder and Findler (2009). Constants include values of base types and operations on them. Therefore, each constant is static. Specifically, We assume a meta function ty that maps every constant to its predefined type in the standard way. For example,
![]() $ty(\mathrm{\texttt{true}})$
and
$ty(\mathrm{\texttt{true}})$
and
![]() $ty(\mathrm{\texttt{false}})$
are defined as type Bool, while
$ty(\mathrm{\texttt{false}})$
are defined as type Bool, while
![]() $ty(+)$
and
$ty(+)$
and
![]() $ty(-)$
are defined as
$ty(-)$
are defined as
![]() $\mathrm{\texttt{Int}} \to \mathrm{\texttt{Int}} \to \mathrm{\texttt{Int}}$
. Being static means that for any constant c, the type ty(c) does not contain any
$\mathrm{\texttt{Int}} \to \mathrm{\texttt{Int}} \to \mathrm{\texttt{Int}}$
. Being static means that for any constant c, the type ty(c) does not contain any
![]() $\star$
within it.
$\star$
within it.
Since
![]() $\lambda_\star$
is a gradually typed language extended by subtyping relation, consistent subtyping
$\lambda_\star$
is a gradually typed language extended by subtyping relation, consistent subtyping
![]() $T <' S$
is used in typing rules rather than consistency. The declarative definition of consistent subtyping is given in Figure 1 along with standard consistency. The distinction between
$T <' S$
is used in typing rules rather than consistency. The declarative definition of consistent subtyping is given in Figure 1 along with standard consistency. The distinction between
![]() $T <' S$
and consistency is the width subtyping rule for records.
$T <' S$
and consistency is the width subtyping rule for records.
Consistency is a structural relation. A base type is consistent with itself. A dynamic type is consistent with every type. Two function types are consistent if their domains and ranges are consistent. Two record types are consistent if they have the same fields and their fields are consistent. We refer to Garcia et al. (Reference Garcia, Clark and Tanter2016) for more details about the design principle of consistency relation.
The consistent subtyping relation merely extends standard subtyping relation with two additional rules stating that a dynamic type
![]() $\star$
satisfies consistent subtyping with any gradual type in both directions. This definition shows that consistent subtyping is mostly a structural relation.
$\star$
satisfies consistent subtyping with any gradual type in both directions. This definition shows that consistent subtyping is mostly a structural relation.
![]() $T <' S$
if every pair (T’,S’) of corresponding parts in type trees of T and S satisfies subtyping relation or one of them is
$T <' S$
if every pair (T’,S’) of corresponding parts in type trees of T and S satisfies subtyping relation or one of them is
![]() $\star$
. We refer to Xie et al. (Reference Xie, Bi, d. S. Oliveira and Schrijvers2020) for a fairly comprehensive research of consistent subtyping.
$\star$
. We refer to Xie et al. (Reference Xie, Bi, d. S. Oliveira and Schrijvers2020) for a fairly comprehensive research of consistent subtyping.
Figure 2 describes the static type system and translation relation of
![]() $\lambda_\star$
simultaneously. By omitting the highlighted parts, it defines the type system of
$\lambda_\star$
simultaneously. By omitting the highlighted parts, it defines the type system of
![]() $\lambda_\star$
as a ternary relation
$\lambda_\star$
as a ternary relation
![]() $\Gamma \vdash e : G$
. And by adding the highlighted parts, it defines the translation static semantics as a relation
$\Gamma \vdash e : G$
. And by adding the highlighted parts, it defines the translation static semantics as a relation
![]() $\Gamma \vdash t \rightsquigarrow s : G$
, where s denotes terms in
$\Gamma \vdash t \rightsquigarrow s : G$
, where s denotes terms in
![]() $\lambda_B$
.
$\lambda_B$
.

Fig. 2. Static semantics of
![]() $\lambda_\star.$
$\lambda_\star.$
We let
![]() $\Gamma$
range over type environments, which are partial functions that map term variables into gradual types and are represented by unordered sets of pairs
$\Gamma$
range over type environments, which are partial functions that map term variables into gradual types and are represented by unordered sets of pairs
![]() $x:G$
. The extension of type environment
$x:G$
. The extension of type environment
![]() $\Gamma,(x:G)$
is an abbreviation of set union, where we assume the new variable x is not in the domain of
$\Gamma,(x:G)$
is an abbreviation of set union, where we assume the new variable x is not in the domain of
![]() $\Gamma$
.
$\Gamma$
.
There are two points we need to clarify in Figure 2. First, the rule T_If involves a join operator
![]() $\vee$
ensuring that branches of a conditional expression can have different types.
$\vee$
ensuring that branches of a conditional expression can have different types.
Definition 2.1 (
![]() $\vee$
and
$\vee$
and
![]() $\wedge$
). The operation
$\wedge$
). The operation
![]() $\vee$
and
$\vee$
and
![]() $\wedge$
is defined as
$\wedge$
is defined as
 \begin{align*} &\star \vee G = G \vee \star = \star \quad \star \wedge G = G \wedge \star = G \quad \iota \vee \iota = \iota \wedge \iota = \iota \\ &(T_{11} \to T_{12}) \vee (T_{21} \to T_{22}) = (T_{11} \wedge T_{21}) \to (T_{12} \vee T_{22}) \\ &(T_{11} \to T_{12}) \wedge (T_{21} \to T_{22}) = (T_{11} \vee T_{21}) \to (T_{12} \wedge T_{22}) \\ &\{ \overline{l_i:T_{i1}}, \overline{l_j:T_j} \} \vee \{ \overline{l_i:T_{i2}}, \overline{l_k:T_k} \} = \{ \overline{l_i:T_{i1} \vee T_{i2}}\} &\mathrm{, where }\{\overline{l_j}\} \cap \{\overline{l_k}\} = \emptyset \\ &\{ \overline{l_i:T_{i1}}, \overline{l_j:T_j} \} \wedge \{ \overline{l_i:T_{i2}}, \overline{l_k:T_k} \} = \{ \overline{l_i:T_{i1} \wedge T_{i2}}, \overline{l_j:T_j}, \overline{l_k:T_k} \} &\mathrm{, where }\{\overline{l_j}\} \cap \{\overline{l_k}\} = \emptyset \\\end{align*}
\begin{align*} &\star \vee G = G \vee \star = \star \quad \star \wedge G = G \wedge \star = G \quad \iota \vee \iota = \iota \wedge \iota = \iota \\ &(T_{11} \to T_{12}) \vee (T_{21} \to T_{22}) = (T_{11} \wedge T_{21}) \to (T_{12} \vee T_{22}) \\ &(T_{11} \to T_{12}) \wedge (T_{21} \to T_{22}) = (T_{11} \vee T_{21}) \to (T_{12} \wedge T_{22}) \\ &\{ \overline{l_i:T_{i1}}, \overline{l_j:T_j} \} \vee \{ \overline{l_i:T_{i2}}, \overline{l_k:T_k} \} = \{ \overline{l_i:T_{i1} \vee T_{i2}}\} &\mathrm{, where }\{\overline{l_j}\} \cap \{\overline{l_k}\} = \emptyset \\ &\{ \overline{l_i:T_{i1}}, \overline{l_j:T_j} \} \wedge \{ \overline{l_i:T_{i2}}, \overline{l_k:T_k} \} = \{ \overline{l_i:T_{i1} \wedge T_{i2}}, \overline{l_j:T_j}, \overline{l_k:T_k} \} &\mathrm{, where }\{\overline{l_j}\} \cap \{\overline{l_k}\} = \emptyset \\\end{align*}
If defined,
![]() $T \vee S$
is a common consistent supertype of T and S, while
$T \vee S$
is a common consistent supertype of T and S, while
![]() $T \wedge S$
is a common consistent subtype of T and S.
$T \wedge S$
is a common consistent subtype of T and S.
Proposition 2.2. For every gradual types T and S,
1. if
 $T \vee S$
is defined, then
$T \vee S$
is defined, then
 $T <' T \vee S$
and
$T <' T \vee S$
and
 $S <' T \vee S$
;
$S <' T \vee S$
;2. if
 $T \wedge S$
is defined, then
$T \wedge S$
is defined, then
 $T \wedge S <' T$
and
$T \wedge S <' T$
and
 $T \wedge S <' S$
.
$T \wedge S <' S$
.
Second, the translation process requires context refinement by
![]() $\blacktriangleleft$
for every newly generated sub-expression. The symbol
$\blacktriangleleft$
for every newly generated sub-expression. The symbol
![]() $\blacktriangleleft$
is used for cast expressions. The expression with the label
$\blacktriangleleft$
is used for cast expressions. The expression with the label
![]() $p\blacktriangleleft$
will be cast to the expression with label p. For example, in T_App the argument expression
$p\blacktriangleleft$
will be cast to the expression with label p. For example, in T_App the argument expression
![]() $e_2$
in
$e_2$
in
![]() $\lambda_\star$
is assumed to be translated to an expression
$\lambda_\star$
is assumed to be translated to an expression
![]() $t_2^{\,p_2}$
, and a cast is inserted to form a new argument expression
$t_2^{\,p_2}$
, and a cast is inserted to form a new argument expression
![]() $(\langle T_1 \Leftarrow^{\,p_2} T_2 \rangle t_2^{\,p_2\blacktriangleleft})^{\,p_2}$
in
$(\langle T_1 \Leftarrow^{\,p_2} T_2 \rangle t_2^{\,p_2\blacktriangleleft})^{\,p_2}$
in
![]() $\lambda_B$
. We let the new argument expression keep the label
$\lambda_B$
. We let the new argument expression keep the label
![]() $p_2$
after translation. To maintain the uniqueness of context labels (Proposition 2.9), the label of the term
$p_2$
after translation. To maintain the uniqueness of context labels (Proposition 2.9), the label of the term
![]() $t_2$
is a refined label
$t_2$
is a refined label
![]() $p_2\blacktriangleleft$
, which means “the value of this expression will be cast to the value of
$p_2\blacktriangleleft$
, which means “the value of this expression will be cast to the value of
![]() $p_2$
”. Similarly in T_AppDyn and T_If, this kind of context refinement by
$p_2$
”. Similarly in T_AppDyn and T_If, this kind of context refinement by
![]() $\blacktriangleleft$
happens where casts are inserted. Note that T_Ann does not need context refinement, since an ascription is directly transformed into a cast and no new sub-expression is generated. Other type rules are standard.
$\blacktriangleleft$
happens where casts are inserted. Note that T_Ann does not need context refinement, since an ascription is directly transformed into a cast and no new sub-expression is generated. Other type rules are standard.
Definition 2.3 (sub-expressions and
![]() $\mathfrak{S}(e)$
). The sub-expressions of an expression e in
$\mathfrak{S}(e)$
). The sub-expressions of an expression e in
![]() $\lambda_\star$
or
$\lambda_\star$
or
![]() $\lambda_B$
, denoted by
$\lambda_B$
, denoted by
![]() $\mathfrak{S}(e)$
, is a multi-set defined by
$\mathfrak{S}(e)$
, is a multi-set defined by
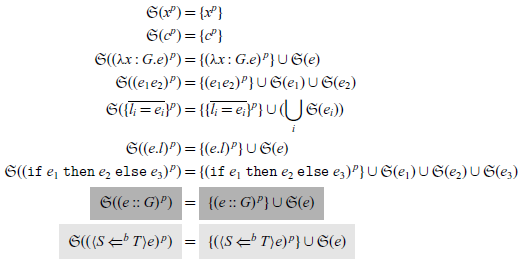
The light-gray highlighted part belongs to
![]() $\lambda_B$
, and the gray highlighted part belongs to
$\lambda_B$
, and the gray highlighted part belongs to
![]() $\lambda_\star$
. Other parts are common.
$\lambda_\star$
. Other parts are common.
Definition 2.4. (
![]() $m_{\mathfrak{S}(e)}$
.) Let
$m_{\mathfrak{S}(e)}$
.) Let
![]() $m_{\mathfrak{S}(e)}$
denote the multiplicity function of
$m_{\mathfrak{S}(e)}$
denote the multiplicity function of
![]() $\mathfrak{S}(e)$
that maps every expression to the number of its occurrence in
$\mathfrak{S}(e)$
that maps every expression to the number of its occurrence in
![]() $\mathfrak{S}(e)$
.
$\mathfrak{S}(e)$
.
Definition 2.5 (expression occurring in e). We say an expression e’ occurs in e if
![]() $m_{\mathfrak{S}(e)}(e')>0$
.
$m_{\mathfrak{S}(e)}(e')>0$
.
Definition 2.6. (well-labeled). An expression e is well-labeled if:
1. for all e’ occurring in e,
 $m_{\mathfrak{S}(e)}(e')=1$
;
$m_{\mathfrak{S}(e)}(e')=1$
;2. for every context label p, there is at most one sub-expression e’ occurring in e with context label p, i.e., the cardinal of the set
 $\{e' \mathrm{occurring in \textit{e}} \mid e' = t^p \mathrm{ for some \textit{t}}\}$
is at most 1.
$\{e' \mathrm{occurring in \textit{e}} \mid e' = t^p \mathrm{ for some \textit{t}}\}$
is at most 1.
That is, there will not be two exactly the same sub-expressions in e. Every sub-expression has a unique program label attached to it.
Definition 2.7. (cast occurring in e) We say a type cast
![]() $\langle S \Leftarrow^b T\rangle$
occurs in e for e an expression in
$\langle S \Leftarrow^b T\rangle$
occurs in e for e an expression in
![]() $\lambda_B$
, if there is a sub-expression
$\lambda_B$
, if there is a sub-expression
![]() $(\langle S \Leftarrow^b T\rangle e')^{\,p}$
occurring in e. Similarly, we say that a type cast combination
$(\langle S \Leftarrow^b T\rangle e')^{\,p}$
occurring in e. Similarly, we say that a type cast combination
![]() $\langle T_1 \Leftarrow^{b_1} T_2 \Leftarrow^{b_2} T_3 ... T_n \Leftarrow^{b_n} T_{n+1} \rangle$
occurs in e if there is a sub-expression
$\langle T_1 \Leftarrow^{b_1} T_2 \Leftarrow^{b_2} T_3 ... T_n \Leftarrow^{b_n} T_{n+1} \rangle$
occurs in e if there is a sub-expression
![]() $(\langle T_1 \Leftarrow^{b_1} T_2 \Leftarrow^{b_2} T_3 ... T_n \Leftarrow^{b_n} T_{n+1} \rangle e')^{\,p}$
(where the omitted context labels are kept the same) occurring in e.
$(\langle T_1 \Leftarrow^{b_1} T_2 \Leftarrow^{b_2} T_3 ... T_n \Leftarrow^{b_n} T_{n+1} \rangle e')^{\,p}$
(where the omitted context labels are kept the same) occurring in e.
Definition 2.8. (occurring as an attached label; occurring as a blame label) We say a context label p occurs as an attached label in e, if there is a sub-expression
![]() $t^p$
occurring in e. Similarly, we say p occurs as a blame label in e, if there is a sub-expression
$t^p$
occurring in e. Similarly, we say p occurs as a blame label in e, if there is a sub-expression
![]() $(\langle S \Leftarrow^b T\rangle e')^{\,p'}$
occurring in e satisfying
$(\langle S \Leftarrow^b T\rangle e')^{\,p'}$
occurring in e satisfying
![]() $b=p$
.
$b=p$
.
Now we can formally assert that our representation of blame label is appropriate.
Proposition 2.9. Suppose that
![]() $\Gamma \vdash e \rightsquigarrow s : G$
where e is a well-labeled expression in
$\Gamma \vdash e \rightsquigarrow s : G$
where e is a well-labeled expression in
![]() $\lambda_\star$
, s is also well-labeled, and for every blame label b there is at most one type cast expression occurring in e with blame label b, i.e., the cardinal of set
$\lambda_\star$
, s is also well-labeled, and for every blame label b there is at most one type cast expression occurring in e with blame label b, i.e., the cardinal of set
![]() $\{e' \mathrm{occurring in \textit{e}} \mid e' = (\langle S \Leftarrow^b T\rangle e'')^{\,p}) \mathrm{ for some} $
S,T,e”
$\{e' \mathrm{occurring in \textit{e}} \mid e' = (\langle S \Leftarrow^b T\rangle e'')^{\,p}) \mathrm{ for some} $
S,T,e”
![]() $\}$
is at most 1.
$\}$
is at most 1.
Well-labeled is just an auxiliary definition to formalize the assumption that every sub-expression has a unique label attached to it.
Proof It is sufficient to show that, in each step of the translation process, newly inserted casts will use fresh blame labels. By an easy induction, we will show that, for every program e, if
![]() $\Gamma \vdash e \rightsquigarrow t^p : G$
, then p does not occur as a blame label in t. That is, the out-most attached context label p will never be used as a blame label inside t.
$\Gamma \vdash e \rightsquigarrow t^p : G$
, then p does not occur as a blame label in t. That is, the out-most attached context label p will never be used as a blame label inside t.
The proposition we need to prove is a direct corollary. Indeed, in the translation process defined in Figure 2, the newly generated blame labels are always the out-most attached context labels of the (translation result of) direct sub-terms. Since these context labels do not occur as blame labels in these direct sub-terms, the generated blame labels are therefore fresh.
Recall that every context label p occurs at most once in e. Moreover, we give two trivial observations about
![]() $\Gamma \vdash e \rightsquigarrow t^p : G$
without proof: (1) p must occur in e as an attached label (2) if a cast
$\Gamma \vdash e \rightsquigarrow t^p : G$
without proof: (1) p must occur in e as an attached label (2) if a cast
![]() $\langle S \Leftarrow^{\,p'} T \rangle$
occurs in t, then p’ must occur in e as an attached label.
$\langle S \Leftarrow^{\,p'} T \rangle$
occurs in t, then p’ must occur in e as an attached label.
Induction on
![]() $\Gamma \vdash e \rightsquigarrow t^p$
. Case T_Var and Case T_Con are direct.
$\Gamma \vdash e \rightsquigarrow t^p$
. Case T_Var and Case T_Con are direct.
Case T_Ann:
![]() $\Gamma \vdash e \rightsquigarrow t^{\,p_1} :T$
and
$\Gamma \vdash e \rightsquigarrow t^{\,p_1} :T$
and
![]() $\Gamma \vdash (e :: G)^{\,p_2} \rightsquigarrow (\langle G \Leftarrow^{\,p_1} T \rangle t^{\,p_1})^{\,p_2}$
. From the induction hypothesis and our observation, there is no cast with blame label
$\Gamma \vdash (e :: G)^{\,p_2} \rightsquigarrow (\langle G \Leftarrow^{\,p_1} T \rangle t^{\,p_1})^{\,p_2}$
. From the induction hypothesis and our observation, there is no cast with blame label
![]() $p_1$
or
$p_1$
or
![]() $p_2$
occurs in t, thus the conclusion holds for
$p_2$
occurs in t, thus the conclusion holds for
![]() $(\langle G \Leftarrow^{\,p_1} T \rangle t^{\,p_1})^{\,p_2}$
.
$(\langle G \Leftarrow^{\,p_1} T \rangle t^{\,p_1})^{\,p_2}$
.
Case T_Lam:
![]() $\Gamma, (x:G) \vdash e \rightsquigarrow s :T$
and
$\Gamma, (x:G) \vdash e \rightsquigarrow s :T$
and
![]() $\Gamma \vdash (\lambda x:G.e)^{\,p} \rightsquigarrow (\lambda x:G.s)^{\,p} : G \to T$
. From our observation, p does not occur as a blame label in s. Apply the induction hypothesis, we know that every p occurs in s as a blame label at most once. Then the conclusion holds for
$\Gamma \vdash (\lambda x:G.e)^{\,p} \rightsquigarrow (\lambda x:G.s)^{\,p} : G \to T$
. From our observation, p does not occur as a blame label in s. Apply the induction hypothesis, we know that every p occurs in s as a blame label at most once. Then the conclusion holds for
![]() $(\lambda x:G.s)^{\,p}$
.
$(\lambda x:G.s)^{\,p}$
.
Case T_AppDyn:
![]() $\Gamma \vdash e_1 \rightsquigarrow t_1^{\,p_1} : \star$
and
$\Gamma \vdash e_1 \rightsquigarrow t_1^{\,p_1} : \star$
and
![]() $\Gamma \vdash e_2 \rightsquigarrow t_2^{\,p_2} :G$
. The result is
$\Gamma \vdash e_2 \rightsquigarrow t_2^{\,p_2} :G$
. The result is
![]() $e = ((\langle \star \to \star \Leftarrow^{\,p_1} \star \rangle t_1^{\,p_1\blacktriangleleft} )^{\,p_1} (\langle \star \Leftarrow^{\,p_2} G \rangle t_2^{\,p_2\blacktriangleleft})^{\,p_2})^{\,p_3} $
. By the induction hypothesis and our observation, we know that
$e = ((\langle \star \to \star \Leftarrow^{\,p_1} \star \rangle t_1^{\,p_1\blacktriangleleft} )^{\,p_1} (\langle \star \Leftarrow^{\,p_2} G \rangle t_2^{\,p_2\blacktriangleleft})^{\,p_2})^{\,p_3} $
. By the induction hypothesis and our observation, we know that
![]() $p_1,p_2,p_3$
does not occur as a blame label in
$p_1,p_2,p_3$
does not occur as a blame label in
![]() $t_1$
, nor in
$t_1$
, nor in
![]() $t_2$
. Then the conclusion holds for e. Other cases are similar.
$t_2$
. Then the conclusion holds for e. Other cases are similar.
2.2 Semantics of
 $\lambda_B$
Lg
$\lambda_B$
Lg
The whole definition of
![]() $\lambda_B$
is given in Figure 3, extending the syntax in Figure 1. As an intermediate language of gradual languages, the type system and runtime semantics of
$\lambda_B$
is given in Figure 3, extending the syntax in Figure 1. As an intermediate language of gradual languages, the type system and runtime semantics of
![]() $\lambda_B$
are standard. We let u,v,w range over values, r over intermediate evaluation results, and E over evaluation contexts. A value expression
$\lambda_B$
are standard. We let u,v,w range over values, r over intermediate evaluation results, and E over evaluation contexts. A value expression
![]() $v^p$
is an expression whose inner term v is a value. A value v is either a constant, a variable, a function, a record where each field is a value expression, a cast between functions or records, or an injection into dynamic from a non-dynamic type. Note this definition of value admits unbounded accumulation of casts on values.
$v^p$
is an expression whose inner term v is a value. A value v is either a constant, a variable, a function, a record where each field is a value expression, a cast between functions or records, or an injection into dynamic from a non-dynamic type. Note this definition of value admits unbounded accumulation of casts on values.

Fig. 3. The language
![]() $\lambda_B.$
$\lambda_B.$
Since
![]() $\lambda_B$
is an extension of
$\lambda_B$
is an extension of
![]() $\lambda_\star$
, we reuse the relation
$\lambda_\star$
, we reuse the relation
![]() $\Gamma \vdash e : G$
to represent the type system of
$\Gamma \vdash e : G$
to represent the type system of
![]() $\lambda_B$
.
$\lambda_B$
.
![]() $\lambda_B$
is a statically typed language. For a program t in
$\lambda_B$
is a statically typed language. For a program t in
![]() $\lambda_\star$
, it is trivial that
$\lambda_\star$
, it is trivial that
![]() $\emptyset \vdash e \rightsquigarrow s : G$
implies
$\emptyset \vdash e \rightsquigarrow s : G$
implies
![]() $\emptyset \vdash s : G$
.
$\emptyset \vdash s : G$
.
We use a binary relation
![]() $e \longrightarrow r$
to indicate a single-step reduction from an expression e to a result r. We say an expression e is a
$e \longrightarrow r$
to indicate a single-step reduction from an expression e to a result r. We say an expression e is a
![]() $\longrightarrow$
-redex if there exists an r such that
$\longrightarrow$
-redex if there exists an r such that
![]() $e \longrightarrow r$
. The standard reduction relation
$e \longrightarrow r$
. The standard reduction relation
![]() $e \longmapsto r$
is a simple closure of
$e \longmapsto r$
is a simple closure of
![]() $\longrightarrow$
. By induction, if e can be decomposed to E[e’] as a combination of an evaluation context E and a
$\longrightarrow$
. By induction, if e can be decomposed to E[e’] as a combination of an evaluation context E and a
![]() $\longrightarrow$
-redex e’, then e can reduce in one step by reducing e’ in one step. We use
$\longrightarrow$
-redex e’, then e can reduce in one step by reducing e’ in one step. We use
![]() $e \longmapsto^* r$
to indicate zero or more steps of reduction.
$e \longmapsto^* r$
to indicate zero or more steps of reduction.
The reader can disregard the manipulation of context labels momentarily and observe that the definition of
![]() $e \longrightarrow r$
is straightforward. A detailed explanation of context label manipulation will will be provided later. We assume an interpreting function
$e \longrightarrow r$
is straightforward. A detailed explanation of context label manipulation will will be provided later. We assume an interpreting function
![]() $[\![ ]\!]$
which interprets a constant c with respect to ty(c). If ty(c) is a function type, we assume the return value of
$[\![ ]\!]$
which interprets a constant c with respect to ty(c). If ty(c) is a function type, we assume the return value of
![]() $[\![ c ]\!] $
is still a constant. For example,
$[\![ c ]\!] $
is still a constant. For example,
![]() $[\![ + ]\!] v$
is itself a constant which can be interpreted as a computable function that maps any integer n to the result of
$[\![ + ]\!] v$
is itself a constant which can be interpreted as a computable function that maps any integer n to the result of
![]() $v+n$
if v is an integer, and undefined otherwise. Rules for application, record projection, conditional expression, cast elimination, and cast decomposition are standard. Note that we also give a rule concerning record type besides function type. A cast between two record types is resolved into a less complicated cast between types of the fields being accessed.
$v+n$
if v is an integer, and undefined otherwise. Rules for application, record projection, conditional expression, cast elimination, and cast decomposition are standard. Note that we also give a rule concerning record type besides function type. A cast between two record types is resolved into a less complicated cast between types of the fields being accessed.
In Figure 3, blame is always assigned to the downcast. Therefore,
![]() $\lambda_B$
resembles the D strategy in Siek et al. (Reference Siek, Garcia and Taha2009). Static Blame is easy to migrate between different blame strategies by simply changing the process of flow analysis that will be introduced in Section 3 to match the runtime semantics.
$\lambda_B$
resembles the D strategy in Siek et al. (Reference Siek, Garcia and Taha2009). Static Blame is easy to migrate between different blame strategies by simply changing the process of flow analysis that will be introduced in Section 3 to match the runtime semantics.
Now we give a detailed explanation of context label manipulation in reduction. Note that context labels occurring in an expression do not affect its evaluation. The general design principle which we will prove later is that if
![]() $t_1^{\,p_1} \longmapsto t_2^{\,p_2}$
then
$t_1^{\,p_1} \longmapsto t_2^{\,p_2}$
then
![]() $p_1 = p_2$
. In other words, context label is a way to track evaluation steps similar to program labels in standard flow analysis. As a result,
$p_1 = p_2$
. In other words, context label is a way to track evaluation steps similar to program labels in standard flow analysis. As a result,
![]() $t[x := v]$
is still defined as a term substitution to preserve attached context labels. More specifically,
$t[x := v]$
is still defined as a term substitution to preserve attached context labels. More specifically,
![]() $x^p[x := v]=v^p$
.
$x^p[x := v]=v^p$
.
Additionally, context labels enable us to encode type cast, specifying both the source and the target. For a type cast expression
![]() $(\langle S \Leftarrow^b T \rangle t^{\,p_1})^{\,p_2}$
, we can interpret it not only as “the type of t is cast to S” but also as “the value of expression
$(\langle S \Leftarrow^b T \rangle t^{\,p_1})^{\,p_2}$
, we can interpret it not only as “the type of t is cast to S” but also as “the value of expression
![]() $p_1$
will become the value of expression
$p_1$
will become the value of expression
![]() $p_2$
through the cast
$p_2$
through the cast
![]() $\langle S \Leftarrow^b T \rangle$
”. By regarding type casts as a special form of value passing, it becomes possible to statically infer all possible combinations of type casts if one can obtain all flow information within the program. This is precisely the approach employed by Static Blame as formally demonstrated in Corollary 3.15.
$\langle S \Leftarrow^b T \rangle$
”. By regarding type casts as a special form of value passing, it becomes possible to statically infer all possible combinations of type casts if one can obtain all flow information within the program. This is precisely the approach employed by Static Blame as formally demonstrated in Corollary 3.15.
As in compilation relation, context refinement happens when cast expressions are generated. The refined context label p attached to an expression
![]() $t^p$
expresses which expression
$t^p$
expresses which expression
![]() $t^p$
will cast to. For example, in function cast decomposition,
$t^p$
will cast to. For example, in function cast decomposition,
the generated expression
![]() ${\color{red}(}\langle S_1 \Leftarrow^b T_1 \rangle w^{\,p_3} {\color{red})}^{\,p_1?}$
will be cast to the argument of the expression
${\color{red}(}\langle S_1 \Leftarrow^b T_1 \rangle w^{\,p_3} {\color{red})}^{\,p_1?}$
will be cast to the argument of the expression
![]() $v^{p_1}$
inside the left hand. Therefore, it has the refined context label
$v^{p_1}$
inside the left hand. Therefore, it has the refined context label
![]() $p_1?$
. Also, note that abandoning the context label
$p_1?$
. Also, note that abandoning the context label
![]() $p_2$
is acceptable in this reduction rule. First, considering that
$p_2$
is acceptable in this reduction rule. First, considering that
![]() $v^{p_1}$
is a value, we already know that the only possible value that will flow into
$v^{p_1}$
is a value, we already know that the only possible value that will flow into
![]() $p_2$
is exactly
$p_2$
is exactly
![]() $v^{p_1}$
. Second, the expression
$v^{p_1}$
. Second, the expression
![]() $p_2$
will be eliminated and disappear after reduction. Consequently, preserving the context label
$p_2$
will be eliminated and disappear after reduction. Consequently, preserving the context label
![]() $p_1$
is sufficient to maintain the necessary information for the remaining reduction steps.
$p_1$
is sufficient to maintain the necessary information for the remaining reduction steps.
Static Blame has four different kinds of context refinement
![]() $\epsilon$
, namely
$\epsilon$
, namely
![]() $\blacktriangleleft$
,
$\blacktriangleleft$
,
![]() $?$
,
$?$
,
![]() $!$
and l. All of them express a cast-to relation. In detail, an expression with context label
$!$
and l. All of them express a cast-to relation. In detail, an expression with context label
![]() $p\blacktriangleleft$
means that e will cast to an expression with context label p; an expression with context label
$p\blacktriangleleft$
means that e will cast to an expression with context label p; an expression with context label
![]() $p?$
(resp.
$p?$
(resp.
![]() $p!$
/pl) means that e will cast to a parameter (resp. a return value/an l field) of expressions with context label p. The concept context refinement is highly inspired by the concept “type kind” in Rastogi et al. (Reference Rastogi, Chaudhuri and Hosmer2012) and shares the same notation. It also has something in common with the concept “Tag” in Vitousek et al. (Reference Vitousek, Swords and Siek2017), and a more detailed discussion is listed in related work.
$p!$
/pl) means that e will cast to a parameter (resp. a return value/an l field) of expressions with context label p. The concept context refinement is highly inspired by the concept “type kind” in Rastogi et al. (Reference Rastogi, Chaudhuri and Hosmer2012) and shares the same notation. It also has something in common with the concept “Tag” in Vitousek et al. (Reference Vitousek, Swords and Siek2017), and a more detailed discussion is listed in related work.
We conclude this section with several formal properties of
![]() $\lambda_B$
.
$\lambda_B$
.
Lemma 2.10. Suppose that
![]() $t^{\,p}$
is an expression in
$t^{\,p}$
is an expression in
![]() $\lambda_B$
with
$\lambda_B$
with
![]() $\Gamma \vdash t^p : G$
, if
$\Gamma \vdash t^p : G$
, if
![]() $t^{\,p} \longmapsto^{*} (t^{\prime})^{\,p'}$
, then
$t^{\,p} \longmapsto^{*} (t^{\prime})^{\,p'}$
, then
![]() $p = p'$
.
$p = p'$
.
Proof It is sufficient to consider the single-step case
![]() $t^{\,p} \longmapsto (t^{\prime})^{\,p'}$
. Suppose that
$t^{\,p} \longmapsto (t^{\prime})^{\,p'}$
. Suppose that
![]() $t^{\,p} = E[t_1^{\,p_1}],(t^{\prime})^{\,p'} = E[t_2^{\,p_2}]$
and
$t^{\,p} = E[t_1^{\,p_1}],(t^{\prime})^{\,p'} = E[t_2^{\,p_2}]$
and
![]() $t_1^{\,p_1} \longrightarrow t_2^{\,p_2}$
, the conclusion is trivial if E is not a hole, hence we can assume that
$t_1^{\,p_1} \longrightarrow t_2^{\,p_2}$
, the conclusion is trivial if E is not a hole, hence we can assume that
![]() $t^{\,p} \longrightarrow (t^{\prime})^{\,p'}$
, but the conclusion is also immediate from the definition of
$t^{\,p} \longrightarrow (t^{\prime})^{\,p'}$
, but the conclusion is also immediate from the definition of
![]() $e \longrightarrow r$
.
$e \longrightarrow r$
.
The determinism of our semantics is ensured by the unique decomposition theorem.
Theorem 2.11 (Unique Decomposition.) For a well-typed closed expression e in
![]() $\lambda_B$
, either e is a value expression, or there exists an unique decomposition
$\lambda_B$
, either e is a value expression, or there exists an unique decomposition
![]() $e=E[s]$
, where s is a
$e=E[s]$
, where s is a
![]() $\longrightarrow$
-redex.
$\longrightarrow$
-redex.
The type safety property consists of a progress lemma and a preservation lemma. The progress lemma is a corollary of the unique decomposition theorem.
Theorem 2.12 (Type Safety.) For blame calculus
![]() $\lambda_B$
, we have:
$\lambda_B$
, we have:
1. (Preservation) For a
 $\lambda_B$
expression e, if
$\lambda_B$
expression e, if
 $\Gamma \vdash e:G$
and
$\Gamma \vdash e:G$
and
 $e \longmapsto s$
, then
$e \longmapsto s$
, then
 $\Gamma \vdash s : G$
.
$\Gamma \vdash s : G$
.2. (Progress) For a
 $\lambda_B$
expression e, if
$\lambda_B$
expression e, if
 $\emptyset \vdash e:G$
, then one of the following is true:
$\emptyset \vdash e:G$
, then one of the following is true:-
a. there exists an s such that
 $e \longmapsto s$
,
$e \longmapsto s$
, b. e is a value expression
 $v^p$
,
$v^p$
,c. there exists a blame label b such that
 .
.
-
3 The Static Blame framework
In this section, we introduce the formal definition of the Static Blame framework.
3.1 Labeled type and type flow
Recall that the main purpose of the Static Blame framework is to exploit data flows and develop a correspondence between static constraints and runtime behavior. The Static Blame framework achieves its goal with the concept of type flow which corresponds straightforwardly to type cast, and the type flow analysis which computes type flows statically.
The syntax of labeled type and type flow is given in Figure 4. Type flow consists of labeled types. As we explained in Section 1.3, a labeled type is an identifier used for tracking expression evaluation as program labels in standard flow analysis. Formally, a labeled type
![]() $\hat{G}$
is just a pair
$\hat{G}$
is just a pair
![]() $\langle G,p \rangle$
of a gradual type G and a context label p. By intuition, the labeled type represents an expression
$\langle G,p \rangle$
of a gradual type G and a context label p. By intuition, the labeled type represents an expression
![]() $t^p$
in
$t^p$
in
![]() $\lambda_B$
with the same context label. The gradual type G is a design redundancy since
$\lambda_B$
with the same context label. The gradual type G is a design redundancy since
![]() $\lambda_B$
is a statically typed language. The type of an expression e will not change during evaluation by preservation property. This redundancy gives Static Blame a straightforward correspondence: for a cast expression
$\lambda_B$
is a statically typed language. The type of an expression e will not change during evaluation by preservation property. This redundancy gives Static Blame a straightforward correspondence: for a cast expression
![]() $(\langle S \Leftarrow^b T\rangle t^{\,p_1})^{\,p_2}$
, it corresponds to type flow
$(\langle S \Leftarrow^b T\rangle t^{\,p_1})^{\,p_2}$
, it corresponds to type flow
![]() $\hat{T} \triangleright_b \hat{S}$
where
$\hat{T} \triangleright_b \hat{S}$
where
![]() $\hat{T} = \langle T,p_1 \rangle$
and
$\hat{T} = \langle T,p_1 \rangle$
and
![]() $\hat{S} = \langle S,p_2 \rangle$
. Similarly, for a cast combination
$\hat{S} = \langle S,p_2 \rangle$
. Similarly, for a cast combination
![]() $(\langle T_{n+1} \Leftarrow^{b_n} T_n ... T_3 \Leftarrow^{b_2} T_2 \Leftarrow^{b_1} T_{1} \rangle t^{\,p_1})^{\,p_{n+1}}$
where the omitted context labels are
$(\langle T_{n+1} \Leftarrow^{b_n} T_n ... T_3 \Leftarrow^{b_2} T_2 \Leftarrow^{b_1} T_{1} \rangle t^{\,p_1})^{\,p_{n+1}}$
where the omitted context labels are
![]() $p_2...p_n$
, it corresponds to a type flow combination
$p_2...p_n$
, it corresponds to a type flow combination
![]() $\hat{T_1} \triangleright_{b_1} ... \triangleright_{b_n} \hat{T}_{n+1}$
where
$\hat{T_1} \triangleright_{b_1} ... \triangleright_{b_n} \hat{T}_{n+1}$
where
![]() $\hat{T_i} = \langle T_i, p_i \rangle$
. The notation
$\hat{T_i} = \langle T_i, p_i \rangle$
. The notation
![]() $\hat{T_1} \triangleright_{b_1} ... \triangleright_{b_n} \hat{T}_{n+1}$
is an abbreviation for a collection of type flows
$\hat{T_1} \triangleright_{b_1} ... \triangleright_{b_n} \hat{T}_{n+1}$
is an abbreviation for a collection of type flows
![]() $\hat{T_1} \triangleright_{b_1} \hat{T_2}, \hat{T_2} \triangleright_{b_2} ... \hat{T}_{n} \triangleright_{b_n} \hat{T}_{n+1}$
.
$\hat{T_1} \triangleright_{b_1} \hat{T_2}, \hat{T_2} \triangleright_{b_2} ... \hat{T}_{n} \triangleright_{b_n} \hat{T}_{n+1}$
.

Fig. 4. Syntax for labeled type and type flow.
Type flow is an instance of constraint in standard flow analysis. Static Blame views a cast expression as a special value passing monitored by the blame mechanism. By intuition, a type flow
![]() $\langle T,p_1 \rangle \triangleright_b \langle S,p_2 \rangle$
means that the value of expression
$\langle T,p_1 \rangle \triangleright_b \langle S,p_2 \rangle$
means that the value of expression
![]() $t_1^{\,p_1}$
will be passed into expression
$t_1^{\,p_1}$
will be passed into expression
![]() $t_2^{\,p_2}$
, and a blame may be assigned to b if cast fails. In contrast, the ordinary value passing and variable binding relations are not monitored by the blame mechanism and are denoted by the dummy kind d, which serves as a flag that is distinct from any blame label.
$t_2^{\,p_2}$
, and a blame may be assigned to b if cast fails. In contrast, the ordinary value passing and variable binding relations are not monitored by the blame mechanism and are denoted by the dummy kind d, which serves as a flag that is distinct from any blame label.
Definition 3.1 (dummy type flow). A dummy type flow is a type flow
![]() $\hat{T} \triangleright_\varsigma \hat{S}$
where
$\hat{T} \triangleright_\varsigma \hat{S}$
where
![]() $\varsigma = d$
.
$\varsigma = d$
.
The whole type flow generation process consists of a dummy type flow generation process and a direct conversion from type casts to non-dummy type flows. The definition of dummy type flow generation relation
![]() $\Gamma \vdash e : G \mid C$
is given in Figure 5, where e is an expression in
$\Gamma \vdash e : G \mid C$
is given in Figure 5, where e is an expression in
![]() $\lambda_B$
, G is a gradual type, and C is a set of dummy type flows. Most rules mirror the control flow constraint generation in standard flow analysis.
$\lambda_B$
, G is a gradual type, and C is a set of dummy type flows. Most rules mirror the control flow constraint generation in standard flow analysis.

Fig. 5. Dummy type flow generation for
![]() $\lambda_B.$
$\lambda_B.$
Note that
![]() $\Gamma \vdash e : G \mid C$
is a deterministic relation. The following proposition is trivial.
$\Gamma \vdash e : G \mid C$
is a deterministic relation. The following proposition is trivial.
Proposition 3.2. Suppose that e is an expression in
![]() $\lambda_B$
,
$\lambda_B$
,
![]() $\Gamma$
is a gradual type environment, and G is a gradual type, the following two statements are equivalent.
$\Gamma$
is a gradual type environment, and G is a gradual type, the following two statements are equivalent.
1. There exists a set C of dummy type flows such that
 $\Gamma \vdash e : G \mid C$
.
$\Gamma \vdash e : G \mid C$
.2.
 $\Gamma \vdash e : G$
.
$\Gamma \vdash e : G$
.
Moreover, if there exist
![]() $C_1$
and
$C_1$
and
![]() $C_2$
such that
$C_2$
such that
![]() $\Gamma \vdash e: G \mid C_1$
and
$\Gamma \vdash e: G \mid C_1$
and
![]() $\Gamma \vdash e: G \mid C_2$
hold together, then
$\Gamma \vdash e: G \mid C_2$
hold together, then
![]() $C_1=C_2$
.
$C_1=C_2$
.
The whole type flow generation process is formally defined as a function
![]() $\varphi$
.
$\varphi$
.
Definition 3.3 (
![]() $\varphi(\Gamma,e)$
). For an expression e and a type environment
$\varphi(\Gamma,e)$
). For an expression e and a type environment
![]() $\Gamma$
, suppose that there exists G,C such that
$\Gamma$
, suppose that there exists G,C such that
![]() $\Gamma \vdash e : G \mid C$
, we define the collection of generated type flows of e under
$\Gamma \vdash e : G \mid C$
, we define the collection of generated type flows of e under
![]() $\Gamma$
as
$\Gamma$
as
It is trivial from the Proposition 3.2 that
![]() $\varphi(\Gamma,e)$
is defined exactly if e is well-typed under
$\varphi(\Gamma,e)$
is defined exactly if e is well-typed under
![]() $\Gamma$
.
$\Gamma$
.
3.2 Type flow analysis
Type flow analysis is a constraint-solving process. This process is described by an inductive relation
![]() $C \vdash \hat T \triangleright_b \hat S \checkmark $
in Figure 6 where C is a set of type flow and
$C \vdash \hat T \triangleright_b \hat S \checkmark $
in Figure 6 where C is a set of type flow and
![]() $\hat T \triangleright_b \hat S$
is a type flow derived in type flow analysis. The main work of type flow analysis is to decompose type flows by type structure and to recover the data flows mediated via dynamic types. In principle, these rules model value passing and cast generation/elimination happen at runtime.
$\hat T \triangleright_b \hat S$
is a type flow derived in type flow analysis. The main work of type flow analysis is to decompose type flows by type structure and to recover the data flows mediated via dynamic types. In principle, these rules model value passing and cast generation/elimination happen at runtime.

Fig. 6. Type flow analysis.
Rule J_Base is the initial situation. Rules J_Fun and J_Rec decompose type flows according to type structures. For a type flow
![]() $\hat S_1 \to \hat T_2 \triangleright_b \hat{T}_1 \to \hat{S}_2$
, J_Fun generates type flows for function parameter and return value with respect to their variance. And for a type flow
$\hat S_1 \to \hat T_2 \triangleright_b \hat{T}_1 \to \hat{S}_2$
, J_Fun generates type flows for function parameter and return value with respect to their variance. And for a type flow
![]() $ \{ \overline{l_i: \hat G_i} \} \triangleright_b \{ \overline{l_j: \hat G_j} \}$
, J_Rec generates type flows for each field l that exists in both
$ \{ \overline{l_i: \hat G_i} \} \triangleright_b \{ \overline{l_j: \hat G_j} \}$
, J_Rec generates type flows for each field l that exists in both
![]() $\{ \overline{l_i: G_i} \} $
and
$\{ \overline{l_i: G_i} \} $
and
![]() $ \{ \overline{l_j: G_j} \}$
.
$ \{ \overline{l_j: G_j} \}$
.
Rules J_TransDyn and J_Trans resemble cast elimination at runtime. The notation
![]() $C \vdash \hat T \triangleright_{b_1} \hat G \triangleright_{b_2} \hat S \checkmark$
is an abbreviation for two hypotheses
$C \vdash \hat T \triangleright_{b_1} \hat G \triangleright_{b_2} \hat S \checkmark$
is an abbreviation for two hypotheses
![]() $C \vdash \hat T \triangleright_{b_1} \hat G \checkmark$
and
$C \vdash \hat T \triangleright_{b_1} \hat G \checkmark$
and
![]() $C \vdash \hat G \triangleright_{b_2} \hat S \checkmark$
. By intuition, if
$C \vdash \hat G \triangleright_{b_2} \hat S \checkmark$
. By intuition, if
![]() $\hat T_\star$
is an inflow of a dynamic type
$\hat T_\star$
is an inflow of a dynamic type
![]() $\langle \star, p \rangle$
while
$\langle \star, p \rangle$
while
![]() $\hat S$
is an outflow of
$\hat S$
is an outflow of
![]() $\langle \star, p \rangle$
, then there is a possible data flow from
$\langle \star, p \rangle$
, then there is a possible data flow from
![]() $\hat T$
to
$\hat T$
to
![]() $\hat S$
. Rule J_TransDyn preserves blame label
$\hat S$
. Rule J_TransDyn preserves blame label
![]() $b_1$
rather than
$b_1$
rather than
![]() $b_2$
in its conclusion to mirror the evaluation rules in Figure 3. This behavioral mirroring is the key to the correspondence between type flow and type cast proved in Proposition 3.13. If other blame strategies are used (Siek et al., Reference Siek, Garcia and Taha2009), the analysis rules should also be modified to maintain behavioral mirroring.
$b_2$
in its conclusion to mirror the evaluation rules in Figure 3. This behavioral mirroring is the key to the correspondence between type flow and type cast proved in Proposition 3.13. If other blame strategies are used (Siek et al., Reference Siek, Garcia and Taha2009), the analysis rules should also be modified to maintain behavioral mirroring.
Rule J_Dummy, on the other hand, expresses ordinary value passing and has nothing to do with the blame mechanism.
The careful reader may wonder why the relation
![]() $C \vdash \tau \checkmark$
has no type checks. Actually, there is no need. We say a type flow
$C \vdash \tau \checkmark$
has no type checks. Actually, there is no need. We say a type flow
![]() $\hat{T} \triangleright_\varsigma \hat{S}$
is well-formed if
$\hat{T} \triangleright_\varsigma \hat{S}$
is well-formed if
![]() $T <' S$
. Then we can prove the following proposition.
$T <' S$
. Then we can prove the following proposition.
Proposition 3.4. For an expression e and a type environment
![]() $\Gamma$
, suppose that e is well-typed under
$\Gamma$
, suppose that e is well-typed under
![]() $\Gamma$
so that
$\Gamma$
so that
![]() $\varphi(\Gamma,e)$
is well-defined, then every type flow
$\varphi(\Gamma,e)$
is well-defined, then every type flow
![]() $\tau \in \varphi(\Gamma,e)$
is well-formed. Moreover, if every type flow in C is well-formed, then
$\tau \in \varphi(\Gamma,e)$
is well-formed. Moreover, if every type flow in C is well-formed, then
![]() $C \vdash \tau \checkmark$
implies that
$C \vdash \tau \checkmark$
implies that
![]() $\tau$
is well-formed.
$\tau$
is well-formed.
Proof From the fact that e is well-typed under
![]() $\Gamma$
and
$\Gamma$
and
![]() $\Gamma \vdash e : G \mid C'$
only generates type flows between the same type, the first statement is direct. The second statement is a trivial induction on
$\Gamma \vdash e : G \mid C'$
only generates type flows between the same type, the first statement is direct. The second statement is a trivial induction on
![]() $C \vdash \tau \checkmark$
.
$C \vdash \tau \checkmark$
.
Now we state an algorithm to calculate
![]() $C\vdash \tau \checkmark$
.
$C\vdash \tau \checkmark$
.
Definition 3.5 (closure computation). Given C, enumerates every
![]() $\tau$
such that
$\tau$
such that
![]() $C \vdash \tau \checkmark$
. This computation proceeds in the following steps:
$C \vdash \tau \checkmark$
. This computation proceeds in the following steps:
1. Initially, apply rule J_Base until saturation.
2. Next, apply rules J_Dummy, J_TransDyn and J_Trans until saturation.
3. Next, apply rules J_Fun and J_Rec until saturation.
4. Finally, jump back to step (2), if there is no new type flow derived, the algorithm terminates.
As a standard least fixed point algorithm, the correctness of this algorithm is trivial if it terminates. And we give a termination proof.
Theorem 3.6 (Termination). The closure computation terminates if the input C is finite.
Proof The result is quite clear from the fact that labeled types are finite, and each labeled type has only finitely many sub-trees. More specifically, we can define
![]() $Sub(\hat{T})$
as sub-trees of
$Sub(\hat{T})$
as sub-trees of
![]() $\hat{T}$
inductively as
$\hat{T}$
inductively as
1.
 $Sub(\langle \iota,p \rangle) = \{ \langle \iota,p \rangle \}$
$Sub(\langle \iota,p \rangle) = \{ \langle \iota,p \rangle \}$
2.
 $Sub(\langle \star,p \rangle) = \{ \langle \star,p \rangle \}$
$Sub(\langle \star,p \rangle) = \{ \langle \star,p \rangle \}$
3.
 $Sub(\langle T \to S, p \rangle) = \{ \langle T \to S, p \rangle \} \cup Sub(\langle T,p?\rangle) \cup Sub(\langle S,p!\rangle)$
$Sub(\langle T \to S, p \rangle) = \{ \langle T \to S, p \rangle \} \cup Sub(\langle T,p?\rangle) \cup Sub(\langle S,p!\rangle)$
4.
 $Sub(\langle \{ \overline{l_i = G_i} \}, p \rangle)=\{ \langle \{ \overline{l_i = G_i} \}, p \rangle \} \cup (\bigcup_i Sub(\langle G_i,pl \rangle))$
$Sub(\langle \{ \overline{l_i = G_i} \}, p \rangle)=\{ \langle \{ \overline{l_i = G_i} \}, p \rangle \} \cup (\bigcup_i Sub(\langle G_i,pl \rangle))$
Let
![]() $\mathbb{S}$
be the set of all sub-trees of all labeled type occurs in C, every derived type flow must of the form
$\mathbb{S}$
be the set of all sub-trees of all labeled type occurs in C, every derived type flow must of the form
![]() $\hat{T} \triangleright_\varsigma \hat{S}$
, where
$\hat{T} \triangleright_\varsigma \hat{S}$
, where
![]() $\hat{T},\hat{S} \in \mathbb{S}$
, and
$\hat{T},\hat{S} \in \mathbb{S}$
, and
![]() $\varsigma$
is either a blame label b occurring in C or just the dummy flag. Since
$\varsigma$
is either a blame label b occurring in C or just the dummy flag. Since
![]() $\mathbb{S}$
and the set of blame labels occurring in C are both finite, the algorithm cannot proceed forever.
$\mathbb{S}$
and the set of blame labels occurring in C are both finite, the algorithm cannot proceed forever.
3.3 Type flow and type cast
In this section, we show that the type flow analysis on a
![]() $\lambda_B$
program e is an overapproximation. More specifically, we will prove that if e is well-typed, then type cast occurring in its evaluation can be derived by type flow analysis.
$\lambda_B$
program e is an overapproximation. More specifically, we will prove that if e is well-typed, then type cast occurring in its evaluation can be derived by type flow analysis.
First, we need some auxiliary definitions.
Definition 3.7 (trivial type flow). A dummy type flow
![]() $\tau = \hat{T} \triangleright_d \hat{S}$
is trivial if
$\tau = \hat{T} \triangleright_d \hat{S}$
is trivial if
![]() $\hat{T} = \hat{S}$
.
$\hat{T} = \hat{S}$
.
A trivial type flow is a dummy type flow with the same source and target.
Definition 3.8 (non-trivial type flow closure;
![]() $\overline{C}$
). Suppose that C is a set of type flows, then the non-trivial type flow closure of C, denoted by
$\overline{C}$
). Suppose that C is a set of type flows, then the non-trivial type flow closure of C, denoted by
![]() $\overline{C}$
, is defined as
$\overline{C}$
, is defined as
![]() $\overline{C} = \{\tau \mid C \vdash \tau \checkmark \wedge \tau \mathrm{ is not trivial}\} $
.
$\overline{C} = \{\tau \mid C \vdash \tau \checkmark \wedge \tau \mathrm{ is not trivial}\} $
.
We say that
![]() $\Gamma;e\vdash \tau \checkmark$
if
$\Gamma;e\vdash \tau \checkmark$
if
![]() $\varphi(\Gamma,e) \vdash \tau \checkmark$
.
$\varphi(\Gamma,e) \vdash \tau \checkmark$
.
Definition 3.9 (C dominates e under
![]() $\Gamma$
). Suppose that e is well-typed under
$\Gamma$
). Suppose that e is well-typed under
![]() $\Gamma$
so that
$\Gamma$
so that
![]() $\varphi(\Gamma,e)$
is defined, we say that a set of type flows C dominates e under
$\varphi(\Gamma,e)$
is defined, we say that a set of type flows C dominates e under
![]() $\Gamma$
, if for every non-trivial type flow such that
$\Gamma$
, if for every non-trivial type flow such that
![]() $\Gamma;e \vdash \tau \checkmark$
, we have
$\Gamma;e \vdash \tau \checkmark$
, we have
![]() $C \vdash \tau \checkmark$
. That is,
$C \vdash \tau \checkmark$
. That is,
![]() $\overline{\varphi(\Gamma,e)} \subseteq \overline{C}.$
$\overline{\varphi(\Gamma,e)} \subseteq \overline{C}.$
As a special case,
![]() $\varphi(\Gamma,e)$
itself dominates e under
$\varphi(\Gamma,e)$
itself dominates e under
![]() $\Gamma$
.
$\Gamma$
.
All induction proof about dominance relation requires the following lemma.
Lemma 3.10 (Inversion lemma on Domination). Suppose that C dominates e under
![]() $\Gamma$
:
$\Gamma$
:
1. if
 $e = (\langle S \Leftarrow^b T \rangle t^{\,p'})^{\,p}$
, then C also dominates
$e = (\langle S \Leftarrow^b T \rangle t^{\,p'})^{\,p}$
, then C also dominates
 $t^{\,p'}$
under
$t^{\,p'}$
under
 $\Gamma$
, moreover
$\Gamma$
, moreover
 $\tau \in \overline{C}$
where
$\tau \in \overline{C}$
where
 $\tau = \langle T,p' \rangle \triangleright_b \langle S,p \rangle$
;
$\tau = \langle T,p' \rangle \triangleright_b \langle S,p \rangle$
;2. if
 $e = (\lambda x:G.t^{\,p'})^{\,p} $
, then C also dominates
$e = (\lambda x:G.t^{\,p'})^{\,p} $
, then C also dominates
 $t^{\,p'}$
under
$t^{\,p'}$
under
 $\Gamma,x:G$
, moreover
$\Gamma,x:G$
, moreover
 ${\{ \overline{ \hat{G} \triangleright_{d} \hat{G_i} }, \hat{T'} \triangleright_{d} \hat{T}\}} \subseteq \overline{C}$
, where
${\{ \overline{ \hat{G} \triangleright_{d} \hat{G_i} }, \hat{T'} \triangleright_{d} \hat{T}\}} \subseteq \overline{C}$
, where
 $\hat{G},\hat{G_i},\hat{T'},\hat{T}$
have the same meaning as the premises of F_Lam ;
$\hat{G},\hat{G_i},\hat{T'},\hat{T}$
have the same meaning as the premises of F_Lam ;
3. if
 $e = (t_1^{\,p_1} t_2^{\,p_2})^{\,p_3} $
, then C also dominates both
$e = (t_1^{\,p_1} t_2^{\,p_2})^{\,p_3} $
, then C also dominates both
 $t_1^{\,p_1}$
and
$t_1^{\,p_1}$
and
 $t_2^{\,p_2}$
under
$t_2^{\,p_2}$
under
 $\Gamma$
, moreover
$\Gamma$
, moreover
 $\{ \hat{T_2} \triangleright_d \hat{T_1}, \hat{G} \triangleright_d \hat{G'}\} \subseteq \overline{C}$
, where
$\{ \hat{T_2} \triangleright_d \hat{T_1}, \hat{G} \triangleright_d \hat{G'}\} \subseteq \overline{C}$
, where
 $\hat{T_1},\hat{T_2},\hat{G},\hat{G'}$
have the same meaning as the premises of F_App ;
$\hat{T_1},\hat{T_2},\hat{G},\hat{G'}$
have the same meaning as the premises of F_App ;
4. if
 $e = \{\overline{l_i = t_i^{\,p_i}} \}^p$
where i ranges for
$e = \{\overline{l_i = t_i^{\,p_i}} \}^p$
where i ranges for
 $1,...,n$
, then C also dominates
$1,...,n$
, then C also dominates
 $t_i^{\,p_i}$
under
$t_i^{\,p_i}$
under
 $\Gamma$
for every
$\Gamma$
for every
 $i \in \{1,...,n \}$
, moreover
$i \in \{1,...,n \}$
, moreover
 $ \{\overline{\hat{G_i} \triangleright_d \hat{G_{li}}} \} \subseteq \overline{C}$
, where
$ \{\overline{\hat{G_i} \triangleright_d \hat{G_{li}}} \} \subseteq \overline{C}$
, where
 $\hat{G_i},\hat{G_{li}}$
have the same meaning as the premises of F_Rcd ;
$\hat{G_i},\hat{G_{li}}$
have the same meaning as the premises of F_Rcd ;
5. if
 $e = (t^{\,p_1}.l)^{\,p}$
, then C also dominates
$e = (t^{\,p_1}.l)^{\,p}$
, then C also dominates
 $t^{\,p_1}$
under
$t^{\,p_1}$
under
 $\Gamma$
, moreover
$\Gamma$
, moreover
 $\{\hat{G} \triangleright_d \hat{G'}\} \subseteq \overline{C}$
, where
$\{\hat{G} \triangleright_d \hat{G'}\} \subseteq \overline{C}$
, where
 $\hat{G},\hat{G'}$
have the same meaning as the premises of F_Proj;
$\hat{G},\hat{G'}$
have the same meaning as the premises of F_Proj;
6. if
 $e = ({\mathrm{\texttt{if}}}\ e_1\ {\mathrm{\texttt{then}}}\ e_2\ {\mathrm{\texttt{else}}}\ e_3)^{\,p_3}$
, then C also dominates
$e = ({\mathrm{\texttt{if}}}\ e_1\ {\mathrm{\texttt{then}}}\ e_2\ {\mathrm{\texttt{else}}}\ e_3)^{\,p_3}$
, then C also dominates
 $e_i$
under
$e_i$
under
 $\Gamma$
for
$\Gamma$
for
 $i \in \{1,2,3 \}$
, moreover
$i \in \{1,2,3 \}$
, moreover
 $\{ \hat{G_1} \triangleright_d \hat{G}, \hat{G_2} \triangleright_d \hat{G}\} \subseteq \overline{C}$
, where
$\{ \hat{G_1} \triangleright_d \hat{G}, \hat{G_2} \triangleright_d \hat{G}\} \subseteq \overline{C}$
, where
 $\hat{G_1},\hat{G_2},\hat{G}$
have the same meaning as the premises of F_If.
$\hat{G_1},\hat{G_2},\hat{G}$
have the same meaning as the premises of F_If.
Proof It is immediate from the definition of
![]() $\varphi$
function and domination.
$\varphi$
function and domination.
Now all we need to prove is that the dominance relation is preserved during evaluation.
Lemma 3.11 (Change of context label). Suppose that
![]() $\Gamma \vdash t^p : G$
, then for every set of type flows C dominating
$\Gamma \vdash t^p : G$
, then for every set of type flows C dominating
![]() $t^p$
under
$t^p$
under
![]() $\Gamma$
such that
$\Gamma$
such that
![]() $\langle G,p \rangle \triangleright_d \langle G,p' \rangle \in \overline{C}$
, C also dominates
$\langle G,p \rangle \triangleright_d \langle G,p' \rangle \in \overline{C}$
, C also dominates
![]() $t^{\,p'}$
under
$t^{\,p'}$
under
![]() $\Gamma$
.
$\Gamma$
.
Proof Induction on
![]() $\Gamma \vdash t^p : G$
. Note that
$\Gamma \vdash t^p : G$
. Note that
![]() $\langle G,p \rangle \triangleright_d \langle G,p' \rangle \in \overline{C}$
implies that
$\langle G,p \rangle \triangleright_d \langle G,p' \rangle \in \overline{C}$
implies that
![]() $p \not= p'$
. The case where
$p \not= p'$
. The case where
![]() $t = c,x$
is trivial.
$t = c,x$
is trivial.
Suppose that
![]() $t = \lambda x:G . (t^{\prime})^{\,p_1}$
,
$t = \lambda x:G . (t^{\prime})^{\,p_1}$
,
![]() $\Gamma \vdash t^p: G \to T$
,
$\Gamma \vdash t^p: G \to T$
,
![]() $\overline{\varphi(\Gamma,t^{\,p})} \subseteq \overline{C}$
and
$\overline{\varphi(\Gamma,t^{\,p})} \subseteq \overline{C}$
and
![]() $\langle G \to T, p \rangle \triangleright_d \langle G \to T, p'\rangle \in C$
, we will show that
$\langle G \to T, p \rangle \triangleright_d \langle G \to T, p'\rangle \in C$
, we will show that
![]() $\overline{\varphi(\Gamma,t^{\,p'})} \subseteq \overline{C}$
. Let
$\overline{\varphi(\Gamma,t^{\,p'})} \subseteq \overline{C}$
. Let
![]() $\{\overline{x^{\,p_i}}\} = FVO(e,x)$
,
$\{\overline{x^{\,p_i}}\} = FVO(e,x)$
,
![]() $ \overline{\hat{G_i} = \langle G,p_i \rangle}$
, and
$ \overline{\hat{G_i} = \langle G,p_i \rangle}$
, and
![]() $\hat{G} = \langle G, p?\rangle, \hat{G'} = \langle G,p'?\rangle, \hat{T} = \langle T, p! \rangle, \hat{T'} = \langle T, p'! \rangle, \hat{T_1} = \langle T, p_1\rangle$
, we know that
$\hat{G} = \langle G, p?\rangle, \hat{G'} = \langle G,p'?\rangle, \hat{T} = \langle T, p! \rangle, \hat{T'} = \langle T, p'! \rangle, \hat{T_1} = \langle T, p_1\rangle$
, we know that
![]() $\varphi(\Gamma,t^{\,p'}) \setminus \varphi(\Gamma,t^{\,p}) = \{ \overline{ \hat{G'} \triangleright_{d} \hat{G_i} }, \hat{T_1} \triangleright_{d} \hat{T'}\}$
, and
$\varphi(\Gamma,t^{\,p'}) \setminus \varphi(\Gamma,t^{\,p}) = \{ \overline{ \hat{G'} \triangleright_{d} \hat{G_i} }, \hat{T_1} \triangleright_{d} \hat{T'}\}$
, and
![]() $\{ \overline{ \hat{G} \triangleright_{d} \hat{G_i} }, \hat{T_1} \triangleright_{d} \hat{T}\} \subseteq \varphi(\Gamma,t^{\,p}) \subseteq \overline{C}$
. Since
$\{ \overline{ \hat{G} \triangleright_{d} \hat{G_i} }, \hat{T_1} \triangleright_{d} \hat{T}\} \subseteq \varphi(\Gamma,t^{\,p}) \subseteq \overline{C}$
. Since
![]() $\langle G \to T, p \rangle \triangleright_d \langle G \to T, p'\rangle \in C$
, we have that
$\langle G \to T, p \rangle \triangleright_d \langle G \to T, p'\rangle \in C$
, we have that
![]() $\hat{G'} \triangleright_d \hat{G}, \hat{T} \triangleright_d \hat{T'} \in \overline{C}$
by
$\hat{G'} \triangleright_d \hat{G}, \hat{T} \triangleright_d \hat{T'} \in \overline{C}$
by ![]() . Then by
. Then by ![]() ,
,
![]() $\{ \overline{ \hat{G'} \triangleright_{d} \hat{G_i} }, \hat{T_1} \triangleright_{d} \hat{T'}\} \in \overline{C}$
. So that
$\{ \overline{ \hat{G'} \triangleright_{d} \hat{G_i} }, \hat{T_1} \triangleright_{d} \hat{T'}\} \in \overline{C}$
. So that
![]() $\varphi(\Gamma, t^{\,p'}) \subseteq \overline{C}$
, and then
$\varphi(\Gamma, t^{\,p'}) \subseteq \overline{C}$
, and then
![]() $\overline{\varphi(\Gamma, t^{\,p'})} \subseteq \overline{C}$
.
$\overline{\varphi(\Gamma, t^{\,p'})} \subseteq \overline{C}$
.
The case where
![]() $t = \{\overline{l_i = t_i}\}, (t_1^{\,p_1} t_2^{\,p_2}) , (t^{\,p_1}.l)^{\,p_2}$
or
$t = \{\overline{l_i = t_i}\}, (t_1^{\,p_1} t_2^{\,p_2}) , (t^{\,p_1}.l)^{\,p_2}$
or
![]() $t =(\mathrm{\texttt{if}}\ e_1\ \mathrm{\texttt{ then}}\ t_2^{\,p_1}\ \mathrm{\texttt{else}}\ t_3^{\,p_2}) $
is similar to lambda case.
$t =(\mathrm{\texttt{if}}\ e_1\ \mathrm{\texttt{ then}}\ t_2^{\,p_1}\ \mathrm{\texttt{else}}\ t_3^{\,p_2}) $
is similar to lambda case.
Finally, suppose that
![]() $t = \langle S \Leftarrow^b T \rangle (t^{\prime})^{\,p_1}$
, then
$t = \langle S \Leftarrow^b T \rangle (t^{\prime})^{\,p_1}$
, then
![]() $\varphi(\Gamma,t^{\,p'}) \setminus \varphi(\Gamma,t^{\,p}) = \{ \langle T, p_1 \rangle \triangleright_b \langle S, p' \rangle \}$
. From the hypothesis we know that
$\varphi(\Gamma,t^{\,p'}) \setminus \varphi(\Gamma,t^{\,p}) = \{ \langle T, p_1 \rangle \triangleright_b \langle S, p' \rangle \}$
. From the hypothesis we know that
![]() $\langle S,p \rangle \triangleright_d \langle S, p' \rangle,\langle T, p_1 \rangle \triangleright_b \langle S, p \rangle \in C$
, then by
$\langle S,p \rangle \triangleright_d \langle S, p' \rangle,\langle T, p_1 \rangle \triangleright_b \langle S, p \rangle \in C$
, then by ![]() we know that
we know that
![]() $\langle T, p_1 \rangle \triangleright_b \langle S, p' \rangle \in \overline{C}$
, and the conclusion follows.
$\langle T, p_1 \rangle \triangleright_b \langle S, p' \rangle \in \overline{C}$
, and the conclusion follows.
Now we can show the dominance relation is preserved under substitution.
Lemma 3.12 (Substitution). Suppose that C is a set of type flows,
![]() $\Gamma,(x:G) \vdash t^{\,p}:T$
,
$\Gamma,(x:G) \vdash t^{\,p}:T$
,
![]() $\Gamma \vdash v^{p'}:G$
and x is not free in v, if
$\Gamma \vdash v^{p'}:G$
and x is not free in v, if
1. C dominates
 $t^{\,p}$
under
$t^{\,p}$
under
 $\Gamma,(x:G)$
,
$\Gamma,(x:G)$
,2. C dominates
 $v^{p'}$
under
$v^{p'}$
under
 $\Gamma$
,
$\Gamma$
,3. for every
 $x^{\,p_i} \in FVO(t^{\,p},x)$
,
$x^{\,p_i} \in FVO(t^{\,p},x)$
,
 $C \vdash \langle G, p' \rangle \triangleright_d \langle G,p_i \rangle \checkmark$
, then C dominates
$C \vdash \langle G, p' \rangle \triangleright_d \langle G,p_i \rangle \checkmark$
, then C dominates
 $(t[x := v])^{\,p}$
under
$(t[x := v])^{\,p}$
under
 $\Gamma$
.
$\Gamma$
.
Proof Using a simple but somewhat tedious induction, one can show that
Therefore we only need to show that for every
![]() $x^{\,p_i} \in FVO(t^p,x)$
,
$x^{\,p_i} \in FVO(t^p,x)$
,
![]() $\varphi(\Gamma,v^{p_i}) \subseteq \overline{C}$
. That is, C dominates
$\varphi(\Gamma,v^{p_i}) \subseteq \overline{C}$
. That is, C dominates
![]() $v^{p_i}$
under
$v^{p_i}$
under
![]() $\Gamma$
. Since C dominates
$\Gamma$
. Since C dominates
![]() $x^{\,p_i}$
under
$x^{\,p_i}$
under
![]() $\Gamma,(x:G)$
trivially, it follows from lemma 3.11 that C dominates
$\Gamma,(x:G)$
trivially, it follows from lemma 3.11 that C dominates
![]() $v^{p_i}$
under
$v^{p_i}$
under
![]() $\Gamma,(x:G)$
. Since x is not free in v,
$\Gamma,(x:G)$
. Since x is not free in v,
![]() $\varphi(\Gamma,v^{p_i}) = \varphi((\Gamma,(x:G)),v^{p_i})$
. Therefore, C also dominates
$\varphi(\Gamma,v^{p_i}) = \varphi((\Gamma,(x:G)),v^{p_i})$
. Therefore, C also dominates
![]() $v^{p_i}$
under
$v^{p_i}$
under
![]() $\Gamma$
.
$\Gamma$
.
With the substitution lemma, we can show the dominance relation is preserved under single-step reduction.
Proposition 3.13 (Dominance Preservation of Reduction). Suppose that
![]() $\Gamma \vdash e : G$
,
$\Gamma \vdash e : G$
,
![]() $e \longrightarrow s$
, so that
$e \longrightarrow s$
, so that
![]() $\Gamma \vdash s : G$
. If C dominates e under
$\Gamma \vdash s : G$
. If C dominates e under
![]() $\Gamma$
, then C also dominates s under
$\Gamma$
, then C also dominates s under
![]() $\Gamma$
.
$\Gamma$
.
Proof Case analysis on the definition of
![]() $e \longrightarrow s$
.
$e \longrightarrow s$
.
1.
 $(c^{\,p_1} v^{p_2})^{\,p} \longrightarrow ([\![ c ]\!] v)^{\,p}$
: The result is immediate.
$(c^{\,p_1} v^{p_2})^{\,p} \longrightarrow ([\![ c ]\!] v)^{\,p}$
: The result is immediate.2.
 $ ((\lambda x :G.t^{\,p_1})^{\,p_2} v^{p_3})^{\,p} \longrightarrow (t[x:= v])^{\,p}$
: Since C dominates e, then whether
$ ((\lambda x :G.t^{\,p_1})^{\,p_2} v^{p_3})^{\,p} \longrightarrow (t[x:= v])^{\,p}$
: Since C dominates e, then whether
 $p_3 = {p_2}?$
or not, there must be a dummy type flow from p to every variable x in t. More precisely, let
$p_3 = {p_2}?$
or not, there must be a dummy type flow from p to every variable x in t. More precisely, let
 $\Gamma \vdash (\lambda x:G. t^{\,p_1})^{\,p_2}: G \to T$
,
$\Gamma \vdash (\lambda x:G. t^{\,p_1})^{\,p_2}: G \to T$
,
 $\overline{(x_i)^{\,p_i}} \in FVO(t^{\,p_1})$
,
$\overline{(x_i)^{\,p_i}} \in FVO(t^{\,p_1})$
,
 $\hat{G} = \langle G, {p_2}? \rangle$
,
$\hat{G} = \langle G, {p_2}? \rangle$
,
 $\hat{G'} = \langle G, {p_3} \rangle$
and
$\hat{G'} = \langle G, {p_3} \rangle$
and
 $ \overline{\hat{G_i} = \langle G_i,{p_i} \rangle}$
. Then from dummy type flow collection, we must have
$ \overline{\hat{G_i} = \langle G_i,{p_i} \rangle}$
. Then from dummy type flow collection, we must have
 $ \overline{\hat{G'} \triangleright_d \hat{G_i} \in \overline{C}}$
. Then from substitution Lemma 3.12, C dominates
$ \overline{\hat{G'} \triangleright_d \hat{G_i} \in \overline{C}}$
. Then from substitution Lemma 3.12, C dominates
 $(t[x:=v])^{\,p_1}$
. From
$(t[x:=v])^{\,p_1}$
. From  and
and  ,
,
 $ \langle T, p_1 \rangle \triangleright_d \langle T, p_2! \rangle, \langle T, p_1 \rangle \triangleright_d \langle T, p_2! \rangle \in \overline{C} $
(if they are not trivial, of course, otherwise the conclusion will be trivial, too). Then by the Lemma 3.11, the conclusion follows.
$ \langle T, p_1 \rangle \triangleright_d \langle T, p_2! \rangle, \langle T, p_1 \rangle \triangleright_d \langle T, p_2! \rangle \in \overline{C} $
(if they are not trivial, of course, otherwise the conclusion will be trivial, too). Then by the Lemma 3.11, the conclusion follows.3.
 $(\{\overline{l_i=v_i^{\,p_i}},l=v^{p'}\}^{\,p''}.l)^{\,p} \longrightarrow v^p$
. Suppose that
$(\{\overline{l_i=v_i^{\,p_i}},l=v^{p'}\}^{\,p''}.l)^{\,p} \longrightarrow v^p$
. Suppose that
 $\Gamma \vdash v:T$
, without loss of generality, we can assume that p, p’,p” are distinct, then it is sufficient to show that
$\Gamma \vdash v:T$
, without loss of generality, we can assume that p, p’,p” are distinct, then it is sufficient to show that
 $C \vdash \langle T,p' \rangle \triangleright_d \langle T,p \rangle$
. But it is direct from
$C \vdash \langle T,p' \rangle \triangleright_d \langle T,p \rangle$
. But it is direct from  , F_Proj and J_Dummy.
, F_Proj and J_Dummy.4.
 $(\mathrm{\texttt{if}}\ \mathrm{\texttt{true}}^{\,p_1}\ \mathrm{\texttt{then}}\ t_1^{\,p_2} \ \mathrm{\texttt{else}}\ t_2^{\,p_3})^{\,p} \longrightarrow t_1^p$
or
$(\mathrm{\texttt{if}}\ \mathrm{\texttt{true}}^{\,p_1}\ \mathrm{\texttt{then}}\ t_1^{\,p_2} \ \mathrm{\texttt{else}}\ t_2^{\,p_3})^{\,p} \longrightarrow t_1^p$
or
 $(\mathrm{\texttt{if}}\ \mathrm{\texttt{false}}^{\,p_1}\ \mathrm{\texttt{then}}\ t_1^{\,p_2} \ \mathrm{\texttt{else}}\ t_2^{\,p_3})^{\,p} \longrightarrow t_2^p$
: Suppose that
$(\mathrm{\texttt{if}}\ \mathrm{\texttt{false}}^{\,p_1}\ \mathrm{\texttt{then}}\ t_1^{\,p_2} \ \mathrm{\texttt{else}}\ t_2^{\,p_3})^{\,p} \longrightarrow t_2^p$
: Suppose that
 $\Gamma \vdash e:G$
, without loss of generality we can assume that
$\Gamma \vdash e:G$
, without loss of generality we can assume that
 $p_1 \not= p \not=p_2$
. It is sufficient to show that
$p_1 \not= p \not=p_2$
. It is sufficient to show that
 $\langle G_1, p_1 \rangle \triangleright_b \langle G, p \rangle, \langle G_1, p_1 \rangle \triangleright_b \langle G, p \rangle \in \overline{C}$
. And this is direct from
$\langle G_1, p_1 \rangle \triangleright_b \langle G, p \rangle, \langle G_1, p_1 \rangle \triangleright_b \langle G, p \rangle \in \overline{C}$
. And this is direct from  .
.5.
 $(\langle \iota \Leftarrow^{b} \iota \rangle \ c^{\,p_1})^{\,p} \longrightarrow c^p$
: trivial
$(\langle \iota \Leftarrow^{b} \iota \rangle \ c^{\,p_1})^{\,p} \longrightarrow c^p$
: trivial6.
 $(\langle \star \Leftarrow^{b_1} \star \Leftarrow^{b_2} G_\star\rangle \ v^{p'})^{\,p} \longrightarrow (\langle \star \Leftarrow^{b_2} G_\star\rangle v^{p'})^{\,p}$
: the conclusion follows from J_TransDyn.
$(\langle \star \Leftarrow^{b_1} \star \Leftarrow^{b_2} G_\star\rangle \ v^{p'})^{\,p} \longrightarrow (\langle \star \Leftarrow^{b_2} G_\star\rangle v^{p'})^{\,p}$
: the conclusion follows from J_TransDyn.7.
 $(\langle S_\star \Leftarrow^{b_1} \star \Leftarrow^{b_2} T_\star\rangle v^{p'})^{\,p} \longrightarrow (\langle S_\star \Leftarrow^{b_1} T_\star \rangle v^{p'})^{\,p}$
: the conclusion follows from J_Trans.
$(\langle S_\star \Leftarrow^{b_1} \star \Leftarrow^{b_2} T_\star\rangle v^{p'})^{\,p} \longrightarrow (\langle S_\star \Leftarrow^{b_1} T_\star \rangle v^{p'})^{\,p}$
: the conclusion follows from J_Trans.8.
 ${\color{blue}(} {\color{cyan}(}\langle T_1\to S_2 \Leftarrow^b S_1 \to T_2 \rangle v^{p_1}{\color{cyan})}^{\,p_2} w^{\,p_3}{\color{blue})}^p \longrightarrow {\color{blue}(}\langle S_2 \Leftarrow^b T_2 \rangle {\color{orange}(}v^{p_1} {\color{red}(}\langle S_1 \Leftarrow^b T_1 \rangle w^{\,p_3} {\color{red})}^{\,p_1?}{\color{orange})}^{\,p_1!} {\color{blue})}^p$
: This is one of the two most complicated cases, suppose that C dominates the left-hand under
${\color{blue}(} {\color{cyan}(}\langle T_1\to S_2 \Leftarrow^b S_1 \to T_2 \rangle v^{p_1}{\color{cyan})}^{\,p_2} w^{\,p_3}{\color{blue})}^p \longrightarrow {\color{blue}(}\langle S_2 \Leftarrow^b T_2 \rangle {\color{orange}(}v^{p_1} {\color{red}(}\langle S_1 \Leftarrow^b T_1 \rangle w^{\,p_3} {\color{red})}^{\,p_1?}{\color{orange})}^{\,p_1!} {\color{blue})}^p$
: This is one of the two most complicated cases, suppose that C dominates the left-hand under
 $\Gamma$
, from the inversion lemma we know that C dominates
$\Gamma$
, from the inversion lemma we know that C dominates
 $v^{p_1}$
and
$v^{p_1}$
and
 $w^{\,p_3}$
under
$w^{\,p_3}$
under
 $\Gamma$
. However, except for type flows in
$\Gamma$
. However, except for type flows in
 $\varphi(\Gamma,v^{p_1})$
and
$\varphi(\Gamma,v^{p_1})$
and
 $\varphi(\Gamma,w^{\,p_3})$
, there are only two non-trivial type flows in
$\varphi(\Gamma,w^{\,p_3})$
, there are only two non-trivial type flows in
 $\varphi(\Gamma ,e')$
:
$\varphi(\Gamma ,e')$
:
 $\langle T_1,p_3 \rangle \triangleright_b \langle S_1,p_1? \rangle$
and
$\langle T_1,p_3 \rangle \triangleright_b \langle S_1,p_1? \rangle$
and
 $\langle T_2,p_1! \rangle \triangleright_b \langle S_2,p \rangle$
, where e’ is the right hand. Both of these can be generated from J_Fun and J_Dummy.
$\langle T_2,p_1! \rangle \triangleright_b \langle S_2,p \rangle$
, where e’ is the right hand. Both of these can be generated from J_Fun and J_Dummy.9.
 ${\color{blue}(}{\color{cyan}(}\langle \{\overline{l_i : G_i},l: G\} \Leftarrow^q \{\overline{l_j : G_j},l: T\}\rangle v^{p_1}{\color{cyan})}^{\,p_2}.l{\color{blue})}^p \longrightarrow {\color{blue}(}\langle G \Leftarrow^q T \rangle {\color{orange}(}v^{p_1}.l{\color{orange})}^{\,p_1l} {\color{blue})}^p$
. This case is similar to the last case.
${\color{blue}(}{\color{cyan}(}\langle \{\overline{l_i : G_i},l: G\} \Leftarrow^q \{\overline{l_j : G_j},l: T\}\rangle v^{p_1}{\color{cyan})}^{\,p_2}.l{\color{blue})}^p \longrightarrow {\color{blue}(}\langle G \Leftarrow^q T \rangle {\color{orange}(}v^{p_1}.l{\color{orange})}^{\,p_1l} {\color{blue})}^p$
. This case is similar to the last case.
Our main result is a direct extension.
Theorem 3.14 (Dominance Preservation of Evaluation). Suppose that
![]() $\Gamma \vdash e : G$
,
$\Gamma \vdash e : G$
,
![]() $e \longmapsto^* s$
, so that
$e \longmapsto^* s$
, so that
![]() $\Gamma \vdash s : G$
. If C dominates e under
$\Gamma \vdash s : G$
. If C dominates e under
![]() $\Gamma$
, then C also dominates s under
$\Gamma$
, then C also dominates s under
![]() $\Gamma$
.
$\Gamma$
.
Proof It is sufficient to show that, if
![]() $\Gamma \vdash E[e] : G$
,
$\Gamma \vdash E[e] : G$
,
![]() $e \longrightarrow s$
and C dominates E[e], then C also dominates E[s]. Induction on the structure of E. The case that
$e \longrightarrow s$
and C dominates E[e], then C also dominates E[s]. Induction on the structure of E. The case that
![]() $E= [ ]$
is exactly the Proposition 3.13.
$E= [ ]$
is exactly the Proposition 3.13.
Suppose that
![]() $E = (E_1 t)^{\,p}$
,
$E = (E_1 t)^{\,p}$
,
![]() $E[e] = (E_1[e] t)^{\,p}$
, and
$E[e] = (E_1[e] t)^{\,p}$
, and
![]() $e \longrightarrow s$
. From the inversion lemma, we know that C dominates
$e \longrightarrow s$
. From the inversion lemma, we know that C dominates
![]() $E_1[e]$
and t, and from the induction hypothesis we know that C dominates
$E_1[e]$
and t, and from the induction hypothesis we know that C dominates
![]() $E_1[s]$
. From F_App, the type preservation lemma and the Lemma 2.10, C also dominates
$E_1[s]$
. From F_App, the type preservation lemma and the Lemma 2.10, C also dominates
![]() $E[s] = (E_1[s] t)^{\,p}$
. The case that
$E[s] = (E_1[s] t)^{\,p}$
. The case that
![]() $E = v E_1$
is similar.
$E = v E_1$
is similar.
Suppose that
![]() $E = \{\overline{l_i= v_i^{\,p_i}},l_i= E_1,\overline{l_j= t_j^{\,p_j}}\}$
,
$E = \{\overline{l_i= v_i^{\,p_i}},l_i= E_1,\overline{l_j= t_j^{\,p_j}}\}$
,
![]() $E[e] = E_1[e] t$
, and
$E[e] = E_1[e] t$
, and
![]() $e \longrightarrow s$
. From the inversion lemma, we know that C dominates
$e \longrightarrow s$
. From the inversion lemma, we know that C dominates
![]() $E_1[e], \overline{v_i^{\,p_i}}, \overline{t_j^{\,p_j}}$
, and from induction hypothesis we know that C dominates
$E_1[e], \overline{v_i^{\,p_i}}, \overline{t_j^{\,p_j}}$
, and from induction hypothesis we know that C dominates
![]() $E_1[s]$
. From F_Rec, the type preservation lemma and the Lemma 2.10, C also dominates E[s].
$E_1[s]$
. From F_Rec, the type preservation lemma and the Lemma 2.10, C also dominates E[s].
The case that
![]() $E = (E_1.l)^{\,p}$
, or
$E = (E_1.l)^{\,p}$
, or
![]() $(\mathrm{\texttt{if}}\ E_1\ \mathrm{\texttt{then}}\ e_1 \ \mathrm{\texttt{else}}\ e_2)^{\,p}$
can be analyzed by the same routine.
$(\mathrm{\texttt{if}}\ E_1\ \mathrm{\texttt{then}}\ e_1 \ \mathrm{\texttt{else}}\ e_2)^{\,p}$
can be analyzed by the same routine.
Suppose that
![]() $E = (\langle S \Leftarrow^b T\rangle E_1)^{\,p}$
,
$E = (\langle S \Leftarrow^b T\rangle E_1)^{\,p}$
,
![]() $\Gamma \vdash E[e] : G$
,
$\Gamma \vdash E[e] : G$
,
![]() $e \longrightarrow s$
. This case is quite direct, since
$e \longrightarrow s$
. This case is quite direct, since
![]() $\varphi(\Gamma,E_1[s]) \setminus \varphi(\Gamma,E[s]) = \{ \langle T,p \rangle \triangleright_d \langle S,p' \rangle\}$
where p’ is the out-most context label of
$\varphi(\Gamma,E_1[s]) \setminus \varphi(\Gamma,E[s]) = \{ \langle T,p \rangle \triangleright_d \langle S,p' \rangle\}$
where p’ is the out-most context label of
![]() $E_1[s]$
. However, this type flow is contained in C from the hypothesis and the Lemma 2.10, so C also dominates E[s].
$E_1[s]$
. However, this type flow is contained in C from the hypothesis and the Lemma 2.10, so C also dominates E[s].
Now the following statement is trivial.
Corollary 3.15. Suppose that e is a well-typed expression in
![]() $\lambda_B$
under type environment
$\lambda_B$
under type environment
![]() $\Gamma$
and
$\Gamma$
and
![]() $e \longmapsto^* s$
, then for all sub-expression
$e \longmapsto^* s$
, then for all sub-expression
![]() $(\langle S \Leftarrow^b T \rangle t^{\,p_1})^{\,p_2}$
occurring in s, there exists a non-dummy type flow
$(\langle S \Leftarrow^b T \rangle t^{\,p_1})^{\,p_2}$
occurring in s, there exists a non-dummy type flow
![]() $\tau = \langle T,p_1 \rangle \triangleright_b \langle S,p_2 \rangle$
such that
$\tau = \langle T,p_1 \rangle \triangleright_b \langle S,p_2 \rangle$
such that
![]() $\Gamma;e \vdash \tau \checkmark$
holds.
$\Gamma;e \vdash \tau \checkmark$
holds.
4 Error classification
The application of the Static Blame framework is to reason about the runtime behavior of gradual typing programs by type flow analysis. Ideally, this consists of two steps: use type flows to get information about type casts and characterize the runtime behavior by type casts.
To demonstrate the effect of Static Blame, we use type flow to formalize the potential error classification discussed in Section 1.4 and prove some properties of each category formally. Recall that, we say that a potential error is detected in a program e if type flow analysis derive
![]() $\Gamma;e \vdash \hat{T} \triangleright_{b_2}\hat{\star} \triangleright_{b_1} \hat{S} \checkmark$
where
$\Gamma;e \vdash \hat{T} \triangleright_{b_2}\hat{\star} \triangleright_{b_1} \hat{S} \checkmark$
where
![]() $T \not <' S$
. For the convenience of discussion, we say that
$T \not <' S$
. For the convenience of discussion, we say that
![]() $\hat S$
is an inconsistent context of a value expression
$\hat S$
is an inconsistent context of a value expression
![]() $v^p$
, if
$v^p$
, if
![]() $v^p$
has type T but
$v^p$
has type T but
![]() $T \not <' S$
.
$T \not <' S$
.
As we mentioned, we define three different categories of potential errors.
Definition 4.1 (potential error). For e a program in
![]() $\lambda_\star$
, if
$\lambda_\star$
, if
![]() $\emptyset \vdash e \rightsquigarrow s : G$
, the potential errors are defined as follows:
$\emptyset \vdash e \rightsquigarrow s : G$
, the potential errors are defined as follows:
1. a type flow
 $\langle \star, p \rangle \triangleright_b \hat S$
is a normal potential error, if for some T such that
$\langle \star, p \rangle \triangleright_b \hat S$
is a normal potential error, if for some T such that
 $\Gamma;e \vdash \hat T \triangleright_{b'} \langle \star, p \rangle \triangleright_b \hat S$
, we have
$\Gamma;e \vdash \hat T \triangleright_{b'} \langle \star, p \rangle \triangleright_b \hat S$
, we have
 $T \not <' S$
,
$T \not <' S$
,2. a type flow
 $\langle \star, p \rangle \triangleright_b \hat S$
is a strict potential error, if it is a normal potential error, and for every
$\langle \star, p \rangle \triangleright_b \hat S$
is a strict potential error, if it is a normal potential error, and for every
 $\hat T_\star$
such that
$\hat T_\star$
such that
 $\Gamma;e \vdash \hat T_\star \triangleright_{b'} \langle \star, p \rangle \triangleright_b \hat S$
, we have
$\Gamma;e \vdash \hat T_\star \triangleright_{b'} \langle \star, p \rangle \triangleright_b \hat S$
, we have
 $T_\star \not <' S$
,
$T_\star \not <' S$
,3. a dynamic labeled type
 $\langle \star, p \rangle$
is wrong, if it has at least one non-dynamic inflow, and for every
$\langle \star, p \rangle$
is wrong, if it has at least one non-dynamic inflow, and for every
 $\hat T_\star,\hat S_\star$
such that
$\hat T_\star,\hat S_\star$
such that
 $\Gamma;e \vdash \hat T_\star \triangleright_{b'} \langle \star, p \rangle \triangleright_b \hat S_\star$
, we have
$\Gamma;e \vdash \hat T_\star \triangleright_{b'} \langle \star, p \rangle \triangleright_b \hat S_\star$
, we have
 $T_\star \not <' S_\star$
.
$T_\star \not <' S_\star$
.
Please note that a strict potential error is explicitly required to also be a normal potential error. This restriction prevents a situation where a type flow
![]() $\langle \star, p \rangle \triangleright_b \hat S$
is vacuously considered as a strict potential error when
$\langle \star, p \rangle \triangleright_b \hat S$
is vacuously considered as a strict potential error when
![]() $\langle \star, p \rangle$
has no inflow.
$\langle \star, p \rangle$
has no inflow.
We now discuss each category in turn.
4.1 Normal potential error: Complete
A normal potential error
![]() $\langle \star, p \rangle \triangleright_b \hat S$
indicates that a value may flow into an inconsistent context at runtime. Every type flow is monitored by a type cast with the same label, and type safety ensures that every dynamic type error should be caught by a runtime cast. Then a direct corollary of the correspondence is that every dynamic type error should be caught by a normal potential error statically.
$\langle \star, p \rangle \triangleright_b \hat S$
indicates that a value may flow into an inconsistent context at runtime. Every type flow is monitored by a type cast with the same label, and type safety ensures that every dynamic type error should be caught by a runtime cast. Then a direct corollary of the correspondence is that every dynamic type error should be caught by a normal potential error statically.
We can state this main property of potential type errors formally by blame label:
Theorem 4.2 (Completeness of normal potential error). For a program e’ in
![]() $\lambda_\star$
, if
$\lambda_\star$
, if
![]() $\Gamma \vdash e' \rightsquigarrow e$
, and
$\Gamma \vdash e' \rightsquigarrow e$
, and
![]() $e\longmapsto^* {\mathrm{\texttt{blame}}}\ b$
for some blame label b, then there is a normal potential error
$e\longmapsto^* {\mathrm{\texttt{blame}}}\ b$
for some blame label b, then there is a normal potential error
![]() $\langle \star, p \rangle \triangleright_b \hat S$
detected.
$\langle \star, p \rangle \triangleright_b \hat S$
detected.
Proof As
![]() $e\longmapsto^* {\mathrm{\texttt{blame}}}\ b$
, we have that
$e\longmapsto^* {\mathrm{\texttt{blame}}}\ b$
, we have that
![]() $e \longmapsto^* E[s]$
for some E and
$e \longmapsto^* E[s]$
for some E and
![]() $s = (\langle S_\star \Leftarrow^{b_1} \star \Leftarrow^{b_2} T_\star\rangle v^{p'})^{\,p}$
with
$s = (\langle S_\star \Leftarrow^{b_1} \star \Leftarrow^{b_2} T_\star\rangle v^{p'})^{\,p}$
with
![]() $T_{\star} \not <' S_{\star}$
. Apply the Corollary 3.15 and the result follows.
$T_{\star} \not <' S_{\star}$
. Apply the Corollary 3.15 and the result follows.
This theorem, as its name suggests, ensures that every possible blame error can be caught as a normal potential error. On the other hand, a program without any normal potential error will never trigger a blame error. Then the completeness of normal potential error ensures soundness of Static Blame as a software analysis technique.
However, completeness is not enough, we cannot claim that a program with detected normal type flow will necessarily trigger a runtime cast error. That is, detection for normal potential error is not sound. Even if we can assert that no normal potential error can be detected in a completely static program, it would still be a long way from soundness. That is the motivation for strict potential error.
4.2 Strict potential error: Sound up to erroneous casts
A type cast corresponding to a strict potential error is “definitely wrong”. For a strict potential error
![]() $\langle \star, p \rangle \triangleright_b \langle S, p_S\rangle$
, its definition requires every inflow of
$\langle \star, p \rangle \triangleright_b \langle S, p_S\rangle$
, its definition requires every inflow of
![]() $\langle \star, p \rangle$
to be inconsistent with S. Recall that in Section 2.1, we assume that ty(c) does not contain
$\langle \star, p \rangle$
to be inconsistent with S. Recall that in Section 2.1, we assume that ty(c) does not contain
![]() $\star$
for any constant c. Technically, this assumption serves as the proof for base case of the induction proof for Proposition 3.13. Essentially, it guarantees that constants of type
$\star$
for any constant c. Technically, this assumption serves as the proof for base case of the induction proof for Proposition 3.13. Essentially, it guarantees that constants of type
![]() $\star$
do not exist in our system. Therefore, if an expression
$\star$
do not exist in our system. Therefore, if an expression
![]() $t^p$
of type
$t^p$
of type
![]() $\star$
is evaluated to a value
$\star$
is evaluated to a value
![]() $v^p$
, v must be an upcast
$v^p$
, v must be an upcast
![]() $\langle \star \Leftarrow^{b'} G_\star \rangle (u)^{\,p'}$
. Then by Corollary 3.15, a type flow
$\langle \star \Leftarrow^{b'} G_\star \rangle (u)^{\,p'}$
. Then by Corollary 3.15, a type flow
![]() $\langle G_\star, p \rangle \triangleright_{b'} \langle \star, p \rangle$
can be deduced through type flow analysis. Since
$\langle G_\star, p \rangle \triangleright_{b'} \langle \star, p \rangle$
can be deduced through type flow analysis. Since
![]() $\langle \star, p \rangle \triangleright_b \hat S$
is a strict potential error, we can conclude that
$\langle \star, p \rangle \triangleright_b \hat S$
is a strict potential error, we can conclude that
![]() $G_\star \not <' S$
and the downcast expression
$G_\star \not <' S$
and the downcast expression
![]() $(\langle S \Leftarrow^{b} \star \rangle t^p)^{\,p_S}$
must fail, as it will be evaluated to
$(\langle S \Leftarrow^{b} \star \rangle t^p)^{\,p_S}$
must fail, as it will be evaluated to
![]() $(\langle S \Leftarrow^{b} \star \Leftarrow^{b'} G_\star \rangle (u)^{\,p'})^{\,p_S}$
.
$(\langle S \Leftarrow^{b} \star \Leftarrow^{b'} G_\star \rangle (u)^{\,p'})^{\,p_S}$
.
For real-world gradually typed language with constants of type dynamic (i.e., eval
Footnote 4
), further information is required to generate several extra inflow for each possible type of these constants (i.e., a type flow
![]() $\hat{\mathrm{\texttt{Int}}} \triangleright_b \hat{\star}$
for eval(“1")). Note that if we simply introduce inflows
$\hat{\mathrm{\texttt{Int}}} \triangleright_b \hat{\star}$
for eval(“1")). Note that if we simply introduce inflows
![]() $\hat{T} \triangleright_{b} \langle \star,p \rangle$
for each type T, it will prevent
$\hat{T} \triangleright_{b} \langle \star,p \rangle$
for each type T, it will prevent
![]() $\langle \star, p \rangle \triangleright_b \langle S, p_S\rangle$
from being a strict potential error since there will always exist a consistent inflow.
$\langle \star, p \rangle \triangleright_b \langle S, p_S\rangle$
from being a strict potential error since there will always exist a consistent inflow.
Strict potential errors describe a common mistake programmers make: an item of dynamic type is used incorrectly. It is hard to formally assert a cast is wrong, as we mentioned earlier in Section 1.4. Therefore, we formally define casts that never succeed as erroneous casts and claim that strict potential errors are sound with respect to erroneous casts. Formally, we define erroneous casts as follows:
Definition 4.3 (existence in the evaluation of e). Suppose that e is an expression in
![]() $\lambda_B$
and
$\lambda_B$
and
![]() $\Gamma \vdash e :G$
, we say a cast combination
$\Gamma \vdash e :G$
, we say a cast combination
![]() $(\langle T_1 \Leftarrow^{b_1} T_2 \Leftarrow^{b_2} T_3 ... T_n \Leftarrow^{b_n} T_{n+1} \rangle e' )^{\,p}$
exists in the evaluation of e if there exists s such that
$(\langle T_1 \Leftarrow^{b_1} T_2 \Leftarrow^{b_2} T_3 ... T_n \Leftarrow^{b_n} T_{n+1} \rangle e' )^{\,p}$
exists in the evaluation of e if there exists s such that
![]() $e \longmapsto^* s$
and
$e \longmapsto^* s$
and
![]() $(\langle T_1 \Leftarrow^{b_1} T_2 \Leftarrow^{b_2} T_3 ... T_n \Leftarrow^{b_n} T_{n+1} \rangle e' )^{\,p}$
(where the omitted context labels are kept the same) occurs in s.
$(\langle T_1 \Leftarrow^{b_1} T_2 \Leftarrow^{b_2} T_3 ... T_n \Leftarrow^{b_n} T_{n+1} \rangle e' )^{\,p}$
(where the omitted context labels are kept the same) occurs in s.
Definition 4.4 (erroneous sub-expression). For a program e in
![]() $\lambda_B$
, suppose
$\lambda_B$
, suppose
![]() $\Gamma \vdash e :G$
. We say a cast sub-expression
$\Gamma \vdash e :G$
. We say a cast sub-expression
![]() $(\langle S \Leftarrow^b \star \rangle t^{\,p_1})^{\,p_2}$
of e is erroneous in e, if for every cast combination
$(\langle S \Leftarrow^b \star \rangle t^{\,p_1})^{\,p_2}$
of e is erroneous in e, if for every cast combination
![]() $(\langle S \Leftarrow^b \star \Leftarrow^{b'} T_\star \rangle s)^{\,p_2}$
(the context label of inner cast expression is irrelevant) existing in the evaluation of e we have
$(\langle S \Leftarrow^b \star \Leftarrow^{b'} T_\star \rangle s)^{\,p_2}$
(the context label of inner cast expression is irrelevant) existing in the evaluation of e we have
![]() $T_\star \not <' S$
.
$T_\star \not <' S$
.
The definition is straightforward with respect to the semantics of
![]() $\lambda_B$
. If a dynamic down-cast
$\lambda_B$
. If a dynamic down-cast
![]() $\langle S \Leftarrow^b \star \rangle v$
happens, but the only possible value v is an up-cast
$\langle S \Leftarrow^b \star \rangle v$
happens, but the only possible value v is an up-cast
![]() $\langle \star \Leftarrow^{b'} T_\star \rangle v'$
from an inconsistent type, then the down-cast must fail after cast elimination.
$\langle \star \Leftarrow^{b'} T_\star \rangle v'$
from an inconsistent type, then the down-cast must fail after cast elimination.
Formally, erroneous casts are unsafe.
Definition 4.5 (unsafe cast expression). Suppose that e is an expression in
![]() $\lambda_B$
and
$\lambda_B$
and
![]() $\Gamma \vdash e :G$
, we say a cast expression
$\Gamma \vdash e :G$
, we say a cast expression
![]() $(\langle S \Leftarrow^b T \rangle e')^{\,p}$
is unsafe in e if, for every evaluation context E and expression
$(\langle S \Leftarrow^b T \rangle e')^{\,p}$
is unsafe in e if, for every evaluation context E and expression
![]() $s_1$
of form
$s_1$
of form
![]() $(\langle S \Leftarrow^b T \rangle s')^{\,p}$
,
$(\langle S \Leftarrow^b T \rangle s')^{\,p}$
,
![]() $e \longmapsto^\star E[s_1]$
implies either
$e \longmapsto^\star E[s_1]$
implies either
![]() $E[s_1] \longmapsto^* \mathrm{\texttt{blame}}\ b'$
for some b’ or e diverges.
$E[s_1] \longmapsto^* \mathrm{\texttt{blame}}\ b'$
for some b’ or e diverges.
Note that e’ may differ from s’, since e’ may change before cast elimination. To see this, consider the expression
![]() $(\lambda x:\star. (\langle Int \Leftarrow^b \star \rangle x)^{\,p}) (\langle \star \Leftarrow^{b'} \mathrm{\texttt{Bool}} \rangle \mathrm{\texttt{False}})$
where most irrelevant context labels omitted. Because the whole expression will reduce to
$(\lambda x:\star. (\langle Int \Leftarrow^b \star \rangle x)^{\,p}) (\langle \star \Leftarrow^{b'} \mathrm{\texttt{Bool}} \rangle \mathrm{\texttt{False}})$
where most irrelevant context labels omitted. Because the whole expression will reduce to
![]() $(\langle Int \Leftarrow^b \star \Leftarrow^{b'} \mathrm{\texttt{Bool}} \rangle \mathrm{\texttt{False}})^{\,p}$
and then abort with a blame message, the sub-expression
$(\langle Int \Leftarrow^b \star \Leftarrow^{b'} \mathrm{\texttt{Bool}} \rangle \mathrm{\texttt{False}})^{\,p}$
and then abort with a blame message, the sub-expression
![]() $(\langle Int \Leftarrow^b \star \rangle x)^{\,p} $
is unsafe but different from
$(\langle Int \Leftarrow^b \star \rangle x)^{\,p} $
is unsafe but different from
![]() $(\langle Int \Leftarrow^b \star \Leftarrow^{b'} \mathrm{\texttt{Bool}} \rangle \mathrm{\texttt{False}})^{\,p}$
.
$(\langle Int \Leftarrow^b \star \Leftarrow^{b'} \mathrm{\texttt{Bool}} \rangle \mathrm{\texttt{False}})^{\,p}$
.
Theorem 4.6 Every erroneous cast in e is unsafe in e.
Proof Suppose that
![]() $\Gamma \vdash e : G$
and
$\Gamma \vdash e : G$
and
![]() $T = \star$
, and the erroneous cast is
$T = \star$
, and the erroneous cast is
![]() $(\langle S \Leftarrow^b \star \rangle e')^{\,p}$
. Suppose that
$(\langle S \Leftarrow^b \star \rangle e')^{\,p}$
. Suppose that
![]() $e \longmapsto^* E[s_1]$
where
$e \longmapsto^* E[s_1]$
where
![]() $s_1$
is of the form
$s_1$
is of the form
![]() $(\langle S \Leftarrow^b \star \rangle s')^{\,p}$
. Apply unique decomposition theorem on s’, either it is a value of dynamic type
$(\langle S \Leftarrow^b \star \rangle s')^{\,p}$
. Apply unique decomposition theorem on s’, either it is a value of dynamic type
![]() $(\langle \star \Leftarrow^{b'} T'\rangle {v'}^{\,p''})^{\,p'}$
where
$(\langle \star \Leftarrow^{b'} T'\rangle {v'}^{\,p''})^{\,p'}$
where
![]() $T' \not<' S$
and the conclusion follows, or it can continue to evaluate. The result of its evaluation is either a dynamically typed value, which is the same as in the first case, or it diverges, or it aborts with a blame message. All situations are trivial.
$T' \not<' S$
and the conclusion follows, or it can continue to evaluate. The result of its evaluation is either a dynamically typed value, which is the same as in the first case, or it diverges, or it aborts with a blame message. All situations are trivial.
Then we can formally state that every strict potential error detects an erroneous cast. That is, strict potential error detection is sound with respect to erroneous casts.
Theorem 4.7. Suppose that e is a well-typed expression in
![]() $\lambda_B$
, and
$\lambda_B$
, and
![]() $(\langle G \Leftarrow^b \star \rangle t^{\,p_1})^{\,p_2}$
occurs in e. If
$(\langle G \Leftarrow^b \star \rangle t^{\,p_1})^{\,p_2}$
occurs in e. If
![]() $\langle \star ,p_1 \rangle \triangleright_b \langle G,p_2 \rangle$
is a strict potential error in e, then
$\langle \star ,p_1 \rangle \triangleright_b \langle G,p_2 \rangle$
is a strict potential error in e, then
![]() $(\langle G \Leftarrow^b \star \rangle t^{\,p_1})^{\,p_2}$
is erroneous.
$(\langle G \Leftarrow^b \star \rangle t^{\,p_1})^{\,p_2}$
is erroneous.
Proof Suppose that the cast combination
![]() $(\langle G \Leftarrow^b \star \Leftarrow^{b'} T_\star \rangle s)^{\,p_2}$
exists in the evaluation of e (where the omitted context label is
$(\langle G \Leftarrow^b \star \Leftarrow^{b'} T_\star \rangle s)^{\,p_2}$
exists in the evaluation of e (where the omitted context label is
![]() $p_1$
), apply Corollary 3.15 twice, we know that
$p_1$
), apply Corollary 3.15 twice, we know that
![]() $\Gamma;e \vdash \langle T_\star,p \rangle \triangleright_{b'} \langle \star ,p_1 \rangle \checkmark$
and
$\Gamma;e \vdash \langle T_\star,p \rangle \triangleright_{b'} \langle \star ,p_1 \rangle \checkmark$
and
![]() $\Gamma;e \vdash \langle \star ,p_1 \rangle \triangleright_b \langle G,p_2 \rangle \checkmark$
for some p, since
$\Gamma;e \vdash \langle \star ,p_1 \rangle \triangleright_b \langle G,p_2 \rangle \checkmark$
for some p, since
![]() $\langle \star ,p_1 \rangle \triangleright_b \langle G,p_2 \rangle$
is a strict potential error, we have
$\langle \star ,p_1 \rangle \triangleright_b \langle G,p_2 \rangle$
is a strict potential error, we have
![]() $T_\star \not <' G$
.
$T_\star \not <' G$
.
4.3 Wrong dynamic types: Values that cannot be used
At last, a wrong dynamic type is a labeled type where every non-dynamic inflow is inconsistent with every non-dynamic outflow. By definition, it is equivalent to saying that every non-dynamic outflow
![]() $\langle \star, p \rangle \triangleright_b G_\star$
is a strict potential error. While a strict potential error means a value may be used in a wrong way, the value held in the wrong dynamic type
$\langle \star, p \rangle \triangleright_b G_\star$
is a strict potential error. While a strict potential error means a value may be used in a wrong way, the value held in the wrong dynamic type
![]() $\langle \star, p \rangle$
can never be used safely as any non-dynamic type. That is why a wrong dynamic type is more severe than a strict potential error.
$\langle \star, p \rangle$
can never be used safely as any non-dynamic type. That is why a wrong dynamic type is more severe than a strict potential error.
For example, consider a program:
where attached context labels are omitted. If we denote the contexts of parameter x and y by labels
![]() $p_1$
and
$p_1$
and
![]() $p_2$
in the compiled program, then type flow analysis will derive
$p_2$
in the compiled program, then type flow analysis will derive
![]() $ \mathrm{\texttt{Bool}} \triangleright_{b_1} \langle \star, p_1 \rangle \triangleright_{b_2} \langle \star, p_2 \rangle \triangleright_{b_3} \mathrm{\texttt{Int}}$
. Thus
$ \mathrm{\texttt{Bool}} \triangleright_{b_1} \langle \star, p_1 \rangle \triangleright_{b_2} \langle \star, p_2 \rangle \triangleright_{b_3} \mathrm{\texttt{Int}}$
. Thus
![]() $\langle \star, p_2 \rangle$
is a wrong dynamic type, while
$\langle \star, p_2 \rangle$
is a wrong dynamic type, while
![]() $\langle \star, p_1 \rangle$
is not. It may be somewhat counter-intuitive at first glance, as both
$\langle \star, p_1 \rangle$
is not. It may be somewhat counter-intuitive at first glance, as both
![]() $\langle \star, p_1 \rangle$
and
$\langle \star, p_1 \rangle$
and
![]() $\langle \star, p_2 \rangle$
hide the inconsistency between Int and Bool. The design principle of Static Blame is to statically assert properties about a gradually typed language with a given blame mechanism. The result of this program will be
$\langle \star, p_2 \rangle$
hide the inconsistency between Int and Bool. The design principle of Static Blame is to statically assert properties about a gradually typed language with a given blame mechanism. The result of this program will be
![]() $\mathrm{\texttt{blame}}\ b_3$
, that is, projection from
$\mathrm{\texttt{blame}}\ b_3$
, that is, projection from
![]() $\langle \star, p_2 \rangle$
to Int should be responsible for the dynamic consistency. Both
$\langle \star, p_2 \rangle$
to Int should be responsible for the dynamic consistency. Both
![]() $\langle \langle \star, p_1 \rangle \Leftarrow^{b_1} \mathrm{\texttt{Bool}} \rangle$
and
$\langle \langle \star, p_1 \rangle \Leftarrow^{b_1} \mathrm{\texttt{Bool}} \rangle$
and
![]() $\langle \langle \star, p_2 \rangle \Leftarrow^{b_2} \langle \star, p_1 \rangle \rangle$
are trivially legal, so
$\langle \langle \star, p_2 \rangle \Leftarrow^{b_2} \langle \star, p_1 \rangle \rangle$
are trivially legal, so
![]() $b_1$
and
$b_1$
and
![]() $b_2$
will not be blamed. Since the use of dynamic type value is denoted by a projection at run-time, we assume
$b_2$
will not be blamed. Since the use of dynamic type value is denoted by a projection at run-time, we assume
![]() $\langle \star, p_2 \rangle$
is wrong in keeping with the design principles of the blame mechanism. Formally, we can state the following property.
$\langle \star, p_2 \rangle$
is wrong in keeping with the design principles of the blame mechanism. Formally, we can state the following property.
Theorem 4.8. Suppose that e is an expression in
![]() $\lambda_B$
and
$\lambda_B$
and
![]() $\Gamma \vdash e :G$
, if
$\Gamma \vdash e :G$
, if
![]() $e \longmapsto^* E[(\langle G_\star \Leftarrow^b \star \rangle v^p)^{\,p'}]$
where
$e \longmapsto^* E[(\langle G_\star \Leftarrow^b \star \rangle v^p)^{\,p'}]$
where
![]() $\langle \star,p \rangle$
is a wrong dynamic type, then
$\langle \star,p \rangle$
is a wrong dynamic type, then
![]() $e \longmapsto^* {\mathrm{\texttt{blame}}}\ b$
.
$e \longmapsto^* {\mathrm{\texttt{blame}}}\ b$
.
Proof From the definition of value of dynamic type, we know that
![]() $v^p$
must be a cast expression. Since
$v^p$
must be a cast expression. Since
![]() $\langle \star,p \rangle$
is a wrong dynamic type,
$\langle \star,p \rangle$
is a wrong dynamic type,
![]() $v^p$
must be an erroneous cast. As a result of Theorem 4.6, the expression will abort with a blame message.
$v^p$
must be an erroneous cast. As a result of Theorem 4.6, the expression will abort with a blame message.
5 Evaluation
To evaluate the feasibility of Static Blame, we have implemented Static Blame as a bug detector on Grift Footnote 5 , called SLOG (Static Blame fOr Grift).
The experiments were conducted on a machine with an 8-core Footnote 6 Intel(R) Core(TM) i7-10700F CPU @ 2.90GHz processor with 16384 KB of cache and 16 GB of RAM running Arch Linux. The Grift compiler is version 0.1 Footnote 7 , and Racket is version v8.8 [cs].
5.1 Implementation
5.1.1 Static Blame for grift
Grift is a superset of
![]() $\lambda_\star$
discussed in this paper. It extends
$\lambda_\star$
discussed in this paper. It extends
![]() $\lambda_\star$
with several features. In our evaluation of the feasibility of Static Blame, we have selectively supported a significant portion of the commonly used features, including base types (Int, Float, Bool, Unit), operators on base types (e.g., fl+ for float addition.), binding structures (define, let, letrec), iterations (repeat), sequencing (begin), tuples (tuple), and reference types (box, vector) with guarded semantics. While most of these features can be implemented straightforwardly, reference types deserve additional discussion.
$\lambda_\star$
with several features. In our evaluation of the feasibility of Static Blame, we have selectively supported a significant portion of the commonly used features, including base types (Int, Float, Bool, Unit), operators on base types (e.g., fl+ for float addition.), binding structures (define, let, letrec), iterations (repeat), sequencing (begin), tuples (tuple), and reference types (box, vector) with guarded semantics. While most of these features can be implemented straightforwardly, reference types deserve additional discussion.
Guarded semantics is originally proposed by Herman et al. (Reference Herman, Tomb and Flanagan2010). With guarded semantics, each reference cell access (read and write) will be guarded by a cast between the expected type and the actual type of the reference cell. For example, let r be a reference value of type
![]() $\mathrm{\texttt{Ref}}\ \star$
, and i be a value of type Int. Then the cast term
$\mathrm{\texttt{Ref}}\ \star$
, and i be a value of type Int. Then the cast term
![]() $\langle \mathrm{\texttt{Ref}}\ \mathrm{\texttt{Int}} \Leftarrow^b \mathrm{\texttt{Ref}}\ \star \rangle r$
has type
$\langle \mathrm{\texttt{Ref}}\ \mathrm{\texttt{Int}} \Leftarrow^b \mathrm{\texttt{Ref}}\ \star \rangle r$
has type
![]() $\mathrm{\texttt{Ref}}\ \mathrm{\texttt{Int}}$
. With standard notation of reference types, dereference of this term will generate a downcast:
$\mathrm{\texttt{Ref}}\ \mathrm{\texttt{Int}}$
. With standard notation of reference types, dereference of this term will generate a downcast:
while assignments will generate an upcast:
Our implementation supports guarded reference semantics in a direct way. The content of a reference cell is denoted by a new context refinement
![]() $\odot$
. And flow analysis is extended by two new rules:
$\odot$
. And flow analysis is extended by two new rules:

Mutable vector type is supported in a similar manner, where every element of a vector is assumed to have the same labeled type.
5.1.2 Static blame implementation: SLOG
To evaluate the effectiveness of Static Blame, SLOG is implemented as a bug detector based on Static Blame. In this paper, we informally define a bug as a piece of code that does not work properly as the programmer intended. SLOG takes a Grift program as input, identifies three kinds of potential errors, and then generates bug reports.
First, SLOG maps each potential error to a bug. For each bug, SLOG generates a bug report that includes the bug itself and a collection of reasons for that specific bug. A reason for a bug represents a potential error that is mapped to that particular bug. It is important to note that a bug report may contain multiple reasons, as there can be multiple potential errors mapped to the same bug.
In our experiment, a bug is just a specific node of a syntax tree. In other words, a bug report produced by SLOG consists of (1) a node in the syntax tree of the input program and (2) a collection of potential errors. The mapping from a potential error to a specific node deserves some discussion.
Recall that, a normal (strict) potential error
![]() $\hat{T} \triangleright_b \hat{S} $
corresponds to a runtime type cast that may (must) fail with the blame label b. And if a type cast fails, the program will abort with a blame label indicating the syntax node where casts are located. Therefore, SLOG maps normal and strict potential errors into the syntax nodes indicated by their blame labels. Similarly, a wrong dynamic type is a labeled type
$\hat{T} \triangleright_b \hat{S} $
corresponds to a runtime type cast that may (must) fail with the blame label b. And if a type cast fails, the program will abort with a blame label indicating the syntax node where casts are located. Therefore, SLOG maps normal and strict potential errors into the syntax nodes indicated by their blame labels. Similarly, a wrong dynamic type is a labeled type
![]() $\langle \star,p \rangle$
, where p is a context label which also indicates a syntax node. SLOG maps wrong dynamic types into the syntax nodes indicated by their context labels.
$\langle \star,p \rangle$
, where p is a context label which also indicates a syntax node. SLOG maps wrong dynamic types into the syntax nodes indicated by their context labels.
Moreover, to compare the effectiveness of different categories of potential errors, SLOG can be restricted on a certain category of potential error. For example, when restricted to normal potential errors, SLOG will only map normal potential errors into bug reports. In other words, strict potential errors and wrong dynamic types are discarded. Note that restriction hardly affects the performance of SLOG, since the type flow analysis still needs to compute the entire closure.
5.2 Research questions
We evaluate the effectiveness and performance of SLOG. Specifically, we aim to answer the following two questions:
• RQ1 (Effectiveness): What is the effectiveness of SLOG? We plan to investigate whether SLOG can detect bugs from Grift programs, as well as the causes of false- positive reports and undetectable bugs.
• RQ2 (Performance): What is the performance of the Static Blame implementation? Specifically, we plan to investigate its correlation with program size and the proportion of typed code.
Replacing some annotations in a gradually typed program with dynamic types will get another gradually typed program, which is called a configuration of the original program. Therefore, a fully annotated gradually typed program with n type nodes has
![]() $2^n$
configurations. Note that, a single type annotation can have multiple type nodes. For example, a type annotation
$2^n$
configurations. Note that, a single type annotation can have multiple type nodes. For example, a type annotation
![]() $\mathrm{\texttt{Ref}}\ \mathrm{\texttt{Int}}$
can be “dynamized” into both
$\mathrm{\texttt{Ref}}\ \mathrm{\texttt{Int}}$
can be “dynamized” into both
![]() $\mathrm{\texttt{Ref}}\ \star$
and
$\mathrm{\texttt{Ref}}\ \star$
and
![]() $\star$
. Consequently, even a small program can have a huge space of configurations.
$\star$
. Consequently, even a small program can have a huge space of configurations.
Configurations are versions of the same program with different proportions of typed code. All configurations of a gradually typed program comprise the migratory lattice of this program. As Takikawa et al. (Reference Takikawa, Feltey, Greenman, New, Vitek and Felleisen2016) observes, the execution of a program may have an overhead of over 100
![]() $\times$
in the worst-case over the entire migratory lattice, much slower than both the fully static version and the fully dynamic version. This observation indicates that the proportion of typed code is a crucial metric for gradually typed programs. Consequently, conducting evaluations of SLOG with varying proportions of typed code is valuable. The evaluation of SLOG involves sampling across the lattice.
$\times$
in the worst-case over the entire migratory lattice, much slower than both the fully static version and the fully dynamic version. This observation indicates that the proportion of typed code is a crucial metric for gradually typed programs. Consequently, conducting evaluations of SLOG with varying proportions of typed code is valuable. The evaluation of SLOG involves sampling across the lattice.
5.3 Experimental setup
5.3.1 RQ1: Effectiveness
Ideally, SLOG should be evaluated on a representative collection of programs with runtime cast errors for RQ1. However, there is no such benchmark. Therefore, we take a similar approach to previous work about evaluating blame mechanism (Lazarek et al., Reference Lazarek, Greenman, Felleisen and Dimoulas2021), namely generating a corpus of errors by mutation analysis.
We say that a generated program is a legal scenario or simply scenario if it can be accepted by the Grift compiler. SLOG is evaluated on a collection of legal scenarios. Our approach proceeds as follows, and each step will be described in detail later.
1. Select a representative collection of static programs that: (1) make full use of the various features of the Grift language and (2) vary in size, complexity, and purpose.
2. Inject bugs into these programs with carefully designed mutators. The result programs are called mutants. A mutant is a legal scenario if it can be accepted by the compiler.
3. For each mutant, uniformly sample several programs from its migratory lattice, each sampling result that can be accepted by the compiler is also a legal scenario.
The starting program collection in our experiment is the original benchmark of Grift presented in Kuhlenschmidt et al. (Reference Kuhlenschmidt, Almahallawi and Siek2019). This benchmark consists of eight programs ported from other well-known benchmarks or textbook algorithms for Grift. We chose seven of them as the starting point of mutation analysis. The excluded program sieve uses recursive types not supported by our implementation. The sizes of these chosen programs range from 18 to 221 in terms of LOC, while the numbers of type nodes range from 8 to 280. Details are listed in Table 2.
Table 1. Summary of mutators

Table 2. Generated legal scenarios and metrics about source programs

Note: This table shows (1) the numbers of legal scenarios generated by each mutator and each source program after sampling from migratory lattices and (2) two metrics of each source program. The first four rows display legal scenarios, where each row represents a mutator and every column represents a source program. The number N in a cell (M,P) means that there are N legal scenarios in the set of (1) mutants generated by applying M to P along with (2) sampled programs from migratory lattices of these mutants. The last two rows provide two metrics. LOC refers to the Lines Of Code of each program, while NTN represents the Number of Type Nodes of each program.
The mutators we use are inherited from Lazarek et al. (Reference Lazarek, Greenman, Felleisen and Dimoulas2021) with slight changes. The mutators that can successfully generate legal scenarios are described in Table 1. Note that the arithmetic mutator is not a special case of the constant mutator, since operators in Grift are special forms, not constant values. We use only three mutators in the evaluation while Lazarek et al. (Reference Lazarek, Greenman, Felleisen and Dimoulas2021) describe 16 mutators. The main reason is that Lazarek et al. (Reference Lazarek, Greenman, Felleisen and Dimoulas2021) evaluate on the full-fledged language Racket (Flatt & PLT, Reference Flatt2010), while Grift has fewer features. As a result, mutators for some advanced language features are not portable to Grift. For example, Grift does not support classes, and mutators like swapping method identifiers are not portable.
Moreover, the mutators in Table 1 inject additional type ascriptions into programs, while their original version in Lazarek et al. (Reference Lazarek, Greenman, Felleisen and Dimoulas2021) does not. This is because Lazarek et al. (Reference Lazarek, Greenman, Felleisen and Dimoulas2021) processes coarse-grained gradual typing, which means they can hide injected bugs by making the module containing mutations untyped, while we process fine-grained gradual typing, and the injected bug can only be hidden by an explicit annotation. Note that the additional type ascription won’t change the number of configurations in its migratory lattice.
Migratory lattice represents type migration of gradually typed programs, which is the process of making a program more (resp. less) precise by changing the type annotation. Migration of gradually typed programs may change the runtime behavior of a gradually typed program. We also uniformly sample configurations from migratory lattices of mutants. The fully dynamic configuration and the fully static configuration are always chosen as special cases. We use the same sampling algorithm as Kuhlenschmidt et al. (Reference Kuhlenschmidt, Almahallawi and Siek2019) Footnote 8 . It takes a fully typed program, the number of samples, and the number of bins to be uniformly sampled as inputs. These bins partition the migratory lattice by dynamic annotation percentage of configurations in the lattice. And the algorithm will uniformly sample from each bin.
The generated legal scenarios after sampling are shown in Table 2. In summary, we sample 12 scenarios from the migratory lattice of each mutation, and we collect 16,464 legal scenarios by mutation analysis and sampling from migratory lattices.
Recall that a bug in a program is a specific node in the syntax tree of this program. We explicitly give an informal assumption to relate the concepts of bug, bug report, and mutation analysis. Under this assumption, each legal scenario has exactly one bug. We call it actual bug to distinguish it from the SLOG bug reports.
Assumption 1 We assume that every mutant has one bug where the mutation happens. We also assume that an actual bug can be located by a bug report if the report refers to a sub-tree of the actual bug.
Please note that the concept of sub-tree specifically relates to the structure of the Abstract Syntax Tree (AST) in the implementation of the Grift language. This concept is slightly different from sub-expressions formally defined in Definition 2.3. For example, in the case of the let binding
![]() $\mathrm{\texttt{let}}\ x\ =\ e_1\ \mathrm{\texttt{in}}\ e_2$
, the sub-tree
$\mathrm{\texttt{let}}\ x\ =\ e_1\ \mathrm{\texttt{in}}\ e_2$
, the sub-tree
![]() $x\ =\ e_1$
represents a binding AST node. However, since it is not a valid expression, it is not a sub-expression. In Section 5.5, we provide a discussion on the assumption concerning potential threats to validity.
$x\ =\ e_1$
represents a binding AST node. However, since it is not a valid expression, it is not a sub-expression. In Section 5.5, we provide a discussion on the assumption concerning potential threats to validity.
5.3.2 RQ2: Performance
For RQ2, we start by creating a collection of large programs called Size by repeating code in the ray program, which has the most type annotations. We make necessary renaming to avoid identifier conflict. The size of the programs in Size increases linearly, ranging from approximately 250 to 2500 lines of code (LOC). Next, we divide the migratory lattice of the ray program into ten bins based on the proportion of dynamic type annotations. Each bin covers a range from
![]() $10i\%$
to
$10i\%$
to
![]() $10(i + 1)\%$
, where i ranges from 0 to 9. From each bin, we randomly select 100 configurations, resulting in another collection of 1000 programs called Lattice.
$10(i + 1)\%$
, where i ranges from 0 to 9. From each bin, we randomly select 100 configurations, resulting in another collection of 1000 programs called Lattice.
5.4 Evaluation results and discussion
5.4.1 RQ1: Effectiveness
For RQ1, we run SLOG on every legal scenario and compare the reported bug location(s) with the actual bug location. More specifically, by Assumption 1, we say a bug report (i.e., one output of SLOG for a specific legal scenario) is a true positive if it refers to a sub-tree of the actual bug. For each legal scenario, we run SLOG three times, each time restricting SLOG to a different category of potential error. Therefore, there will be three categories of bug reports for each scenario.
The result of our evaluation is shown in Table 3. The precision is the rate of true positives in all bug reports. The recall is the rate of scenarios with any true positives among all scenarios. Intuitively, precision reflects how many reports are correct, while recall reflects how many actual bugs can be found by the SLOG. Overall, the relative relationship of precision rates is as we expected from the theory. Normal potential errors are the least precise, strict potential errors are more precise, and wrong dynamic types are the most precise. Accordingly, their recall rates also decrease in this order.
Table 3. Effectiveness evaluation of SLOG

NPE: Normal Potential Errors. SPE: Strict Potential Errors. WDT: Wrong Dynamic Types.
Note: This table shows the evaluation result in terms of the categories of our classification of errors. The column #Rep gives the number of bug reports among all legal scenarios. The column TP gives the number of true positives among these reports. The column #TSce gives the number of scenarios with any true positive reports. That is the number of detectable actual bugs. The precision is calculated by
![]() $\mathrm{TP}/\mathrm{\#Rep}$
, while the recall is the ratio of #TSce among all 16464 scenarios. Erecall is the recall of the dataset after removing non-type scenarios.
$\mathrm{TP}/\mathrm{\#Rep}$
, while the recall is the ratio of #TSce among all 16464 scenarios. Erecall is the recall of the dataset after removing non-type scenarios.
We delve into two issues: why SLOG detects false bugs and why certain bugs remain undetected. Therefore, we manually classify 1) the false-positive reports and 2) scenarios without any true-positive report. The theoretical nature of normal potential error, its similarity to strict potential error, and its low precision make it less interesting. Therefore, we only analyze strict potential error and wrong dynamic type.
Specifically, we manually classified all false-positive reports consisting of 1049 strict potential error reports and 655 wrong dynamic type reports. For scenarios without any true positive report, the classification procedure is conducted on two distinct samples.
The first sample comprises 371 scenarios without strict potential error reports, while the second sample comprises 372 scenarios without wrong dynamic type reports. Both samples exhibit a confidence level of 95% and a margin of error that does not exceed 5%. The sample size is calculated using calculator.net. The result of classification is listed in Table 4. We now explain each category in detail.
Table 4. Cause of false positives and false negatives

Note: This table shows our results of manual classification. Table Fp-cause shows the classification of false positive reports, while table NoTp-cause shows the classification of scenarios without true positive reports. That is the classification of reasons for undetectable bugs. Column SPE represents strict potential errors and WDT for wrong dynamic types.
The causes of false positives include Escape (ESC), Refinement (REF), and Implementation (IMP).
Escape (ESC) happens when a dynamically typed variable is assigned a value of a certain type but incorrectly used as another inconsistent type. For example, the following code assigns an integer to a variable x, and each use of x as an integer is an escape of strict potential errors.
If we view the syntax node
![]() $x\ :\ \star\ =\ 1.0$
as a bug (since replacing
$x\ :\ \star\ =\ 1.0$
as a bug (since replacing
![]() $1.0$
by 1 will fix it), then every cast inserted in the let-body that converts x from dynamic type to integer will result in a false positive of strict potential errors. Because the blame labels of these casts will refer to the use rather than the initial assignment
$1.0$
by 1 will fix it), then every cast inserted in the let-body that converts x from dynamic type to integer will result in a false positive of strict potential errors. Because the blame labels of these casts will refer to the use rather than the initial assignment
![]() $x\ :\ \star\ =\ 1.0$
.
$x\ :\ \star\ =\ 1.0$
.
This example does not result in false positives of wrong dynamic types since each use of x will have the same labeled type. However, when the value of x is assigned to another dynamically typed variable, the escape of wrong dynamic types also occurs.
In the Example 2, the dynamic type of y rather than x will be the wrong dynamic type reported since each use of y is an outflow of y rather than x. Similarly, if we still view the syntax node
![]() $x\ :\ \star\ =\ 1.0$
as a bug, a false positive occurs.
$x\ :\ \star\ =\ 1.0$
as a bug, a false positive occurs.
The Escape phenomenon exposes a fundamental limitation of Static Blame. In the absence of prior knowledge, distinguishing whether an assignment or use is a bug becomes challenging. For instance, in Example 2, it is unclear whether a floating-point variable is being improperly used as an integer variable or if a floating-point value is mistakenly passed into an integer variable. While escape problems can be solved simply by adding type annotations, they can also be addressed by tracking both the use and assignment without necessitating additional type annotations. Unfortunately, the current label tracking mechanism of Static Blame lacks this capability. As part of our future work, we aim to address this limitation.
Refinement (Ref) happens when a potential error is associated with a portion of a value of a composite type. The situation is slightly different between strict potential errors and wrong dynamic types. The following code assigns a pair of two floating-point values to a dynamically typed variable, which is used inconsistently as a pair of an integer and a floating-point.
While the “real” location is the sub-expression
![]() $(2.0\ :: \ \star)$
, SLOG will report the outer pair expression
$(2.0\ :: \ \star)$
, SLOG will report the outer pair expression
![]() $\langle (2.0\ :: \ \star), 1.0 \rangle$
. For strict potential errors, the relevant cast
$\langle (2.0\ :: \ \star), 1.0 \rangle$
. For strict potential errors, the relevant cast
![]() $\langle Int \Leftarrow^b \star \rangle$
is decomposed from a larger cast
$\langle Int \Leftarrow^b \star \rangle$
is decomposed from a larger cast
![]() $\langle Int \times Float \Leftarrow^b \star \rangle$
which will refer to the outer pair expression. For wrong dynamic types, recall that we only use the program label in mapping, while all context refinements are abandoned. Therefore, it can only refer to the outer pair expression.
$\langle Int \times Float \Leftarrow^b \star \rangle$
which will refer to the outer pair expression. For wrong dynamic types, recall that we only use the program label in mapping, while all context refinements are abandoned. Therefore, it can only refer to the outer pair expression.
In our experiment, the location (a syntax tree node) of the false-positive report caused by REF is always the direct parent of the actual bug. Although not in accordance with our Assumption 1, during the classification process we can always find the actual bug directly from the false positive report caused by REF.
Implementation (IMP) is due to a bug Footnote 9 in the Grift compiler itself, the source location information attached to syntax tree nodes is shifted on the first sub-tree of all binding constructs. A false-positive report is classified as IMP if it can be eliminated by fixing this issue.
Among all 1049 false-positive reports of wrong dynamic types, 1020 are due to ESC, 19 are due to REF, and 10 are due to IMP. Among all 655 false-positive reports of strict potential error, 472 are due to ESC, 119 are due to REF, and 64 are due to IMP.
The causes of bugs that cannot be found include non-type (NTY), smashing abstraction(SMASH), and transition (TRAN). The implementation issue mentioned above (IMP) can also make a bug undetectable. Similarly, a scenario is classified as IMP if it can be eliminated by fixing this issue.
Non-type (NTY) means that a scenario does not involve a type-related bug. This category accounts for the vast majority of causes of undetectable bugs. We also estimated the recall of SLOG after removing NTY from all scenarios, noted in Table 3 as column ERecall. We list the two found NTY patterns here.
1. Modifying arithmetic results without affecting the type. An example of this is exchanging the definitions of two variables of the same type.
2. Not altering the program’s semantics. An example of this is exchanging two arguments of the operator “+” while maintaining the same meaning.
Transition (TRAN) is analogous to the escape problem in principle, although it leads to different results. Consider a simple lambda expression that adds 1 to its dynamically typed parameter x and returns the result. If all actual arguments are inconsistent with integer, then the parameter type
![]() $\star$
is a wrong dynamic type, and the use of x in the lambda body will be caught as a strict potential error.
$\star$
is a wrong dynamic type, and the use of x in the lambda body will be caught as a strict potential error.
However, if some actual arguments are inconsistent with integer but others are consistent, then both wrong dynamic errors and strict potential errors will disappear.

This is because, in our definition, an outflow is treated as a strict potential error only if it is inconsistent with all inflows. And wrong dynamic type is defined via strict potential errors. Therefore, a dynamically typed variable cannot be reported as a bug by strict potential errors or wrong dynamic types as long as some of its uses are correct. Thus, TRAN is a trade-off for the increased precision of strict potential error and wrong dynamic type.
Smashing abstraction (SMASH) stems from our smashing abstraction of vectors and tuples. In this model, all elements of a vector or tuple are treated as a single element (Blanchet et al., Reference Blanchet, Cousot, Cousot, Feret, Mauborgne, Miné, Monniaux and Rival2002). For example, consider a vector of type
![]() $\mathrm{\texttt{Vec}}\ \mathrm{\texttt{Int}}$
, one component
$\mathrm{\texttt{Vec}}\ \mathrm{\texttt{Int}}$
, one component
![]() $(1.0\ :: \star)$
has an inconsistent type, but the other components are normally assigned values of type Int. SLOG treats the vector as having only one component, and thus cannot detect potential errors. Therefore, the smashing abstraction stands as one of the inherent shortcomings of Static Blame.
$(1.0\ :: \star)$
has an inconsistent type, but the other components are normally assigned values of type Int. SLOG treats the vector as having only one component, and thus cannot detect potential errors. Therefore, the smashing abstraction stands as one of the inherent shortcomings of Static Blame.
Among all 371 scenarios without strict potential error reports, 352 are due to NTY, 13 are due to TRAN, and 6 are due to SMASH. Among all 372 scenarios without any wrong dynamic type report, 345 are due to NTY, 18 are due to TRAN, 5 are due to SMASH, and 4 are due to IMP.
Overall, we answer RQ1 by concluding that SLOG is able to detect bugs from Grift programs.
5.4.2 RQ2:Performance
For RQ2, Figure 7 shows the results of SLOG on Size, and Figure 8 shows the results of SLOG on Lattice. Recall that Size is a collection where programs increase linearly in size, while Lattice is a collection of 1000 configurations of the same program.

Fig. 7. SLOG performance with respect to program size.

Fig. 8. SLOG performance with respect to the proportion of typed code.
Across the nine measured programs in Size, the run time exhibits quadratic growth with respect to program size. To make it clear, we also record the increment between adjacent points in Figure 7, whose growth is almost linear. In Figure 7, each point in the blue line represents one program in the collection Size, which is created by repeating code in the ray program. The horizontal coordinate of a point is the LOC of this program, while the vertical coordinate is the run time of SLOG. The cyan line records the increment between the adjacent points of the blue line. It has been observed that the performance of SLOG is impacted by the size of the program. The quadratic growth rate is acceptable for relatively small and medium programs. However, its efficiency diminishes when dealing with larger programs.
Figure 8 depicts the variation in SLOG performance in relation to the percentage of typed code. Each point represents one program in the collection Lattice. The horizontal coordinate of a point is the proportion of typed code in this program, while the vertical coordinate is the run time of this program. Figure 8 shows that there is no significant relationship between performance and the proportion of typed code in most cases. However, as the program approaches fully typed, there is a significant increase in the run time of SLOG. In other words, the more precise the type annotations in the program, the slower SLOG runs. This fact may be surprising at first sight because a more precise program should be easier to “check”.
To explain this significant increase more clearly, we also record the number of type flows generated by SLOG in Figure 9. The type flow analysis of Static Blame detects potential errors by continuously traversing the set of type flows and generating new type flows. Therefore, the monotonically increasing set of type flows is the main and necessary cause of the runtime efficiency of SLOG.

Fig. 9. Number of type flows with respect to the proportion of type annotation.
In Figure 9, each data point represents a single program in the Lattice collection. The first sub-figure displays the total number of type flows generated by each program. The horizontal coordinate of a point is the type annotation proportion of the program, while the vertical coordinate is the number of type flows. The first sub-figure of Figure 9 shows the total number of generated type flows increases rapidly as the program approaches fully typed and exhibits the same phenomenon as run time. This indicates that the growth of runtime can be explained by the increase in type flows, as anticipated. To elucidate this phenomenon, we present the second sub-figure, which delves into the underlying reasons for this growth of type flows.
Each point in the second sub-figure is still a program in the Lattice collection. The color represents the proportion of type annotation for each program. The horizontal coordinate of each point is the proportion of dummy type flows among all type flows, while the vertical coordinate of each point still shows the total number of type flows.
The second sub-figure shows the fact that most of the type flows generated are dummy type flows when the program approaches fully static. Therefore, the increase in the number of dummy type flows is the main reason for the rise in run time.
This phenomenon illustrates two points. First, it is very expensive to compute the value passing relations according to Static Blame. Second, the dynamic types in the program “block” further analysis, which greatly reduces the cost of computation of Static Blame.
Overall, we answer RQ2 by concluding that the performance of SLOG is acceptable for programs of small and medium sizes within two or three thousand lines of code. In particular, the run time is quadratic in the size of the program, and the generation of type flows during value passing analysis is the main performance burden.
5.5 Threats to validity
One concern with these experiments is the representativeness of generated bugs. This threat has two aspects: (1) Grift is a simple academic language without many language features and thus a limited set of possible kinds of bugs and (2) the mutation analysis is a coarse approximation of the bugs in real-world programming. Therefore, the experiment may not uncover certain shortcomings of Static Blame.
For instance, our algorithm is unable to handle primitive operators with dynamic types, which is common in gradually typed languages other than Grift (e.g. range in Reticulated Python) and is more challenging to detect statically. However, it is worth noting that these operators are not involved in the benchmark either. Furthermore, the marginal decrease in recall presented in Table 3 also suggests that the bugs injected through mutation may be overly simplistic to detect.
Another concern is the experimental design. Considering that different bugs may influence each other, there is merely one bug per scenario, and therefore do not fully reflect real-world programming, where there may be multiple bugs in a program. Moreover, when the bug code becomes more complex, it becomes more difficult to locate the entire bug from one of its fragments.
The Assumption 1 might not always remain valid. A significant issue arises when the reported bug represents a considerably deep sub-tree of the actual bug. In such cases, the process of locating the actual bug may still require a substantial amount of time. However, in our experiment, almost all bug reports classified as true positives are either the exact bug itself or direct children or grandchildren of the bug, indicating a shallow depth. Consequently, the impact of Assumption 1 on the experiment’s conclusion is minimal, at least within the scope of our experiment.
6 Related work
6.1 Static analysis for gradual typing
Static analysis for gradually typed languages is a relatively unexplored field. Many of the related work focuses on how to optimize the performance of gradually typed language.
6.1.1 Type inference for gradual typing
Although the goal of Static Blame is to statically find potential errors rather than to optimize, the system of Static Blame is highly inspired by Rastogi et al. (Reference Rastogi, Chaudhuri and Hosmer2012), which focuses on optimization by inferring more precise type annotation.
Specifically, Rastogi et al. (Reference Rastogi, Chaudhuri and Hosmer2012) infer gradual types in an ActionScript program by performing a flow-based constraint analysis for each type variable, eventually computing an upper bound for them. Type flows are exactly the expression form of these constraints. However, the main difference is that they do not reject any programs as their goal is optimization. They also do not discuss how to use type flow to characterize possible errors in programs.
Type migration is the process of making a gradually typed program more precise by replacing dynamic annotations (
![]() $\star$
) with more static inferred types. While Rastogi et al. (Reference Rastogi, Chaudhuri and Hosmer2012) focus on performing type migration, Campora et al. (Reference Campora, Chen, Erwig and Walkingshaw2017) are recognized for explicitly proposing the type migration problem. The problem of migrating gradual types is closely related to this article. A key similarity between our work and research on type migration lies in the need to analyze the data flow within a program in the presence of dynamic types.
$\star$
) with more static inferred types. While Rastogi et al. (Reference Rastogi, Chaudhuri and Hosmer2012) focus on performing type migration, Campora et al. (Reference Campora, Chen, Erwig and Walkingshaw2017) are recognized for explicitly proposing the type migration problem. The problem of migrating gradual types is closely related to this article. A key similarity between our work and research on type migration lies in the need to analyze the data flow within a program in the presence of dynamic types.
However, in the case of type migration, it is common to employ a type inference algorithm rather than conducting direct flow analysis, which distinguishes it from our approach. And as Rastogi et al. (Reference Rastogi, Chaudhuri and Hosmer2012), another main difference is that type migration does not reject programs statically and does not analyze potential errors in the program. Campora et al. (Reference Campora, Chen, Erwig and Walkingshaw2017) try to solve the problem of large search spaces in gradual type migration by variational typing. They use a unification-based algorithm and try to find the most static migration for programs. Phipps-Costin et al. (Reference Phipps-Costin, Anderson, Greenberg and Guha2021) use an external third-party off-shelf constraint solver to perform type migration and can generate different alternative solutions to suit different requirements by means of soft variables. Migeed and Palsberg (Reference Migeed and Palsberg2020) study several properties of type migration in terms of the theory of computation. In particular, whether the maximal migration problem is decidable or not is still an open problem.
Much of the academic research on gradual typing inference is based on one principle: only inferring static types for type variables. This principle is implicitly captured in the breakthrough paper Siek and Vachharajani (Reference Siek and Vachharajani2008), where they propose a unification-based algorithm but without generating dynamic types to resolve static inconsistencies. Garcia and Cimini (Reference Garcia and Cimini2015) then formally introduce this principle and proved the equivalence of their algorithm to Siek and Vachharajani (Reference Siek and Vachharajani2008). This principle simplifies the complexity of migrating the type inference algorithms of existing static type systems to gradual counterparts.
Soft typing (Wright & Cartwright, Reference Wright and Cartwright1997) also discusses code that will fail caused by erroneous data flows, much like our strict potential error. The main difference is that Static Blame targets gradually typed language, while Wright and Cartwright (Reference Wright and Cartwright1997) target Scheme. Gradually typed languages perform more checks and guarantee that an error will occur when dynamic inconsistency is detected. Scheme, as a dynamically typed language, does not have this guarantee. Thus, Static Blame focuses on how to characterize the behavior when an error occurs, while Wright and Cartwright (Reference Wright and Cartwright1997) must control the behavior of the program by explicitly injecting error.
6.1.2 Detection of inconsistency
Another work related to inconsistency is how to detect incorrect annotations and fix them. Campora and Chen (Reference Campora and Chen2020) have proposed a method to fix “wrong type annotations” in a gradually typed program by exploratory typing, where they use a type inference algorithm to get alternatives for type annotations in a program. By exploring different choices of these alternatives, they find wrong type annotations and try to compute fixes for them.
Fixing wrong annotations is similar to our work in the detection of impedance mismatches between type annotations and program behavior. The difference is that we start from the assumption that the annotations are correct, while the concrete implementation may be wrong. Again, our main work is to establish the relationship between the checked potential errors and the actual errors at runtime.
However, the literature has many challenges to the assumption that annotations are correct. The problem of wrong annotations is observed in real-world optionally typed languages (Feldthaus & Møller, Reference Feldthaus and Møller2014) and is ubiquitous when migrating from dynamic to static, where numerous interfaces are needed to be annotated manually. Williams et al. (Reference Williams, Morris, Wadler and Zalewski2017) detected a significant number of mismatches between annotations and implementations in TypeScript projects. This problem is difficult to tackle by gradual typing theory because of the dynamic nature of JavaScript.
6.2 Blame mechanism
The blame mechanism in gradually typed languages comes from the study of high-order contracts (Findler & Felleisen, Reference Findler and Felleisen2002), where type annotations can be considered a kind of contract. Academically, the blame mechanism is a tool for characterizing program behavior in the absence of type safety. Wadler and Findler (Reference Wadler and Findler2009) use a number of subtyping relations to formalize and prove a slogan that well-typed components cannot be blamed, i.e., if a cast fails at runtime it must blame the more imprecise side of the cast. It can be viewed as a complete method for finding error casts statically. Our search for normal potential errors is also a complete method, but slightly more precise because we analyze the program globally rather than just comparing type precision for every cast. Blame mechanism is also an important characterization tool of the well-known criteria for gradual typing proposed by Siek et al. (Reference Siek, Vitousek, Cimini, Tobin-Hochstadt and Garcia2015), which also became the subsequent design guidelines for gradually typed languages (Garcia et al., Reference Garcia, Clark and Tanter2016; Igarashi et al., Reference Igarashi, Sekiyama and Igarashi2017).
Practically, the blame mechanism is designed to help programmers debug runtime type errors. However, there are few industrial languages implementing blame mechanism. The most popular languages that combine dynamic and static typing do not perform any checks at runtime, like TypeScript et al. This is partly because of the large runtime overhead associated with dynamic checks and partly because the effectiveness of blame is questionable. Lazarek et al. (Reference Lazarek, Greenman, Felleisen and Dimoulas2021) evaluate the usefulness of the blame mechanism for debugging by mutation analysis and conclude that blame information can only help in a slight margin. Greenman et al. (Reference Greenman, Felleisen and Dimoulas2019) theoretically prove the effectiveness of a more accurate blame mechanism by adapting complete monitoring to gradual typing.
6.3 Different semantics and extension of gradual typing
Our work relies heavily on cast semantics, while gradual typing has many different semantics. The transient semantics (Vitousek et al., Reference Vitousek, Kent, Siek and Baker2014) is proposed to get better performance at the cost of sacrificing precision since the general cast semantics has performance problems (Takikawa et al., Reference Takikawa, Feltey, Greenman, New, Vitek and Felleisen2016). Concrete Semantics (Wrigstad et al., Reference Wrigstad, Nardelli, Lebresne, Östlund and Vitek2010; Muehlboeck & Tate, Reference Muehlboeck and Tate2017; Richards et al., Reference Richards, Nardelli and Vitek2015; Lu et al., Reference Lu, Greenman, Meyer, Viehland, Panse and Krishnamurthi2022), on the other hand, maintains additional type information for each value, optimizing the performance of gradual typing at the cost of expressiveness. In addition, gradual typing has many different strategies for handling memory, such as the guarded reference (Herman et al., Reference Herman, Tomb and Flanagan2010) which is the semantics supported by our implementation on Grift; the monotonic reference (Siek et al., Reference Siek, Vitousek, Cimini, Tobin-Hochstadt and Garcia2015) and the AGT-induced semantics (Toro & Tanter, Reference Toro and Tanter2020). Therefore, exploring how to establish a correlation between type flow and these semantics is important for future work.
The concept of context labels shares some similarities with the concept of tags in Vitousek et al. (Reference Vitousek, Swords and Siek2017), which also defines a concept “labeled type”. However, the usage and definition of these concepts differ significantly. In Vitousek et al. (Reference Vitousek, Swords and Siek2017), a labeled type is simply a compiled type cast. Let
![]() $\langle T \Leftarrow^b S \rangle$
be a type cast, the labeled type
$\langle T \Leftarrow^b S \rangle$
be a type cast, the labeled type
![]() $[\![ \langle T \Leftarrow^b S \rangle ]\!]$
it compiles to encodes two kinds of information:
$[\![ \langle T \Leftarrow^b S \rangle ]\!]$
it compiles to encodes two kinds of information:
1. The blame label b is associated with the type cast.
2. For each element in the type structure, whether or not the type cast is responsible for introducing that specific portion of type.
For example,
![]() $[\![ \langle \star \to \mathrm{\texttt{int}} \Leftarrow^b \mathrm{\texttt{int}} \to \mathrm{\texttt{int}} \rangle ]\!] = \mathrm{\texttt{int}}^b \to^\epsilon \mathrm{\texttt{int}}^\epsilon$
. This cast is responsible for introducing the argument type
$[\![ \langle \star \to \mathrm{\texttt{int}} \Leftarrow^b \mathrm{\texttt{int}} \to \mathrm{\texttt{int}} \rangle ]\!] = \mathrm{\texttt{int}}^b \to^\epsilon \mathrm{\texttt{int}}^\epsilon$
. This cast is responsible for introducing the argument type
![]() $\star$
, and any check failure caused by non-int arguments should blame this cast. Therefore, there is a blame label b in the argument position of the labeled type. Tags (ARG, RES,…) are used to locate specific portion in labeled types. In conclusion, labeled types and tags serve to store and query blame information in Vitousek et al. (Reference Vitousek, Swords and Siek2017).
$\star$
, and any check failure caused by non-int arguments should blame this cast. Therefore, there is a blame label b in the argument position of the labeled type. Tags (ARG, RES,…) are used to locate specific portion in labeled types. In conclusion, labeled types and tags serve to store and query blame information in Vitousek et al. (Reference Vitousek, Swords and Siek2017).
However, while Vitousek et al. (Reference Vitousek, Swords and Siek2017) focuses on designing gradual typing semantics, this paper concentrates on static analysis. Context labels in our work are utilized to identify and track the evaluation of expressions in the source codes. Technically, context labels in our work do not affect program execution and are mainly used to generate unique names in analysis.
The potential error that Static Blame focuses on is caused by imprecision in gradual types. Some related work attempts to increase the precision of gradual types while preserving flexibility. Toro and Tanter (Reference Toro and Tanter2017) devise gradual union types, combining tagged and untagged concatenation types using the AGT approach. Castagna et al. (Reference Castagna, Lanvin, Petrucciani and Siek2019) combine set-theoretic types with gradual types. They map gradual types to sets of types, thus providing a semantic interpretation of gradual types. These extensions improve the expressiveness of the type system, and programmers can thus allow the type system to statically rule out potential errors by avoiding the use of dynamic types. However, this type of work is orthogonal to Static Blame. Dynamic types are still allowed to exist in these systems, and explicitly annotated dynamic types will still hide problematic data flows.
7 Conclusion and future work
The Static Blame framework reveals data flows mediated by dynamic types and establishes the correspondence between data flows found and runtime behavior for gradual typing programs. To do so, the data flows are modeled by the notion of type flow, while the runtime behavior is characterized by type casts, and we demonstrate a straightforward correspondence between them.
The main effect of the Static Blame framework is to provide an additional static check for gradual typing programs and compensate for the weak static checking ability of the gradual type system. It formally demonstrates how the checked problem affects the execution of programs. Our evaluation shows that Static Blame can catch potential errors that are ignored by the gradual type system, while its performance is acceptable.
Future work will focus on extending the framework to more complex type systems and different runtime semantics. In addition, we also plan to combine Static Blame with traditional flow analysis techniques. In particular, we plan to optimize the performance of type flow analysis, reduce the overhead of dummy type flows, and add flow-sensitive analysis to Static Blame.
Acknowledgments
The authors thank the anonymous JFP reviewers for their constructive comments and suggestions. This work was supported by the National Natural Science Foundation of China (grant numbers 62272221, 62172202, 62172205) and the Cooperation Fund of Nanjing University-Huawei Novel Software Technology Lab (grant number TC20230202021-2023-10). The second author Lin Chen is the corresponding author.
Conflicts of interest
The authors report no conflict of interest.






















Discussions
No Discussions have been published for this article.