We have numerically investigated the interaction dynamics between two rigid spherical particles moving in a fluid-filled cylinder that is rotating at a constant speed. The cylinder rotation is about a horizontal axis. The particle densities are less than that of the fluid. The numerical procedure employed to solve the mathematical formulation is based on a three-dimensional arbitrary Larangian–Eulerian (ALE), moving mesh finite-element technique, described in a frame of reference rotating with the cylinder. Results are obtained in the ranges of particle Reynolds number, 1 <Rep≤60, and shear Reynolds number, 1≤Res<10. Two identical particles, depending on initial conditions at release, approach each other (‘drafting’ and ‘kissing’), tumble in the axial direction, and axially migrate towards opposing transverse planes on which they ‘settle’ (settling planes). Under some other initial conditions, the particles migrate directly onto their settling planes. For two identical particles, the settling planes are equidistant from the mid-transverse plane of the cylinder and the locations of the planes are determined by particle–particle and particle–wall force balances. Furthermore, for identical particles and given values of Rep and Res, the locations of such settling planes remain the same, independent of the initial conditions at release. While located on these settling planes, as viewed in an inertial frame, the particles may attain three possible distinct states depending on the values of the Reynolds numbers. In one state (low Rep, high Res), the particles attain and remain at fixed equilibrium points on their settling planes. In the second (all Rep, low Res), they execute spiralling motions about fixed points on their respective settling planes. These fixed points coincide with the locations of the equilibrium point which would occur on the mid-axial plane in the case of a single particle. In the third state (low Rep, moderate Res or high Rep, moderate to high Res), they execute near-circular orbital motion on their respective settling planes, again about fixed points. These fixed points also coincide with the locations of the equilibrium points corresponding to single-particle dynamics. Both the spiral and near-circular motions of the particles occur in an out-of-phase manner with regard to their radial positions about the fixed point; the near-circular out-of-phase motion resembles bicycle pedalling. Also, in the second and third states, the particles simultaneously experience very weak axial oscillations about their settling planes, the frequency of such oscillations coinciding with the frequency of rotation of the circular cylinder.
The behaviours of two non-identical particles (same density but different sizes, or same size but different densities) are different from those of identical particles. For example, non-identical particles may both end up settling on the mid-axial plane. This occurs when the locations of their corresponding single-particle equilibrium points are far apart. When such points are not far apart, particles may settle on planes that may not be symmetrical about the mid-axial plane. While located on their settling planes, their equilibrium states may not be similar. For example, for particles of the same density but of different sizes, the smaller of the two may execute a spiralling motion while the larger is in near-circular orbital motion. With particles of the same size but of different densities, while the lighter of the two approaches its equilibrium point on the mid-axial plane, the heavier one experiences a circular motion on the same plane about its equilibrium point. A major reason for the eventual attainment of these various states is noted to be the interplay between the particle–particle and particle–wall forces.




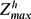 /
/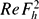 is above a threshold estimated as 340. Movies are available with the online version of the paper.
is above a threshold estimated as 340. Movies are available with the online version of the paper.