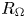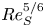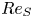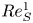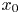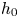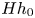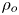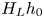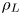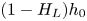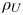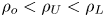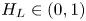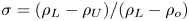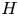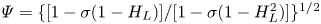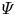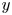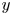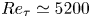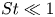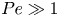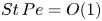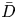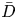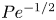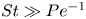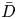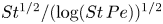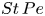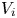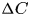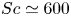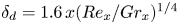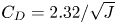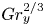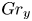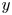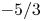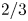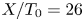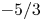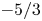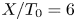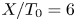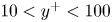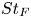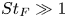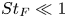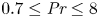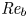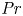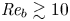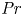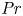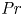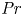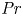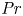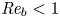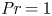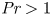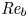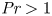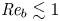JFM Rapids
On the dispersion of entropy waves in turbulent flows
-
- Published online by Cambridge University Press:
- 17 September 2020, R1
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Generation and decay of counter-rotating vortices downstream of yawed wind turbines in the atmospheric boundary layer
-
- Published online by Cambridge University Press:
- 22 September 2020, R2
-
- Article
-
- You have access
- HTML
- Export citation
Extreme water-wave profile recovery from pressure measurements at the seabed
-
- Published online by Cambridge University Press:
- 28 September 2020, R3
-
- Article
- Export citation
Exact relations between Rayleigh–Bénard and rotating plane Couette flow in two dimensions
-
- Published online by Cambridge University Press:
- 28 September 2020, R4
-
- Article
- Export citation
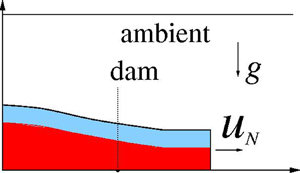
A model for the propagation of inertial gravity currents released from a two-layer stratified lock
-
- Published online by Cambridge University Press:
- 01 October 2020, R5
-
- Article
- Export citation
The mean logarithm emerges with self-similar energy balance
-
- Published online by Cambridge University Press:
- 01 October 2020, R6
-
- Article
- Export citation
Focus on Fluids
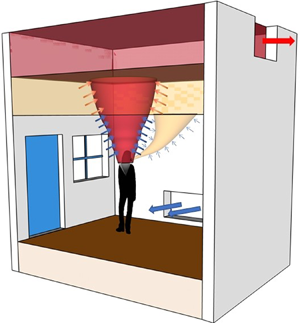
Effects of ventilation on the indoor spread of COVID-19
-
- Published online by Cambridge University Press:
- 28 September 2020, F1
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
JFM Papers
The dynamics of stratified horizontal shear flows at low Péclet number
-
- Published online by Cambridge University Press:
- 17 September 2020, A1
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
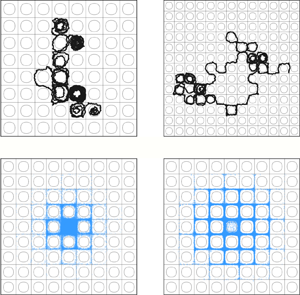
Dispersion of inertial particles in cellular flows in the small-Stokes, large-Péclet regime
-
- Published online by Cambridge University Press:
- 17 September 2020, A2
-
- Article
- Export citation
Scaling in concentration-driven convection boundary layers with transpiration
-
- Published online by Cambridge University Press:
- 17 September 2020, A3
-
- Article
- Export citation
Energy transfer in turbulent flows behind two side-by-side square cylinders
-
- Published online by Cambridge University Press:
- 18 September 2020, A4
-
- Article
- Export citation
A hyperbolic two-fluid model for compressible flows with arbitrary material-density ratios
-
- Published online by Cambridge University Press:
- 18 September 2020, A5
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Experimental study on low-speed streaks in a turbulent boundary layer at low Reynolds number
-
- Published online by Cambridge University Press:
- 18 September 2020, A6
-
- Article
- Export citation
Stochastic models for capturing dispersion in particle-laden flows
-
- Published online by Cambridge University Press:
- 18 September 2020, A7
-
- Article
- Export citation
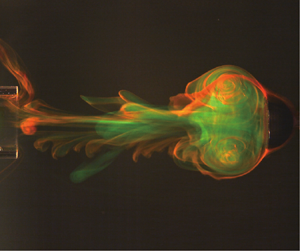
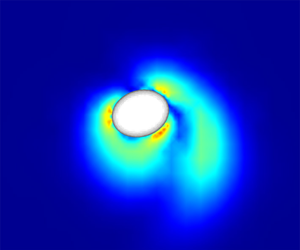
Vortex ring formation coupled with a translating bluff body
-
- Published online by Cambridge University Press:
- 18 September 2020, A8
-
- Article
- Export citation
Deflected wake interaction of tandem flapping foils
-
- Published online by Cambridge University Press:
- 18 September 2020, A9
-
- Article
- Export citation
Chaotic orbits of tumbling ellipsoids
-
- Published online by Cambridge University Press:
- 21 September 2020, A10
-
- Article
- Export citation
Stability of dancing Volvox
-
- Published online by Cambridge University Press:
- 21 September 2020, A11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Prandtl number dependence of stratified turbulence
-
- Published online by Cambridge University Press:
- 21 September 2020, A12
-
- Article
- Export citation
Gabor mode enrichment in large eddy simulations of turbulent flow
-
- Published online by Cambridge University Press:
- 21 September 2020, A13
-
- Article
- Export citation