Hostname: page-component-848d4c4894-mwx4w Total loading time: 0 Render date: 2024-06-19T09:29:45.760Z Has data issue: false hasContentIssue false
  • English
  • Français

Wake behind a three-dimensional dry transom stern. Part 2. Analysis and modelling of incompressible highly variable density turbulence

Published online by Cambridge University Press:  26 July 2019

Kelli Hendrickson Open the ORCID record for Kelli Hendrickson [Opens in a new window]  and
Dick K.-P. Yue Open the ORCID record for Dick K.-P. Yue [Opens in a new window]
Kelli Hendrickson*
Affiliation:
Department of Mechanical Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
Dick K.-P. Yue
Affiliation:
Department of Mechanical Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
*
†Email address for correspondence: khendrk@mit.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

We analyse the turbulence characteristics and consider the closure modelling of the air entraining flow in the wake of three-dimensional, rectangular dry transom sterns obtained using high-resolution implicit large eddy simulations (iLES) (Hendrickson et al., J. Fluid Mech., vol. 875, 2019, pp. 854–883). Our focus is the incompressible highly variable density turbulence (IHVDT) in the near surface mixed-phase region 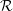${\mathcal{R}}$ behind the stern. We characterize the turbulence statistics in 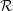${\mathcal{R}}$ and determine it to be highly anisotropic due to quasi-steady wave breaking. Using unconditioned Reynolds decomposition for our analysis, we show that the turbulent mass flux (TMF) is important in IHVDT for the production of turbulent kinetic energy and is as relevant to the mean momentum equations as the Reynolds stresses. We develop a simple, regional explicit algebraic closure model for the TMF based on a functional relationship between the fluxes and tensor flow quantities. A priori tests of the model show mean density gradients and buoyancy effects are the main driving parameters for predicting the turbulent mass flux and the model is capable of capturing the highly localized nature of the TMF in 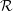${\mathcal{R}}$.

JFM classification

Waves/Free-surface Flows: Wave breaking Multiphase and Particle-laden Flows: Multiphase flow
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 875 , 25 September 2019 , pp. 884 - 913
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aliod, R. & Dopazo, C. 1990 A statistically conditioned averaging formalism for deriving two-phase flow equations. Part. Part. Syst. Charact. 7 (1-4), 191–202.Google Scholar
Aspden, A., Nikiforkakis, N., Dalziel, S. & Bell, J. B. 2008 Analysis of implicit LES methods. Commun. Appl. Maths Comput. Sci. 3 (1), 103–126.Google Scholar
Balachandar, S. & Eaton, J. K. 2010 Turbulent dispersed multiphase flow. Annu. Rev. Fluid Mech. 42 (1), 111–133.Google Scholar
Baldy, S. 1993 A generation-dispersion model of ambient and transient bubbles in the close vicinity of breaking waves. J. Geophys. Res. 98 (C10), 18277–18293.Google Scholar
Banerjee, S., Krahl, R., Durst, F. & Zenger, C. 2007 Presentation of anisotropy properties of turbulence, invariants versus eigenvalue approaches. J. Turbul. 8, N32.Google Scholar
Brocchini, M. & Peregrine, D. H. 2001 The dynamics of strong turbulence at free surfaces. Part 2. Free-surface boundary conditions. J. Fluid Mech. 449, 255–290.Google Scholar
Bunner, B. & Tryggvason, G. 2002a Dynamics of homogeneous bubbly flows. Part 1. Rise velocity and microstructure of the bubbles. J. Fluid Mech. 466, 17–52.Google Scholar
Bunner, B. & Tryggvason, G. 2002b Dynamics of homogeneous bubbly flows. Part 2. Velocity fluctuations. J. Fluid Mech. 466, 53–84.Google Scholar
Chachereau, Y. & Chanson, H. 2011 Bubbly flow measurements in hydraulic jumps with small inflow Froude numbers. Intl J. Multiphase Flow 37 (6), 555–564.Google Scholar
Chassaing, P., Antonia, R. A., Anselmet, F., Joly, L. & Sarkar, S. 2002 Variable Density Fluid Turbulence. Kluwer Academic.Google Scholar
Dakos, T. & Gibson, M. M. 1987 On modelling the pressure terms of the scalar flux equations. In Turbulent Shear Flows 5, pp. 7–18. Springer.Google Scholar
Daly, B. J. & Harlow, F. H. 1970 Transport equations in turbulence. Phys. Fluids 13 (11), 2634–2649.Google Scholar
Deane, G. B. & Stokes, M. D. 2002 Scale dependence of bubble creation mechanisms in breaking waves. Nature 418 (6900), 839–844.Google Scholar
Dimotakis, P. E. 2005 Turbulent mixing. Annu. Rev. Fluid Mech. 37 (1), 329–356.Google Scholar
Dodd, M. S. & Ferrante, A. 2016 On the interaction of Taylor length scale size droplets and isotropic turbulence. J. Fluid Mech. 806, 356–412.Google Scholar
Drazen, D. A., Fullerton, A. M., Fu, T. C., Beale, K. L. C., O’Shea, T. T., Brucker, K. A., Dommermuth, D. G., Wyatt, D. C., Bhushan, S., Carrica, P. M. et al. 2010 A comparison of model-scale experimental measurements and computational predictions for a large transom-stern wave. In Proceedings 28th Symp. on Naval Ship Hydrodynamics. Pasadena, California. US Office of Naval Research.Google Scholar
Drew, D. A. 1983 Mathematical modeling of two-phase flow. Annu. Rev. Fluid Mech. 15 (1), 261–291.Google Scholar
Duranti, S. & Pittaluga, F. 2000 Navier–Stokes prediction of internal flows with a three-equation turbulence model. AIAA J. 38 (6), 1098–1100.Google Scholar
Emory, M. & Iaccarino, G.2014 Visualizing turbulence anisotropy in the spatial domain with componentality contours. Annual Research Briefs. Center for Turbulence Research.Google Scholar
Favre, A. 1969 Statistical equations of turbulent gases. Probl. Hydrodyn. Contin. Mech. 231–266.Google Scholar
Friedberg, R. & Cameron, J. E. 1970 Test of the Monte Carlo method: fast simulation of a small ising lattice. J. Chem. Phys. 52 (12), 6049–6058.Google Scholar
Fu, T. C., Fullerton, A. M., Terrill, E. J. & Lada, G. 2006 Measurements of the wave fields around the R/V Athena I. In Proceedings 26th Symp. on Naval Ship Hydrodynamics. Strategic Analysis, Inc.Google Scholar
Gui, L., Longo, J. & Stern, F. 2001 Towing tank PIV measurement system, data and uncertainty assessment for DTMB Model 5512. Exp. Fluids 31 (3), 336–346.Google Scholar
He, X., Zhang, R., Chen, S. & Doolen, G. D. 1999 On the three-dimensional Rayleigh–Taylor instability. Phys. Fluids 11 (5), 1143–1152.Google Scholar
Hendrickson, K., Weymouth, G., Yu, X. & Yue, D. K.-P. 2019 Wake behind a three-dimensional dry transom stern. Part 1. Flow structure and large-scale air entrainment. J. Fluid Mech. 875, 854–883.Google Scholar
Jovanovic, J. 2004 The Statistical Dynamics of Turbulence. Springer.Google Scholar
Kang, C., Zhang, W., Gu, Y. & Mao, N. 2017 Bubble size and flow characteristics of bubbly flow downstream of a ventilated cylinder. Chem. Engng Res. Des. 122, 263–272.Google Scholar
Karn, A., Shao, A., Arndt, R. E. A. & Hong, J. 2016 Bubble coalescence and breakup in turbulent bubbly wake of a ventilated hydrofoil. Exp. Therm. Fluid Sci. 70, 397–407.Google Scholar
Kim, W. J., Van, S. H. & Kim, D. H. 2001 Measurement of flows around modern commercial ship models. Exp. Fluids 31 (5), 567–578.Google Scholar
Lance, M. & Bataille, J. 1991 Turbulence in the liquid phase of a uniform bubbly air–water flow. J. Fluid Mech. 222, 95–118.Google Scholar
Larsson, L., Stern, F. & Betram, V. 2003 Benchmarking of computational fluid dynamics for ship flows: the Gothenburg 2000 Workshop. J. Ship Res. 47 (1), 63–81.Google Scholar
Larsson, L., Stern, F. & Visonneau, M.(Eds) 2013 Numerical Ship Hydrodynamics: An Assessment of the Gothenburg 2010 Workshop. Springer.Google Scholar
Launder, B. E. 1975 Heat and mass transport. In Turbulence (ed. Bradshaw, P.), pp. 231–287. Springer.Google Scholar
List, E. J. 1982 Turbulent jets and plumes. Annu. Rev. Fluid Mech. 14 (1), 189–212.Google Scholar
Livescu, D. & Ristorcelli, J. R. 2007 Buoyancy-driven variable-density turbulence. J. Fluid Mech. 591, 43–71.Google Scholar
Livescu, D. & Ristorcelli, J. R. 2008 Variable-density mixing in buoyancy-driven turbulence. J. Fluid Mech. 605, 145–180.Google Scholar
Lumley, J. L. & Newman, G. R. 1977 The return to isotropy of homogeneous turbulence. J. Fluid Mech. 82 (1), 161–178.Google Scholar
Ma, G., Shi, F. & Kirby, J. T. 2011a A polydisperse two-fluid model for surf zone bubble simulation. J. Geophys. Res. 116, C05010.Google Scholar
Ma, J., Oberai, A. A., Hyman, M. C., Drew, D. A. Jr & Lahey, R. T. L. 2011b Two-fluid modeling of bubbly flows around surface ships using a phenomenological subgrid air entrainment model. Comput. Fluids 52, 50–57.Google Scholar
Martínez-Legazpi, P., Rodríguez-Rodríguez, J., Marugán-Cruz, C. & Lasheras, J. C. 2013 Plunging to spilling transition in corner surface waves in the wake of a partially submerged vertical plate. Exp. Fluids 54 (1), 1–11.Google Scholar
Morales, J. J., Nuevo, M. J. & Rull, L. F. 1990 Statistical error methods in computer simulations. J. Comput. Phys. 89 (2), 432–438.Google Scholar
Mortazavi, M., Le Chenadec, V., Moin, P. & Mani, A. 2016 Direct numerical simulation of a turbulent hydraulic jump: turbulence statistics and air entrainment. J. Fluid Mech. 797, 60–94.Google Scholar
Mudde, R. F. 2005 Gravity-driven bubbly flows. Annu. Rev. Fluid Mech. 37 (1), 393–423.Google Scholar
Olivieri, A., Pistani, F., Avanzini, A., Stern, F. & Penna, R.2001 Towing tank experiments of resistance, sinkage and trim, boundary layer, wake, and free surface flow around a naval combatant INSEAN 2340 model. Tech. Rep. Iowa Univ Iowa City Coll of Engineering.Google Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.Google Scholar
Ratcliffe, T. 1998 Validation of free surface Reynolds averaged Navier–Stokes and potential flow codes. In Proceedings 22nd Symp. on Naval Ship Hydrodynamics, pp. 964–980. National Academy Press.Google Scholar
Rouse, H., Bhoota, B. V. & Hsu, E.-Y. 1949 Design of channel expansions. Proc. ASCE 75 (9), 1369–1385.Google Scholar
Sarkar, S. & Lakshmanan, B. 1991 Application of a Reynolds stress turbulence model to the compressible shear layer. AIAA J. 29 (5), 743–749.Google Scholar
Sharp, D. H. 1984 An overview of Rayleigh–Taylor instability. Physica D 12 (1), 3–18.Google Scholar
Shen, L., Zhang, C. & Yue, D. K.-P. 2002 Free-surface turbulent wake behind towed ship models: experimental measurements, stability analyses and direct numerical simulations. J. Fluid Mech. 469, 89–120.Google Scholar
Shih, T.-H., Lumley, J. L. & Janicka, J. 1987 Second-order modelling of a variable-density mixing layer. J. Fluid Mech. 180, 93–116.Google Scholar
Sotiropoulos, F. & Patel, V. C. 1995 Application of Reynolds-stress transport models to stern and wake flows. J. Ship Res. 39 (4), 263–283.Google Scholar
Taulbee, D. & VanOsdol, J.1991 Modeling turbulent compressible flows – the mass fluctuating velocity and squared density. AIAA Paper 91-524, pp. 1–9.Google Scholar
Terrill, E. J. & Fu, T. C. 2008 At-sea measurements for ship hydromechanics. In Proceedings of 27th Symp. on Naval Ship Hydrodynamics, vol. 1. US Office of Naval Research.Google Scholar
Wei, X., Zhang, J. & Zhou, L. 2004 A new algebraic mass flux model for simulating turbulent mixing in swirling flow. Numer. Heat Tr. B-Fund. 45 (3), 283–300.Google Scholar
Weymouth, G. D. & Yue, D. K.-P. 2010 Conservative volume-of-fluid method for free-surface simulations on cartesian-grids. J. Comput. Phys. 229 (8), 2853–2865.Google Scholar
Weymouth, G. D. & Yue, D. K.-P. 2011 Boundary data immersion method for Cartesian-grid simulations of fluid-body interaction problems. J. Comput. Phys. 230 (16), 6233–6247.Google Scholar
Yoshizawa, A., Liou, W. W., Yokoi, N. & Shih, T.-H. 1997 Modeling compressible effects on the Reynolds stress using Markovianized two-scale method. Phys. Fluids 9 (10), 3024–3036.Google Scholar
Young, Y. L., Harwood, C. M., Miguel Montero, F., Ward, J. C. & Ceccio, S. L. 2017 Ventilation of lifting bodies: review of the physics and discussion of scaling effects. Appl. Mech. Rev. 69 (1), 010801–010801–38.Google Scholar
Younis, B. A., Speziale, C. G. & Clark, T. T. 2005 A rational model for the turbulent scalar fluxes. Proc. R. Soc. Lond. A 461 (2054), 575–594.Google Scholar