Hostname: page-component-8448b6f56d-mp689 Total loading time: 0 Render date: 2024-04-25T06:52:26.348Z Has data issue: false hasContentIssue false
  • English
  • Français

Vortex-induced vibration prediction via an impedance criterion

Published online by Cambridge University Press:  04 March 2020

D. Sabino Open the ORCID record for D. Sabino [Opens in a new window] ,
D. Fabre Open the ORCID record for D. Fabre [Opens in a new window] ,
J. S. Leontini Open the ORCID record for J. S. Leontini [Opens in a new window]  and
D. Lo Jacono Open the ORCID record for D. Lo Jacono [Opens in a new window]
D. Sabino*
Affiliation:
Institut de Mécanique des Fluides de Toulouse (IMFT), Université de Toulouse, CNRS, Toulouse, France
D. Fabre
Affiliation:
Institut de Mécanique des Fluides de Toulouse (IMFT), Université de Toulouse, CNRS, Toulouse, France
J. S. Leontini
Affiliation:
Swinburne University of Technology, Hawthorn, Victoria, 3122, Australia
D. Lo Jacono
Affiliation:
Institut de Mécanique des Fluides de Toulouse (IMFT), Université de Toulouse, CNRS, Toulouse, France
*
†Email address for correspondence: diogo.ferreirasabino@imft.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

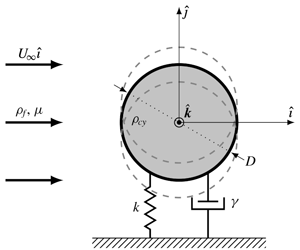
The vortex-induced vibration of a spring-mounted, damped, rigid circular cylinder, immersed in a Newtonian viscous flow and capable of moving in the direction orthogonal to the unperturbed flow is investigated for Reynolds numbers $Re$ in the vicinity of the onset of unsteadiness ($15\leqslant Re\leqslant 60$) using the incompressible linearised Navier–Stokes equations. In a first step, we solve the linear problem considering an imposed harmonic motion of the cylinder. Results are interpreted in terms of the mechanical impedance, i.e. the ratio between the vertical force coefficient and the cylinder velocity, which is represented as function of the Reynolds number and the driving frequency. Considering the energy transfer between the cylinder and the fluid, we show that impedance results provide a simple criterion allowing the prediction of the onset of instability of the coupled fluid-elastic structure case. A global stability analysis of the fully coupled fluid/cylinder system is then performed. The instability thresholds obtained by this second approach are found to be in perfect agreement with the predictions of the impedance-based criterion. A theoretical argument, based on asymptotic developments, is then provided to give a prediction of eigenvalues of the coupled problem, as well as to characterise the region of instability beyond the threshold as function of the reduced velocity $U^{\ast }$, the dimensionless mass $m^{\ast }$ and the Reynolds number. The influence of the damping parameter $\unicode[STIX]{x1D6FE}$ on the instability region is also explored.

JFM classification

Vortex Flows: Vortex shedding Instability: Parametric instability
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 890 , 10 May 2020 , A4
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bearman, P. W. 2011 Circular cylinder wakes and vortex-induced vibrations. J. Fluids Struct. 27 (5), 648–658.CrossRefGoogle Scholar
Bishop, R. & Hassan, A. 1964 The lift and drag forces on a circular cylinder oscillating in a flowing fluid. Proc. R. Soc. Lond. 277, 51–75.Google Scholar
Brezzi, F. & Fortin, M. 1991 Mixed and Hybrid Finite Element Methods. Springer.CrossRefGoogle Scholar
Buffoni, E. 2003 Vortex shedding in subcritical conditions. Phys. Fluids 15 (3), 814–816.CrossRefGoogle Scholar
Conciauro, G. & Puglisi, M.1981 Meaning of the negative impedance. NASA STI/Recon Tech. Rep. N 82.CrossRefGoogle Scholar
Cossu, C. & Morino, L. 2000 On the instability of a spring-mounted circular cylinder in a viscous flow at low Reynolds numbers. J. Fluids Struct. 14 (2), 183–196.CrossRefGoogle Scholar
Dušek, J., Le Gal, P. & Frainié, P. 1994 A numerical and theoretical study of the first Hopf bifurcation in a cylinder wake. J. Fluid Mech. 264, 59–80.CrossRefGoogle Scholar
Fabre, D., Assemat, P. & Magnaudet, J. 2011 A quasi-static approach to the stability of the path of heavy bodies falling within a viscous fluid. J. Fluids Struct. 27 (5), 758–767.CrossRefGoogle Scholar
Fabre, D., Citro, V., Ferreira Sabino, D., Bonnefis, P., Sierra, J., Giannetti, F. & Pigou, M. 2018 A practical review on linear and nonlinear global approaches to flow instabilities. Appl. Mech. Rev. 70, 060802.CrossRefGoogle Scholar
Fabre, D., Longobardi, R., Citro, V. & Luchini, P. 2020 Acoustic impedance and hydrodynamic instability of the flow through a circular aperture in a thick plate. J. Fluid Mech. 885, A11.CrossRefGoogle Scholar
Feng, C. C.1968 The measurement of vortex induced effects in flow past stationary and oscillating circular and d-section cylinders. PhD thesis, The University of British Columbia, Canada.Google Scholar
Giannetti, F. & Luchini, P. 2007 Structural sensitivity of the first instability of the cylinder wake. J. Fluid Mech. 581, 167–197.CrossRefGoogle Scholar
Griffin, O. M., Skop, R. A. & Koopmann, G. H. 1973 The vortex-excited resonant vibrations of circular cylinders. J. Sound Vib. 31 (2), 235–249.CrossRefGoogle Scholar
Hecht, F. 2012 New development in FreeFem++. J. Numer. Math. 20 (3-4), 251–265.CrossRefGoogle Scholar
Karniadakis, G. & Sherwin, S. 2005 Spectral/hp Element Methods for Computational Fluid Dynamics. Oxford University Press.CrossRefGoogle Scholar
Karniadakis, G. E. & Triantafyllou, G. S. 1989 Frequency selection and asymptotic states in laminar wakes. J. Fluid Mech. 199, 441–469.CrossRefGoogle Scholar
Kou, J., Zhanga, W., Liu, Y. & Li, X. 2017 The lowest Reynolds number of vortex-induced vibrations. Phys. Fluids 29, 041701.CrossRefGoogle Scholar
Leontini, J. S., Griffith, M. D., Lo Jacono, D. & Sheridan, J. 2018 The flow-induced vibration of an elliptical cross-section at varying angles of attack. J. Fluids Struct. 78, 356–373.CrossRefGoogle Scholar
Leontini, J. S., Stewart, B. E., Thompson, M. C. & Hourigan, K. 2006a Wake state and energy transitions of an oscillating cylinder at low Reynolds number. Phys. Fluids 18 (6), 067101.CrossRefGoogle Scholar
Leontini, J. S., Thompson, M. C. & Hourigan, K. 2006b The beginning of branching behaviour of vortex-induced vibration during two-dimensional flow. J. Fluids Struct. 22 (6–7), 857–864.CrossRefGoogle Scholar
Meliga, P. & Chomaz, J. M. 2011 An asymptotic expansion for the vortex-induced vibrations of a circular cylinder. J. Fluid Mech. 671, 137–167.CrossRefGoogle Scholar
Mittal, S. & Singh, S. 2005 Vortex-induced vibrations at subcritical Re. J. Fluid Mech. 534, 185–194.CrossRefGoogle Scholar
Morse, T. L. & Williamson, C. H. K. 2006 Employing controlled vibrations to predict fluid forces on a cylinder undergoing vortex-induced vibration. J. Fluids Struct. 22 (6), 877–884.CrossRefGoogle Scholar
Morse, T. L. & Williamson, C. H. K. 2009a Fluid forcing, wake modes, and transitions for a cylinder undergoing controlled oscillations. J. Fluids Struct. 25 (4), 697–712.CrossRefGoogle Scholar
Morse, T. L. & Williamson, C. H. K. 2009b Prediction of vortex-induced vibration response by employing controlled motion. J. Fluid Mech. 634, 5–39.CrossRefGoogle Scholar
Mougin, G. & Magnaudet, J. 2002 The generalized Kirchhoff equations and their application to the interaction between a rigid body and an arbitrary time-dependent viscous flow. Intl J. Multiphase Flow 28 (11), 1837–1851.CrossRefGoogle Scholar
Navrose & Mittal, S. 2016 Lock-in in vortex-induced vibration. J. Fluid Mech. 794, 565–594.CrossRefGoogle Scholar
Parkinson, G. 1989 Phenomena and modelling of flow-induced vibrations of bluff bodies. Prog. Aerosp. Sci. 26 (2), 169–224.CrossRefGoogle Scholar
Provansal, M., Mathis, C. & Boyer, L. 1987 Bénard–von Kármán instability: transient and forced regimes. J. Fluid Mech. 182, 1–22.CrossRefGoogle Scholar
Thompson, M. C., Hourigan, K. & Sheridan, J. 1996 Three-dimensional instabilities in the wake of a circular cylinder. J. Expl Therm. Fluid Sci. 12 (2), 190–196.CrossRefGoogle Scholar
Williamson, C. H. K. & Govardhan, R. 2004 Vortex-induced vibrations. Annu. Rev. Fluid Mech. 36, 413–455.CrossRefGoogle Scholar
Williamson, C. H. K. & Roshko, A. 1988 Vortex formation in the wake of an oscillating cylinder. J. Fluids Struct. 2 (4), 355–381.CrossRefGoogle Scholar
Zhang, W., Li, X., Ye, Z. & Jiang 2015 Mechanism of frequency lock-in in vortex-induced vibrations at low Reynolds numbers. J. Fluid Mech. 783, 72–102.CrossRefGoogle Scholar