Article contents
Vortex-dipole collapse induced by droplet inertia and phase change
Published online by Cambridge University Press: 26 October 2017
Abstract
Droplet-laden flows with phase change are common. This study brings to light a mechanism by which droplet inertial dynamics and local phase change, taking place at sub-Kolmogorov scales, affect vortex dynamics in the inertial range of turbulence. To do this we consider vortices placed in a supersaturated ambient initially at constant temperature, homogeneous vapour concentration and uniformly distributed droplets. The droplets also act as sites of phase change. This allows the time scales associated with particle inertia and phase change, which could be significantly different from each other and from the time scale of the flow, to become coupled, and for their combined dynamics to govern the flow. The thermodynamics of condensation and evaporation have a characteristic time scale 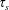 $\unicode[STIX]{x1D70F}_{s}$. The water droplets are treated as Stokesian inertial particles with a characteristic time scale
$\unicode[STIX]{x1D70F}_{s}$. The water droplets are treated as Stokesian inertial particles with a characteristic time scale 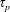 $\unicode[STIX]{x1D70F}_{p}$, whose behaviour we approximate using an
$\unicode[STIX]{x1D70F}_{p}$, whose behaviour we approximate using an 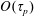 $O(\unicode[STIX]{x1D70F}_{p})$ truncation of the Maxey–Riley equation for heavy particles. This inertia leads the water droplets to vacate the vicinity of vortices, leaving no nuclei for the vapour to condense. The condensation process is thus spatially inhomogeneous, and leaves vortices in the flow colder than their surroundings. The combination of buoyancy and vorticity generates a lift force on the vortices perpendicular to their velocity relative to the fluid around them. In the case of a vortex dipole, this lift force can propel the vortices towards each other and undergo collapse, a phenomenon studied by Ravichandran et al. (Phys. Rev. Fluids, vol. 2, 2017, 034702). We find, spanning the space of the two time scales,
$O(\unicode[STIX]{x1D70F}_{p})$ truncation of the Maxey–Riley equation for heavy particles. This inertia leads the water droplets to vacate the vicinity of vortices, leaving no nuclei for the vapour to condense. The condensation process is thus spatially inhomogeneous, and leaves vortices in the flow colder than their surroundings. The combination of buoyancy and vorticity generates a lift force on the vortices perpendicular to their velocity relative to the fluid around them. In the case of a vortex dipole, this lift force can propel the vortices towards each other and undergo collapse, a phenomenon studied by Ravichandran et al. (Phys. Rev. Fluids, vol. 2, 2017, 034702). We find, spanning the space of the two time scales, 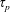 $\unicode[STIX]{x1D70F}_{p}$ and
$\unicode[STIX]{x1D70F}_{p}$ and 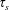 $\unicode[STIX]{x1D70F}_{s}$, the region in which lift-induced dipole collapse can occur, and show numerically that the product of the time scales is the determining parameter. Our findings agree with our results from scaling arguments. We also study the influence of varying the initial supersaturation, and find that the strength of the lift-induced mechanism has a power-law dependence on the phase-change time scale
$\unicode[STIX]{x1D70F}_{s}$, the region in which lift-induced dipole collapse can occur, and show numerically that the product of the time scales is the determining parameter. Our findings agree with our results from scaling arguments. We also study the influence of varying the initial supersaturation, and find that the strength of the lift-induced mechanism has a power-law dependence on the phase-change time scale 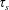 $\unicode[STIX]{x1D70F}_{s}$. We then study systems of many vortices and show that the same coupling between the two time scales alters the dynamics of such systems, by energising the smaller scales. We show that this effect is significantly more pronounced at higher Reynolds numbers. Finally, we discuss how this effect could be relevant in conditions typical of clouds.
$\unicode[STIX]{x1D70F}_{s}$. We then study systems of many vortices and show that the same coupling between the two time scales alters the dynamics of such systems, by energising the smaller scales. We show that this effect is significantly more pronounced at higher Reynolds numbers. Finally, we discuss how this effect could be relevant in conditions typical of clouds.
- Type
- Papers
- Information
- Copyright
- © 2017 Cambridge University Press
References
- 11
- Cited by



