Article contents
Unified theory for a sheared gas–solid suspension: from rapid granular suspension to its small-Stokes-number limit
Published online by Cambridge University Press: 15 May 2019
Abstract
A non-perturbative nonlinear theory for moderately dense gas–solid suspensions is outlined within the framework of the Boltzmann–Enskog equation by extending the work of Saha & Alam (J. Fluid Mech., vol. 833, 2017, pp. 206–246). A linear Stokes’ drag law is adopted for gas–particle interactions, and the viscous dissipation due to hydrodynamic interactions is incorporated in the second-moment equation via a density-corrected Stokes number. For the homogeneous shear flow, the present theory provides a unified treatment of dilute to dense suspensions of highly inelastic particles, encompassing the high-Stokes-number rapid granular regime (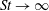 $St\rightarrow \infty$) and its small-Stokes-number counterpart, with quantitative agreement for all transport coefficients. It is shown that the predictions of the shear viscosity and normal-stress differences based on existing theories deteriorate markedly with increasing density as well as with decreasing Stokes number and restitution coefficient.
$St\rightarrow \infty$) and its small-Stokes-number counterpart, with quantitative agreement for all transport coefficients. It is shown that the predictions of the shear viscosity and normal-stress differences based on existing theories deteriorate markedly with increasing density as well as with decreasing Stokes number and restitution coefficient.
- Type
- JFM Papers
- Information
- Copyright
- © 2019 Cambridge University Press
References
- 10
- Cited by


