Article contents
Unconfined turbulent entrainment across density interfaces
Published online by Cambridge University Press: 23 September 2014
Abstract
We present theoretical models describing the quasi-steady downward transport of buoyant fluid across a gravitationally stable density interface separating two unbounded quiescent fluid masses. The primary transport mechanism is turbulent entrainment resulting from the localised impingement of a vertically forced high-Reynolds-number axisymmetric jet with steady source conditions. The entrainment across the interface is examined in the large-time asymptotic state, wherein the interfacial gravity current, formed by the fluid entrained from the upper layer and the jet, becomes infinitesimally thin and a two-layer stratification persists. Characterising flows with small interfacial Froude numbers 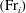 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}({{\mathrm{Fr}}}_i)$ as an axisymmetric semi-ellipsoidal impingement dome, we combine conservation equations with a mechanistic model of entrainment and reveal that, in this regime, the dimensionless entrainment flux
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}({{\mathrm{Fr}}}_i)$ as an axisymmetric semi-ellipsoidal impingement dome, we combine conservation equations with a mechanistic model of entrainment and reveal that, in this regime, the dimensionless entrainment flux 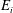 $E_i$ across the interface follows the power law
$E_i$ across the interface follows the power law 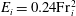 $E_i = 0.24{{\mathrm{Fr}}}_i^2$. For large-
$E_i = 0.24{{\mathrm{Fr}}}_i^2$. For large-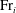 ${{\mathrm{Fr}}}_i$ impingements, modelled as a fully penetrating turbulent fountain, we show that
${{\mathrm{Fr}}}_i$ impingements, modelled as a fully penetrating turbulent fountain, we show that 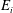 $E_i$ no longer scales with
$E_i$ no longer scales with 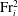 ${{\mathrm{Fr}}}_i^2$, but linearly on
${{\mathrm{Fr}}}_i^2$, but linearly on 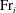 ${{\mathrm{Fr}}}_i$, following
${{\mathrm{Fr}}}_i$, following 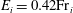 $E_i = 0.42{{\mathrm{Fr}}}_i$. We establish the intermediate range of
$E_i = 0.42{{\mathrm{Fr}}}_i$. We establish the intermediate range of 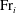 ${{\mathrm{Fr}}}_i$ over which there is a transition between these quadratic and linear power laws, thus enabling us to classify the dynamics of entrainment across the interface into three distinct regimes. Finally, the close agreement of our solutions with existing experimental results is illustrated.
${{\mathrm{Fr}}}_i$ over which there is a transition between these quadratic and linear power laws, thus enabling us to classify the dynamics of entrainment across the interface into three distinct regimes. Finally, the close agreement of our solutions with existing experimental results is illustrated.
- Type
- Papers
- Information
- Copyright
- © 2014 Cambridge University Press
References
- 20
- Cited by


