Article contents
Turbulent drag reduction by compliant lubricating layer
Published online by Cambridge University Press: 24 January 2019
Abstract
We propose a physically sound explanation for the drag reduction mechanism in a lubricated channel, a flow configuration in which an interface separates a thin layer of less-viscous fluid (viscosity 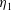 $\unicode[STIX]{x1D702}_{1}$) from a main layer of a more-viscous fluid (viscosity
$\unicode[STIX]{x1D702}_{1}$) from a main layer of a more-viscous fluid (viscosity 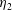 $\unicode[STIX]{x1D702}_{2}$). To single out the effect of surface tension, we focus initially on two fluids having the same density and the same viscosity (
$\unicode[STIX]{x1D702}_{2}$). To single out the effect of surface tension, we focus initially on two fluids having the same density and the same viscosity (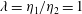 $\unicode[STIX]{x1D706}=\unicode[STIX]{x1D702}_{1}/\unicode[STIX]{x1D702}_{2}=1$), and we lower the viscosity of the lubricating layer down to
$\unicode[STIX]{x1D706}=\unicode[STIX]{x1D702}_{1}/\unicode[STIX]{x1D702}_{2}=1$), and we lower the viscosity of the lubricating layer down to 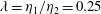 $\unicode[STIX]{x1D706}=\unicode[STIX]{x1D702}_{1}/\unicode[STIX]{x1D702}_{2}=0.25$, which corresponds to a physically realizable experimental set-up consisting of light oil and water. A database comprising original direct numerical simulations of two-phase flow channel turbulence is used to study the physical mechanisms driving drag reduction, which we report between 20 and 30 percent. The maximum drag reduction occurs when the two fluids have the same viscosity (
$\unicode[STIX]{x1D706}=\unicode[STIX]{x1D702}_{1}/\unicode[STIX]{x1D702}_{2}=0.25$, which corresponds to a physically realizable experimental set-up consisting of light oil and water. A database comprising original direct numerical simulations of two-phase flow channel turbulence is used to study the physical mechanisms driving drag reduction, which we report between 20 and 30 percent. The maximum drag reduction occurs when the two fluids have the same viscosity (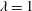 $\unicode[STIX]{x1D706}=1$), and corresponds to the relaminarization of the lubricating layer. Decreasing the viscosity of the lubricating layer (
$\unicode[STIX]{x1D706}=1$), and corresponds to the relaminarization of the lubricating layer. Decreasing the viscosity of the lubricating layer (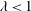 $\unicode[STIX]{x1D706}<1$) induces a marginally decreased drag reduction, but also helps sustaining strong turbulence in the lubricating layer. This led us to infer two different mechanisms for the two drag-reduced systems, each of which is ultimately controlled by the outcome of the competition between viscous, inertial and surface tension forces.
$\unicode[STIX]{x1D706}<1$) induces a marginally decreased drag reduction, but also helps sustaining strong turbulence in the lubricating layer. This led us to infer two different mechanisms for the two drag-reduced systems, each of which is ultimately controlled by the outcome of the competition between viscous, inertial and surface tension forces.
JFM classification
- Type
- JFM Rapids
- Information
- Copyright
- © 2019 Cambridge University Press
References
- 17
- Cited by


