Hostname: page-component-76fb5796d-dfsvx Total loading time: 0 Render date: 2024-04-26T01:40:26.493Z Has data issue: false hasContentIssue false
  • English
  • Français

Transport and instability in driven two-dimensional magnetohydrodynamic flows

Published online by Cambridge University Press:  28 June 2016

Sam Durston  and
Andrew D. Gilbert
Sam Durston
Affiliation:
Department of Mathematics and Computer Science, College of Engineering, Mathematics and Physical Sciences, University of Exeter, EX4 4QF, UK
Andrew D. Gilbert*
Affiliation:
Department of Mathematics and Computer Science, College of Engineering, Mathematics and Physical Sciences, University of Exeter, EX4 4QF, UK
*
†Email address for correspondence: A.D.Gilbert@exeter.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper concerns the generation of large-scale flows in forced two-dimensional systems. A Kolmogorov flow with a sinusoidal profile in one direction (driven by a body force) is known to become unstable to a large-scale flow in the perpendicular direction at a critical Reynolds number. This can occur in the presence of a 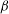${\it\beta}$-effect and has important implications for flows observed in geophysical and astrophysical systems. It has recently been termed ‘zonostrophic instability’ and studied in a variety of settings, both numerically and analytically. The goal of the present paper is to determine the effect of magnetic field on such instabilities using the quasi-linear approximation, in which the full fluid system is decoupled into a mean flow and waves of one scale. The waves are driven externally by a given random body force and move on a fast time scale, while their stress on the mean flow causes this to evolve on a slow time scale. Spatial scale separation between waves and mean flow is also assumed, to allow analytical progress. The paper first discusses purely hydrodynamic transport of vorticity including zonostrophic instability, the effect of uniform background shear and calculation of equilibrium profiles in which the effective viscosity varies spatially, through the mean flow. After brief consideration of passive scalar transport or equivalently kinematic magnetic field evolution, the paper then proceeds to study the full magnetohydrodynamic system and to determine effective diffusivities and other transport coefficients using a mixture of analytical and numerical methods. This leads to results on the effect of magnetic field, background shear and ${\it\beta}$-effect on zonostrophic instability and magnetically driven instabilities.

JFM classification

Instability: Instability MHD and Electrohydrodynamics: MHD and Electrohydrodynamics
Type
Papers
Information
Journal of Fluid Mechanics , Volume 799 , 25 July 2016 , pp. 541 - 578
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aubert, J. 2005 Steady zonal flows in spherical shell dynamos. J. Fluid Mech. 542, 53–67.Google Scholar
Bajer, K., Bassom, A. P. & Gilbert, A. D. 2001 Accelerated diffusion in the centre of a vortex. J. Fluid Mech. 437, 395–411.Google Scholar
Bakas, N. A. & Iouannou, P. J. 2011 Structural stability theory of two-dimensional fluid flow under stochastic forcing. J. Fluid Mech. 682, 332–361.Google Scholar
Bakas, N. A. & Iouannou, P. J. 2013 On the mechanism underlying the spontaneous emergence of barotropic zonal jets. J. Atmos. Sci. 70, 2251–2271.Google Scholar
Bakas, N. A. & Iouannou, P. J. 2014 A theory for the emergence of coherent structures in beta-plane turbulence. J. Fluid Mech. 740, 312–341.Google Scholar
Bedrossian, J. & Masmoudi, N. 2015 Inviscid damping and the asymptotic stability of planar shear flows in the 2D Euler equations. In Publications Mathématiques de l’IHÉS, pp. 1–106. Springer.Google Scholar
Berloff, P., Kamenkovich, I. & Pedlosky, J. 2009 A mechanism of multiple zonal jets in the oceans. J. Fluid Mech. 628, 395–425.Google Scholar
Bernoff, A. J. & Lingevitch, J. F. 1994 Rapid relaxation of an axisymmetric vortex. Phys. Fluids 6, 3717–3723.Google Scholar
Bouchet, F. & Morita, H. 2010 Large time behavior and asymptotic stability of the 2D Euler and linearized Euler equations. Physica D 239, 948–966.Google Scholar
Bouchet, F., Nardini, C. & Tangarife, T. 2013 Kinetic theory of jet dynamics in the stochastic barotropic and 2d Navier–Stokes equations. J. Stat. Phys. 153, 572–625.Google Scholar
Bouchet, F., Nardini, C. & Tangarife, T. 2014 Stochastic averaging, large deviations and random transitions for the dynamics of 2D and geostrophic turbulent vortices. Fluid. Dyn. Res. 46, 061416.Google Scholar
Chechkin, A. V. 1999 Negative magnetic viscosity in two dimensions. J. Expl Theor. Phys. 89, 677–688.Google Scholar
Constantinou, N. C., Farrell, B. F. & Iouannou, P. J. 2014 Emergence and equilibration of jets in beta-plane turbulence: applications of stochastic structural stability theory. J. Atmos. Sci. 71, 1818–1842.CrossRefGoogle Scholar
Diamond, P. H., Itoh, S.-I., Itoh, K. & Silvers, L. J. 2007 Beta-plane MHD turbulence and dissipation in the solar tachocline. In The Solar Tachocline (ed. Hughes, D. W., Rosner, R. & Weiss, N. O.), pp. 213–239. Cambridge University Press.Google Scholar
Dritschel, D. G. & McIntyre, M. E. 2008 Multiple jets as PV staircases: the Phillips effect and the resilience of eddy-transport barriers. J. Atmos. Sci. 65, 855–874.Google Scholar
Dritschel, D. G. & Scott, R. K. 2011 Jet sharpening by turbulent mixing. Proc. R. Soc. Lond. A 369, 754–770.Google ScholarPubMed
Dunkerton, T. J. & Scott, R. K. 2008 A barotropic model of the angular momentum conserving potential vorticity staircase in spherical geometry. J. Atmos. Sci. 65, 1105–1135.Google Scholar
Durston, S.2015 Zonal jets and shear: transport properties of two-dimensional fluid flows. PhD thesis, University of Exeter, UK.Google Scholar
Farrell, B. F. & Iouannou, P. J. 2003 Structural stability of turbulent jets. J. Atmos. Sci. 60, 2101–2118.Google Scholar
Farrell, B. F. & Iouannou, P. J. 2006 Structure and spacing of jets in barotropic turbulence. J. Atmos. Sci. 64, 3652–3665.Google Scholar
Farrell, B. F. & Iouannou, P. J. 2008 Formation of jets by baroclinic turbulence. J. Atmos. Sci. 65, 3353–3375.Google Scholar
Frisch, U., Legras, B. & Villone, B. 1996 Large-scale Kolmogorov flow on the beta-plane and resonant wave interactions. Physica D 94, 36–56.Google Scholar
Galperin, B., Sukoriansky, S., Dikovskaya, N., Read, P. L., Yamazaki, Y. H. & Wordsworth, R. 2006 Anisotropic turbulence and zonal jets in rotating flows with a 𝛽 effect. Nonlinear Process. Geophys. 13, 83–98.Google Scholar
Galperin, B., Young, R. M. B., Sukoriansky, S., Dikovskaya, N., Read, P. L., Lancaster, A. J. & Armstrong, D. 2014 Cassini observations reveal a regime of zonostrophic macroturbulence on Jupiter. Icarus 229, 295–320.Google Scholar
Heimpel, M. A., Aurnou, J. & Wicht, J. 2005 Simulation of equatorial and high-latitude jets on Jupiter in a deep convection model. Nature 438, 193–196.Google Scholar
Hsu, P.-C. & Diamond, P. H. 2015 Zonal flow formation in the presence of ambient mean shear. Phys. Plasmas 22, 022306.Google Scholar
Hughes, D. W., Rosner, R. & Weiss, N. O. 2007 The Solar Tachocline. Cambridge University Press.Google Scholar
Keating, S. R. & Diamond, P. H. 2008 Turbulent resistivity in wavy two-dimensional magnetohydrodynamic turbulence. J. Fluid Mech. 595, 173–202.Google Scholar
Kim, E.-J. 2007 The role of magnetic shear in flow shear suppression. Phys. Plasmas 18, 084504.Google Scholar
Kim, E.-J. & MacGregor, K. B. 2003 Gravity wave driven flows in the solar tachocline. II: stationary flows. Astrophys. J. 588, 645–654.Google Scholar
Leprovost, N. & Kim, E.-J. 2008a Analytical theory of forced rotating sheared turbulence: the perpendicular case. Phys. Rev. E 78, 016301.Google Scholar
Leprovost, N. & Kim, E.-J. 2008b Analytical theory of forced rotating sheared turbulence: the parallel case. Phys. Rev. E 78, 036319.Google Scholar
Leprovost, N. & Kim, E.-J. 2009 Turbulent transport and dynamo in sheared MHD turbulence with a non-uniform magnetic field. Phys. Rev. E 80, 026302.Google Scholar
Manfroi, A. J. & Young, W. R. 1998 Slow evolution of zonal jets on the beta plane. J. Atmos. Sci. 56, 784–800.Google Scholar
Manfroi, A. J. & Young, W. R. 2002 Stability of 𝛽-plane Kolmogorov flow. Physica D 162, 208–232.Google Scholar
Meshalkin, L. D. & Sinai, I. G. 1961 Investigation of the stability of a stationary solution of a system of equations for the plane movement of an incompressible viscous fluid. Appl. Math. Mech. 25, 1700–1705.Google Scholar
Morin, V. & Dormy, E. 2004 Time dependent 𝛽-convection in rapidly rotating spherical shells. Phys. Fluids 16, 1603–1609.Google Scholar
Newton, A., Kim, E.-J. & Liu, H.-L. 2013 On the self-organizing process of large scale shear flows. Phys. Plasmas 20, 092306.Google Scholar
Olver, F. J. W., Lozier, D. W., Boisvert, R. F. & Clark, C. W. 2010 NIST Handbook of Mathematical Functions. Cambridge University Press.Google Scholar
Parker, J. B. & Krommes, J. A. 2013 Zonal flow as pattern formation. Phys. Plasmas 20, 100703.Google Scholar
Parker, J. B. & Krommes, J. A. 2014 Generation of zonal flows through symmetry breaking of statistical homogeneity. New J. Phys. 16, 035006.Google Scholar
Read, P. L., Jacoby, T. N. L., Rogberg, P. H. T., Wordsworth, R. D., Yamazaki, Y. H., Miki-Yamazaki, K., Young, R. M. B., Sommeria, J., Didelle, H. & Viboud, S. 2015 An experimental study of multiple zonal jet formation in rotating, thermally driven convective flows on a topographic beta-plane. Phys. Fluids 27, 085111.Google Scholar
Read, P. L., Yamazaki, Y. H., Lewis, S. R., Williams, P. D., Wordsworth, R., Miki-Yamazaki, K., Sommeria, J., Didelle, H. & Fincham, A. M. 2007 Dynamics of convectively driven banded jets in the laboratory. J. Atmos. Sci. 64, 4031–4052.Google Scholar
Rhines, P. B. 1975 Waves and turbulence on the beta-plane. J. Fluid Mech. 69, 417–441.Google Scholar
Rotvig, J. & Jones, C. A. 2006 Multiple jets and bursting in the rapidly rotating convecting two-dimensional annulus model with nearly plane-parallel boundaries. J. Fluid Mech. 567, 117–140.Google Scholar
Scott, R. K. & Dritschel, D. G. 2012 The structure of zonal jets in geostrophic turbulence. J. Fluid Mech. 711, 576–598.Google Scholar
Scott, R. K. & Polvani, L. M. 2007 Forced-dissipative shalllow-water turbulence on the sphere and the atmospheric circulation of the giant planets. J. Atmos. Sci. 64, 3158–3176.Google Scholar
Srinivasan, K. & Young, W. R. 2012 Zonostrophic instability. J. Atmos. Sci. 69, 1633–1656.Google Scholar
Srinivasan, K. & Young, W. R. 2014 Reynolds stress and eddy diffusivity of 𝛽-plane shear flows. J. Atmos. Sci. 71, 2169–2185.Google Scholar
Sukoriansky, S., Galperin, B. & Chekhlov, A. 1999 Large scale drag representation in simulations of two-dimensional turbulence. Phys. Fluids 11, 3043–3053.Google Scholar
Tobias, S. M., Dagon, K. & Marston, J. B. 2011 Astrophysical fluid dynamics via direct statistical simulation. Astrophys. J. 727, 127.Google Scholar
Tobias, S. M., Hughes, D. W. & Diamond, P. H. 2007 𝛽-plane magnetohydrodynamic turbulence in the solar tachocline. Astrophys. J. 667, L113–116.Google Scholar
Vallis, G. K. & Maltrud, M. E. 1993 Generation of mean flow and jets on a beta plane and over topography. J. Phys. Oceanogr. 23, 1346–1362.Google Scholar
Weiss, N. O. 1966 The expulsion of magnetic flux by eddies. Proc. R. Soc. Lond. A 293, 310–328.Google Scholar
Yadav, R. K., Gastine, T., Christensen, U. R. & Reiners, A. 2015 Formation of starspots in self-consistent global dynamo models: polar spots on cool stars. Astron. Astrophys. 573, A68.Google Scholar
Zhang, K. & Jones, C. A. 1997 The effect of hyperviscosity on geodynamo models. Geophys. Res. Lett. 24, 2869–2872.Google Scholar
Zheligovksy, V. 2011 Large-Scale Perturbations of Magnetohydrodynamic Regimes: Linear and Weakly Nonlinear Stability Theory. Springer.Google Scholar