Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-24T12:32:03.727Z Has data issue: false hasContentIssue false
  • English
  • Français

Transition to the ultimate regime in a radiatively driven convection experiment

Published online by Cambridge University Press:  04 January 2019

Vincent Bouillaut ,
Simon Lepot ,
Sébastien Aumaître  and
Basile Gallet Open the ORCID record for Basile Gallet [Opens in a new window]
Vincent Bouillaut
Affiliation:
Service de Physique de l’État Condensé, CEA, CNRS UMR 3680, Université Paris-Saclay, CEA Saclay, 91191 Gif-sur-Yvette, France
Simon Lepot
Affiliation:
Service de Physique de l’État Condensé, CEA, CNRS UMR 3680, Université Paris-Saclay, CEA Saclay, 91191 Gif-sur-Yvette, France
Sébastien Aumaître
Affiliation:
Service de Physique de l’État Condensé, CEA, CNRS UMR 3680, Université Paris-Saclay, CEA Saclay, 91191 Gif-sur-Yvette, France
Basile Gallet*
Affiliation:
Service de Physique de l’État Condensé, CEA, CNRS UMR 3680, Université Paris-Saclay, CEA Saclay, 91191 Gif-sur-Yvette, France
*
†Email address for correspondence: basile.gallet@cea.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

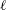We report on the transition between two regimes of heat transport in a radiatively driven convection experiment, where a fluid gets heated up within a tunable heating length $\ell$ in the vicinity of the bottom of the tank. The first regime is similar to that observed in standard Rayleigh–Bénard experiments, the Nusselt number 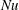$Nu$ being related to the Rayleigh number 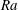$Ra$ through the power law 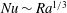$Nu\sim Ra^{1/3}$. The second regime corresponds to the ‘ultimate’ or mixing-length scaling regime of thermal convection, where 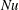$Nu$ varies as the square root of 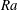$Ra$. Evidence for these two scaling regimes has been reported in Lepot et al. (Proc. Natl Acad. Sci. USA, vol. 115, 2018, pp. 8937–8941), and we now study in detail how the system transitions from one to the other. We propose a simple model describing radiatively driven convection in the mixing-length regime. It leads to the scaling relation 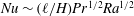$Nu\sim (\ell /H)Pr^{1/2}Ra^{1/2}$, where 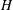$H$ is the height of the cell and 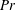$Pr$ is the Prandtl number, thereby allowing us to deduce the values of 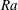$Ra$ and 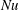$Nu$ at which the system transitions from one regime to the other. These predictions are confirmed by the experimental data gathered at various 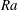$Ra$ and 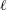$\ell$. We conclude by showing that boundary layer corrections can persistently modify the Prandtl number dependence of 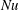$Nu$ at large 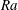$Ra$, for 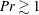$Pr\gtrsim 1$.

JFM classification

Turbulent Flows: Turbulent convection
Type
JFM Rapids
Information
Journal of Fluid Mechanics , Volume 861 , 25 February 2019 , R5
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alhers, G., Grossmann, S. & Lhose, D. 2009 Heat transfer and large-scale dynamics in turbulent Rayleigh–Bénard convection. Rev. Mod. Phys. 81, 503.Google Scholar
Aubert, J., Labrosse, S. & Poitou, C. 2009 Modelling the Palaeo-evolution of the geodynamo. Geophys. J. Intl 179, 1414–1428.Google Scholar
Barker, A. J., Dempsey, A. M. & Lithwick, Y. 2014 Theory and simulations of rotating convection. Astrophys. J. 791, 13.Google Scholar
Bengtsson, L. 1996 Mixing in ice-covered lakes. Hydrobiologia 322, 91–97.Google Scholar
Chavanne, X., Chillá, F., Castaing, B., Hébral, B., Chabaud, B. & Chaussy, J. 1997 Observation of the ultimate regime in Rayleigh–Bénard convection. Phys. Rev. Lett. 79, 3648.Google Scholar
Chavanne, X., Chillá, F., Chabaud, B., Castaing, B. & Hébral, B. 2001 Turbulent Rayleigh–Bénard convection in gaseous and liquid He. Phys. Fluids 13, 1300.Google Scholar
Davaille, A., Girard, F. & Le Bars, M. 2002 How to anchor hotspots in a convecting mantle? Earth Planet. Sci. Lett. 203, 621–634.Google Scholar
Farmer, D. 1975 Penetrative convection in the absence of mean shear. Q. J. R. Meteorol. Soc. 101, 869–891.Google Scholar
Goluskin, D. 2015 Internally heated convection beneath a poor conductor. J. Fluid Mech. 771, 36–56.Google Scholar
Goluskin, D. 2016 Internally Heated Convection and Rayleigh–Bénard Convection. Springer.Google Scholar
Gubbins, D., Alfé, D., Masters, G., David Price, G. & Gillan, M. J. 2003 Can the Earth’s dynamo run on heat alone? Geophys. J. Intl. 155, 609–622.Google Scholar
Herant, M., Benz, W. & Colgate, S. 1992 Postcollapse hydrodynamics of SN 1987A: two-dimensional simulations of the early evolution. Astrophys. J. 395, 642–653.Google Scholar
Janka, H.-T. & Müller, E. 1996 Neutrino heating, convection, and the mechanism of type-II supernova explosion. Astron. Astrophys. 306, 167.Google Scholar
Jonas, T., Terzhevik, A. Y., Mironov, D. V. & Wüest, A. 2003 Radiatively driven convection in an ice-covered lake investigated using temperature microstructure technique. J. Geophys. Res. 108, 3183.Google Scholar
Kazeroni, R., Krueger, B. K., Guilet, J., Foglizzo, T. & Pomaréde, D. 2016 The non-linear onset of neutrino-driven convection in two- and three-dimensional core-collapse supernovae. Mon. Not. R. Astron. Soc. 480, 261–280.Google Scholar
Kippenhahn, R. & Weigert, A. 1990 Stellar Structure and Evolution. Springer.Google Scholar
Kraichnan, R. H. 1962 Turbulent thermal convection at arbitrary Prandtl number. Phys. Fluids 5, 1374.Google Scholar
Kulacki, F. A. & Goldstein, R. J. 1972 Thermal convection in a horizontal fluid layer with uniform volumetric energy sources. J. Fluid Mech. 55, 271–287.Google Scholar
Landeau, M. & Aubert, J. 2011 Equatorially asymmetric convection inducing a hemispherical magnetic field in rotating spheres and implications for the past Martian dynamo. Phys. Earth Planet. Inter. 185, 61–74.Google Scholar
Lecoanet, D., Le Bars, M., Burns, K. J., Vasil, G. M., Brown, B. P., Quataert, E. & Oishi, J. S. 2015 Numerical simulations of internal wave generation by convection in water. Phys. Rev. E 91, 063016.Google Scholar
Lepot, S., Aumaître, S. & Gallet, B. 2018 Radiative heating achieves the ultimate regime of thermal convection. Proc. Natl Acad. Sci. USA 115, 8937–8941.Google Scholar
Limare, A., Vilella, K., Di Giuseppe, E., Farnetani, C. G., Kaminski, E., Surducan, E., Surducan, V., Neamtu, C., Fourel, L. & Jaupart, C. 2015 Microwave-heating laboratory experiments for planetary mantle convection. J. Fluid Mech. 777, 50–67.Google Scholar
Malkus, W. V. R. 1954 The heat transport and spectrum of thermal turbulence. Proc. R. Soc. Lond. A 225, 196–212.Google Scholar
Mironov, D., Terzhevik, A., Kirillin, G., Jonas, T., Malm, J. & Farmer, D. 2002 Radiatively driven convection in ice-covered lakes: observations, scaling, and a mixed-layer model. J. Geophys. Res. 107, 2001JC000892.Google Scholar
Niemela, J. J., Skrbek, L., Sreenivasan, K. R. & Donnelly, R. J. 2000 Turbulent convection at very high Rayleigh numbers. Nature 404, 837–840.Google Scholar
Radice, D., Ott, C. D., Abdikamalov, E., Couch, S. M., Haas, R. & Schnetter, E. 2016 Neutrino-driven convection in core-collapse supernovae: high-resolution simulations. Astrophys. J. 820, 76.Google Scholar
Roche, P.-E., Gauthier, F., Kaiser, R. & Salort, J. 2010 On the triggering of the ultimate regime of convection. New. J. Phys. 12, 085014.Google Scholar
Rusaouën, E., Liot, O., Castaing, B., Salort, J. & Chillá, F. 2018 Thermal transfer in Rayleigh–Bénard cell with smooth or rough boundaries. J. Fluid Mech. 837, 443–460.Google Scholar
Shen, Y., Tong, P. & Xia, K.-Q. 1996 Turbulent convection over rough surfaces. Phys. Rev. Lett. 76, 908.Google Scholar
Shraiman, B. I. & Siggia, E. D. 1990 Heat transport in high-Rayleigh-number convection. Phys. Rev. A 42, 3650(R).Google Scholar
Spiegel, E. A. 1963 A generalization of the mixing-length theory of thermal convection. Astrophys. J. 138, 216–225.Google Scholar
Spiegel, E. A. 1971 Convection in stars I. Basic Boussinesq convection. Annu. Rev. Astron. Astrophys. 9, 323–352.Google Scholar
Toppaladoddi, S., Succi, S. & Wettlaufer, J. S. 2017 Roughness as a route to the ultimate regime of thermal convection. Phys. Rev. Lett. 118, 074503.Google Scholar
Toppaladoddi, S. & Wettlaufer, J. S. 2018 Penetrative convection at high Rayleigh numbers. Phys. Rev. Fluids 3, 043501.Google Scholar
Ulloa, H. N., Wüest, A. & Bouffard, D. 2018 Mechanical energy budget and mixing efficiency for a radiatively heated ice-covered waterbody. J. Fluid Mech. 852, R1.Google Scholar
Xie, Y.-C. & Xia, K.-Q. 2017 Turbulent thermal convection over rough plates with varying roughness geometry. J. Fluid Mech. 825, 573–599.Google Scholar