Hostname: page-component-7bb8b95d7b-cx56b Total loading time: 0 Render date: 2024-09-21T16:07:30.059Z Has data issue: false hasContentIssue false
  • English
  • Français

Transition to the secondary vortex street in the wake of a circular cylinder

Published online by Cambridge University Press:  27 March 2019

Hongyi Jiang Open the ORCID record for Hongyi Jiang [Opens in a new window]  and
Liang Cheng
Hongyi Jiang
Affiliation:
School of Engineering, The University of Western Australia, 35 Stirling Highway, Crawley, WA 6009, Australia
Liang Cheng*
Affiliation:
School of Engineering, The University of Western Australia, 35 Stirling Highway, Crawley, WA 6009, Australia State Key Laboratory of Coastal and Offshore Engineering, Dalian University of Technology, Dalian, 116024, PR China
*
†Email address for correspondence: liang.cheng@uwa.edu.au
Get access Rights & Permissions [Opens in a new window]

Abstract

Instabilities and flow characteristics in the far wake of a circular cylinder are examined through direct numerical simulations. The transitions to the two-layered and secondary vortex streets are quantified by a new method based on the time-averaged transverse velocity field. 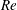Two processes for the transition to the secondary vortex street are observed: (i) the merging of two same-sign vortices over a range of low Reynolds numbers ($Re$) between 200 and 300, and (ii) the pairing of two opposite-sign vortices, followed by the merging of the paired vortices into subsequent vortices, over a range of 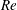$Re$ between 400 and 1000. Single vortices may be generated between the merging cycles due to mismatch of the vortices. The irregular merging process results in flow irregularity and an additional frequency signal 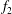$f_{2}$ (in addition to the primary vortex shedding frequency 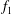$f_{1}$) in the two-layered and secondary vortex streets. In particular, a gradual energy transfer from 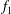$f_{1}$ to 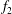$f_{2}$ with distance downstream is observed in the two-layered vortex street prior to the merging. The frequency spectra of 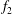$f_{2}$ are broad-band for 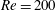$Re=200$–300 but become increasingly sharp-peaked with increasing 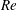$Re$ because the vortex merging process becomes increasingly regular. The ratio of the sharp-peaked frequencies 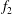$f_{2}$ and 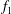$f_{1}$ is equal to the ratio of the numbers of vortices observed after and before the merging. The general conclusions drawn from a circular cylinder are expected to be applicable to other bluff bodies.

JFM classification

Vortex Flows: Vortex instability Wakes/Jets: Vortex streets Wakes/Jets: Wakes
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 867 , 25 May 2019 , pp. 691 - 722
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abdessemed, N., Sharma, A. S., Sherwin, S. J. & Theofilis, V. 2009 Transient growth analysis of the flow past a circular cylinder. Phys. Fluids 21, 044103.Google Scholar
Akbar, T., Bouchet, G. & Dušek, J. 2011 Numerical investigation of the subcritical effects at the onset of three-dimensionality in the circular cylinder wake. Phys. Fluids 23, 094103.Google Scholar
Cantwell, C. D. et al. 2015 Nektar++ : An open-source spectral/hp element framework. Comput. Phys. Commun. 192, 205–219.Google Scholar
Cimbala, J. M.1984 Large structure in the far wakes of two-dimensional bluff bodies. PhD thesis, California Institute of Technology.Google Scholar
Cimbala, J. M., Nagib, H. M. & Roshko, A. 1988 Large structure in the far wakes of two-dimensional bluff bodies. J. Fluid Mech. 190, 265–298.Google Scholar
Durgin, W. W. & Karlsson, S. K. F. 1971 On the phenomenon of vortex street breakdown. J. Fluid Mech. 48, 507–527.Google Scholar
Dynnikova, G. Y., Dynnikov, Y. A. & Guvernyuk, S. V. 2016 Mechanism underlying Kármán vortex street breakdown preceding secondary vortex street formation. Phys. Fluids 28, 054101.Google Scholar
Henderson, R. D. 1997 Nonlinear dynamics and pattern formation in turbulent wake transition. J. Fluid Mech. 352, 65–112.Google Scholar
Inoue, O. & Yamazaki, T. 1999 Secondary vortex streets in two-dimensional cylinder wakes. Fluid Dyn. Res. 25, 1–18.Google Scholar
Jiang, H. & Cheng, L. 2017 Strouhal–Reynolds number relationship for flow past a circular cylinder. J. Fluid Mech. 832, 170–188.Google Scholar
Jiang, H., Cheng, L., Draper, S., An, H. & Tong, F. 2016 Three-dimensional direct numerical simulation of wake transitions of a circular cylinder. J. Fluid Mech. 801, 353–391.Google Scholar
Karasudani, T. & Funakoshi, M. 1994 Evolution of a vortex street in the far wake of a cylinder. Fluid Dyn. Res. 14, 331–352.Google Scholar
Kumar, B. & Mittal, S. 2012 On the origin of the secondary vortex street. J. Fluid Mech. 711, 641–666.Google Scholar
Matsui, T. & Okude, M. 1983 Formation of the secondary vortex street in the wake of a circular cylinder. In Structure of Complex Turbulent Shear Flow (ed. Dumas, R. & Fulachier, L.), International Union of Theoretical and Applied Mechanics. Springer.Google Scholar
Osamu, I. & Yamazaki, T. 1999 Secondary vortex streets in two-dimensional cylinder wakes. Fluid Dyn. Res. 25, 1–18.Google Scholar
Posdziech, O. & Grundmann, R. 2001 Numerical simulation of the flow around an infinitely long circular cylinder in the transition regime. Theor. Comput. Fluid Dyn. 15, 121–141.Google Scholar
Taneda, S. 1959 Downstream development of the wakes behind cylinders. J. Phys. Soc. Japan 14, 843–848.Google Scholar
Thompson, M. C., Radi, A., Rao, A., Sheridan, J. & Hourigan, K. 2014 Low-Reynolds-number wakes of elliptical cylinders: from the circular cylinder to the normal flat plate. J. Fluid Mech. 751, 570–600.Google Scholar
Vorobieff, P., Georgiev, D. & Ingber, M. S. 2002 Onset of the second wake: dependence on the Reynolds number. Phys. Fluids 14, L53.Google Scholar
Wang, S., Tian, F., Jia, L., Lu, X. & Yin, X. 2010 Secondary vortex street in the wake of two tandem circular cylinders at low Reynolds number. Phys. Rev. E 81, 036305.Google Scholar
Williamson, C. H. K. 1996 Three-dimensional wake transition. J. Fluid Mech. 328, 345–407.Google Scholar
Williamson, C. H. K. & Prasad, A. 1993 A new mechanism for oblique wave resonance in the ‘natural’ far wake. J. Fluid Mech. 256, 269–313.Google Scholar

Jiang and Cheng supplementary movie 1

Time-evolution of the vorticity field for Re = 600.

Download Jiang and Cheng supplementary movie 1(Video)
Video 3.7 MB

Jiang and Cheng supplementary movie 2

Time-evolution of the vorticity field for Re = 300.

Download Jiang and Cheng supplementary movie 2(Video)
Video 3.7 MB